WikiDer > Сопротивление материалов

Strength of materials

Сопротивление материалов, также называемый механика материалов, имеет дело с поведением твердых объектов в зависимости от подчеркивает и напряжения. Полная теория началась с рассмотрения поведения одно- и двумерных элементов конструкций, чьи напряженные состояния могут быть аппроксимированы как двумерные, а затем была обобщена на трехмерные для разработки более полной теории упругого и пластического поведения конструкций. материалы. Важным пионером в области механики материалов был Стивен Тимошенко.

Изучение прочности материалов часто относится к различным методам расчета напряжений и деформаций в элементах конструкции, таких как балки, колонны и валы. Методы, используемые для прогнозирования реакции конструкции под нагрузкой и ее восприимчивости к различным режимам разрушения, учитывают свойства материалов, такие как предел текучести, невероятная сила, Модуль для младших, и Коэффициент Пуассона. Кроме того, учитываются макроскопические свойства механического элемента (геометрические свойства), такие как его длина, ширина, толщина, граничные ограничения и резкие изменения геометрии, такие как отверстия.

Определение

В механике материалов прочность материала - это его способность выдерживать приложенную нагрузку без разрушения или Пластическая деформация. Поле прочности материалов имеет дело с силами и деформациями, возникающими в результате их воздействия на материал. Нагрузка, приложенная к механическому элементу, будет вызывать внутренние силы внутри элемента, называемые напряжениями, когда эти силы выражаются в единицах. Напряжения, действующие на материал, вызывают различные деформации материала, включая их полное разрушение. Деформация материала называется деформацией, если и эти деформации относятся к единице.

Напряжения и деформации, возникающие в механическом элементе, необходимо рассчитать, чтобы оценить его несущую способность. Это требует полного описания геометрии элемента, его ограничений, нагрузок, приложенных к элементу, и свойств материала, из которого он состоит. Прилагаемые нагрузки могут быть осевыми (растягивающими или сжимающими) или вращательными (прочность на сдвиг). С полным описанием нагрузки и геометрической формы элемента можно рассчитать напряженное и деформированное состояние в любой точке элемента. После того, как состояние напряжения и деформации внутри элемента известно, можно рассчитать прочность (несущую способность) этого элемента, его деформации (характеристики жесткости) и его стабильность (способность сохранять свою первоначальную конфигурацию).

Рассчитанные напряжения затем можно сравнить с некоторой мерой прочности элемента, такой как текучесть материала или предел прочности. Рассчитанный прогиб элемента можно сравнить с критериями прогиба, основанными на использовании элемента. Расчетную нагрузку на продольный изгиб элемента можно сравнить с приложенной нагрузкой. Расчетная жесткость и распределение массы элемента могут использоваться для расчета динамического отклика элемента, а затем сравниваться с акустической средой, в которой он будет использоваться.

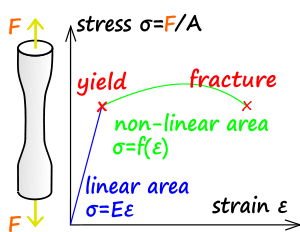
Прочность материала относится к инженерной кривая напряжение – деформация (предел текучести), за пределами которого материал испытывает деформации, которые не будут полностью устранены после снятия нагрузки, и в результате элемент будет иметь постоянный прогиб. Предел прочности материала означает максимальное достигаемое значение напряжения. Прочность на излом - это значение напряжения при разрушении (последнее зарегистрированное значение напряжения).

Виды нагрузок

  • Поперечные нагрузки - силы, приложенные перпендикулярно продольной оси элемента. Поперечная нагрузка заставляет элемент изгибаться и отклоняться от исходного положения с внутренними деформациями растяжения и сжатия, сопровождающими изменение кривизны элемента.[1] Поперечная нагрузка также вызывает силы сдвига, которые вызывают деформацию сдвига материала и увеличивают поперечный прогиб элемента.
  • Осевая нагрузка - приложенные силы коллинеарны продольной оси элемента. Силы заставляют элемент либо растягиваться, либо укорачиваться.[2]
  • Торсионная нагрузка - скручивающее действие, вызванное парой приложенных извне равных и противоположно направленных пар сил, действующих в параллельных плоскостях, или единственной внешней парой, приложенной к элементу, один конец которого зафиксирован против вращения.

Условия стресса

Материал нагружается а) сжатием, б) растяжением, в) сдвигом.

Одноосное напряжение выражается

куда F сила [Н], действующая на площадь А [м2].[3] Зона может быть недеформированной или деформированной, в зависимости от того, инженерное напряжение или настоящий стресс представляет интерес.

  • Сжимающее напряжение (или же сжатие) - это напряженное состояние, вызванное приложенной нагрузкой, уменьшающей длину материала (элемент сжатия) вдоль оси приложенной нагрузки, другими словами, это напряженное состояние, вызывающее сжатие материала. Простым случаем сжатия является одноосное сжатие, вызванное действием противоположных толкающих сил. Прочность на сжатие материалов обычно выше, чем их предел прочности на разрыв. Однако конструкции, нагруженные при сжатии, подвержены дополнительным режимам отказа, таким как коробление, которые зависят от геометрии элемента.
  • Растягивающее напряжение - это напряженное состояние, вызванное приложенной нагрузкой, которая стремится удлинить материал вдоль оси приложенной нагрузки, другими словами, напряжение, вызванное тянущий материал. Прочность конструкций одинаковой площади поперечного сечения, нагруженных на растяжение, не зависит от формы поперечного сечения. Материалы, нагруженные при растяжении, подвержены концентрации напряжений например, дефекты материала или резкие изменения геометрии. Однако материалы, демонстрирующие пластичные свойства (например, большинство металлов), могут допускать некоторые дефекты, в то время как хрупкие материалы (например, керамика) могут разрушаться при значительно меньшей прочности, чем их предел прочности.
  • Напряжение сдвига это напряженное состояние, вызванное объединенной энергией пары противоположных сил, действующих вдоль параллельных линий действия через материал, другими словами, напряжение, вызванное гранями материала. скольжение относительно друг друга. Пример - резка бумаги ножницы[4] или напряжения из-за крутильных нагрузок.

Параметры напряжения для сопротивления

Сопротивление материала можно выразить несколькими механическое напряжение параметры. Период, термин прочность материала используется при ссылке на механическое напряжение параметры. Это физические величины с размерами, однородными давление и сила на единицу поверхности. Поэтому традиционной единицей измерения силы является МПа в Международная система единиц, а psi между Обычные единицы СШАПараметры прочности включают: предел текучести, предел прочности, усталостную прочность, трещиностойкость и другие параметры.[нужна цитата]

  • Предел текучести это наименьшее напряжение, вызывающее необратимую деформацию материала. В некоторых материалах, например алюминиевые сплавы, точку текучести трудно определить, поэтому ее обычно определяют как напряжение, необходимое для возникновения 0,2% пластической деформации. Это называется пределом текучести 0,2%.[5]
  • Прочность на сжатие это предельное состояние сжимающее напряжение что приводит к разрушению материала в виде пластического разрушения (бесконечный теоретический предел текучести) или хрупкого разрушения (разрушения в результате распространения трещины или скольжения по слабой плоскости - см. прочность на сдвиг).
  • Предел прочности или же предел прочности на растяжение это предельное состояние растягивающее напряжение что приводит к разрушению при растяжении в виде пластичного разрушения (текучесть на первой стадии этого разрушения, некоторое упрочнение на второй стадии и разрушение после возможного образования шейки) или хрупкого разрушения (внезапное разрушение двух или более частей на низкое напряжение). Предел прочности при растяжении может быть указан как истинное напряжение или инженерное напряжение, но инженерное напряжение является наиболее часто используемым.
  • Предел выносливости - более сложная мера прочности материала, учитывающая несколько эпизодов нагружения в период эксплуатации объекта,[6] и обычно его труднее оценить, чем измерения статической прочности. Усталостная прочность здесь указана как простой классифицировать (). В случае циклическая загрузка это может быть соответствующим образом выражено как амплитуда обычно при нулевом среднем напряжении, а также количестве циклов до отказа в этом состоянии напряжения.
  • Сила удара - способность материала выдерживать внезапно приложенную нагрузку, выражаемая в единицах энергии. Часто измеряется Испытание на ударную вязкость по Изоду или же Испытание на удар по Шарпи, оба из которых измеряют энергию удара, необходимую для разрушения образца. Объем, модуль эластичность, распределение сил и предел текучести влияют на ударную вязкость материала. Чтобы материал или объект имел высокую ударную вязкость, напряжения должны распределяться равномерно по всему объекту. Он также должен иметь большой объем с низким модулем упругости и высоким пределом текучести материала.[7]

Параметры деформации для сопротивления

  • Деформация материала - это изменение геометрии, возникающее при приложении напряжения (в результате приложенных сил, гравитационных полей, ускорений, теплового расширения и т. д.). Деформация выражается полем смещения материала.[8]
  • Напряжение или же уменьшенная деформация - математический термин, который выражает тенденцию изменения деформации в поле материала. Деформация - это деформация на единицу длины.[9] В случае одноосного нагружения смещения образца (например, стержневого элемента) приводят к вычислению деформации, выражаемой как частное от смещения к исходной длине образца. Для трехмерных полей смещения он выражается как производные от функций смещения второго порядка тензор (с 6 независимыми элементами).
  • Прогиб - это термин, описывающий величину, до которой смещается элемент конструкции под действием приложенной нагрузки.[10]

Отношения напряжения и деформации

Основная статья: Кривая напряжение – деформация
Основной статический отклик образца при растяжении
  • Эластичность это способность материала возвращаться к своей прежней форме после снятия напряжения. Во многих материалах соотношение между приложенным напряжением прямо пропорционально результирующей деформации (до определенного предела), а график, представляющий эти две величины, представляет собой прямую линию.

Наклон этой линии известен как Модуль для младших, или «модуль упругости». Модуль упругости можно использовать для определения зависимости напряжение-деформация на линейно-упругой части кривой напряжения-деформации. Область линейно-упругой деформации либо ниже предела текучести, либо, если предел текучести не легко определить на графике напряжение-деформация, он определяется как деформация от 0 до 0,2% и определяется как область деформации, в которой нет податливость (остаточная деформация).[11]

  • Пластичность или пластическая деформация противоположна упругой деформации и определяется как невосстановимая деформация. Пластическая деформация сохраняется после снятия приложенного напряжения. Большинство материалов линейно-упругой категории обычно способны к пластической деформации. Хрупкие материалы, такие как керамика, не подвергаются пластической деформации и будут разрушаться при относительно низкой деформации, в то время как пластичные материалы, такие как металлы, свинец или полимеры, будут пластически деформироваться намного сильнее до начала разрушения.

Рассмотрим разницу между морковью и жевательной резинкой. Морковь очень мало растянется перед тем, как сломаться. Жеванная жевательная резинка, с другой стороны, будет сильно пластически деформироваться, прежде чем окончательно сломаться.

Условия оформления

Предел прочности - это атрибут, связанный с материалом, а не только с конкретным образцом, изготовленным из материала, и поэтому он выражается как сила на единицу площади поперечного сечения (Н / м2). Предел прочности - это максимальное напряжение, которое может выдержать материал, прежде чем он сломается или ослабнет.[12] Например, предел прочности на разрыв (UTS) стали AISI 1018 составляет 440 МПа. В имперских единицах единицей измерения напряжения является фунт-сила / дюйм² или фунт-сила на квадратный дюйм. Этот блок часто обозначается как psi. Сокращенно одна тысяча фунтов на квадратный дюйм ksi.

А коэффициент безопасности это критерии проектирования, которым должен соответствовать спроектированный компонент или конструкция. , где FS: запас прочности, R: приложенное напряжение и UTS: предельное напряжение (фунт / кв. дюйм или Н / м2)[13]

Запас прочности также иногда используется в качестве критерия проектирования. Определяется MS = отказоустойчивая нагрузка / (запас прочности × прогнозируемая нагрузка) - 1.

Например, для достижения коэффициента безопасности 4 допустимое напряжение в стальном элементе AISI 1018 можно рассчитать следующим образом: = 440/4 = 110 МПа, или = 110×106 Н / м2. Такие допустимые напряжения также известны как «расчетные напряжения» или «рабочие напряжения».

Расчетные напряжения, которые были определены из значений предела или предела текучести материалов, дают безопасные и надежные результаты только в случае статической нагрузки. Многие детали машин выходят из строя при воздействии нестационарных и постоянно изменяющихся нагрузок, даже если возникающие напряжения ниже предела текучести. Такие отказы называются усталостными. Разрушение происходит из-за трещины, которая кажется хрупкой с небольшими видимыми признаками податливости или без них. Однако, когда напряжение поддерживается ниже «усталостного напряжения» или «предельного напряжения выносливости», деталь будет выдерживать неопределенное время. Чисто реверсивное или циклическое напряжение - это напряжение, которое чередуется между равными положительными и отрицательными пиковыми напряжениями в течение каждого рабочего цикла. При чисто циклическом напряжении среднее напряжение равно нулю. Когда деталь подвергается циклическому напряжению, также известному как диапазон напряжений (Sr), было замечено, что отказ детали происходит после ряда реверсивных напряжений (N), даже если величина диапазона напряжений ниже предел текучести материала. Как правило, чем выше напряжение диапазона, тем меньше реверсий требуется для отказа.

Теории неудач

Существует четыре теории разрушения: теория максимального напряжения сдвига, теория максимального нормального напряжения, теория максимальной деформации, теория максимальной энергии деформации и теория максимальной энергии деформации. Из этих четырех теорий разрушения теория максимального нормального напряжения применима только к хрупким материалам, а остальные три теории применимы к пластичным материалам. Из последних трех теорий энергии искажения дает наиболее точные результаты в большинстве напряжений. условия. Теория энергии деформации требует значения Коэффициент Пуассона материала детали, который часто недоступен. Теория максимального напряжения сдвига консервативна. Для простых однонаправленных нормальных напряжений все теории эквивалентны, что означает, что все теории дадут одинаковый результат.

  • Теория максимального касательного напряжения - Эта теория постулирует, что разрушение произойдет, если величина максимального напряжения сдвига в детали превышает прочность материала на сдвиг, определенную в результате одноосных испытаний.
  • Теория максимального нормального напряжения - Эта теория постулирует, что разрушение произойдет, если максимальное нормальное напряжение в детали превышает предельное напряжение растяжения материала, определенное в результате одноосных испытаний. Эта теория имеет дело только с хрупкими материалами. Максимальное растягивающее напряжение должно быть меньше или равно предельному растягивающему напряжению, деленному на запас прочности. Величина максимального сжимающего напряжения должна быть меньше предельного сжимающего напряжения, деленного на запас прочности.
  • Теория максимальной энергии деформации - Эта теория постулирует, что разрушение произойдет, когда энергия деформации на единицу объема из-за приложенных напряжений в детали равна энергии деформации на единицу объема в пределе текучести при одноосном испытании.
  • Теория энергии максимального искажения - Эта теория также известна как теория энергии сдвига или теория фон Мизеса-Хенки. Эта теория постулирует, что отказ произойдет, когда энергия искажения на единицу объема из-за приложенных напряжений в детали равна энергии искажения на единицу объема в пределе текучести при одноосном испытании. Общую упругую энергию из-за деформации можно разделить на две части: одна часть вызывает изменение объема, а другая часть вызывает изменение формы. Энергия искажения - это количество энергии, необходимое для изменения формы.
  • Механика разрушения была установлена Алан Арнольд Гриффит и Джордж Рэнкин Ирвин. Эта важная теория также известна как численное преобразование вязкости материала в случае наличия трещины.

Прочность материала зависит от его микроструктура. Технологические процессы, которым подвергается материал, могут изменить эту микроструктуру. Разнообразие механизмы укрепления которые изменяют прочность материала, включают упрочнение, упрочнение твердого раствора, осадочное твердение, и усиление границ зерен и может быть объяснен количественно и качественно. Механизмы упрочнения сопровождаются предупреждением о том, что некоторые другие механические свойства материала могут ухудшиться в попытке сделать материал более прочным. Например, при упрочнении границ зерен, хотя предел текучести увеличивается до максимума с уменьшением размера зерна, в конечном итоге очень маленькие размеры зерна делают материал хрупким. Как правило, предел текучести материала является адекватным показателем механической прочности материала. Рассматривается в тандеме с тем фактом, что предел текучести является параметром, который предсказывает Пластическая деформация в материале можно принимать обоснованные решения о том, как повысить прочность материала в зависимости от его микроструктурных свойств и желаемого конечного эффекта. Прочность выражается через предельные значения сжимающее напряжение, растягивающее напряжение, и напряжения сдвига это приведет к отказу. Эффекты динамического нагружения, вероятно, являются наиболее важным практическим рассмотрением прочности материалов, особенно проблемой усталость. Часто возникает повторная загрузка хрупкий трещины, которые растут до отказа. Трещины всегда начинаются в концентрации напряжений, особенно изменения поперечного сечения изделия, около отверстий и углов при номинальных уровнях напряжения, намного более низких, чем указанные для прочности материала.

Смотрите также

Рекомендации

  1. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 210. ISBN 978-0-07-352938-7.
  2. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 7. ISBN 978-0-07-352938-7.
  3. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 5. ISBN 978-0-07-352938-7.
  4. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. С. 9–10. ISBN 978-0-07-352938-7.
  5. ^ Пиво, Фердинанд Пьер; Джонстон, Элвуд Рассел; Девольф, Джон Т (2009). Механика материалов (5-е изд.). п. 52. ISBN 978-0-07-352938-7.
  6. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 60. ISBN 978-0-07-352938-7.
  7. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. С. 693–696. ISBN 978-0-07-352938-7.
  8. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 47. ISBN 978-0-07-352938-7.
  9. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 49. ISBN 978-0-07-352938-7.
  10. ^ Р. К. Хиббелер (2009). Структурный анализ (7-е изд.). Пирсон Прентис Холл. п. 305. ISBN 978-0-13-602060-8.
  11. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. С. 53–56. ISBN 978-0-07-352938-7.
  12. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. С. 27–28. ISBN 978-0-07-352938-7.
  13. ^ Пиво и Джонстон (2006). Механика материалов (5-е изд.). Макгроу Хилл. п. 28. ISBN 978-0-07-352938-7.

дальнейшее чтение

  • Фа-Хва Ченг, инициалы. (1997). Прочность материала. Огайо: Макгроу-Хилл
  • Механика материалов, Э.Дж. Слышать
  • Альфиревич, Иво. Прочность материалов I. Техничка книга, 1995. ISBN 953-172-010-Х.
  • Альфиревич, Иво. Прочность материалов II. Техничка книга, 1999. ISBN 953-6168-85-5.
  • Эшби, М.Ф. Выбор материалов в дизайне. Пергамон, 1992.
  • Бир, Ф.П., Э.Р. Джонстон и др. Механика материалов, 3-е изд. МакГроу-Хилл, 2001. ISBN 0-07-248673-2
  • Коттрелл, А. Механические свойства вещества. Уайли, Нью-Йорк, 1964 год.
  • Ден Хартог, Джейкоб П. Сопротивление материалов. Dover Publications, Inc., 1961 г., ISBN 0-486-60755-0.
  • Друкер, округ Колумбия Введение в механику деформируемого твердого тела. Макгроу-Хилл, 1967.
  • Гордон, Дж. Новая наука о прочных материалах. Принстон, 1984.
  • Грувер, Микелл П. Основы современного производства, 2-е изд. John Wiley & Sons, Inc., 2002 г. ISBN 0-471-40051-3.
  • Хашеми, Джавад и Уильям Ф. Смит. Основы материаловедения и инженерии, 4-е изд. Макгроу-Хилл, 2006. ISBN 0-07-125690-3.
  • Hibbeler, R.C. Статика и механика материалов, SI Edition. Прентис-Холл, 2004. ISBN 0-13-129011-8.
  • Лебедев, Леонид П. и Майкл Дж. Клауд. Приближение к совершенству: путешествие математика в мир механики. Издательство Принстонского университета, 2004. ISBN 0-691-11726-8.
  • Глава 10 - Прочность эластомеров, А. Гент, W.V. Марс, В: Джеймс Э. Марк, Бурак Эрман и Майк Роланд, редактор (ы), The Science and Technology of Rubber (Fourth Edition), Academic Press, Boston, 2013, Pages 473–516, ISBN 9780123945846, 10.1016 / B978-0-12-394584-6.00010-8
  • Мотт, Роберт Л. Прикладная прочность материалов, 4-е изд. Прентис-Холл, 2002. ISBN 0-13-088578-9.
  • Попов, Егор П. Инженерная механика твердого тела. Prentice Hall, Englewood Cliffs, N.J., 1990. ISBN 0-13-279258-3.
  • Рамамрутам, С. Сопротивление материалов.
  • Шеймс, И. и Ф.А.Козарелли. Анализ упругих и неупругих напряжений. Прентис-Холл, 1991. ISBN 1-56032-686-7.
  • Тимошенко С. Сопротивление материалов, 3-е изд. Krieger Publishing Company, 1976, ISBN 0-88275-420-3.
  • Тимошенко С.П., Янг Д.Х. Элементы сопротивления материалов, 5-е изд. (Система MKS)
  • Дэвидж Р.В., Механическое поведение керамики, Cambridge Solid State Science Series, (1979)
  • Лоун Б.Р. Разрушение хрупких твердых тел, Cambridge Solid State Science Series, 2-е изд. (1993)
  • Грин Д. Введение в механические свойства керамики, Cambridge Solid State Science Series, Eds. Кларк, Д. Р., Суреш, С., Уорд, И. М. Бабу Том К. (1998)

внешняя ссылка