WikiDer > Деформация (инженерия)

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Деформационная» инженерия – Новости · газеты · книги · ученый · JSTOR (Сентябрь 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Напряжение сжатия приводит к деформации, которая укорачивает объект, но также расширяет его наружу.

В инженерное дело, деформация относится к изменению размера или формы объекта. Смещения являются абсолютный изменение положения точки на объекте. Прогиб относительное изменение внешних перемещений объекта. Напряжение это относительный внутреннее изменение формы бесконечно маленького куба материала и может быть выражено как безразмерное изменение длины или угла искажения куба. Деформации связаны с силами, действующими на куб, которые известны как стресс, автор кривая напряжения-деформации. Взаимосвязь между напряжением и деформацией обычно линейна и обратима до тех пор, пока предел текучести и деформация эластичный. Линейная зависимость для материала известна как Модуль для младших. Выше предела текучести после разгрузки остается некоторая необратимая деформация, которая называется Пластическая деформация. Определение напряжения и деформации во всем твердом объекте дается полем сопротивление материалов а для структуры структурный анализ.

Инженерный стресс и инженерное напряжение являются приближениями к внутреннему состоянию, которое может быть определено по внешним силам и деформациям объекта, при условии, что нет значительного изменения размера. При значительном изменении размера настоящий стресс и истинное напряжение может быть получен из мгновенного размера объекта.

На рисунке видно, что сжимающая нагрузка (указанная стрелкой) вызвала деформацию в цилиндр так что исходная форма (пунктирные линии) изменилась (деформировалась) в форму с выпуклыми сторонами. Боковые стороны выступают из-за того, что материал, хотя и достаточно прочный, чтобы не трескаться или иным образом не разрушаться, недостаточно прочен, чтобы выдержать нагрузку без изменений. В результате материал вытесняется вбок. Внутренние силы (в данном случае под прямым углом к ​​деформации) противостоят приложенной нагрузке.

Концепция жесткое тело может применяться, если деформация незначительна.

Виды деформации

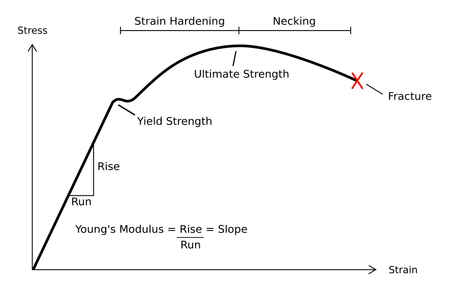
В зависимости от типа материала, размера и геометрии объекта, а также приложенных сил могут возникнуть различные типы деформации. На изображении справа показана диаграмма зависимости инженерного напряжения от деформации для типичного пластичного материала, такого как сталь. Различные режимы деформации могут возникать в разных условиях, что можно изобразить с помощью карта механизма деформации.

Постоянная деформация необратима; деформация сохраняется даже после снятия приложенных сил, в то время как временная деформация восстанавливается, поскольку она исчезает после снятия приложенных сил. Временная деформация также называется эластичный деформация, а остаточная деформация называется пластик деформация.

Типичная диаграмма зависимости напряжения от деформации, показывающая различные стадии деформации.

Упругая деформация

Исследование временной или упругой деформации в случае инженерное напряжение применяется к материалам, используемым в машиностроении и строительстве, таких как конкретный и стали, которые подвергаются очень небольшим деформациям. Инженерное напряжение моделируется теория бесконечно малых деформаций, также называемый теория малых деформаций, теория малых деформаций, теория малых перемещений, или же теория малого смещения-градиента где деформации и вращения малы.

Для некоторых материалов, например эластомеры и полимеры, подверженные большим деформациям, инженерное определение деформации неприменимо, например типичные инженерные деформации более 1%,^[1] поэтому требуются другие более сложные определения деформации, такие как протяжение, логарифмическая деформация, Зеленый штамм, и Штамм альманси. Эластомеры и память формы металлы, такие как Нитинол проявляют большие диапазоны упругой деформации, как и резинка. Однако в этих материалах упругость нелинейна.

Обычные металлы, керамика и большинство кристаллов демонстрируют линейную упругость и меньший диапазон упругости.

Линейная упругая деформация регулируется Закон Гука, в котором говорится:

${ displaystyle sigma = E varepsilon}$

Где ${ displaystyle sigma}$ применяется стресс, ${ displaystyle E}$ материальная постоянная, называемая Модуль для младших или же модуль упругости, а ε - результат напряжение. Это соотношение применяется только в диапазоне упругости и указывает на то, что наклон кривой зависимости напряжения от деформации можно использовать для определения модуля Юнга (${ displaystyle E}$). Инженеры часто используют этот расчет при испытаниях на растяжение.

Обратите внимание, что не все эластичные материалы подвергаются линейной упругой деформации; некоторые, такие как конкретный, серый чугун, и многие полимеры реагируют нелинейным образом. Для этих материалов закон Гука неприменим.^[2]

Истинный стресс и напряжение

Поскольку мы не принимаем во внимание изменение площади во время деформации, описанной выше, истинную кривую напряжений и деформаций следует восстановить. Для построения кривой напряжения-деформации мы можем предположить, что изменение объема равно 0, даже если мы деформировали материалы. Можно предположить, что:

${ displaystyle A_ {i} times varepsilon _ {i} = A_ {f} times varepsilon _ {f}}$

Тогда истинное напряжение можно выразить следующим образом:

${ displaystyle sigma _ {T} = F / A_ {f} = F / A_ {i} times A_ {i} / A_ {f} = sigma _ {e} times l_ {f} / l_ { i} = sigma _ {E} times { frac {l_ {i} + delta l} {l_ {i}}} = sigma _ {E} (1+ varepsilon _ {E})}$

Кроме того, истинная деформация ε_Т можно выразить следующим образом:

${ displaystyle varepsilon _ {T} = { frac {dl} {l_ {0}}} + { frac {dl} {l_ {1}}} + { frac {dl} {l_ {2}} } + cdots = sum _ {i} { frac {dl} {l_ {i}}}}$

Тогда мы можем выразить значение как

${ displaystyle int _ {l_ {0}} ^ {l_ {i}} { frac {dl} {l}} , dx = ln left ({ frac {l_ {i}} {l_ { 0}}} right) = ln (1+ varepsilon _ {E})}$

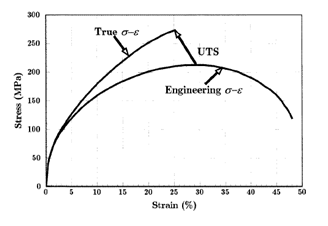
Таким образом, мы можем вызвать сюжет с точки зрения ${ displaystyle sigma _ {T}}$ и ${ displaystyle varepsilon _ {E}}$ как на правильном рисунке.

Кроме того, на основе истинной кривой напряжения-деформации мы можем оценить область, в которой начинается образование шейки. Поскольку образование шейки начинается после предельного напряжения растяжения, когда прилагается максимальная сила, мы можем выразить эту ситуацию следующим образом:

${ displaystyle dF = 0 = sigma _ {T} dA_ {i} + A_ {i} d sigma _ {T}}$

так что эту форму можно выразить следующим образом:

${ displaystyle { frac {d sigma _ {T}} { sigma _ {T}}} = - { frac {dA_ {i}} {A_ {i}}}}$

Это указывает на то, что шейка начинает появляться там, где уменьшение площади становится более значительным по сравнению с изменением напряжения. Тогда напряжение будет локализовано в определенной области, где появляется шейка.

Кроме того, мы можем вызвать различные зависимости на основе истинной кривой напряжения-деформации.

1) Истинная кривая деформации и напряжения может быть выражена приблизительной линейной зависимостью путем регистрации истинных напряжений и деформаций. Отношение можно выразить следующим образом:

${ Displaystyle sigma _ {T} = K times ( varepsilon _ {T}) ^ {n}}$

Где ${ displaystyle K}$ коэффициент напряжения и ${ displaystyle n}$ - коэффициент деформационного упрочнения. Обычно значение ${ displaystyle n}$ имеет диапазон от 0,02 до 0,5 при комнатной температуре. Если ${ displaystyle n}$ равно 1, мы можем выразить этот материал как идеальный эластичный материал.^[3][4]

2) На самом деле, напряжение также сильно зависит от скорости изменения деформации. Таким образом, мы можем вывести эмпирическое уравнение на основе изменения скорости деформации.

${ displaystyle sigma _ {T} = K ' times ({ dot { varepsilon _ {T}}}) ^ {m}}$

Кривая истинного напряжения-деформации металла FCC и его производной формы^[3]

Где ${ displaystyle K '}$ постоянна, связанная с напряжением течения материала. ${ displaystyle { dot { varepsilon _ {T}}}}$ указывает производную деформации по времени, которая также известна как скорость деформации. ${ displaystyle m}$ - чувствительность к скорости деформации. Кроме того, стоимость ${ displaystyle m}$ связано с сопротивлением шейке. Обычно значение ${ displaystyle m}$ находится в диапазоне 0-0,1 при комнатной температуре и достигает 0,8 при повышении температуры.

Объединив пункты 1) и 2), мы можем создать окончательную связь, как показано ниже:

${ displaystyle sigma _ {T} = K '' times ( varepsilon _ {T}) ^ {n} ({ dot { varepsilon _ {T}}}) ^ {m}}$

Где ${ displaystyle K ''}$ - глобальная константа для связи деформации, скорости деформации и напряжения.

3) Основываясь на истинной кривой напряжения-деформации и ее производной форме, мы можем оценить деформацию, необходимую для начала образования шейки. Это можно рассчитать на основе пересечения истинной кривой напряжения-деформации, как показано справа.

На этом рисунке также показана зависимость деформации сужения при различных температурах. В случае металлов с ГЦК обе кривые зависимости деформации от напряжения при ее производной сильно зависят от температуры. Поэтому при более высокой температуре образование шейки начинает появляться даже при более низком значении деформации.

Все эти свойства указывают на важность расчета истинной кривой напряжения-деформации для дальнейшего анализа поведения материалов в неожиданных условиях окружающей среды.

4) Графический метод, так называемое «конструктивное рассмотрение», может помочь определить поведение кривой напряжения-деформации независимо от того, происходит ли образование шейки или вытягивание на образце. Установив ${ displaystyle lambda = L / L_ {0}}$в качестве определяющего фактора истинное напряжение и деформация могут быть выражены с помощью инженерных напряжений и деформаций, как показано ниже:

${ displaystyle sigma _ {T} = sigma _ {e} times lambda, qquad varepsilon _ {T} = ln lambda.}$

Следовательно, значение инженерного напряжения может быть выражено секущей линией от истинного напряжения и ${ displaystyle lambda}$ значение где ${ displaystyle lambda = 0}$ к ${ displaystyle lambda = 1}$. Анализируя форму ${ displaystyle sigma _ {T} - lambda}$ диаграмму и секущую линию, мы можем определить, показывают ли материалы рисунок или шейку.

Рассмотрим участок. (а) Истинная кривая напряжения-деформации без касательных. Нет ни шейки, ни рисунка. (б) С одной касательной. Есть только шейка. (c) С двумя касательными. Есть и шейка, и рисунок.^[5]

На рисунке (а) виден только вогнутый вверх участок Консидера. Это указывает на то, что нет падения текучести, поэтому материал будет разрушен до того, как он подойдет. На рисунке (b) есть конкретная точка, где касательная совпадает с секущей линией в точке, где ${ displaystyle lambda = lambda _ {Y}}$. После этого значения наклон становится меньше, чем секущая линия, на которой начинает появляться шейка. На рисунке (c) есть точка, где начинает проявляться податливость, но когда ${ displaystyle lambda = lambda _ {d}}$, рисунок происходит. После рисования весь материал растянется и в конечном итоге покажет трещину. Между ${ displaystyle lambda _ {Y}}$ и ${ displaystyle lambda _ {d}}$, сам материал не растягивается, а начинает вытягиваться только шея.

Пластическая деформация

Лист из высокопрочной низколегированной стали марки Swebor, показывающий обе стороны, после пластической деформации от поражения снаряды в баллистика тестирование. Примечание: при воздействии огня сталь сначала расширяется, а затем теряет свою прочность, превышая критическую температуру при 538 ° C или 1000 ° F на ASTM E119 если не лечить с огнезащита.

Этот тип деформации нельзя устранить простым удалением приложенной силы. Однако объект в диапазоне пластической деформации сначала подвергнется упругой деформации, которую можно устранить, просто сняв приложенную силу, так что объект частично вернется к своей исходной форме. Мягкий термопласты имеют довольно большой диапазон пластической деформации, как и пластичные металлы, такие как медь, серебро, и золото. Стали тоже, но не чугун. Твердые термореактивные пластмассы, резина, кристаллы и керамика имеют минимальные интервалы пластической деформации. Примером материала с большим диапазоном пластической деформации является влажный жевательная резинка, который можно растянуть в десятки раз по сравнению с исходной длиной.

Под действием растягивающего напряжения пластическая деформация характеризуется деформационное упрочнение регион и шею область и, наконец, перелом (также называемый разрывом). При деформационном упрочнении материал укрепляется за счет движения атомные дислокации. Фаза образования шейки обозначается уменьшением площади поперечного сечения образца. Сужение шеи начинается после достижения максимальной прочности. Во время образования шейки материал больше не может выдерживать максимальное напряжение, и напряжение в образце быстро увеличивается. Пластическая деформация заканчивается разрушением материала.

Усталость металла

Другой механизм деформации: усталость металла, который встречается в основном в пластичный металлы. Первоначально считалось, что материал, деформируемый только в пределах диапазона упругости, полностью возвращается в исходное состояние после устранения сил. Однако с каждой деформацией на молекулярном уровне появляются ошибки. После многих деформаций начнут появляться трещины, за которыми вскоре последует перелом, без видимой пластической деформации между ними. В зависимости от материала, формы и того, насколько близко к пределу упругости он деформируется, разрушение может потребовать тысяч, миллионов, миллиардов или триллионов деформаций.

Усталость металла была основной причиной отказов самолетов, особенно до того, как этот процесс был хорошо понят (см., Например, Аварии De Havilland Comet). Есть два способа определить, когда детали угрожает усталость металла: либо предсказать, когда произойдет отказ из-за комбинации материала / силы / формы / итераций, и заменить уязвимые материалы до того, как это произойдет, либо выполнить проверки для обнаружения микроскопических трещин и произведите замену, как только они возникнут. Выбор материалов, которые не подвержены усталости металла в течение срока службы продукта, является лучшим решением, но не всегда возможным. Избегание форм с острыми углами ограничивает усталость металла за счет снижения концентрации напряжений, но не устраняет ее.

Анализ фактор выпуклости частей самолета, находящихся под давлением, может помочь в оценке устойчивости к повреждению планер фюзеляжи.^[6]

Схема кривая напряжение – деформация, показывающий взаимосвязь между напряжением (приложенной силой) и деформацией (деформацией) пластичного металла.

Разрушение при сжатии

Обычно сжимающее напряжение, прикладываемое к стержням, столбцыи т.д. приводит к укорачиванию.

Нагрузка на структурный элемент или образец увеличивает сжимающее напряжение до тех пор, пока не достигнет своего предела. прочность на сжатие. По свойствам материала режимы разрушения бывают уступающий для материалов с пластичный поведение (большинство металлы, немного почвы и пластмассы) или разрыв из-за хрупкого поведения (геоматериалы, чугун, стекло, так далее.).

В длинных тонких конструктивных элементах, таких как колонны или ферма бары - увеличение сжимающей силы F приводит к структурный отказ из-за коробление при меньшем напряжении, чем прочность на сжатие.

Перелом

Этот вид деформации также необратим. Разрыв происходит после того, как материал достигает конца диапазона упругой, а затем пластической деформации. В этот момент силы накапливаются, пока их не станет достаточно, чтобы вызвать перелом. При приложении достаточных усилий все материалы в конечном итоге разрушатся.

Заблуждения

Распространенное заблуждение состоит в том, что все материалы, которые гнутся, «слабые», а те, которые не гнутся, - «прочные». В действительности многие материалы, которые подвергаются большим упругим и пластическим деформациям, например сталь, способны поглощать напряжения, которые могут вызвать разрушение хрупких материалов, таких как стекло, с минимальным диапазоном пластической деформации.^[7]

Смотрите также

Рекомендации