WikiDer > Математика судоку
Пазлы судоку можно изучить математически чтобы ответить на такие вопросы, как "Сколько существует заполненных решеток судоку?", "Какое минимальное количество подсказок в правильной головоломке?" и «Каким образом сетки судоку могут быть симметричными?» за счет использования комбинаторика и теория групп.
Основные результаты заключаются в том, что для классического судоку количество заполненных сеток равно 6,670,903,752,021,072,936,960 (6.67×1021), что сводится к 5,472,730,538 существенно разные группы под преобразования, сохраняющие достоверность. Существует 26 типов симметрии, но их можно найти только примерно в 0,005% всех заполненных сеток. Головоломка с уникальным решением должна иметь не менее 17 подсказок, и есть решаемая головоломка с не более чем 21 ключом для каждой решенной сетки. Самая большая минимальная головоломка, найденная на данный момент, содержит 40 ключей.
Подобные результаты известны для вариантов и меньших сеток. Нет точных результатов для судоку, большего, чем классическая сетка 9 × 9, хотя есть оценки, которые считаются довольно точными.
Обзор
Анализ судоку делится на две основные области: анализ свойств (1) готовых сеток и (2) головоломок. Первоначальный анализ был в основном сосредоточен на перечислении решений, и результаты впервые появились в 2004 году.[1]
Есть много Варианты судоку, частично характеризуется размером (N), а форма их регионы. Если не указано иное, обсуждение в этой статье предполагает классическую судоку, т.е. N= 9 (сетка 9 × 9 и области 3 × 3). В прямоугольном судоку используются прямоугольные области размерности строка-столбец. р×C. Другие варианты включают варианты с участками неправильной формы или с дополнительными ограничениями (гиперкуб) или различные типы ограничений (Самунамупуре).
Регионы также называют блоки или же коробки. А группа является частью сетки, содержащей 3 строки и 3 блока, а куча является частью сетки, которая включает 3 столбца и 3 поля. А головоломка является частично завершенным сетка, а начальные значения равны данность или же подсказки. А правильный Пазл имеет уникальное решение. А минимальный Puzzle - это настоящая головоломка, от которой невозможно избавиться без дополнительных решений. Видеть Глоссарий судоку для другой терминологии.[2]
Решение судоку с точки зрения игрока было исследовано в книге Дени Бертье «Скрытая логика судоку» (2007).[3] который рассматривает такие стратегии, как «скрытые xy-цепи».
Математический контекст
Общая проблема решения головоломок судоку на п2×п2 сетки п×п блоки, как известно, НП-полный.[4] За п= 3 (классическая судоку), однако этот результат не имеет большого практического значения: алгоритмы Такие как Танцы Links может решать головоломки за доли секунды из-за небольшого размера задачи.[нужна цитата]
Загадку можно выразить как раскраска графика проблема.[5] Цель состоит в том, чтобы построить 9-раскраску конкретного графа с помощью частичной 9-раскраски. В Судоку граф имеет 81 вершину, по одной вершине на каждую ячейку. Вершины помечены упорядоченными парами (Икс, у), куда Икс и у - целые числа от 1 до 9. В этом случае две различные вершины, помеченные (Икс, у) и (Икс′, у′) Соединены ребром тогда и только тогда, когда:
- Икс = Икс′ (Тот же столбец) или,
- у = у′ (Тот же ряд) или,
- ⌈ Икс/3 ⌉ = ⌈ Икс′ / 3 ⌉ и ⌈ у/3 ⌉ = ⌈ у′ / 3 ⌉ (та же ячейка 3 × 3)
Затем головоломка завершается присвоением каждой вершине целого числа от 1 до 9 таким образом, чтобы вершинам, соединенным ребром, не было присвоено одно и то же целое число.
Сетка решения судоку также является Латинский квадрат.[5] Решеток судоку значительно меньше, чем латинских квадратов, потому что судоку накладывает дополнительные региональные ограничения.
Судоку из групповых столов
Как и в случае с Латинские квадраты (дополнение- или) таблицы умножения (Столы Кэли) конечных групп можно использовать для построения судоку и связанных таблиц чисел. А именно надо брать подгруппы и факторгруппы в учетную запись:
Взять к примеру группу пар, добавляя каждый компонент отдельно по модулю некоторого . Пропустив один из компонентов, мы внезапно попадаем в (и это отображение, очевидно, совместимо с соответствующими дополнениями, т.е. групповой гомоморфизмТакже говорится, что последний факторгруппа первого, потому что некоторые когда-то разные элементы становятся равными в новой группе. подгруппа, потому что мы можем просто заполнить недостающий компонент вернуться к .
В соответствии с этим представлением мы запишем пример, Сетка 1, за .
Каждая область судоку выглядит одинаково во втором компоненте (а именно, как подгруппа ), потому что они добавляются независимо от первого. С другой стороны, первые компоненты равны в каждом блоке, и если мы представим каждый блок как одну ячейку, эти первые компоненты показывают один и тот же образец (а именно факторгруппу ). Как указано в статье Латинские квадраты, это латинский квадрат порядка .
Теперь, чтобы получить судоку, давайте переставим строки (или, что эквивалентно, столбцы) таким образом, чтобы каждый блок перераспределялся ровно один раз в каждый блок - например, упорядочим их Это, конечно, сохраняет свойство латинского квадрата. Кроме того, в каждом блоке линии имеют отдельный первый компонент по построению, и каждая строка в блоке имеет отдельные записи через второй компонент, потому что вторые компоненты блоков изначально образовывали латинский квадрат порядка. (из подгруппы ). Таким образом, мы приходим к судоку (переименуйте пары в числа 1 ... 9, если хотите). Используя приведенный выше пример и перестановку строк, мы приходим к Сетка 2.
|
|
Чтобы этот метод работал, обычно не требуется продукт двух групп одинакового размера. Так называемый короткий точная последовательность конечных групп подходящего размера уже выполняет свою работу. Попробуйте например группу с фактор- и подгруппой Кажется очевидным (уже из аргументов перечисления), что не все судоку можно сгенерировать таким образом.
Варианты
Судоку можно интерпретировать как черепица (или же крышка) из Латинский квадрат с полимино (в регионы судоку). Классическая судоку 9 × 9 состоит из квадратных нономино. Правила судоку можно применять к головоломкам других размеров, но только N2×N2 Пазлы судоку можно выложить квадратными полимино.
Увидеть Глоссарий судоку для расширенного списка вариантов.
Прямоугольные области
Популярный вариант - прямоугольные области (блоки или же коробки) - например, 2 × 3 гексомино выложенный плиткой в сетке 6 × 6. При обсуждении этого варианта используются следующие обозначения:
- р×C обозначает прямоугольную область с р ряды и C столбцы.
- Подразумеваемая конфигурация сетки включает:
- размеры сетки N×N, куда N = р×C
- N блоки (коробки) размера р×C, расположенные в C×р 'суперсеть'
- C группы размера р×N, состоящий из р горизонтально смежные блоки
- р стеки размера N×C, состоящий из C вертикально смежные блоки
Судоку с квадратом N×N области более симметричны, чем прямоугольные судоку, поскольку каждая строка и столбец пересекаются N регионы и акции N ячеек с каждым. Количество лент и стопок также равно N. Судоку «3 × 3» дополнительно уникален: N также количество ограничений области строки-столбца из Одно правило (т.е. есть N= 3 типа единицы).
Пазл-судокус
Судоку, области которого (не обязательно) квадратные или прямоугольные, известны как Судоку-головоломка. В частности, N×N квадрат, где N Prime можно облицовывать плиткой только неправильной формы N-омино. Для малых значений N количество способов выложить квадрат (исключая симметрии) было вычислено (последовательность A172477 в OEIS).[6] За N ≥ 4 некоторые из этих мозаик несовместимы ни с одним латинским квадратом; т.е. все головоломки судоку на такой плитке не имеют решения.[6]
Решения
Ответ на вопрос «Сколько существует сеток судоку?» зависит от определения того, когда похожие решения считаются разными.
Обычные судоку
Все решения
Для перечисления все возможных решений, два решения считаются различными, если любое из их соответствующих (81) значений ячейки различается. Соотношения симметрии между подобными решениями игнорируются, например повороты решения считаются различными. Симметрии играют важную роль в стратегии перечисления, но не при подсчете все возможные решения.
Первое известное решение для полного перебора было опубликовано QSCGZ (Guenter Stertenbrink) в rec.puzzles группа новостей в 2003 г.,[7][8][9] получение 6,670,903,752,021,072,936,960 (6.67×1021) различных решений.
В исследовании 2005 года Фельгенгауэр и Джарвис[10][9] проанализировал перестановки верхней полосы, используемой в действительных решениях. Однажды Band1 симметрии и классы эквивалентности для частичных сеточных решений были определены, завершения двух нижних полос были построены и подсчитаны для каждого класса эквивалентности. Суммирование завершений по классам эквивалентности, взвешенное по размеру класса, дает общее количество решений как 6 670 903 752 021 072 936 960, что подтверждает значение, полученное QSCGZ. Впоследствии это значение было подтверждено несколько раз независимо. Позже был разработан второй метод подсчета, основанный на генерации полос, который требует значительно меньших вычислительных ресурсов. Этот последующий метод привел к тому, что потребовалось примерно 1/97 от числа циклов вычислений по сравнению с исходными методами, но его было значительно сложнее настроить.
Принципиально разные решения
Преобразования, сохраняющие валидность
Две действующие сетки по сути то же самое, если одно может быть получено из другого, используя так называемый преобразование с сохранением достоверности (VPT). Эти преобразования всегда преобразуют действительную сетку в другую действительную сетку. Существует два основных типа: перестановка символов (перемаркировка) и перестановка ячеек (перестановка). Они есть:
- Переназначение символов (9!)
(После исключения всех возможных комбинаций перемаркировки, кроме одной: например, при фиксированном значении верхнего ряда [123456789], количество фиксированных сеток уменьшается до 18 383 222 420 692 992. Это значение равно 6 670 903 752 021 072 936 960, разделенному на 9!
и перестановка (перетасовка):
- Перестановки полос (3!)
- Перестановки строк внутри полосы (3! × 3! × 3!)
- Перестановки стека (3!)
- Перестановки столбцов в стеке (3! × 3! × 3!)
- Отражение, транспонирование и вращение (2)
(При однократном транспонировании или повороте на четверть оборота в сочетании с вышеуказанными перестановками может быть произведена любая комбинация отражений, транспозиций и поворотов, поэтому эти операции вносят вклад только в 2 раза)
Эти операции определяют отношение между эквивалентными сетками. Что касается 81 значения ячейки сетки, операции перестановки образуют подгруппа из симметричная группа S81, порядка 3!8× 2 = 3 359 232. Операции по перемаркировке изоморфный с S9 и сгенерируйте еще 9! = 362880 эквивалентных сеток. Применение этих операций к сетке дает 3!8× 2 × 9! или 1,218,998,108,160 по существу эквивалентных сетей. Однако существует небольшое количество судоку, для которых вышеуказанные операции генерируют меньше сеток; это самоподобные, или автоморфный судоку. Только около 0,01% всех уникальных сеток являются автоморфными.[11], но их подсчет необходим для определения точного количества существенно разных судоку.
Группа симметрии судоку
Точная структура симметрии судоку группа можно кратко выразить с помощью венок (≀). Возможные перестановки строк (или столбцов) образуют группу изоморфный к S3 ≀ S3 порядка 3!4 = 1,296[12]. Вся группа перегруппировки формируется путем разрешения операции транспонирования (изоморфной C2) воздействуют на две копии этой группы, одну для перестановок строк и одну для перестановок столбцов. Это S3 ≀ S3 ≀ C2, группа порядка 12962 × 2 = 3 359 232. Наконец, операции перемаркировки переключаются с операциями перестановки, поэтому полная группа soduku (VPT) равна (S3 ≀ S3 ≀ C2) × S9 заказа 1,218,998,108,160.
Неподвижные точки и лемма Бернсайда
Набор эквивалентных сеток, которые могут быть достигнуты с помощью этих операций (за исключением перемаркировки), образует орбита сеток под действием перестановки группа. Количество существенно различных решений - это количество орбит, которое можно вычислить с помощью Лемма Бернсайда. Бернсайд фиксированные точки сетки, которые либо не изменяются при операции перестановки, либо отличаются только перемаркировкой. Для упрощения расчета элементы группы перестановок разделены на классы сопряженности, элементы которого имеют одинаковое количество неподвижных точек. Оказывается, только 27 из 275 классов сопряженности группы перестановок имеют неподвижные точки.[13]; Эти классы сопряженности представляют различные типы симметрии (самоподобие или автоморфизм), которые можно найти в завершенных сетках судоку. Используя эту технику, Эд Рассел и Фрейзер Джарвис были первыми, кто вычислил количество существенно различных решений судоку как 5,472,730,538[13][14].
| Имя или состав[15] | Код | Учебный класс Идентификатор.[13] | Учебный класс размер[13] | Клеточные циклы | О | F | Количество фиксированных сетей (до перемаркировки), за элемент[13] | Количество фиксированных сетей, за элемент | Количество фиксированных сетей (до перемаркировки), весь класс | Количество фиксированных сетей, весь класс |
|---|---|---|---|---|---|---|---|---|---|---|
| Личность | е | 1 | 1 | 1 | 81 | 18,383,222,420,692,992 | 6,670,903,752,021,072,936,960 | 18,383,222,420,692,992 | 6,670,903,752,021,072,936,960 | |
| Мини-тяги (MR) | ccc | 8 | 16 | 27×3 | 3 | 0 | 107,495,424 | 39,007,939,461,120 | 1,719,926,784 | 624,127,031,377,920 |
| 2 MR, 1 MD | ccc | c | 7 | 96 | 27×3 | 3 | 0 | 21,233,664 | 7,705,271,992,320 | 2,038,431,744 | 739,706,111,262,720 |
| 1 MR, 2 MD | ccc | cc | 9 | 192 | 27×3 | 3 | 0 | 4,204,224 | 1,525,628,805,120 | 807,211,008 | 292,920,730,583,040 |
| Мини-диагонали (MD) | ccc | ccc | 10 | 64 | 27×3 | 3 | 0 | 2,508,084 | 910,133,521,920 | 160,517,376 | 58,248,545,402,880 |
| Тяги в прыжке (JR) | C | 25 | 144 | 27×3 | 3 | 0 | 14,837,760 | 5,384,326,348,800 | 2,136,637,440 | 775,342,994,227,200 |
| 2 JR, 1 GR | C | c | 28 | 864 | 27×3 | 3 | 0 | 2,085,120 | 756,648,345,600 | 1,801,543,680 | 653,744,170,598,400 |
| 1 младший, 2 гр | C | cc | 30 | 1,728 | 27×3 | 3 | 0 | 294,912 | 107,017,666,560 | 509,607,936 | 184,926,527,815,680 |
| Гребля на скольжение (GR) | C | ccc | 32 | 1,152 | 27×3 | 3 | 0 | 6,342,480 | 2,301,559,142,400 | 7,306,536,960 | 2,651,396,132,044,800 |
| Полные ряды (FR) | C9 | 27 | 288 | 9×9 | 9 | 0 | 5,184 | 1,881,169,920 | 1,492,992 | 541,776,936,960 |
| 2 FR, 1 WR | C9 | c | 26 | 1,728 | 9×9 | 9 | 0 | 2,592 | 940,584,960 | 4,478,976 | 1,625,330,810,880 |
| 1 FR, 2 WR | C9 | cc | 29 | 3,456 | 9×9 | 9 | 0 | 1,296 | 470,292,480 | 4,478,976 | 1,625,330,810,880 |
| Размахивая рядами (WR) | C9 | ccc | 31 | 2,304 | 9×9 | 9 | 0 | 648 | 235,146,240 | 1,492,992 | 541,776,936,960 |
| Прыжки по диагонали (JD) | C | C | 22 | 5,184 | 27×3 | 3 | 0 | 323,928 | 117,546,992,640 | 1,679,242,752 | 609,363,609,845,760 |
| Сломанные колонны (BC) | C | C9 | 24 | 20,736 | 9×9 | 9 | 0 | 288 | 104,509,440 | 5,971,968 | 2,167,107,747,840 |
| Полные диагонали (FD) | C9 | C9 | 23 | 20,736 | 9×9 | 9 | 0 | 162 | 58,786,560 | 3,359,232 | 1,218,998,108,160 |
| Диагональное зеркало (DM) | Т | 37 | 1,296 | 36×2 | 2 | 9 | 30,258,432 | 10,980,179,804,160 | 39,214,927,872 | 14,230,313,026,191,360 |
| DM + MD | T ccc | 40 | 10,368 | 3×3, 12×6 | 6 | 0 | 1,854 | 672,779,520 | 19,222,272 | 6,975,378,063,360 |
| DM + JD | Т С | 43 | 93,312 | 3×3, 12×6 | 6 | 0 | 288 | 104,509,440 | 26,873,856 | 9,751,984,865,280 |
| Четверть оборота (QT) | T sS | 86 | 69,984 | 20×4 | 4 | 1 | 13,056 | 4,737,761,280 | 913,711,104 | 331,567,485,419,520 |
| Половина оборота (HT) | sS | SS | 79 | 2,916 | 40×2 | 2 | 1 | 155,492,352 | 56,425,064,693,760 | 453,415,698,432 | 164,535,488,647,004,160 |
| Стойки для колонн (CS) | S | sss | 134 | 972 | 36×2 | 2 | 9 | 449,445,888 | 163,094,923,837,440 | 436,861,403,136 | 158,528,265,969,991,680 |
| CS + MC | cS6 | sss | 135 | 3,888 | 3×3, 12×6 | 6 | 0 | 27,648 | 10,032,906,240 | 107,495,424 | 39,007,939,461,120 |
| CS + GR | cS6 | C6 | 142 | 31,104 | 3×3, 12×6 | 6 | 0 | 6,480 | 2,351,462,400 | 201,553,920 | 73,139,886,489,600 |
| CS + JR / B2, GR / B13 | S6 | C6 | 143 | 15,552 | 3×3, 12×6 | 6 | 0 | 1,728 | 627,056,640 | 26,873,856 | 9,751,984,865,280 |
| CS + GR / Band2, JR / B13 | cS | C6 | 144 | 15,552 | 3×3, 12×6 | 6 | 0 | 3,456 | 1,254,113,280 | 53,747,712 | 19,503,969,730,560 |
| CS + JR | S | C6 | 145 | 7,776 | 3×3, 12×6 | 6 | 0 | 13,824 | 5,016,453,120 | 107,495,424 | 39,007,939,461,120 |
| (нетривиально) | 949,129,933,824 | 344,420,270,386,053,120 | ||||||||
| общий | 18,384,171,550,626,816 | 6,671,248,172,291,458,990,080 |
Обратите внимание, что сетка может быть фиксированной точкой нескольких преобразований одновременно; например, любая сетка с четвертьоборотной симметрией также имеет полуоборотную симметрию. Комбинация всех преобразований, фиксирующих конкретную сетку, является подгруппа стабилизатора («группа автоморфизмов») этой сетки.
Подгруппы стабилизаторов
Рассел составил список из 122 «существенно разных» нетривиальных подгруппа стабилизатора классы сопряженности («группы автоморфизмов»),[16][17] наряду с примерной сеткой, классы сопряженности VPT в группе, набор генераторов и количество существенно различных сеток (орбит) с этим классом стабилизатора. С точностью до изоморфизма существует 26 различных групповых структур.[18] Существует 15 различных возможных размеров группы стабилизаторов, перечисленных в следующем разделе.
Количество принципиально эквивалентных сеток
Каждую из уникальных сеток можно анализировать.[11] самоподобия («автоморфизмы») для оценки «недостатка» в количестве существенно эквивалентных сеток. Результаты представлены в таблице ниже. Всего 560 151 из 5 472 730 538 существенно уникальных сеток (около 0,01%) имеют форму самоподобия (нетривиальный стабилизатор).
Размер орбиты (то есть количество практически эквивалентных сеток) можно рассчитать с помощью теорема о стабилизаторе орбиты: это размер группы симметрии судоку, деленный на размер группы стабилизатора (или «автоморфизма»). Умножение количества по существу уникальных сеток (количества орбит) на размер орбиты дает общее количество сеток с этим размером группы стабилизаторов; суммирование снова дает общее количество возможных сеток судоку. «Автоморфные» сетки имеют меньшие орбиты, поэтому вероятность того, что случайная сетка имеет симметрию, падает: примерно от 1 из 10 000 для существенно разных сеток до примерно 1 из 20 000 для всех сеток.
| Размер стабилизатор группа | Количество по существу уникальные сетки (количество витков) | Эквивалентные сетки (размер орбиты), игнорирование перемаркировки | Количество сеток, игнорирование перемаркировки | Эквивалентные сетки (размер орбиты), включая перемаркировку | Общее количество сеток |
|---|---|---|---|---|---|
| 1 | 5,472,170,387 | 3,359,232 | 18,382,289,873,462,784 | 1,218,998,108,160 | 6,670,565,349,282,175,057,920 |
| 2 | 548,449 | 1,679,616 | 921,183,715,584 | 609,499,054,080 | 334,279,146,711,121,920 |
| 3 | 7,336 | 1,119,744 | 8,214,441,984 | 406,332,702,720 | 2,980,856,707,153,920 |
| 4 | 2,826 | 839,808 | 2,373,297,408 | 304,749,527,040 | 861,222,163,415,040 |
| 6 | 1,257 | 559,872 | 703,759,104 | 203,166,351,360 | 255,380,103,659,520 |
| 8 | 29 | 419,904 | 12,177,216 | 152,374,763,520 | 4,418,868,142,080 |
| 9 | 42 | 373,248 | 15,676,416 | 135,444,234,240 | 5,688,657,838,080 |
| 12 | 92 | 279,936 | 25,754,112 | 101,583,175,680 | 9,345,652,162,560 |
| 18 | 85 | 186,624 | 15,863,040 | 67,722,117,120 | 5,756,379,955,200 |
| 27 | 2 | 124,416 | 248,832 | 45,148,078,080 | 90,296,156,160 |
| 36 | 15 | 93,312 | 1,399,680 | 33,861,058,560 | 507,915,878,400 |
| 54 | 11 | 62,208 | 684,288 | 22,574,039,040 | 248,314,429,440 |
| 72 | 2 | 46,656 | 93,312 | 16,930,529,280 | 33,861,058,560 |
| 108 | 3 | 31,104 | 93,312 | 11,287,019,520 | 33,861,058,560 |
| 162 | 1 | 20,736 | 20,736 | 7,524,679,680 | 7,524,679,680 |
| 648 | 1 | 5,184 | 5,184 | 1,881,169,920 | 1,881,169,920 |
| >1 | 560,151 | 932,547,230,208 | 338,402,738,897,879,040 | ||
| 5,472,730,538 | 18,383,222,420,692,992 | 6,670,903,752,021,072,936,960 |
Другие варианты
Были рассчитаны результаты подсчета для многих вариантов судоку: они кратко изложены ниже.
Судоку с дополнительными ограничениями
Ниже приведены все ограничения классической судоку 3 × 3 (сетка 9 × 9). Имена типов не стандартизированы: щелкните ссылки атрибуции, чтобы просмотреть определения. Обычный Содуку включен в последнюю строку для сравнения.
| Тип | Количество сеток | Атрибуция | Проверено? |
|---|---|---|---|
| Квази-магический судоку | 248,832 | Джонс, Перкинс и Роуч[19] | да[нужна цитата] |
| Волшебное судоку | 5,971,968 | Stertenbrink[20] | да[нужна цитата] |
| Гиперкуб | 37,739,520 | Stertenbrink[21] | да[нужна цитата] |
| 3doku | 104,015,259,648 | Stertenbrink[22] | да[нужна цитата] |
| NRC Судоку | 6,337,174,388,428,800 | Брауэр[23] | да[нужна цитата] |
| Судоку X | 55,613,393,399,531,520 | Рассел[24] | да[нужна цитата] |
| Непересекающиеся группы | 201,105,135,151,764,480 | Рассел[25] | да[нужна цитата] |
Судоку с прямоугольными областями
В таблице размеры блоков соответствуют размерам регионов (например, 3 × 3 в обычном судоку). Столбец «Rel Err» показывает, как простое приближение[26] основанный на рассчитанном количестве полос (подробно описанном в разделах ниже), сравнивается с истинным подсчетом сетки: это заниженная оценка во всех случаях, оцененных до сих пор. Цифры для квадратных блочных сеток (п2 × п2) перечислены в (последовательность A107739 в OEIS), а числа для 2 × п блоки (2п × 2п сетки) перечислены в (последовательность A291187 в OEIS).
Похожий на Латинские квадраты, количество сеток судоку может быть уменьшенный отмечая, что существует взаимно однозначное соответствие с частично стандартизованной формой, в которой первый блок имеет канонические метки, а верхняя строка и крайний левый столбец сортируются (насколько позволяют правила, т.е. внутри блоков и сами стеки / ленты). Для сетки с блоков, каждая такая редуцированная сетка соответствует
| Размеры | Количество полных сеток | Стандартное восточное время. ошибка (Смотри ниже) | Доля | ||||
|---|---|---|---|---|---|---|---|
| Сетка | Блоки | Точный | Величина | Атрибуция | Проверено? | ||
| 4×4 | 2×2 | 288 | 2.8800×102 | разные[29] | да | −11.1% | 0.5×100 |
| 6×6 | 2×3 | 28,200,960 | 2.8201×107 | Петтерсен[30] | да[31] | −5.88% | 3.5×10−2 |
| 8×8 | 2×4 | 29,136,487,207,403,520 | 2.9136×1016 | Рассел[31] | да[32] | −1.91% | 2.7×10−4 |
| 9×9 | 3×3 | 6,670,903,752,021,072,936,960 | 6.6709×1021 | Stertenbrink[7] | да[9] | −0.207% | 1.2×10−6 |
| 10×10 | 2×5 | 1,903,816,047,972,624,930,994,913,280,000 | 1.9038×1030 | Петтерсен[33] | да[34] | −0.375% | 1.9×10−7 |
| 12×12 | 3×4 | 81,171,437,193,104,932,746,936,103,027,318,645,818,654,720,000 | 8.1171×1046 | Петтерсен / Сильвер[35] | Нет | −0.132%[35] | неизвестный |
| 12×12 | 2×6 | 38,296,278,920,738,107,863,746,324,732,012,492,486,187,417,600,000 | 3.8296×1049 | Петтерсен[36] | Нет | −0.238%[36] | неизвестный |
| 15×15 | 3×5 | неизвестный | стандартное восточное время.3.5086×1084 | Серебро[37] | Нет | н / д | неизвестный |
| 16×16 | 4×4 | неизвестный | стандартное восточное время.5.9584×1098 | Серебро[38] | Нет | н / д | неизвестный |
| 20×20 | 4×5 | неизвестный | стандартное восточное время.3.1764×10175 | Серебро[39] | Нет | н / д | неизвестный |
| 25×25 | 5×5 | неизвестный | стандартное восточное время.4.3648×10308 | Сильвер / Петтерсен[40] | Нет | н / д | неизвестный |
Решенная судоку останется в силе в соответствии с действиями преобразования, сохраняющие достоверность (см. также Джарвис[13]). Тщательно подсчитывая количество инвариантных сеток для каждого преобразования, можно вычислить количество существенно разных сеток судоку (см. Выше). Аналогичные методы были применены к сеткам судоку других размеров; результаты приведены в таблице ниже. Для решеток из квадратных блоков (последовательность A109741 в OEIS) преобразование транспонирования может быть включено или не включено (выделено курсивом ниже) в группу VPT (симметрия). Количество существенно разных сеток также можно оценить, разделив общее количество сеток (известных или оцененных) на размер группы VPT (которая легко вычисляется), что, по сути, предполагает, что количество автоморфных судоку незначительно. Цифры для 2 × п блоки (2п × 2п сетки) перечислены в (последовательность A291188 в OEIS).
| Размеры | Количество принципиально разных сеток | Размер группы ВПТ | Кол-во конн. классы (без перемаркировки) | Ссылка | |
|---|---|---|---|---|---|
| Сетка | Блоки | ||||
| 4×4 | 2×2 | 2 | 128 × 4! | [41][42] | |
| 4×4 | 2×2 | 3 | 64 × 4! | [41] | |
| 6×6 | 2×3 | 49 | 3,456 × 6! | 90 | Джарвис / Рассел[43], Петтерсен[41] |
| 8×8 | 2×4 | 1,673,187 | 4,423,368 × 8! | 400 | Рассел[44] , Петтерсен[41] |
| 9×9 | 3×3 | 5,472,730,538 | 3,359,232 × 9! | 275 | Джарвис / Рассел[13], Петтерсен[45][41] |
| 9×9 | 3×3 | 10,945,437,157 | 1,679,616 × 9! | 484 | Джарвис / Рассел[13], Петтерсен[45][41] |
| 10×10 | 2×5 | 4,743,933,602,050,718 | 110,592,000 × 10! | 1260 | Петтерсен / Рассел[46][47] |
| 16×16 | 4×4 | стандартное восточное время. 2.2458×1071 | (4!)10 × 2 × 16! | (оценка объяснена в тексте)[48] | |
Метод оценки
Метод Кевина Килфойла[49] (обобщено Петтерсеном[26]) можно использовать для оценки количества завершенных сеток с использованием количества возможных завершенных полос и стеков. Метод утверждает, что ограничения строк и столбцов судоку в первом приближении условно независимый учитывая ограничение коробки. Это дает Формула килфойла-серебра-петтерсена:[26]
куда это количество способов заполнения р×RC группа р горизонтально смежный р×C коробки (эквивалентно, это количество способов заполнения RC×C стопка C вертикально смежный р×C коробки), а знаменатель (RC)!RC - это количество способов заполнить сетку, удовлетворяя только ограничения блока.
Как пояснил Петтерсен: «Вот как: пусть Икс быть пространством -сетки, построенные легальными группами судоку, но без учета того, соответствуют ли столбцы правилам судоку. Размер Икс является . Пусть также Y быть набором сеток, построенных из разрешенных стеков без внимания к строкам, #Y затем . Сетки nxm-судоку являются пересечением Икс и Y. Случайный и идентичны в данном ящике с вероятностью , и в предположении, что эти вероятности независимы для каждого ящика, мы приходим к оценке выше ".[26]
Эта оценка оказалась точной примерно до 0,2% для классической сетки 9 × 9 и в пределах 1% для более крупных сеток, для которых известны точные значения (см. Таблицу выше).
Количество полос
Точные формулы для количества возможных полос в заполненной сетке судоку с размерами блоков р×C известны:
| Размеры | Количество полос | Атрибуция | Проверено? | |
|---|---|---|---|---|
| Группа | Блоки | |||
| 2×2C | 2×C | (очевидный результат) | да[нужна цитата] | |
| 3×3C | 3×C | где суммирование известно как Cth Номер Franel (последовательность A000172 в OEIS) | Петтерсен[30] | да[нужна цитата] |
| 4×4C | 4×C |
Внешнее суммирование соответствует разделению полосы на две «поддиапазоны» по 2 блока каждая; цифры а, б и c описывают разбиение и должны совпадать для обоих поддиапазонов, поэтому слагаемое можно возвести в квадрат. Переменные разделения описываются как: "а - это количество символов в строке 1 и 2 в первых ячейках (то есть символы, которые находятся либо в строке 1 в поле 1 и строке 2 в поле 2 ИЛИ в строке 1 в поле 2 и строке 2 в поле 1). Тогда это также будет количество символов в строках 3 и 4 в первых двух ячейках, а также количество символов в строках 1 и 2 в двух последних ячейках и количество символов в строках 3 и 4 в первые две коробки. б - количество символов в строках 1 и 3 в первых двух полях вместе с другими комбинациями, как для переменной а. c - количество символов в строках 1 и 4 в первых двух полях ».[50] Внутреннее суммирование подсчитывает количество поддиапазонов для данного а,б,c спецификация: «Среди а символы, которые лежат в строках 1 и 2 в ячейках 1 и 2, k12 подсчитывает, сколько из них находится в строке 1 в поле 1 (и, следовательно, также в строке 2 в поле 2). В общем, для я<j, среди символов в строке я и j в первых двух полях, kij говорит, сколько из них в ряду я в поле 1 и строке j в рамке 2. "[50] | Петтерсен[51] | да[52] |
Ниже перечислены несколько известных количеств полос. Алгоритм Петерсена,[53] как реализовано и улучшено Silver,[54] разбивает полосу на поддиапазоны, которые затем группируются в классы эквивалентности; в настоящее время это самый быстрый из известных методов точной оценки этих бR, C.
| Размеры | Количество полос | Атрибуция | Проверено? | |
|---|---|---|---|---|
| Группа | Блоки | |||
| 3×6 | 3×2 | 6! × 2!6 × 10 = 460800 | Петтерсен (формула) | |
| 3×9 | 3×3 | 9! × 3!6 × 56 = 9! × 2612736 = 948109639680 ≈ 9.4811×1011 (44 класса эквивалентности[10][55]) | Разные[10][30] | |
| 3×12 | 3×4 | 12! × 4!6 × 346 = 31672366418991513600 ≈ 3.1672×1019 | Stertenbrink[нужна цитата] | да[50] |
| 3×15 | 3×5 | 15! × 5!6 × 2252 ≈ 8.7934×1027 | Петтерсен (формула)[37] | |
| (большие значения 3 × C можно легко вычислить, используя формулу, приведенную выше) | ||||
| 4×8 | 4×2 | 8! × 2!12 × 5016 = 828396011520 ≈ 8.2840×1011 | [нужна цитата] | |
| 4×12 | 4×3 | 12! × 3!12 × 2180544 = 2273614462643364849254400 ≈ 2.2736×1024 | Петтерсен[30] | да[50] |
| 4×16 | 4×4 | 16! × 4!12 × 1273431960 ≈ 9.7304×1038 | Серебро[38][56] | да[нужна цитата] |
| 4×20 | 4×5 | 20! × 5!12 × 879491145024 ≈ 1.9078×1055 | Рассел[56] | да[нужна цитата] |
| 4×24 | 4×6 | 24! × 6!12 × 677542845061056 ≈ 8.1589×1072 | Рассел[56] | да[нужна цитата] |
| 4×28 | 4×7 | 28! × 7!12 × 563690747238465024 ≈ 4.6169×1091 | Рассел[56] | да[нужна цитата] |
| (расчеты до 4 × 100 были выполнены Silver,[57] но не указаны здесь) | ||||
| 5×10 | 5×2 | 10! × 2!20 × 364867776 ≈ 1.3883×1021 (355 классов эквивалентности[33]) | [нужна цитата] | Нет |
| 5×15 | 5×3 | 15! × 3!20 × 324408987992064 ≈ 1.5510×1042 | Серебро[39] | датот же автор, другой метод |
| 5×20 | 5×4 | 20! × 4!20 × 518910423730214314176 ≈ 5.0751×1066 | Серебро[39] | датот же автор, другой метод |
| 5×25 | 5×5 | 25! × 5!20 × 1165037550432885119709241344 ≈ 6.9280×1093 | Петтерсен / Сильвер[40] | Нет |
| 5×30 | 5×6 | 30! × 6!20 × 3261734691836217181002772823310336 ≈ 1.2127×10123 | Петтерсен / Сильвер[40] | Нет |
| 5×35 | 5×7 | 35! × 7!20 × 10664509989209199533282539525535793414144 ≈ 1.2325×10154 | Петтерсен / Сильвер[58] | Нет |
| 5×40 | 5×8 | 40! × 8!20 × 39119312409010825966116046645368393936122855616 ≈ 4.1157×10186 | Петтерсен / Сильвер[54] | Нет |
| 5×45 | 5×9 | 45! × 9!20 × 156805448016006165940259131378329076911634037242834944 ≈ 2.9406×10220 | Петтерсен / Сильвер[нужна цитата] | Нет |
| 5×50 | 5×10 | 50! × 10!20 × 674431748701227492664421138490224315931126734765581948747776 ≈ 3.2157×10255 | Петтерсен / Сильвер[нужна цитата] | Нет |
| 6×12 | 6×2 | 12! × 2!30 × 9480675056071680 = 4876139207527966044188061990912000 ≈ 4.8761×1033 | Петтерсен[59] | Нет |
Загадки
Минимальное количество данностей
Обычные судоку (правильный головоломки) имеют уникальное решение. А минимальный Судоку - это судоку, от которого невозможно избавиться, оставив его правильным судоку. Разные минимальные судоку могут иметь разное количество подсказок. В этом разделе обсуждается минимальное количество заданий для правильных головоломок.
Обычные судоку
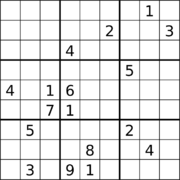
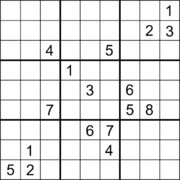 Судоку с 17 подсказками и диагональной симметрией.[60] | 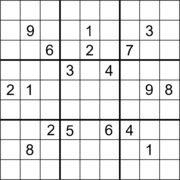 Судоку с 18 подсказками и ортогональной симметрией.[61] |
 Судоку с 19 подсказками и двусторонней ортогональной симметрией.[63] |
Было найдено множество судоку с 17 подсказками, хотя найти их - нетривиальная задача.[64][65] В статье Гэри Макгуайра, Бастиана Тугеманна и Жиля Сиварио, опубликованной 1 января 2012 года, объясняется, как с помощью исчерпывающего компьютерного поиска было доказано, что минимальное количество подсказок в любом правильном судоку составляет 17,[66][67][12] и это было независимо подтверждено в сентябре 2013 года.[68] Эд Рассел предложил несколько головоломок с 17 ключами и диагональной симметрией после поиска преобразований эквивалентности Гордон РойлБаза данных из 17 загадок.[69][60] Головоломки судоку с 18 подсказками были найдены с вращательной симметрией 180 °, а другие - с ортогональной симметрией, хотя неизвестно, является ли это количество подсказок минимальным в любом случае.[61] Головоломки судоку с 19 подсказками были найдены с двусторонней ортогональной симметрией, и снова неизвестно, является ли это количество подсказок минимальным для этого случая.[63]
Судоку с 24 подсказками, двугранный симметрия (симметрия относительно обеих ортогональных осей, симметрия вращения 90 °, симметрия вращения 180 ° и диагональная симметрия), как известно, существует, а также автоморфный. Опять же, здесь неизвестно, является ли это количество подсказок минимальным для этого класса судоку.[62][70] Считается, что наименьшее количество подсказок в судоку с двусторонней диагональной симметрией - 18, и по крайней мере в одном случае такое судоку также демонстрирует автоморфизм.
Среди 5 472 730 538 Принципиально разные сетки решений, только 4 не имеют головоломки с 20 подсказками - у этих 4 сеток есть головоломка с 21 подсказкой.[71]
Судоку других размеров
- Судоку 4 × 4 (2 × 2): наименьшее количество подсказок в любом судоку 4 × 4 - 4, из которых 13 неэквивалентных головоломок. (Общее количество неэквивалентных минимальных судоку такого размера - 36).[72]
- 6 × 6 (2 × 3) Судоку: наименьшее количество подсказок - 8.[73]
- Судоку 8 × 8 (2 × 4): наименьшее количество подсказок - 14.[73]
- 10 × 10 (2 × 5) Судоку: создана как минимум одна головоломка с 22 подсказками.[74] Неизвестно, насколько это возможно.
- 12 × 12 (2 × 6) Судоку: была создана по крайней мере одна головоломка с 32 подсказками.[74] Неизвестно, насколько это возможно.
- 12 × 12 (3 × 4) Судоку: была создана по крайней мере одна головоломка с 30 подсказками.[74] Неизвестно, насколько это возможно.
- 15 × 15 (3 × 5) Судоку: была создана по крайней мере одна головоломка с 48 подсказками.[74] Неизвестно, насколько это возможно.
- 16 × 16 (4 × 4) Судоку: была создана по крайней мере одна головоломка с 55 подсказками.[74] Неизвестно, насколько это возможно.
- 25 × 25 (5 × 5) Судоку: создана головоломка со 151 подсказкой.[75][нужна цитата] Неизвестно, насколько это возможно.
Судоку с дополнительными ограничениями
Дополнительные ограничения (здесь, на судоку 3 × 3) приводят к меньшему минимальному количеству подсказок.
- Непересекающиеся группы: несколько головоломок с 12 ключами[76] были продемонстрированы Гленном Фаулером. Позже были найдены 11 загадок. Неизвестно, насколько это возможно.
- Гиперкуб: различные головоломки с 8 ключами[77] были продемонстрированы Гюнтером Стертенбринком. Это лучшее из возможных.
- Волшебное судоку: пример из 7 подсказок[78] был предоставлен Guenter Stertenbrink. Неизвестно, насколько это возможно.
- Судоку против рыцарей: 9 подсказок[79] предоставлен пользователем Reddit u / wand125. Есть подозрение, что это лучшее из возможных.
- Судоку X: список из 7193 головоломок с 12 подсказками[80] Собран Руудом ван дер Верфом. Неизвестно, насколько это возможно.
- Судоку NRC: пример из 11 подсказок[23] предоставлен Андрисом Брауэром. Неизвестно, насколько это возможно.
- 2-квази-магическое судоку: пример из 4 подсказок[81] предоставлен Тони Форбсом. Есть подозрение, что это лучшее из возможных.
Судоку с неправильными участками
"Ду-сум-ой"[82] (также известный как "место числа геометрических фигур") головоломки заменяют 3 × 3 (или р×C) области судоку неправильной формы фиксированного размера. Боб Харрис доказал[83] что всегда можно создать (N - 1) -ключ дю-сум-ох на N×N grid и построил несколько примеров. Йохан де Руйтер доказал[84] это для любого N> 3 существуют мозаики полимино, которые нельзя превратить в головоломку судоку с N неправильные формы размера N.
Сумма номер место («Убийственная судоку»)
В общем месте (Samunampure) области имеют неправильную форму и разные размеры. Применяются обычные ограничения отсутствия повторяющихся значений в любой строке, столбце или области. Подсказки даются как суммы значений внутри регионов (например, 4-ячеечная область с суммой 10 должна состоять из значений 1,2,3,4 в некотором порядке). Минимальное количество ключей к разгадке Самунампура не известно и даже не предполагалось. Вариант на веб-сайте Миюки Мисавы[85] заменяет суммы отношениями: ключи - символы =, < и > показывает относительные значения (некоторых, но не всех) сумм по соседним регионам. Она демонстрирует пример всего с восемью отношениями. Неизвестно, насколько это возможно.
Максимальное количество данных
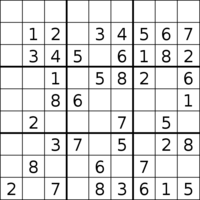
Большинство подсказок для минимальный Считается, что судоку насчитывается 40, из которых известны только два. Если какая-либо подсказка будет удалена из любого из этих судоку, головоломка будет иметь более одного решения (и, следовательно, не будет правильным судоку). В процессе поиска этих судоку были внесены в каталог другие головоломки с высокой подсказкой, в том числе более 6 500 000 000 минимальных головоломок с 36 подсказками. Также было найдено около 2600 минимальных судоку с 39 подсказками.[86]
Если отказаться от требования уникальности решения, известно, что существуют минимальные псевдопазлы с 41 подсказкой, но они могут быть решены в несколько сеток решений. Удаление любой подсказки увеличивает количество завершений, и с этой точки зрения ни одна из 41 подсказки не является лишней. Когда сетка заполнена данными чуть более чем на половину (41 ячейка из 81), уникальность ограничения решения по-прежнему доминирует над минимальность ограничение.[87]
Для наиболее подсказки возможны в судоку, пока еще нет что дает уникальное решение, это в четыре раза меньше полной сетки (77). Если отсутствуют два экземпляра двух чисел в каждом, а ячейки, которые они должны занимать, являются углами ортогонального прямоугольника, и ровно две из этих ячеек находятся в одной области, есть два способа сложения последних цифр (два решения).
Количество минимальных головоломок
Количество минимальных судоку (судоку, в котором нельзя удалить ключ без потери уникальности решения) точно не известно. Однако статистические методы в сочетании с генератором («Беспристрастная статистика CSP - генератор контролируемого смещения»),[88] показывают, что есть приблизительно (с относительной погрешностью 0,065%):
- 3.10 × 1037 минимальные головоломки,
- 2.55 × 1025 неэквивалентные минимальные головоломки.
Другие авторы использовали более быстрые методы и рассчитали дополнительную точную статистику распределения.[89]
Ограничения геометрии подсказки
Было высказано предположение, что ни одна правильная судоку не может иметь подсказок, ограниченных диапазоном позиций в приведенном выше шаблоне (первое изображение).[90] Самая большая прямоугольная ортогональная «дыра» (область без подсказок) в правильном судоку считается прямоугольником из 30 ячеек (прямоугольная область 5 × 6).[91][92] Одним из примеров является судоку с 22 подсказками (второе изображение). Считается, что наибольшее общее количество пустых групп (строк, столбцов и ящиков) в судоку составляет девять. Одним из примеров является судоку с 3 пустыми строками, 3 пустыми столбцами и 3 пустыми полями (третье изображение).[93][94]
Автоморфный судоку
Сетка судоку является автоморфной, если ее можно преобразовать таким образом, чтобы вернуться к исходной сетке, когда то же преобразование не привело бы к исходной сетке. Одним из примеров автоморфной сетки может быть сетка, которую можно повернуть на 180 градусов, в результате чего получится новая сетка, в которой новые значения ячеек являются перестановкой исходной сетки. Автоморфные судоку - это головоломки судоку, которые решаются в автоморфную сетку. Ниже показаны два примера автоморфных судоку и автоморфная сетка.
 Автоморфная судоку с 18 подсказками (двусторонняя диагональная симметрия)[95] |  Автоморфная судоку с 24 подсказками (двусторонняя диагональная симметрия и трансляционная симметрия)[96] |
| Авто- морфизмы | Кол-во сеток | Авто- морфизмы | Нет. сетки |
|---|---|---|---|
| 1 | 5472170387 | 18 | 85 |
| 2 | 548449 | 27 | 2 |
| 3 | 7336 | 36 | 15 |
| 4 | 2826 | 54 | 11 |
| 6 | 1257 | 72 | 2 |
| 8 | 29 | 108 | 3 |
| 9 | 42 | 162 | 1 |
| 12 | 92 | 648 | 1 |
В первых двух примерах обратите внимание, что если судоку повернуть на 180 градусов и пометить подсказки с перестановкой (123456789) -> (987654321), он вернется к тому же судоку. Другими словами, эти судоку обладают тем свойством, что каждая пара ключей (a, b), вращающихся на 180 градусов, подчиняется правилу (a) + (b) = 10.
Поскольку эти судоку автоморфны, их решетки также автоморфны. Кроме того, каждая решенная ячейка имеет симметричного партнера, который решается с помощью той же техники (и пара принимает форму a + b = 10). Обратите внимание, что во втором примере судоку также показывает переводной (или повторение) симметрии; подсказки сгруппированы в группы, причем подсказки в каждой группе упорядочены последовательно (то есть n, n + 1, n + 2 и n + 3).
Третье изображение - это Самый канонический сетка решения.[97] Эта сетка имеет 648 автоморфизмов и вносит вклад во все ~6.67×1021 решетки в 1/648 раз по сравнению с любой неавтоморфной сеткой.
В этих примерах автоморфизмы легко идентифицировать, но в целом автоморфизм не всегда очевиден. В таблице справа показано количество существенно различных сеток решений судоку для всех существующих автоморфизмов.[11]
Детали перечисления различных сеток (9 × 9)
Методика подсчета, основанная на группа поколения был разработан, что требует значительно меньших вычислительных затрат. Стратегия начинается с анализа перестановки верхней полосы, используемой в действительных решениях. Однажды Band1 симметрии и класс эквивалентности для частных решений строятся пополнения двух нижних полос и подсчитываются для каждого класса эквивалентности.
Подсчет перестановок верхней полосы
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Алгоритм Band1 работает следующим образом:
- Выберите каноническую маркировку цифр, присвоив значения B1 (см. Сетку), и вычислите остальные перестановки Band1 относительно B1.
- Вычислить перестановки B2 с помощью разделение значения ячейки B1 по строке B2 тройняшки. Из комбинаций триплетов вычисляют перестановки B2. Есть k = 0..3 способов выбрать:
- B1 r11 значения для B2 r22, остальные должны идти на r16,
- B1 r12 значения для B2 r23, остальные должны идти в r16,
- B1 r13 значения для B2 r21, остальные должны идти на r16, т.е.
(Это выражение можно обобщить на любой р× 3 вариант коробчатой ленты. (Петтерсен[30]). Таким образом, B2 дает 56 × 63 перестановки.
- Выбор триплетов B3 построчно определяется тройками строк B1 B2. B3 всегда вносит 63 перестановки.
Перестановки для Band1 следующие: 9! × 56 × 66 = 9! × 2612736 ≈ 9.48×1011.
Детали перестановки Band1
|
|
|
Перестановки B1 - это количество способов переименовать 9 цифр, 9! = 362880. Подсчет перестановок для B2 сложнее, потому что выбор для B2 зависит от значений в B1. (Это наглядное представление приведенного выше выражения.) Условное вычисление требует ветви (подвычисления) для каждой альтернативы. К счастью, для верхней тройки B2 (r21) всего 4 случая: она содержит 0, 1, 2 или 3 цифры из тройки средней строки B1 (r12). После того, как этот выбор верхнего ряда B2 сделан, остальные комбинации B2 фиксируются. Метки тройки строк Band1 показаны справа.
(Примечание: условные комбинации становятся все более сложными по мере того, как вычисления проходят через сетку. В этот момент влияние минимально.)
|
|
|
Случай 0: без перекрытия. Выбор тройки может быть определен путем исключения.
- r21 не может быть r11 или r12, поэтому должно быть = r13; r31 должно быть = r12 и т. д.
Диаграмма Случай 0 показывает эту конфигурацию, где розовые ячейки представляют собой значения триплета, которые могут быть расположены в любом порядке внутри триплета. Каждая триплет имеет 3! = 6 перестановок. 6 троек вносят 66 перестановки.
Случай 3: совпадение трех цифр: тройка r21 = r12. Применяется та же логика, что и в случае 0, но с другим использованием триплетов. Тройной r22 должен быть = r13 и т. Д. Количество перестановок снова равно 66 (Фельгенгауэр / Джарвис).[10] Случаи 0 и 3 назовите чистый матч дело.
|
|
|
Случай 1: 1 Соответствует r21 от r12
На диаграмме случая 1 ячейки B1 показывают канонические значения, которые имеют цветовую кодировку, чтобы показать их построчное распределение в триплетах B2. Цвета отражают распределение, но не местоположение или ценности. Для этого случая: тройка верхней строки B2 (r21) имеет значение 1 из средней тройки B1, теперь можно вывести другие цвета. Например. раскраска тройки нижней строки B2 (r23) принудительно раскрашена r21: другие 2 средних значения B1 должны идти вниз и т. д. Введите количество вариантов B2 для каждого цвета, 3..1, начиная с верхнего левого угла. Цветовое кодирование B3 опущено, поскольку варианты B3 построчно определяются B1, B2. B3 всегда вносит 3! перестановок на тройку строк, или 63 для блока.
Для B2 значения триплета могут появляться в любой позиции, поэтому 3! коэффициент перестановки по-прежнему применяется для каждого триплета. Однако, поскольку некоторые из значений были парными относительно их происхождения, использование необработанных подсчетов опций привело бы к завышению количества перестановок из-за взаимозаменяемости в паре. Количество опций необходимо разделить на переставленный размер их группы (2), здесь 2! = 2 (см. ) Пара в каждой строке отменяет двойки для подсчета варианта B2, оставляя вклад B2 в размере 33 × 63. Комбинированный вклад B2 × B3 равен 33 × 66.
|
|
|
Случай 2: 2 совпадения для r21 от r12. Применяется та же логика, что и в случае 1, но с обратным группированием столбцов с помощью параметра B2. Случай 3 также способствует 33×66 перестановки.
Суммирование 4 случаев для Band1 B1..B3 дает9! × 2 × (33 + 1) × 66 = 9! 56 × 66 перестановки.
Band1 симметрии и классы эквивалентности
Симметрии используются для уменьшения вычислительных затрат на перечисление перестановок Band1. А симметрия - это операция, сохраняющая качество объекта. Для сетки судоку симметрия - это преобразование, результатом которого также является действительная сетка. Для верхней полосы независимо применяются следующие симметрии:
- Значения блока B1 можно переименовать, получив 9! перестановки
- Блоки B1..3 можно менять местами с 3! = 6 перестановками
- Строки 1..3 можно менять местами, 3! = 6 перестановок.
- В каждом блоке 3 столбца можно поменять местами, что дает 3!3 = 63 перестановки.
Вместе симметрии дают 9! × 65 = 362880 × 7776 эквивалентных перестановок для каждого решения Band1.
Симметрия определяет отношение эквивалентности, здесь между решениями и перегородки решения в набор классы эквивалентности. Симметрии строки, столбца и блока Band1 делят перестановок в (не менее) 336 (56 × 6) классов эквивалентности с (до) 65 перестановок в каждом и 9! перемаркировка перестановок для каждого класса. (Мин Макс применяются предостережения, поскольку некоторые перестановки могут не давать отдельных элементов из-за перемаркировки.)
Поскольку решение для любого члена класса эквивалентности может быть сгенерировано из решения любого другого члена, нам нужно только перечислить решения для одного члена, чтобы перечислить все решения по всем классам. Позволять
- sb: быть допустимой перестановкой верхней полосы
- Sb = [sb]: быть классом эквивалентности относительно sb и некоторого отношение эквивалентности
- Sb.z = | Sb | : размер Sb, количество элементов (перестановок) sb в [sb]
- Sb.n: число завершений Band2,3 для (любого) sb в Sb
- {Sb}: множество всех классов эквивалентности Sb относительно отношение эквивалентности
- {Sb} .z = | {Sb} | : быть количеством классов эквивалентности
Общее количество решений N затем:
- N = Sb.z × Сб.н
Решение и подсчет перестановочной симметрии
Симметрии Band1 (см. Выше) равны симметрии перестановки решений определено так, что переставленное решение также является решением. Для перечисления решений считая симметрию для завершения сетки можно использовать для определения классов эквивалентности полос, которые дают минимальное количество классов.
Считая симметрию разбивает допустимые перестановки Band1 на классы, которые накладывают те же ограничения завершения на нижние диапазоны; все участники группы считая симметрию Класс эквивалентности должен иметь одинаковое количество завершений сетки, поскольку ограничения завершения эквивалентны. Ограничения симметрии подсчета идентифицируются тройками столбцов Band1 (набор значений столбца, без подразумеваемого порядка элементов). Используя симметрию подсчета полос, минимальный набор из 44 классов эквивалентности[55] был основан.
|
|
|
Следующая последовательность демонстрирует сопоставление конфигурации полосы с классом эквивалентности счетной симметрии. Начните с допустимой конфигурации диапазона (1). Создавайте тройки столбцов, упорядочивая значения столбцов в каждом столбце. Это недопустимый диапазон для судоку, но он накладывает те же ограничения на нижние диапазоны, что и в примере (2). Создайте идентификатор класса эквивалентности из значений триплета столбцов B2, B3. Используйте перестановки столбцов и прямоугольников, чтобы получить наименьший лексикографический идентификатор. На последнем рисунке показан порядок столбцов и прямоугольников для идентификатора: 124 369 578 138 267 459. Все перестановки Band1 с этим идентификатором симметрии подсчета будут иметь такое же количество завершений сетки, что и исходный пример. Расширение этого процесса может быть использовано для создания максимально возможного симметрия подсчета полос классы эквивалентности (3).
Обратите внимание, что в то время как тройки столбцов используются для создания и идентификации классов эквивалентности, сами члены класса являются допустимыми перестановками Band1: размер класса (Sb.z) отражает перестановки тройки столбцов, совместимые с Одно правило требования к решению. Считая симметрию является свойством завершения и применяется только к частичной сетке (полосе или стеку). Симметрия решения для сохранения решений может применяться как к частичным сеткам (полосы, стопки), так и к полным сеткам. Наконец, обратите внимание, считая симметрию является более ограничительным, чем простое числовое равенство числа завершения: две (разные) полосы принадлежат одному считая симметрию класс эквивалентности, только если они налагают эквивалентные ограничения завершения.
Детали редукции Band 1
Симметрии группируют похожие объекты в классы эквивалентности. Необходимо различать два числа для классов эквивалентности и симметрии полос, как здесь используется, третье:
- количество классов эквивалентности ({Sb} .n).
- то мощность, размер или количество элементов в классе эквивалентности, которые могут варьироваться в зависимости от класса (Sb.z)
- количество пополнений Band2,3, совместимых с членом класса эквивалентности Band1 (Sb.n)
Группа1 (65) симметрии делят (56 × 66) Band1 допустимые перестановки в (не менее) 336 (56 × 6) классов эквивалентности с (до) перестановки каждый. не меньше чем и вплоть до предостережения необходимы, так как некоторые комбинации преобразований могут не дать отличных результатов, когда требуется перемаркировка (см. ниже). Следовательно, некоторые классы эквивалентности могут содержать менее 65 отдельные перестановки и теоретическое минимальное количество классов не могут быть достигнуты.
Каждая из допустимых перестановок Band1 может быть расширена (завершена) в определенное количество решений с перестановками Band2,3. В силу своей схожести каждый член класса эквивалентности будет иметь одинаковое количество завершений. Следовательно, нам нужно только построить решения для одного члена каждого класса эквивалентности, а затем умножить количество решений на размер класса эквивалентности. Нам все еще остается задача определить и рассчитать размер каждого класса эквивалентности. Дальнейший прогресс требует ловкого применения вычислительных методов для каталогизации (классификации и подсчета) перестановок в классы эквивалентности.
Фельгенгауэр / Джарвис[10] каталогизировали перестановки Band1, используя лексикографически упорядоченный Идентификаторы на основе упорядоченных цифр из блоков B2,3. Блок 1 использует каноническое присвоение цифр и не требуется для уникального идентификатора. Для идентификации и связывания класса эквивалентности используется самый низкий идентификатор в классе.
Применение (2 × 62) Перестановки симметрии B2,3 дают 36288 (28 × 64) классов эквивалентности, каждый размером 72. Поскольку размер фиксирован, вычислению нужно только найти 36288 идентификаторов классов эквивалентности. (Примечание: в этом случае для любой перестановки Band1 применение этих перестановок для достижения наименьшего идентификатора обеспечивает индекс для соответствующего класса эквивалентности.)
Применение остальных симметрий блоков, столбцов и строк обеспечило дальнейшее сокращение, т. Е. Выделение 36288 идентификаторов в меньшее количество более крупных классов эквивалентности. Когда каноническая маркировка B1 теряется в результате преобразования, результат изменяется на каноническое использование B1 и затем внесены в каталог под этим идентификатором. При таком подходе было получено 416 классов эквивалентности, что несколько менее эффективно, чем теоретический минимальный предел в 336 для полного сокращения. Применение считая симметрию шаблоны для дубликат пары цифр удалось снизить до 174, а затем до 71 класса эквивалентности. Введение классов эквивалентности на основе симметрия подсчета полос (вслед за Фельгенгауэром / Джарвисом Расселом[55]) сократил классы эквивалентности до минимального набора из 44 порождающих.
Разнообразие ~2.6×106, 56×66 Перестановки Band1 могут быть сведены к набору из 44 классов эквивалентности Band1. Каждый из 44 классов эквивалентности может быть расширен до миллионов отдельных полных решений, но все пространство решений имеет общий источник в этих 44. 44 класса эквивалентности также играют центральную роль в других подходах к перечислению, и предположения вернутся к характеристики 44 классов, когда свойства головоломки будут исследованы позже.
Завершение диапазона 2–3 и результаты
Перечисление решений судоку разбивается на этап начальной настройки, а затем - на два вложенных цикла. Первоначально все допустимые перестановки Band1 сгруппированы в классы эквивалентности, каждый из которых накладывает общее ограничение на завершение Band2,3. Для каждого из классов эквивалентности Band1 необходимо перечислить все возможные решения Band2,3. Внешний цикл Band1 выполняет итерацию по 44 классам эквивалентности. Во внутреннем цикле обнаруживаются и подсчитываются все завершения нижней полосы для каждого класса эквивалентности Band1.
Вычисления, необходимые для поиска решения нижней полосы, можно минимизировать с помощью того же типа приложения симметрии, что и для Band1. Их 6! (720) перестановки для 6 значений в столбце 1 Band2,3. Применение перестановок нижней полосы (2) и строки внутри полосы (6 × 6) создает 10 классов эквивалентности размера 72. На этом этапе, завершая 10 наборов решений для оставшихся 48 ячеек с рекурсивным спуском, возврат алгоритм возможен с ПК класса 2 ГГц, поэтому дальнейшее упрощение не требуется для проведения подсчета. Используя этот подход, было показано, что количество способов заполнения пустой сетки судоку составляет 6 670 903 752 021 072 936 960 (6.67×1021).[10]
Результат, как подтвердил Рассел,[55] также содержит распределение количества решений для 44 классов эквивалентности. Перечисленные значения приведены до применения 9! фактор для маркировки и два 72 фактора (722 = 5184) для каждой из перестановок Stack 2,3 и Band2,3. Число завершений для каждого класса постоянно составляет порядка 100000000, в то время как количество перестановок Band1, охватываемых каждым классом, варьируется от 4 до 3240. В этом широком диапазоне размеров явно есть два кластера. Ранжированные по размеру, нижние 33 класса в среднем составляют ~ 400 перестановок на класс, а верхние 11 - ~ 2100. Несоответствие в согласованности между распределениями по размеру и количеству завершенных или разделение на два кластера по размеру еще предстоит изучить.
Смотрите также
- Судоку - основная статья
- Алгоритмы решения судоку
- Глоссарий судоку
- Комбинаторный взрыв (со сводкой по сетке судоку по сравнению с латинскими квадратами)
- Варианты судоку
- Танцы Links
- Коды Судоку
Рекомендации
- ^ Линь, Кех Ин (2004), «Число судоку», Журнал развлекательной математики, 33 (2): 120–24.
- ^ «Основные термины: О форуме новых игроков в судоку». Forum.enjoysudoku.com. 16 мая 2006 г.. Получено 20 октября 2013.
- ^ Бертье, Дени (ноябрь 2007 г.). Скрытая логика судоку (Вторая, переработанная и дополненная ред.). Lulu.com. ISBN 978-1-84799-214-7. Получено 21 ноября 2017.
- ^ «NP Complete - Судоку» (PDF). Imai.is.su-tokyo.ac.jp. Получено 20 октября 2013.
- ^ а б Льюис, Р. Руководство по раскраске графиков: алгоритмы и приложения. Издательство Springer International, 2015.
- ^ а б де Руйтер, Йохан (15 марта 2010 г.). «О пазлах судоку и связанных темах (диплом бакалавра)» (PDF). Лейденский институт передовых компьютерных наук (LIACS).
- ^ а б QSCGZ (Guenter Stertenbrink) (21 сентября 2003 г.). "комбинаторный вопрос на 9х9 (рек. пазлы)". Google Discussiegroepen. Получено 20 октября 2013.
- ^ Рассел, Эд (1 февраля 2008 г.). "6670903752021072936960 - это старая шляпа". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c Джарвис, Фрейзер (2 февраля 2008 г.). "Проблемы с подсчетом судоку". Домашняя страница Фрейзера Джарвиса. Университет Шеффилда. Получено 20 октября 2013.
- ^ а б c d е ж Фельгенгауэр, Бертрам; Джарвис, Фрейзер (20 июня 2005 г.), Перечисление возможных сеток судоку (PDF).
- ^ а б c d Фаулер, Гленн (15 февраля 2007 г.). «Количество автоморфизмов для любой сетки». Форум новых игроков в судоку. Получено 29 апреля 2017.
- ^ а б Дж. Макгуайр, Б. Тугеманн, Дж. Сиварио. «Не существует судоку с 16 ключами: решение проблемы с минимальным количеством подсказок в судоку». Arxiv.org.
- ^ а б c d е ж грамм час я Эд Рассел и Фрейзер Джарвис (7 сентября 2005 г.). «Существует 5472730538 существенно разных решеток судоку ... и группа симметрии судоку». Домашняя страница Фрейзера Джарвиса. Университет Шеффилда. Получено 20 октября 2013.
- ^ Эд Рассел, Фрейзер Джарвис (25 января 2006 г.). «Математика судоку II» (PDF).
- ^ а б c одиннадцать (25 декабря 2008 г.). "О группе симметрии судоку Реда Эда". Форум новых игроков в судоку. Получено 13 июля 2020.
- ^ Рассел (24 января 2009 г.). «Re: О группе симметрий судоку Реда Эда (стр. 8) [список групп автоморфизмов]». Форум новых игроков в судоку. Получено 19 октября 2020.
- ^ Рассел (6 февраля 2009 г.). «Re: О группе симметрий судоку Реда Эда (стр. 13) [пересмотренный список групп автоморфизмов]». Форум новых игроков в судоку. Получено 19 октября 2020.
- ^ Рассел (14 февраля 2009 г.). «Re: О группе симметрий судоку Реда Эда (стр. 14) [структуры группы автоморфизмов]». Форум новых игроков в судоку. Получено 19 октября 2020.
- ^ Джонс, Сиан К .; Перкинс, Стефани; Роуч, Пол А. (6 июля 2011 г.). «Свойства, изоморфизмы и перечисление 2-квазимагических сеток судоку». Дискретная математика. 311 (13): 1098–1110. Дои:10.1016 / j.disc.2010.09.026.
- ^ "Программисты судоку :: Просмотр темы - Количество" волшебных судоку "(и случайная генерация)". Setbb.com. Архивировано из оригинал 6 февраля 2012 г.. Получено 20 октября 2013.
- ^ «Математика Су-Доку: Общие - стр. 27». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «Математика Су-Доку: Общие - стр. 27». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ а б «НРК Судокус». Homepages.cwi.nl. Получено 20 октября 2013.
- ^ «Вызов всех экспертов по судоку: Общие». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «Математика Су-Доку: Общие - Страница 13». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ а б c d Петтерсен, Кьелл (12 декабря 2005 г.). «Re: оценка для 4x4 [формула оценки KSP]». Форум новых игроков в судоку. forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ Петтерсен (15 апреля 2006 г.). «Счет судоку 4x3 - надежность (стр. 2)». Форум новых игроков в судоку. Получено 3 октября 2020.
- ^ Джонс, Перкинс, Роуч (май 2014 г.). «О количестве сеток судоку». Журнал комбинаторной математики и комбинаторных вычислений. Апрель: 94–95.CS1 maint: несколько имен: список авторов (связь)
- ^ Джефф (14 июня 2005 г.). «Математика судоку - могут ли смертные решить ее для квадрата 2x2? - Метод подсчета». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c d е Петтерсен (11 октября 2005 г.). «Математика Су-Доку - Некоторые мысли о более высоких судоку, чем 3x3 (стр. 28)». Форум новых игроков в судоку. Получено 2 октября 2020.
- ^ а б Красный Эд (16 октября 2005 г.). "Re: Математика Су-Доку (стр. 29)". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Петтерсен (17 октября 2005 г.). "Re: Математика Су-Доку (стр. 29)". Форум новых игроков в судоку. Получено 5 октября 2020.
- ^ а б Петтерсен (20 октября 2005 г.). «Re: Математика Су-Доку (стр. 29) [подсчет решетки судоку 5x2]». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Каспар, Матиас и Ларс (18 июля 2006 г.). "Математика Су-Доку (стр. 41) - 5x2 проверено?". Форум новых игроков в судоку. Получено 22 октября 2020.
- ^ а б Петтерсен (14 апреля 2006 г.). «Счет судоку 4x3 - Счет 4x3 завершен (стр. 2)». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б Петтерсен, Челл (14 ноября 2006 г.). «Re: счет 6x2 [сетка 6x2]». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б PatmaxDaddy (5 января 2006 г.). «Математика Су-Доку - оценка по сетке 5x3 (стр. 38)». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б PatmaxDaddy (12 декабря 2005 г.). «Математика Су-Доку - оценка для 4х4 (с. 36)». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c PatmaxDaddy (5 января 2006 г.). «Математика Су-Доку - результаты 5xC, группа 1». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c PatmaxDaddy (23 января 2006 г.). "Алгоритм подсчета полос RxC Sudoku - результаты диапазона 5xC". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c d е ж Петтерсен, Челл (8 июня 2006 г.). «Количество принципиально разных сеток судоку». Форум новых игроков в судоку. Получено 11 сентября 2020.
- ^ Арнольд, Элизабет; Филд, Ребекка; Лукас, Стивен; Таалман, Лаура (24 февраля 2013 г.). «Минимальные полные группы симметрий Сидоку». Журнал комбинаторной математики и комбинаторных вычислений. 87: 209–228. arXiv:1302.5949 - через arXiv.
- ^ Эд Рассел, Фрейзер Джарвис. «Есть 49 принципиально разных сеток судоку 2x3 ... и группа симметрии судоку 2x3». Домашняя страница Фрейзера Джарвиса. Университет Шеффилда. Получено 20 октября 2013.
- ^ Эд Рассел. «Существует 1673187 существенно разных сеток судоку 2x4 ... и группа симметрии судоку 2x4». Домашняя страница Фрейзера Джарвиса. Университет Шеффилда. Получено 20 октября 2013.
- ^ а б Петтерсен (5 ноября 2005 г.). "Математика Су-Доку (стр. 31)". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Кьелл Фредрик Петтерсен (по произведениям Эда Рассела). «Есть 4743933602050718 существенно разных сеток судоку 2x5 ... и группа симметрии судоку 2x5». Домашняя страница Фрейзера Джарвиса. Получено 11 сентября 2020.
- ^ Петтерсен (28 июля 2006 г.). "Re: Количество принципиально разных сеток судоку". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Матимагия (11 января 2020 г.). "Re: Количество возможных сеток судоку размером 16x16?". Форум новых игроков в судоку. Получено 14 сентября 2020.
- ^ «Математика Су-Доку: Общие - стр. 3». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ а б c d Петтерсен (10 января 2006 г.). «Математика Су-Доку: Общие - Страница 39». Форум новых игроков в судоку. Получено 8 ноября 2020. Ошибка цитирования: указанная ссылка ": 9" была определена несколько раз с разным содержанием (см. страница помощи).
- ^ «Математика Су-Доку - Re: оценка для 4x4 (стр. 37)». Форум новых игроков в судоку. 15 декабря 2005 г.. Получено 20 октября 2013.
- ^ PatmaxDaddy (12 января 2006 г.). "Алгоритм подсчета полос RxC Sudoku - Доказательство 4xC". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Петтерсен (9 января 2006 г.). "Алгоритм подсчета полос RxC Sudoku". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б PatmaxDaddy (11 февраля 2006 г.). "Re: RxC Sudoku алгоритм подсчета полос". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ а б c d Джарвис, Фрейзер (17 июня 2005 г.). «Перечисление возможных сеток судоку - Краткое изложение метода и результатов». Домашняя страница Фрейзера Джарвиса. Университет Шеффилда. Получено 20 октября 2013.
- ^ а б c d Красный Эд (13 декабря 2005 г.). «Математика Су-Доку - Re: оценка для 4x4 (стр. 37)». Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ "Алгоритм подсчета полос RxC Sudoku: Общие". Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ PatmaxDaddy (25 января 2006 г.). "Re: RxC Sudoku алгоритм подсчета полос". Форум новых игроков в судоку. Получено 20 октября 2013.
- ^ Петтерсен, Челл (31 октября 2006 г.). "Re: счет 6x2 [количество полос 6x2]". Форум новых игроков в судоку. Получено 5 октября 2020.
- ^ а б "Симметричная 17 загадок" Симметричная головоломка из 17 загадок.
- ^ а б "Рафаэль - 18 симметричных ключей" Рафаэль - 18 подсказок судоку с ортогональной симметрией.
- ^ а б «Полная симметрия» Полная симметрия - 24 разгадки судоку с полной симметрией.
- ^ а б «Турмалин - 19 ключей к двусторонней симметрии» Турмалин - ключ к разгадке судоку с двусторонней ортогональной симметрией.
- ^ "プ ロ グ ラ ミ ン グ パ ズ ル 談 コ ー ナ ー". .ic-net.or.jp. Получено 20 октября 2013.
- ^ «Минимальная судоку». Csse.uwa.edu.au. Получено 20 октября 2013.
- ^ Йирка, Боб (6 января 2012 г.). «Математики используют компьютер для решения задачи о минимальном решении судоку». PhysOrg. Получено 6 января 2012.
- ^ Макгуайр, Гэри (1 января 2012 г.). «Не существует судоку с 16 ключами: решение проблемы с минимальным количеством подсказок в судоку». arXiv:1201.0749. Цитировать журнал требует
| журнал =(помощь) - ^ Е. Х. Линь, I-C. Ву. «Нет 16-ти подсказок судоку от проекта sudoku @ vtaiwan» В архиве 14 февраля 2014 г. Wayback Machine, Сентябрь 2013.
- ^ "Симметрично-подсказанные 17". Forum.enjoysudoku.com. Получено 30 ноября 2013.
- ^ Таалман, Лаура (2007), «Серьезное отношение к судоку», Математические горизонты, 15 (1): 5–9, Дои:10.1080/10724117.2007.11974720, JSTOR 25678701, S2CID 126371771. См., В частности, рисунок 7, стр. 7.
- ^ «Низкие / высокие пороги подсказки». Forum.enjoysudoku.com. 14 августа 2019 г.. Получено 14 августа 2019.
- ^ http://forum.enjoysudoku.com Форум новых игроков в судоку.
- ^ а б [1] Минимальное количество подсказок для судоку
- ^ а б c d е http://forum.enjoysudoku.com Минимум данностей для больших головоломок.
- ^ と ん (январь 2015 г.). ヒ ン ト の 少 な い ナ ン プ レ 作 り 方 (на японском языке) (2-е изд.).暗 黒 通信 団. ISBN 978-4873102238. Архивировано из оригинал 11 августа 2014 г.
- ^ «Минимальное количество подсказок в Sudoku DG: варианты судоку». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «100 рандомизированных минимальных головоломок в стиле судоку с 6 ограничениями». Magictour.free.fr. Получено 20 октября 2013.
- ^ «Количество« волшебных судоку »(и случайная генерация): Общие - п. 2». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ "Судоку Сеттер". f-puzzles.com. Получено 11 августа 2020.
- ^ «Минимальная коллекция судоку-X». Sudocue.net. Получено 20 октября 2013.
- ^ «Скачать вложение» (PDF). Anthony.d.forbes.googlepages.com. Получено 20 октября 2013.
- ^ "Пазлы Ду-Сум-О". Bumblebeagle.org. Получено 20 октября 2013.
- ^ "Пазлы Ду-Сум-О". Bumblebeagle.org. Получено 20 октября 2013.
- ^ "Universiteit Leiden Opleiding Informatica: Внутренний отчет 2010-4: март 2010" (PDF). Liacs.nl. Получено 20 октября 2013.
- ^ [2][мертвая ссылка]
- ^ а б http://forum.enjoysudoku.com/high-clue-tamagotchis Тамагочи с высокой подсказкой (форум: страницы 1–14; минимальная подсказка 40: страница 10).
- ^ http://forum.enjoysudoku.com/high-clue-tamagotchis Важная подсказка тамагочи (форум: с. 5).
- ^ Бертье, Дени (4 декабря 2009 г.). «Беспристрастная статистика CSP - генератор контролируемого смещения». Получено 4 декабря 2009.
- ^ «Подсчет минимальных головоломок: подмножества, суперсеты и т. Д.». Forum.enjoysudoku.com. 11 июня 2013 г.. Получено 18 апреля 2017.
- ^ «Спросите несколько шаблонов, чтобы у них не было головоломок.: Общие». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «Самая большая« дыра »в судоку; самая большая« пустота »: Общие». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «Большое пустое пространство». Flickr. 6 мая 2008 г.. Получено 20 октября 2013.
- ^ «Наибольшее количество пустых групп?: Общие - п. 2». Forum.enjoysudoku.com. Получено 20 октября 2013.
- ^ «Ключи собраны в кластеры | Flickr - Photo Sharing!». Flickr. 25 марта 2008 г.. Получено 20 октября 2013.
- ^ "18 ключей к автоморфному судоку" 18 разгадываний автоморфных судоку.
- ^ «Шесть точек с пустым отверстием 5 × 5 | Flickr - Photo Sharing!». Flickr. 1 июля 2008 г.. Получено 20 октября 2013.
- ^ http://sudopedia.enjoysudoku.com/Canonical_Form «Каноническая форма».
дальнейшее чтение
- Розенхаус, Джейсон; Таалман, Лаура (2011). Серьезно относиться к судоку: математика, лежащая в основе самой популярной в мире головоломки с карандашом. Издательство Оксфордского университета.
внешняя ссылка
- Алгоритм карты различий В. Эльзера также решает судоку.
- Головоломка судоку - упражнение по ограниченному программированию и визуальному прологу 7 Карстен Келер Холст (in Визуальный пролог)
- Квадраты судоку и хроматические многочлены к Герцберг и Мурти рассматривает головоломки судоку как раскраска вершин проблемы в теория графов.