WikiDer > Подгруппа

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Подгруппа» – Новости · газеты · книги · ученый · JSTOR (Июнь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Алгебраическая структура → Теория групп Теория групп
Основные понятия Подгруппа Нормальная подгруппа Факторная группа (Полу-)прямой продукт Групповые гомоморфизмы ядро изображение прямая сумма венок просто конечный бесконечный непрерывный мультипликативный добавка циклический абелевский двугранный нильпотентный разрешимый Глоссарий теории групп Список тем теории групп
Конечные группы Классификация конечных простых групп циклический чередование Тип лжи спорадический Теорема Коши Теорема Лагранжа Теоремы Силова Теорема холла p-группа Элементарная абелева группа Группа Фробениуса Множитель Шура Симметричная группа Sп Кляйн четыре группы V Группа диэдра Dп Группа Quaternion Q Дициклическая группа Dicп
Дискретные группы Решетки Целые числа (Z) Бесплатная группа Модульные группы PSL (2,Z) SL (2,Z) Арифметическая группа Решетка Гиперболическая группа
Топологический и Группы Ли Соленоид Круг Общие линейные GL (п) Специальная линейная SL (п) Ортогональный O (п) Евклидово E (п) Специальные ортогональные ТАК(п) Унитарный U (п) Специальный унитарный SU (п) Симплектический Sp (п) грамм2 F4 E6 E7 E8 Лоренц Пуанкаре Конформный Диффеоморфизм Петля Бесконечномерная группа Ли O (∞) SU (∞) Sp (∞)
Алгебраические группы Линейная алгебраическая группа Редуктивная группа Абелева разновидность Эллиптическая кривая
v т е

В теория групп, филиал математика, учитывая группа грамм под бинарная операция ∗, а подмножество ЧАС из грамм называется подгруппа из грамм если ЧАС также образует группу относительно операции ∗. Точнее, ЧАС является подгруппой грамм если ограничение из ∗ в ЧАС × ЧАС это групповая операция над ЧАС. Обычно это обозначается ЧАС ≤ грамм, читать как "ЧАС является подгруппой грамм".

В тривиальная подгруппа любой группы есть подгруппа {е} состоящий только из элемента идентичности.

А собственная подгруппа группы грамм это подгруппа ЧАС который является правильное подмножество из грамм (то есть, ЧАС ≠ грамм). Обычно это обозначается как ЧАС < грамм, читать как "ЧАС собственная подгруппа в грамм". Некоторые авторы также исключают тривиальную группу из собственной (то есть ЧАС ≠ {е}).^[1][2]

Если ЧАС является подгруппой грамм, тогда грамм иногда называют сверхгруппа из ЧАС.

Те же определения применяются в более общем случае, когда грамм произвольный полугруппа, но в этой статье речь пойдет только о подгруппах групп. Группа грамм иногда обозначают упорядоченной парой (грамм, ∗), обычно, чтобы подчеркнуть операцию ∗, когда грамм несет несколько алгебраических или других структур.

Основные свойства подгрупп

• Подмножество ЧАС группы грамм является подгруппой грамм тогда и только тогда, когда он непустой и закрыто под произведениями и наоборот. (Условия закрытия означают следующее: всякий раз, когда а и б находятся в ЧАС, тогда ab и а⁻¹ также в ЧАС. Эти два условия можно объединить в одно эквивалентное условие: всякий раз, когда а и б находятся в ЧАС, тогда ab⁻¹ также в ЧАС.) В случае, если ЧАС конечно, то ЧАС это подгруппа если и только если ЧАС закрыт по продуктам. (В этом случае каждый элемент а из ЧАС порождает конечную циклическую подгруппу в ЧАС, и обратное а затем а⁻¹ = а^п−1, куда п это порядок а.)
• Вышеупомянутое условие можно сформулировать в виде гомоморфизм; то есть, ЧАС является подгруппой группы грамм если и только если ЧАС это подмножество грамм и имеется гомоморфизм включения (т. е. i (а) = а для каждого а) из ЧАС к грамм.
• В личность подгруппы - это тождество группы: если грамм это группа с идентичностью е_грамм, и ЧАС является подгруппой грамм с личностью е_ЧАС, тогда е_ЧАС = е_грамм.
• В обратный элемента в подгруппе является обратным элементу в группе: если ЧАС является подгруппой группы грамм, и а и б являются элементами ЧАС такой, что ab = ба = е_ЧАС, тогда ab = ба = е_грамм.
• В пересечение подгрупп А и B снова подгруппа.^[3] В союз подгрупп А и B является подгруппой тогда и только тогда, когда либо А или же B содержит другой, так как, например, 2 и 3 являются объединением 2Z и 3Z, а их сумма 5 - нет. Другой пример - объединение оси x и оси y на плоскости (с операцией сложения); каждый из этих объектов является подгруппой, а их объединение - нет. Это также служит примером двух подгрупп, пересечение которых в точности совпадает.
• Если S это подмножество грамм, то существует минимальная подгруппа, содержащая S, который можно найти, взяв пересечение всех подгрупп, содержащих S; он обозначается ⟨S⟩ И считается подгруппа, порожденная S. Элемент грамм в ⟨S⟩ Тогда и только тогда, когда это конечное произведение элементов S и их обратные.
• Каждый элемент а группы грамм порождает циклическую подгруппу ⟨а⟩. Если ⟨а⟩ является изоморфный к Z/пZ для некоторого положительного целого числа п, тогда п это наименьшее положительное целое число, для которого а^п = е, и п называется порядок из а. Если ⟨а⟩ Изоморфен Z, тогда а говорят, что имеет бесконечный порядок.
• Подгруппы любой данной группы образуют полная решетка при включении, называется решетка подгрупп. (В то время как инфимум вот обычное теоретико-множественное пересечение, супремум множества подгрупп является подгруппой создано теоретико-множественное объединение подгрупп, а не само теоретико-множественное объединение.) Если е это личность грамм, то тривиальная группа {е} это минимум подгруппа грамм, в то время как максимум подгруппа - это группа грамм сам.

G - группа ${displaystyle mathbb {Z} / 8mathbb {Z}}$, то целые числа по модулю 8 под дополнением. Подгруппа H содержит только 0 и 4 и изоморфна ${displaystyle mathbb {Z} / 2mathbb {Z}}$. У H есть четыре левых смежных класса: сам H, 1 + H, 2 + H и 3 + H (написано с использованием аддитивной записи, поскольку это аддитивная группа). Вместе они разбивают всю группу G на непересекающиеся множества равного размера. Индекс [G: H] равен 4.

Козеты и теорема Лагранжа

Учитывая подгруппу ЧАС и немного а в G определим оставили смежный ах = {ах : час в ЧАС}. Потому что а обратимо, отображение φ: ЧАС → ах задается формулой φ (час) = ах это биекция. Кроме того, каждый элемент грамм содержится ровно в одном левом классе ЧАС; левые смежные классы - классы эквивалентности, соответствующие отношение эквивалентности а₁ ~ а₂ если и только если а₁⁻¹а₂ в ЧАС. Количество левых смежных классов ЧАС называется индекс из ЧАС в грамм и обозначается [грамм : ЧАС].

Теорема Лагранжа утверждает, что для конечной группы грамм и подгруппа ЧАС,

${displaystyle [G: H] = {| G | над | H |}}$

где |грамм| и |ЧАС| обозначить заказы из грамм и ЧАС, соответственно. В частности, порядок каждой подгруппы грамм (и порядок каждого элемента грамм) должен быть делитель из |грамм|.^[4][5]

Правые классы аналогично определяются: Ха = {ха : час в ЧАС}. Они также являются классами эквивалентности для подходящего отношения эквивалентности, и их количество равно [грамм : ЧАС].

Если ах = Ха для каждого а в грамм, тогда ЧАС считается нормальная подгруппа. Каждая подгруппа индекса 2 является нормальной: левые смежные классы, а также правые смежные классы - это просто подгруппа и ее дополнение. В более общем смысле, если п наименьшее простое число, делящее порядок конечной группы ГРАММ, то любая подгруппа индекса п (если таковой существует) нормально.

Пример: подгруппы Z₈

Позволять грамм быть циклическая группа Z₈ чьи элементы

${displaystyle G = left {0,2,4,6,1,3,5,7ight}}$

и чья групповая операция сложение по модулю восемь. Его Стол Кэли является

В этой группе есть две нетривиальные подгруппы: J={0,4} и ЧАС={0,2,4,6}, куда J также является подгруппой ЧАС. Стол Кэли для ЧАС верхний левый квадрант таблицы Кэли для грамм. Группа грамм является циклический, и его подгруппы. В общем случае подгруппы циклических групп также являются циклическими.

Пример: подгруппы S₄ (в симметричная группа на 4 элемента)

Каждая группа имеет столько же малых подгрупп, сколько нейтральных элементов на главной диагонали:

В тривиальная группа и двухэлементные группы Z₂. Эти небольшие подгруппы не включены в следующий список.

В симметричная группа S4 показывая все перестановки из 4 элементов

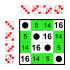
Все 30 подгрупп Упрощенный Диаграммы Хассе из решетка подгрупп из S4

12 элементов

В переменная группа А₄ показывая только даже перестановки

Подгруппы:

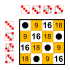
8 элементов

Группа диэдра порядка 8 Подгруппы:

Диэдральная группа порядка 8 Подгруппы:

Диэдральная группа порядка 8 Подгруппы:

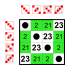
6 элементов

Симметричная группа S3 Подгруппа:

Симметричная группа S3 Подгруппа:

Симметричная группа S3 Подгруппа:

Симметричная группа S3 Подгруппа:

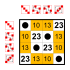
4 элемента

Кляйн четыре группы

Кляйн четыре группы

Кляйн четыре группы

Кляйн четыре группы

Циклическая группа Z4

Циклическая группа Z4

Циклическая группа Z4

3 элемента

Циклическая группа Z3

Циклическая группа Z3

Циклическая группа Z3

Циклическая группа Z3

Другие примеры

• Четные целые числа являются подгруппой аддитивной группы целых чисел: когда вы складываете два четных числа, вы получаете четное число.
• An идеальный в кольце ${displaystyle R}$ является подгруппой аддитивной группы ${displaystyle R}$.
• А линейное подпространство из векторное пространство является подгруппой аддитивной группы векторов.
• Позволять ${displaystyle A}$ быть абелева группа; элементы ${displaystyle A}$ которые имеют конечный период образуют подгруппу ${displaystyle A}$ называется торсионная подгруппа из ${displaystyle A}$.

Смотрите также

• Подгруппа Картана
• Подгруппа фитингов
• Стабильная подгруппа
• Подгруппа фиксированной точки
• Подгруппа теста

Примечания

Рекомендации

• Джейкобсон, Натан (2009), Базовая алгебра, 1 (2-е изд.), Дувр, ISBN 978-0-486-47189-1.
• Хангерфорд, Томас (1974), Алгебра (1-е изд.), Springer-Verlag, ISBN 9780387905181.
• Артин, Майкл (2011), Алгебра (2-е изд.), Прентис Холл, ISBN 9780132413770.
• С., Даммит, Дэвид (2004). Абстрактная алгебра. Фут, Ричард М., 1950- (3-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN 9780471452348. OCLC 248917264.