WikiDer > Дициклическая группа

Алгебраическая структура → Теория групп Теория групп
Основные понятия Подгруппа Нормальная подгруппа Факторная группа (Полу-)прямой продукт Групповые гомоморфизмы ядро образ прямая сумма венок просто конечный бесконечный непрерывный мультипликативный добавка циклический абелевский двугранный нильпотентный разрешимый Глоссарий теории групп Список тем теории групп
Конечные группы Классификация конечных простых групп циклический чередование Тип лжи спорадический Теорема Коши Теорема Лагранжа Теоремы Силова Теорема холла p-группа Элементарная абелева группа Группа Фробениуса Множитель Шура Симметричная группа Sп Кляйн четыре группы V Группа диэдра Dп Группа Quaternion Q Дициклическая группа Dicп
Дискретные группы Решетки Целые числа (Z) Бесплатная группа Модульные группы PSL (2,Z) SL (2,Z) Арифметическая группа Решетка Гиперболическая группа
Топологический и Группы Ли Соленоид Круг Общие линейные GL (п) Специальная линейная SL (п) Ортогональный O (п) Евклидово E (п) Специальные ортогональные ТАК(п) Унитарный U (п) Специальный унитарный SU (п) Симплектический Sp (п) г2 F4 E6 E7 E8 Лоренц Пуанкаре Конформный Диффеоморфизм Петля Бесконечномерная группа Ли O (∞) SU (∞) Sp (∞)
Алгебраические группы Линейная алгебраическая группа Редуктивная группа Абелева разновидность Эллиптическая кривая
v т е

эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью от добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Дициклическая группа» – Новости · газеты · книги · ученый · JSTOR (Февраль 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В теория групп, а дициклическая группа (обозначение Dic_п или Q_4п,^[1] ⟨п, 2,2⟩) - особый вид неабелева группа из порядок 4п (п > 1). Это расширение из циклическая группа порядка 2 циклической группой порядка 2п, давая имя дициклический. В обозначениях точные последовательности групп, это расширение можно выразить как:

${ displaystyle 1 to C_ {2n} to { mbox {Dic}} _ {n} to C_ {2} to 1. ,}$

В более общем плане, учитывая любые конечный абелеву группу с элементом порядка 2, можно определить дициклическую группу.

Определение

Для каждого целое число п > 1 дициклическая группа Dic_п можно определить как подгруппа подразделения кватернионы Сгенерированно с помощью

${ displaystyle { begin {align} a & = e ^ {i pi / n} = cos { frac { pi} {n}} + i sin { frac { pi} {n}} x & = j end {выровнено}}}$

Более абстрактно можно определить дициклическую группу Dic_п как группа со следующими презентация^[2]

${ displaystyle operatorname {Dic} _ {n} = langle a, x mid a ^ {2n} = 1, x ^ {2} = a ^ {n}, x ^ {- 1} ax = а ^ {- 1} rangle. , !}$

Некоторые вещи, которые следует отметить, вытекают из этого определения:

• Икс⁴ = 1
• Икс²а^k = а^k+п = а^kИкс²
• если j = ± 1, то Икс^jа^k = а^−kИкс^j.
• а^kИкс⁻¹ = а^k−па^пИкс⁻¹ = а^k−пИкс²Икс⁻¹ = а^k−пИкс.

Таким образом, каждый элемент Dic_п можно однозначно записать как а^kИкс^j, где 0 ≤ k < 2п и j = 0 или 1. Правила умножения задаются формулой

• ${ displaystyle a ^ {k} a ^ {m} = a ^ {k + m}}$
• ${ displaystyle a ^ {k} a ^ {m} x = a ^ {k + m} x}$
• ${ displaystyle a ^ {k} xa ^ {m} = a ^ {k-m} x}$
• ${ displaystyle a ^ {k} xa ^ {m} x = a ^ {k-m + n}}$

Отсюда следует, что Dic_п имеет порядок 4п.^[2]

Когда п = 2, дициклическая группа изоморфный к группа кватернионов Q. В более общем плане, когда п является степенью двойки, дициклическая группа изоморфна группе обобщенная группа кватернионов.^[2]

Свойства

Для каждого п > 1 дициклическая группа Dic_п это неабелева группа порядка 4п. (Для вырожденного случая п = 1 группа Dic₁ циклическая группа C₄, который не считается дициклическим.)

Позволять А = ⟨а⟩ - подгруппа в Dic_п генерируется от а. потом А циклическая группа порядка 2п, так что [Dic_п:А] = 2. Как подгруппа показатель 2 это автоматически нормальная подгруппа. Фактор-группа Dic_п/А - циклическая группа порядка 2.

Dic_п является разрешимый; Обратите внимание, что А является нормальным и, будучи абелевым, само разрешимо.

Бинарная группа диэдра

Дициклическая группа - это бинарная группа полиэдров - это один из классов подгрупп группы Группа контактов Штырь₋(2), которая является подгруппой группы Спиновая группа Спин (3) - и в этом контексте известен как бинарная группа диэдра.

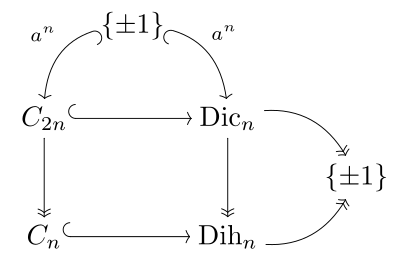
Связь с бинарная циклическая группа C_2п, циклическая группа C_п, а группа диэдра Dih_п порядка 2п показан на диаграмме справа и параллелен соответствующей диаграмме для группы контактов. Кокстер пишет бинарная группа диэдра как ⟨2,2,п⟩ и бинарная циклическая группа с уголками, ⟨п⟩.

Существует внешнее сходство между дициклическими группами и диэдральные группы; оба являются своего рода «зеркальным отражением» лежащей в основе циклической группы. Но представление диэдральной группы имело бы Икс² = 1 вместо Икс² = а^п; и это дает другую структуру. В частности, Dic_п это не полупрямой продукт из А и ⟨Икс⟩, поскольку А ∩ ⟨Икс⟩ Нетривиально.

Дициклическая группа обладает уникальным инволюция (т.е. элемент порядка 2), а именно Икс² = а^п. Обратите внимание, что этот элемент находится в центр Дик_п. Действительно, центр состоит исключительно из элемента идентичности и Икс². Если мы добавим соотношение Икс² = 1 к представлению Dic_п можно получить представление группа диэдра Dih_2п, поэтому фактор-группа Dic_п/<Икс²> изоморфен Dih_п.

Есть естественное соотношение 2 к 1 гомоморфизм от группы единичных кватернионов к 3-мерному группа ротации описанный в кватернионы и пространственные вращения. Поскольку дициклическая группа может быть вложена внутрь единичных кватернионов, можно спросить, каков ее образ при этом гомоморфизме. Ответ просто диэдральная группа симметрии Dih_п. По этой причине дициклическая группа также известна как бинарная группа диэдра. Обратите внимание, что дициклическая группа не содержит подгруппы, изоморфной Dih_п.

Аналогичное построение прообраза с помощью Pin₊(2) вместо булавки₋(2) дает еще одну группу диэдра Dih_2п, а не дициклическая группа.

Обобщения

Позволять А быть абелева группа, имеющий определенный элемент у в А с заказом 2. Группа г называется обобщенная дициклическая группа, записанный как Дик (А, у), если он генерируется А и дополнительный элемент Икс, и вдобавок у нас есть [г:А] = 2, Икс² = у, и для всех а в А, Икс⁻¹топор = а⁻¹.

Поскольку для циклической группы четного порядка всегда существует единственный элемент порядка 2, мы можем видеть, что дициклические группы - это просто особый тип обобщенной дициклической группы.

Смотрите также

• бинарная группа полиэдров
• бинарная циклическая группа, ⟨п⟩, Порядок 2п
• бинарная тетраэдрическая группа, 2T = ⟨2,3,3⟩, порядок 24
• бинарная октаэдрическая группа, 2O = ⟨2,3,4⟩, порядок 48
• бинарная группа икосаэдра, 2I = ⟨2,3,5⟩, порядок 120

использованная литература

внешние ссылки

• Дициклические группы на GroupNames