WikiDer > Точка Мисюревича - Википедия
В математике Точка Мисюревича параметр в Набор Мандельброта (в пространство параметров квадратичных многочленов), для которых критическая точка является строго предпериодическим (т.е. становится периодическим после конечного числа итераций, но сам не является периодическим). По аналогии термин Точка Мисюревича также используется для параметров в мультиброт набор где единственная критическая точка строго предпериодическая. (Этот термин имеет меньший смысл для карт в более широком смысле, которые имеют более одной (свободной) критической точки, потому что некоторые критические точки могут быть периодическими, а другие нет.)
Математические обозначения
Параметр точка Мисюревича если он удовлетворяет уравнениям
и
так :
куда :
- это критическая точка из ,
- и положительные целые числа,
- обозначает -я итерация .
Имя
Очки Мисюревича названы в честь польско-американского математик Михал Мисюревич.[1]
Обратите внимание, что термин «точка Мисюревича» используется неоднозначно: Мисюревич первоначально исследовал карты, в которых все критические точки не повторялись (то есть, есть окрестность каждой критической точки, которую не посещает орбита этой критической точки), и этот смысл твердо установлен в контексте динамики повторяющихся интервальных отображений.[2] Случай, когда для квадратичного многочлена единственная критическая точка является строго предпериодической, является лишь очень частным случаем; в этом ограниченном смысле (как описано выше) этот термин используется в сложной динамике; более подходящий термин был бы Очки Мисюревича – Терстона (после Уильям Терстон, исследовавший посткритически конечные рациональные отображения).
Синонимы
- хаб (в случае точки ветвления)
Квадратичные карты
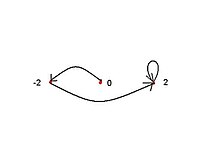
А комплексный квадратичный многочлен имеет только одну критическую точку. Подходящим спряжение любой квадратичный многочлен можно преобразовать в отображение вида который имеет единственную критическую точку в . Точки Мисюревича этого семейства карт равны корни уравнений
- ,
(при условии непериодичности критической точки), где:
Например, Мисюревич указывает на k= 2 и п= 1, обозначаемый M2,1, корни
- .
Корень c= 0 не является точкой Мисюревича, поскольку критическая точка фиксированная точка когда c= 0, и поэтому является периодическим, а не предпериодическим. Остается одна точка Мисюревича. M2,1 в c = −2.
Свойства точек Мисиуревича комплексного квадратичного отображения
Очки Мисюревича принадлежат граница из Набор Мандельброта. Очки Мисюревича плотный в граница из Набор Мандельброта.[3][4]
Если является точкой Мисюревича, то ассоциированная заполненный Юля набор равно Юля набор, а значит заполненный Юля набор не имеет интерьер.
Если является точкой Мисюревича, то в соответствующем множестве Жюлиа все периодические циклы отталкиваются (в частности, цикл, на который падает критическая орбита).
В Набор Мандельброта и Юля набор локально асимптотически самоподобный вокруг точек Мисюревича.[5]
Типы
Точки Мисюревича можно классифицировать по количеству падающих на них внешних лучей:,[3] точки, где встречаются ветви
- точки ветвления (= точки, которые разделяют набор Мандельброта минимум на три компонента.) с 3 или более внешние аргументы (углы)
- точки без ветвления с ровно двумя внешними аргументами (= внутренние точки дуг в множестве Мандельброта): эти точки менее заметны и, следовательно, их не так легко найти на изображениях.
- конечные точки с 1 внешним аргументом (кончики веток)
Согласно теореме о ветвлении множества Мандельброта,[4] все точки ветвления множества Мандельброта являются точками Мисюревича (плюс, в комбинаторном смысле, гиперболические компоненты, представленные их центрами).[3][4]
Многие (на самом деле большинство) параметров Мисюревича в множестве Мандельброта выглядят как "центры спиралей".[6] Объяснение этому следующее: при параметре Мисиуревича критическое значение перескакивает на отталкивающий периодический цикл после конечного числа итераций; в каждой точке цикла множество Жюлиа асимптотически самоподобно путем комплексного умножения на производную этого цикла. Если производная не является действительной, то это означает, что множество Жюлиа около периодического цикла имеет спиральную структуру. Таким образом, аналогичная спиральная структура имеет место в множестве Жюлиа вблизи критического значения и, согласно Тан Лейвышеупомянутой теоремы, также в множестве Мандельброта около любого параметра Мисюревича, для которого отталкивающая орбита имеет ненастоящий множитель. В зависимости от значения множителя спиральная форма может казаться более или менее выраженной. Количество ветвей спирали равно количеству ветвей по параметру Мисюревича, и это равно количеству ветвей при критическом значении в множестве Жюлиа. (Даже `` главная точка Мисиуревича в 1/3 лимба '' на конце параметрических лучей под углами 9/56, 11/56 и 15/56 оказывается асимптотически спиралью с бесконечным числом витков , хотя без увеличения это трудно увидеть.)
Внешние аргументы
Внешние аргументы точек Мисюревича, измеренных в повороты находятся :
- рациональное число
- правильная дробь с четное знаменатель
- диадические дроби со знаменателем и конечный ( прекращение ) расширение, например:
- дробь со знаменателем и повторяющееся расширение подобно :
- .[7]
где: a и b - положительные целые числа, а b - нечетные, номер нижнего индекса показывает основание система счисления.
Примеры точек Мисюревича комплексного квадратичного отображения
Конечные точки
Точка :
- это кончик нити[8]
- Его критические орбиты [9]
- точка приземления внешний луч для угла = 1/6
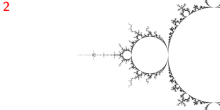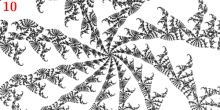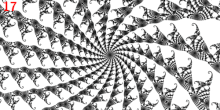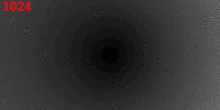
Точка
- конечная точка основной антенны Набор Мандельброта [10]
- Его критические орбиты [9]
- Символическая последовательность = C L R R R ...
- препериод 2 и период 1
Обратите внимание, что это z-плоскость (динамический самолет) не c-плоскость (плоскость параметров) и точка это не то же самое, что .
Точка это точка приземления только одного внешний луч (луч параметра) угла 1/2.
Точки не ветвления
Точка находится недалеко от мыса Мисюревич . это
- центр двухрукавной спирали
- точка посадки 2х внешних лучей с углами: и где знаменатель
- предпериодическая точка с предпериодом и период
Точка находится недалеко от мыса Мисюревич ,
- которая является точкой посадки пары лучей: ,
- имеет предпериод и период
Пункты отделения
Точка
- главная точка Мисюревича 1/3 конечности
- он имеет 3 внешние лучи: 9/56, 11/56 и 15/56.
Смотрите также
Рекомендации
- ^ Домашняя страница Михала Мисюревича, Университет Индианы - Университет Пердью Индианаполис
- ^ Веллингтон де Мело, Себастьян ван Стриен, «Одномерная динамика». Монография, Springer Verlag (1991)
- ^ а б c Адриан Дуади, Джон Хаббард, "Динамический этюд комплексов полиномов", предварительные публикации mathématiques d'Orsay, 1982/1984
- ^ а б c Дирк Шлейхер, "О волокнах и локальной связности множеств Мандельброта и мультиброта", в: М. Лапидус, М. ван Франкенхейзен (редакторы): Фрактальная геометрия и приложения: юбилей Бенуа Мандельброта. Proceedings of Symposia in Pure Mathematics 72, American Mathematical Society (2004), 477–507 или онлайн-статья с arXiv.org
- ^ Lei.pdf Тан Лей, «Сходство между множеством Мандельброта и множеством Жюлиа», Сообщения по математической физике 134 (1990), стр. 587-617.
- ^ Граница множества Мандельброта В архиве 2003-03-28 на Wayback Machine Авторы: Майкл Фрейм, Бенуа Мандельброт и Ниал Негер
- ^ Двоичные десятичные числа и десятичные числа, отличные от десятичной, Томас Ким-вай Ён и Эрик Кин-Кеунг Пун
- ^ Наконечник нитей Роберта П. Мунафо
- ^ а б Препериодические (Мисюревич) точки в теории Мандельброта Евгений Демидов
- ^ кончик главных антенн Роберта П. Мунафо
- Михал Мисюревич (1981), «Абсолютно непрерывные меры для определенных карт интервала». Publications Mathématiques de l'IHÉS, 53 (1981), стр. 17-51
внешняя ссылка
| В Викиучебнике есть книга на следующие темы: Фракталы |
| Викискладе есть медиафайлы по теме Категория: мыс Мисюревич. |