WikiDer > Монохроматическая плоская электромагнитная волна

В общая теория относительности, то монохроматическая электромагнитная плоская волна в пространстве-времени является аналогом монохроматических плоских волн, известных из теории Максвелла. Точное определение решения довольно сложно, но очень поучительно.

Любой точное решение из Уравнение поля Эйнштейна который моделирует электромагнитное поле, должны учитывать все гравитационные эффекты энергия и масса из электромагнитное поле. Помимо электромагнитного поля, если нет материи и присутствуют негравитационные поля, мы должны одновременно решить уравнение поля Эйнштейна и Полевые уравнения Максвелла.

В Теория Максвелла из электромагнетизм, одним из наиболее важных типов электромагнитного поля являются те, которые представляют электромагнитное излучение. Из них наиболее важными примерами являются электромагнитные плоские волны, в котором излучение имеет плоские волновые фронты, движущиеся в определенном направлении со скоростью света. Из них самыми основными являются монохромный плоские волны, в которых только одна частота компонент присутствует. Это именно то явление, которое наше решение будет моделировать в терминах общей теории относительности.

Определение решения

Метрический тензор единственного точного решения, моделирующего линейно поляризованный электромагнитная плоская волна с амплитуда q и частота ω можно записать в терминах Координаты Розена, в виде

${ displaystyle ds ^ {2} = - 2 , du , dv + C ^ {2} left ({ frac {q ^ {2}} { omega ^ {2}}}, 2 { frac {q ^ {2}} { omega ^ {2}}}, omega u right) , left (dx ^ {2} + dy ^ {2} right), qquad - infty$

где ${ displaystyle xi = { frac {u_ {0}} { omega}}}$ является первым положительным корнем из C(а, 2а, ξ) = 0 где ${ displaystyle a = { frac {q ^ {2}} { omega ^ {2}}}}$. На этой диаграмме ∂_ты, ∂_v находятся значение NULL векторов координат в то время как ∂_Икс, ∂_у находятся космический координатные векторы.

Здесь Матьё косинус C(а, б, ξ) является даже функция который решает Уравнение Матье а также принимает значение C(а, б, 0) = 1. Несмотря на название, эта функция нет периодический, и его нельзя записать в терминах синусоидальных или даже гипергеометрических функций. (Видеть Функция Матье для получения дополнительной информации о функции косинуса Матьё.)

В нашем выражении для метрики заметим, что ∂_ты, ∂_v находятся нулевой вектор поля. Следовательно, ∂_ты + ∂_v это времяподобный вектор поле, а ∂_ты − ∂_v, ∂_Икс, ∂_у находятся космический вектор поля.

Чтобы определить электромагнитное поле, мы можем взять электромагнитное четырехвекторный потенциал

${ displaystyle { vec {A}} = { frac {{ sqrt {2}} a int C left ({ frac {u ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right) , sin ( omega u) , du} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right)}} ; partial _ {x }}$

Теперь у нас есть полное описание математической модели, сформулированной в общей теории относительности.

Локальные изометрии

Наше пространство-время моделируется Лоренцево многообразие который обладает замечательной симметрией. А именно, наше пространство-время допускает шестимерную группу Ли самоизометрий. Эта группа порождается шестимерным Алгебра Ли из Убивающие векторные поля. Удобный базис состоит из одного нулевого векторного поля,

${ displaystyle { vec { xi}} _ {1} = partial _ {v}}$

три пространственноподобных векторных поля,

${ Displaystyle { vec { xi}} _ {2} = partial _ {x}, ; { vec { xi}} _ {3} = partial _ {y}, ; { vec { xi}} _ {4} = - y , partial _ {x} + x , partial _ {y}}$

и два дополнительных векторных поля,

${ displaystyle { begin {align} { vec { xi}} _ {5} & = x , partial _ {v} + int { frac {du} {C left ({ frac { q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right)}} , partial _ {x} { vec { xi}} _ {6} & = y , partial _ {v} + int { frac {du} {C left ({ frac {q ^ {2 }} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right)}} , partial _ {y} конец {выровнен}}}$

Вот, ${ displaystyle { vec { xi}} _ {2}, , { vec { xi}} _ {3}, , { vec { xi}} _ {4}}$ генерировать Евклидова группа, действующей внутри каждого плоского волнового фронта, что оправдывает название плоская волна для этого решения. Также ${ displaystyle { vec { xi}} _ {5}, , { vec { xi}} _ {6}}$ показать, что все непереверсивные направления эквивалентны. Это соответствует хорошо известному факту, что в плоском пространстве-времени две сталкивающиеся плоские волны всегда сталкиваются. недвусмысленно когда представлены в соответствующем Рама Лоренца.

На будущее отметим, что эта шестимерная группа самоизометрий действует переходно, так что наше пространство-время однородный. Однако это не изотропный, поскольку поперечные направления отличаются от непоперечных.

Семья инерциальных наблюдателей

В поле кадра

${ displaystyle { vec {e}} _ {0} = { frac {1} { sqrt {2}}} left ( partial _ {u} + partial _ {v} right)}$

${ displaystyle { vec {e}} _ {1} = { frac {1} { sqrt {2}}} left (- partial _ {u} + partial _ {v} right)}$

${ displaystyle { vec {e}} _ {2} = { frac {1} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, , { гидроразрыв {2q ^ {2}} { omega ^ {2}}}, , omega u right)}} partial _ {x}}$

${ displaystyle { vec {e}} _ {3} = { frac {1} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, , { гидроразрыв {2q ^ {2}} { omega ^ {2}}}, , omega u right)}} partial _ {y}}$

представляет местная рамка Лоренца определяется семьей неподвижные инерциальные наблюдатели. Это,

${ displaystyle nabla _ {{ vec {e}} _ {0}} { vec {e}} _ {0} = 0}$

что означает, что интегральные кривые из подобный времени единичное векторное поле е₀ подобны времени геодезические, а также

${ displaystyle nabla _ {{ vec {e}} _ {0}} { vec {e}} _ {1} = nabla _ {{ vec {e}} _ {0}} { vec {e}} _ {2} = nabla _ {{ vec {e}} _ {0}} { vec {e}} _ {3} = 0}$

что означает, что космический Единичные векторные поля е₁, е₂, е₃ не вращаются. (Они есть Ферми – Уокер перевезен.) Здесь, ${ displaystyle { vec {e}} _ {0}}$ является времениподобным единичным векторным полем, а ${ displaystyle { vec {e}} _ {1}, { vec {e}} _ {2}, { vec {e}} _ {3}}$ пространственноподобные единичные векторные поля.

Невращающиеся инерциальные системы отсчета настолько близки, насколько мы можем, в искривленном пространстве-времени к обычному Рамы Лоренца известно из специальная теория относительности, где Преобразования Лоренца являются просто переходами от одной системы координат Лоренца к другой.

Электромагнитное поле

Что касается нашей системы отсчета, электромагнитное поле, полученное из потенциала, указанного выше, равно

${ displaystyle { vec {E}} = q , sin ( omega u) , { vec {e}} _ {2}}$

${ displaystyle { vec {B}} = - q , sin ( omega u) , { vec {e}} _ {3}}$

Это электромагнитное поле - без источника решение уравнений поля Максвелла на конкретном искривленном пространстве-времени, которое определяется указанным выше метрическим тензором. Это нулевое решение, и он представляет собой поперечный синусоидальная электромагнитная плоская волна с амплитудой q и частота ω, путешествуя по е₁ направление. Когда мы

• вычислить тензор энергии-импульса Т^ab для данного электромагнитного поля,
• вычислить Тензор Эйнштейна г^ab для данного метрического тензора

мы находим, что уравнение поля Эйнштейна г^ab = 8πT^ab доволен. Вот что мы имеем в виду, говоря, что у нас есть точный электровакуумный раствор.

В рамках нашей системы тензор энергии-импульса оказывается

${ displaystyle T ^ {{ hat {j}} { hat {k}}} = { frac {q ^ {2} sin ^ {2} ( omega u)} {4 pi}} { begin {bmatrix} 1 & 1 & 0 & 0 1 & 1 & 0 & 0 0 & 0 & 0 & 0 0 & 0 & 0 & 0 end {bmatrix}}}$

Это точно такое же выражение что мы найдем в классическом электромагнетизме (где мы пренебрегаем гравитационными эффектами энергии электромагнитного поля) для нулевого поля, указанного выше; единственная разница в том, что теперь наша рамка анголономный (ортонормированный) базис на искривленное пространство-время, а не координатная база в плоское пространство-время. (Видеть поля кадра.)

Относительное движение наблюдателей

Диаграмма Розена называется сопутствующий с нашей семьей инерциальных невращающихся наблюдателей, потому что координаты v − ты, Икс, у все постоянны вдоль каждой мировой линии, заданной интегральной кривой времениподобного единичного векторного поля ${ displaystyle { vec {X}} = { vec {e}} _ {0}}$. Таким образом, на карте Розена эти наблюдатели могут казаться неподвижными. Но на самом деле они движутся относительно друг друга. Чтобы убедиться в этом, мы должны вычислить их тензор разложения относительно кадра, приведенного выше. Это оказывается

${ displaystyle theta [{ vec {X}}] _ {{ hat {i}} { hat {j}}} = { frac { omega} { sqrt {2}}} , { frac {C ^ { prime} ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}) , omega u)} {C ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u)}} , operatorname {diag} (0,1,1)}$

где

${ displaystyle C ^ { prime} (a, q, xi) = { frac { partial C (a, q, xi)} { partial xi}}.}$

Ненулевые компоненты идентичны и являются

1. вогнуться ${ Displaystyle -u_ {0} <и <и_ {0}}$
2. исчезнуть в ты = 0.

Физически это означает, что небольшое сферическое «облако» наших инерциальных наблюдателей парит на мгновение в ты = 0 а потом начинают рушиться, в конце концов проходя друг через друга в ты = ты₀. Если представить их как образующие трехмерное облако из однородно распределенных пробных частиц, этот коллапс происходит перпендикулярно направлению распространения волны. Облако не демонстрирует относительного движения в направлении распространения, так что это чисто поперечный движение.

За ${ displaystyle { frac {q} { omega}} ll 1}$ (коротковолновое приближение) примерно

${ Displaystyle г_ {хх} приблизительно соз (кв) ^ {2}}$

${ displaystyle theta [{ vec {X}}] _ {22} приблизительно -q , tan (qu)}$ Например, с ${ Displaystyle д = 1/2, омега = 5}$, у нас есть

где точные выражения показаны красным цветом, а коротковолновые приближения - зеленым.

В тензор завихренности нашего совпадения исчезает одинаково, поэтому мировые линии наших наблюдателей гиперповерхность ортогональная. Трехмерный Тензор Римана гиперпространств задается относительно нашего каркаса соотношением

${ displaystyle {{} ^ {3} R} _ {1212} = {{} ^ {3} R} _ {1313} = q ^ {2} , sin ( omega u) ^ {2}}$

${ displaystyle {{} ^ {3} R} _ {2323} = { frac {- omega ^ {2}} {2}} , { frac {C ^ { prime} left ({ гидроразрыв {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right) ^ {2}} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u справа) ^ {2}}}}$

Кривизна четко разделяется на волну (кривизна в разрезе, параллельная направлению распространения) и фон (кривизна в разрезе).

Тензор кривизны Римана

Напротив, Bel разложение тензора кривизны Римана, взятого относительно ${ displaystyle { vec {X}} = { vec {e}} _ {0}}$, это сама простота. В электрогравитационный тензор, который непосредственно представляет приливные ускорения, является

${ displaystyle E [{ vec {X}}] _ {{ hat {m}} { hat {n}}} = q ^ {2} , sin ( omega u) ^ {2} , operatorname {diag} (0,1,1)}$

В магнитогравитационный тензор, который непосредственно представляет спин-спиновая сила на гироскопе, который несет один из наших наблюдателей,

${ displaystyle B [{ vec {X}}] _ {{ hat {m}} { hat {n}}} = q ^ {2} , sin ( omega u) ^ {2} { begin {bmatrix} 0 & 0 & 0 0 & 0 & -1 0 & 1 & 0 end {bmatrix}}}$

(The топогравитационный тензор, который представляет собой пространственные изгибы сечения, согласуется с тензором электрогравитации.)

Оглядываясь на наш график метрического тензора, мы видим, что приливный тензор производит небольшие синусоидальные относительные ускорения с периодом ω, которые являются чисто поперечными к направлению распространения волны. Чистый гравитационный эффект на протяжении многих периодов состоит в том, чтобы произвести цикл расширения и повторного сжатия нашей семьи инерционных не вращающихся наблюдателей. Это можно рассматривать как эффект кривизна фона произведенный волной.

Этот цикл расширения и повторного схлопывания напоминает расширение и повторное сжатие. Космологические модели FRW, и это происходит по той же причине: наличие негравитационной массы-энергии. В моделях FRW эта масса-энергия обусловлена ​​массой пылевых частиц; здесь это связано с полевой энергией электромагнитного поля. Здесь цикл расширения-повторного схлопывания начинается и заканчивается сильный скаляр кривизна особенность; здесь у нас просто координатная особенность (обстоятельство, которое сильно смутило Эйнштейна и Розена в 1937 году). Кроме того, здесь имеется небольшая синусоидальная модуляция расширения и повторного сжатия.

Оптические эффекты

Общий принцип состояний плоских волн вы не видите, как волновой поезд входит на станцию, но вы можете видеть, как он уходит. То есть, если вы посмотрите через встречные волновые фронты на удаленные объекты, вы не увидите оптических искажений, но если вы повернетесь и посмотрите через уходящие волновые фронты на удаленный объект, вы буду увидеть оптические искажения. В частности, нулевая геодезическая конгруэнтность генерируется нулевым векторным полем ${ displaystyle { vec {k}} = { vec {e}} _ {0} + { vec {e}} _ {1}}$ исчезает оптические скаляры, но нулевая геодезическая конгруэнция, порожденная ${ displaystyle { vec { ell}} = { vec {e}} _ {0} - { vec {e}} _ {1}}$ имеет исчезающие скаляры скручивания и сдвига, но ненулевой скаляр расширения

${ displaystyle theta = { sqrt {2}} omega , { frac {C ^ { prime} left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right)} {C left ({ frac {q ^ {2}} { omega ^ {2}) }}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right)}}}$

Это показывает, что при просмотре уходящий На удаленных объектах наши инерциальные невращающиеся наблюдатели увидят, что их видимый размер изменяется точно так же, как расширение самого времениподобного геодезического сопоставления.

График Бринкмана

Один из способов быстро увидеть правдоподобие утверждения, что ты = ты₀ просто координатная сингулярность - напомнить, что наше пространство-время однородный, так что все события эквивалентны. Чтобы напрямую подтвердить это и изучить с другой точки зрения относительное движение наших инерциальных невращающихся наблюдателей, мы можем применить преобразование координат

${ displaystyle u to u}$

${ displaystyle v to v - { frac { dot {r}} {2r}} left (x ^ {2} + y ^ {2} right)}$

${ Displaystyle х к х / г}$

${ displaystyle y to y / r}$

где

${ displaystyle - { frac {{ ddot {r}} (u)} {r (u)}} = q sin ( omega u) ^ {2}}$

Это приводит решение к его представлению в терминах Координаты Бринкмана:

${ displaystyle ds ^ {2} = - q , sin ( omega u) ^ {2} , du ^ {2} -2 , du , dv + dx ^ {2} + dy ^ {2 }, qquad - infty$

Поскольку можно показать, что новые координаты геодезически полныйкоординаты Бринкмана определяют карта глобальных координат. На этом графике мы видим, что бесконечная последовательность из идентичный Циклы расширения-повторного сжатия происходят!

Каустики

В диаграмме Бринкмана наше поле кадра становится довольно сложным:

${ displaystyle { vec {e}} _ {0} = { frac { partial _ {u} + partial _ {v}} { sqrt {2}}} + left {{ frac { x ^ {2} + y ^ {2}} { sqrt {2}}} left (-q ^ {2} sin ( omega u) ^ {2} + { frac { omega ^ {2) }} {2}} , { frac {C ^ { prime} left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}) } {2 omega ^ {2}}}, omega u right) ^ {2}} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ {2}} {2 omega ^ {2}}}, omega u right) ^ {2}} right) partial _ {v} right } + left {{ frac { omega} {2}} { frac {C ^ { prime} left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac {q ^ { 2}} {2 omega ^ {2}}}, omega u right)} {C left ({ frac {q ^ {2}} { omega ^ {2}}}, { frac { q ^ {2}} {2 omega ^ {2}}}, omega u right)}} left (x partial _ {x} + y partial _ {y} right) right } }$

и так далее. Естественно, если мы вычислим тензор разложения, тензор электрогравитации и т. Д., Мы получим точно такие же ответы, как и раньше, но выраженные в новых координатах.

Поразительна простота метрического тензора по сравнению со сложностью фрейма. Дело в том, что нам легче визуализировать каустика формируется относительным движением наших наблюдателей на новой карте. Интегральные кривые времениподобного единичного геодезического векторного поля ${ displaystyle { vec {X}} = { vec {e}} _ {0}}$ дать мировые линии наших наблюдателей. На диаграмме Розена они отображаются в виде вертикальных координатных линий, поскольку эта диаграмма движется вместе.

Чтобы понять, как эта ситуация отображается на диаграмме Бринкмана, обратите внимание, что когда ω велико, наше времяподобное геодезическое единичное векторное поле становится приблизительно

${ displaystyle { vec {X}} приблизительно { frac { partial _ {u} + partial _ {v}} { sqrt {2}}} - q tan (qu) left (x partial _ {x} + y partial _ {y} right) + { frac {x ^ {2} + y ^ {2}} { sqrt {2}}} , left (-q ^ { 2} sin ( omega u) ^ {2} + q ^ {2} tan (qu) ^ {2} right) partial _ {v}}$

Подавляя последний член, имеем

Приблизительное движение нашей семьи наблюдателей, представленное на диаграмме Бринкмана

${ displaystyle { vec {X}} приблизительно partial _ {t} -q tan left ({ frac {qu} { sqrt {2}}} right) left (x partial _ { x} + y partial _ {y} right)}$

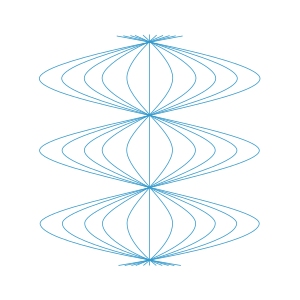
Мы немедленно получаем интегральную кривую, которая демонстрирует циклы синусоидального расширения и обратного схождения. Посмотрите на рисунок, на котором время течет вертикально, и мы используем радиальную симметрию, чтобы подавить одно пространственное измерение. На этом рисунке показано, почему на диаграмме Розена есть координатная сингулярность; наблюдатели должны фактически проходить мимо друг друга через равные промежутки времени, что явно несовместимо с сопутствующим свойством, поэтому диаграмма в этих местах ломается. Обратите внимание, что этот рисунок неправильно предполагает, что один наблюдатель является как бы «центром притяжения», но на самом деле они все полностью эквивалентны, из-за большой группы симметрии этого пространства-времени. Отметим также, что относительное движение наших наблюдателей в широком смысле синусоидальное полностью согласуется с поведением тензора разложения (относительно поля кадра, соответствующего нашему семейству наблюдателей), которое было отмечено выше.

Стоит отметить, что эти несколько хитрые моменты запутали фигуру не меньше, чем Альберт Эйнштейн в его статье 1937 года о гравитационных волнах (написанной задолго до того, как применяемый здесь современный математический аппарат получил широкое признание в физике).

Таким образом, на карте Бринкмана мировые линии наших наблюдателей в коротковолновом случае представляют собой периодические кривые, которые имеют форму синусоид с периодом ${ displaystyle 2 pi / q}$, модулированный гораздо меньшими синусоидальными возмущениями в нулевом направлении ∂_v и имея гораздо более короткий период, ${ displaystyle 2 pi / omega}$. Наблюдатели периодически расширяются и снова сжимаются поперек направления распространения; это движение модулируется короткопериодическими возмущениями малой амплитуды.

Резюме

Сравнивая наше точное решение с обычной монохроматической плоской электромагнитной волной, как описано в специальная теория относительности (т.е. как волна в плоском пространстве-времени, пренебрегая гравитационными эффектами энергии электромагнитного поля), мы видим, что поразительной новой особенностью общей теории относительности являются циклы расширения и схлопывания, испытываемые нашими наблюдателями, которые мы можем приписать кривизна фона, а не какие-либо измерения, сделанные на коротких временах и расстояниях (порядка длины волны электромагнитного излучения).

Смотрите также

• Аргумент липкой бусинки, за отчет о работе Эйнштейна и Розена 1937 года, упомянутой выше.

Рекомендации

• Миснер, Чарльз; Торн, Кип С. и Уиллер, Джон Арчибальд (1973). Гравитация. Сан-Франциско: В. Х. Фриман. ISBN 0-7167-0344-0. См. Раздел 35.11.