WikiDer > Общая теория относительности - Википедия

Часть цикла статей о
Общая теория относительности
${ displaystyle G _ { mu nu} + Lambda g _ { mu nu} = { frac {8 pi G} {c ^ {4}}} T _ { mu nu}}$
Вступление История Математическая формулировка Тесты
Основные концепции Принцип относительности Теория относительности Точка зрения Инерциальная система отсчета Рама отдыха Кадр с центром импульса Световой конус Принцип эквивалентности Эквивалентность массы и энергии Специальная теория относительности Двойная специальная теория относительности инвариант де Ситтера специальная теория относительности Масштаб относительности Мировая линия Подходящее время Риманова геометрия Энергетическое состояние
Явления Гравитоэлектромагнетизм Проблема Кеплера Сила тяжести Гравитационное поле Гравитационный колодец Гравитационное линзирование Гравитационные волны Гравитационное красное смещение Красное смещение Синее смещение Замедление времени Гравитационное замедление времени Задержка Шапиро Гравитационный потенциал Гравитационное сжатие Гравитационный коллапс Перетаскивание кадра Геодезический эффект Видимый горизонт Горизонт событий Гравитационная сингулярность Обнаженная особенность Черная дыра Белая дыра Пространство-время Космос Время Диаграммы пространства-времени Пространство-время Минковского Замкнутая времениподобная кривая (СТС) Червоточина Червоточина Эллиса
Уравнения Формализмы Уравнения Линеаризованная гравитация Уравнения поля Эйнштейна Фридман Геодезические Матиссон – Папапетру – Диксон Гамильтон – Якоби – Эйнштейн Инвариант кривизны (общая теория относительности) Лоренцево многообразие Формализмы ADM БССН Ньюман – Пенроуз Постньютоновский Продвинутая теория Теория Калуцы – Клейна Квантовая гравитация Супергравитация
Решения Шварцшильд (интерьер) Рейсснер-Нордстрём Гёдель Керр Керр – Ньюман Kasner Лемэтр – Толман Тауб-ОРЕХ Milne Робертсон – Уокер pp-волна van Stockum пыль Вейль – Льюис – Папапетру Вакуумный раствор
Теоремы Теорема Биркгофа Теорема Героха о расщеплении Теорема Гольдберга – Сакса. Теорема Лавлока Теорема об отсутствии волос Теоремы Пенроуза – Хокинга об особенностях Теорема положительной энергии
Ученые Эйнштейн Лоренц Гильберта Пуанкаре Шварцшильд де Ситтер Рейсснер Nordström Weyl Эддингтон Фридман Milne Цвикки Лемэтр Гёдель Уиллер Робертсон Бардин Уокер Керр Чандрасекхар Элерс Пенроуз Хокинг Райчаудхури Тейлор Hulse van Stockum Тауб Новичок Яу Торн другие
v т е

Воспроизвести медиа

Медленное компьютерное моделирование черной дыры бинарная система GW150914, как его видит ближайший наблюдатель, в течение 0,33 с после его последнего вдоха, слияния и посадки. Звездное поле за черными дырами сильно искажается и, кажется, вращается и перемещается из-за экстремальных гравитационное линзирование, так как пространство-время сам искажается и волочится вращающимся черные дыры.^[1]

Общая теория относительности, также известный как общая теория относительности, это геометрический теория из гравитация опубликовано Альберт Эйнштейн в 1915 году и является текущим описанием гравитации в современная физика. Общий относительность обобщает специальная теория относительности и уточняет Закон всемирного тяготения Ньютона, обеспечивая единое описание гравитации как геометрического свойства Космос и время или же четырехмерный пространство-время. В частности, кривизна пространства-времени напрямую связано с энергия и импульс чего бы то ни было иметь значение и радиация присутствуют. Отношение задается Уравнения поля Эйнштейна, система уравнения в частных производных.

Некоторые предсказания общей теории относительности значительно отличаются от предсказаний классическая физика, особенно с течением времени, геометрия пространства, движение тел в свободное падение, и распространение света. Примеры таких различий включают: гравитационное замедление времени, гравитационное линзирование, то гравитационное красное смещение света, гравитационное запаздывание и особенности/черные дыры. Предсказания общей теории относительности по отношению к классической физике были подтвержденный во всех наблюдениях и экспериментах на сегодняшний день. Хотя общая теория относительности не единственная релятивистская теория гравитации, это простейшая теория это соответствует экспериментальные данные. Однако остаются без ответа вопросы, самый фундаментальный из которых - как согласовать общую теорию относительности с законами квантовая физика создать полную и непротиворечивую теорию квантовая гравитациякак гравитация может быть единый с тремя негравитационными силами -сильный ядерный, слабый ядерный, и электромагнитный сила.

Теория Эйнштейна имеет важное астрофизический подразумеваемое. Например, это подразумевает существование черных дыр - областей пространства, в которых пространство и время искажены таким образом, что ничто, даже свет, не может ускользнуть, - как конечное состояние для массивные звезды. Существует множество свидетельств того, что сильное излучение, излучаемое некоторыми видами астрономических объектов, вызвано черными дырами. Например, микроквазары и активные галактические ядра в результате наличия звездные черные дыры и сверхмассивные черные дыры, соответственно. Искривление света под действием силы тяжести может привести к явлению гравитационного линзирования, при котором в небе видны несколько изображений одного и того же далекого астрономического объекта. Общая теория относительности также предсказывает существование гравитационные волны, которые с тех пор были наблюдается непосредственно коллаборацией физиков LIGO. Кроме того, общая теория относительности является основой современных космологический модели последовательно расширяющаяся вселенная.

Широко признанная теория необычайной красоты, общая теория относительности часто описывалась как самая красивая из всех существующих физических теорий.^[2]

История

Вскоре после публикации специальная теория относительности в 1905 году Эйнштейн начал думать о том, как включить сила тяжести в его новую релятивистскую структуру. В 1907 г., начав с простого мысленный эксперимент вовлекая наблюдателя в свободное падение, он приступил к поиску релятивистской теории гравитации, который длился восемь лет. После многочисленных обходных маневров и фальстартов его работа завершилась презентацией на Прусская Академия Наук в ноябре 1915 г. - то, что теперь известно как уравнения поля Эйнштейна, которые составляют основу общей теории относительности Эйнштейна.^[3] Эти уравнения определяют, как на геометрию пространства и времени влияют присутствующие материя и излучение.^[4] Математик 19 века Бернхард Риманнс неевклидова геометрия, называется Риманова геометрия, позволила Эйнштейну развить общую теорию относительности, предоставив ключевую математическую основу, на которой он соответствовал своим физическим представлениям о гравитации.^[5] На эту идею указал математик Марсель Гроссманн и опубликована Гроссманом и Эйнштейном в 1913 году.^[6]

Уравнения поля Эйнштейна: нелинейный и решить очень сложно. Эйнштейн использовал приближенные методы при разработке первоначальных предсказаний теории. Но в 1916 году астрофизик Карл Шварцшильд нашел первое нетривиальное точное решение уравнений поля Эйнштейна, Метрика Шварцшильда. Это решение заложило основу для описания заключительных стадий гравитационного коллапса и объектов, известных сегодня как черные дыры. В том же году были сделаны первые шаги к обобщению решения Шварцшильда на электрически заряженный были взяты объекты, в результате чего Решение Рейсснера – Нордстрема, который теперь связан с электрически заряженные черные дыры.^[7] В 1917 году Эйнштейн применил свою теорию к вселенная в целом, положив начало релятивистской космологии. В соответствии с современными представлениями, он предположил статическую Вселенную, добавив новый параметр к своим исходным уравнениям поля - космологическая постоянная- чтобы соответствовать этой наблюдательной презумпции.^[8] К 1929 г., однако, работа Хаббл и другие показали, что наша Вселенная расширяется. Это легко описывается расширяющимися космологическими решениями, найденными Фридман в 1922 г., которые не требуют космологической постоянной. Лемэтр использовали эти решения, чтобы сформулировать самую раннюю версию Большой взрыв модели, в которых наша Вселенная эволюционировала из чрезвычайно горячего и плотного более раннего состояния.^[9] Позднее Эйнштейн объявил космологическую постоянную самой большой ошибкой в ​​своей жизни.^[10]

В то время общая теория относительности оставалась чем-то вроде любопытства среди физических теорий. Он явно превосходил Ньютоновская гравитация, что согласуется со специальной теорией относительности и учитывает несколько эффектов, необъяснимых ньютоновской теорией. Эйнштейн показал в 1915 году, как его теория объясняла аномальное продвижение перигелия планеты Меркурий без произвольных параметров ("ложные факторы"),^[11] а в 1919 году экспедиция под руководством Эддингтон подтвердил предсказание общей теории относительности отклонения звездного света Солнцем в течение всего солнечное затмение 29 мая 1919 г.,^[12] мгновенно сделав Эйнштейна знаменитым.^[13] Тем не менее, теория оставалась вне основного направления теоретическая физика и астрофизика до развития примерно между 1960 и 1975 годами, теперь известная как золотой век общей теории относительности.^[14] Физики начали понимать концепцию черной дыры и идентифицировать квазары как одно из астрофизических проявлений этих объектов.^[15] Все более точные испытания солнечной системы подтвердили предсказательную силу теории.^[16] и релятивистская космология также стала доступной для прямых наблюдательных тестов.^[17]

За прошедшие годы общая теория относительности приобрела репутацию теории необычайной красоты.^[2][18][19] Субраманян Чандрасекар отметил, что на нескольких уровнях общая теория относительности демонстрирует то, что Френсис Бэкон назвал "странность в пропорции" (т.е.. элементы, вызывающие удивление и удивление). Он сопоставляет фундаментальные концепции (пространство и время против материя и движение), которые ранее считались полностью независимыми. Чандрасекар также отметил, что единственными руководителями Эйнштейна в его поисках точной теории были принцип эквивалентности и его понимание того, что правильное описание гравитации должно быть геометрическим в своей основе, так что существовал «элемент откровения» в том, как Эйнштейн пришел к своей теории.^[20] Другими элементами красоты, связанными с общей теорией относительности, являются ее простота и симметрия, способ, которым она включает инвариантность и унификацию, и ее совершенную логическую последовательность.^[21]

От классической механики к общей теории относительности

Общую теорию относительности можно понять, изучив ее сходство с классической физикой и отклонения от нее. Первым шагом является осознание того, что классическая механика и закон всемирного тяготения Ньютона допускают геометрическое описание. Сочетание этого описания с законами специальной теории относительности приводит к эвристическому выводу общей теории относительности.^[22]

Геометрия ньютоновской гравитации

Согласно общей теории относительности, объекты в гравитационном поле ведут себя так же, как объекты внутри ускоряющегося корпуса. Например, наблюдатель увидит, как мяч падает в ракете (слева), как и на Земле (справа), при условии, что ускорение ракеты равно 9,8 м / с.² (ускорение свободного падения на поверхности Земли).

В основе классическая механика это понятие, что телодвижение можно описать как комбинацию свободных (или инерционный) движение, и отклонения от этого свободного движения. Такие отклонения вызваны внешними силами, действующими на тело в соответствии с секундой Ньютона. закон движения, в котором говорится, что сеть сила действующее на тело равно инерциальному масса умноженный на ускорение.^[23] Предпочтительные инерционные движения связаны с геометрией пространства и времени: в стандартном системы отсчета Согласно классической механике, объекты в свободном движении движутся по прямым линиям с постоянной скоростью. Говоря современным языком, их пути геодезические, прямой мировые линии в искривленном пространстве-времени.^[24]

И наоборот, можно было бы ожидать, что инерционные движения, однажды идентифицированные путем наблюдения фактических движений тел и с учетом внешних сил (таких как электромагнетизм или же трение), может использоваться для определения геометрии пространства, а также времени координировать. Однако когда в игру вступает сила тяжести, возникает двусмысленность. Согласно закону всемирного тяготения Ньютона и независимо подтвержденным такими экспериментами, как эксперимент Eötvös и его преемники (см. Эксперимент Этвёша), существует универсальность свободного падения (также известного как слабое принцип эквивалентности, или всеобщее равенство инертной и пассивно-гравитационной масс): траектория движения тестовое тело в свободном падении зависит только от его положения и начальной скорости, но не от каких-либо свойств материала.^[25] Упрощенная версия этого воплощена в Эксперимент с лифтом Эйнштейна, проиллюстрированный на рисунке справа: для наблюдателя в небольшой замкнутой комнате он не может решить, отображая траекторию движения тел, например, упавшего шара, является ли комната неподвижной в гравитационном поле и мяч ускорение, или в свободном пространстве на борту ракеты, которая ускоряется со скоростью, равной скорости гравитационного поля по сравнению с шаром, который при выпуске не имеет ускорения.^[26]

Учитывая универсальность свободного падения, нет заметного различия между движением по инерции и движением под действием силы тяжести. Это предполагает определение нового класса инерционного движения, а именно движения объектов в свободном падении под действием силы тяжести. Этот новый класс предпочтительных движений также определяет геометрию пространства и времени - с математической точки зрения, это геодезическое движение, связанное с определенным связь что зависит от градиент из гравитационный потенциал. Пространство в этой конструкции все еще имеет обычное Евклидова геометрия. Однако пространствовремя в целом сложнее. Как можно показать с помощью простых мысленных экспериментов по траекториям свободного падения различных пробных частиц, результат переноса пространственно-временных векторов, которые могут обозначать скорость частицы (временноподобные векторы), будет изменяться в зависимости от траектории частицы; математически говоря, ньютоновская связь не интегрируемый. Отсюда можно сделать вывод, что пространство-время искривлено. Результирующий Теория Ньютона – Картана геометрическая формулировка ньютоновской гравитации, использующая только ковариантный концепции, то есть описание, действительное в любой желаемой системе координат.^[27] В этом геометрическом описании приливные эффекты- относительное ускорение тел при свободном падении - связаны с производной связи, показывая, как измененная геометрия вызвана наличием массы.^[28]

Релятивистское обобщение

Световой конус

Какой бы интригующей ни была геометрическая ньютоновская гравитация, ее основа, классическая механика, всего лишь предельный случай (специальной) релятивистской механики.^[29] На языке симметрия: там, где гравитацией можно пренебречь, физика Инвариант Лоренца как в специальной теории относительности, а не Инвариант Галилея как в классической механике. (Определяющей симметрией специальной теории относительности является Группа Пуанкаре, который включает в себя перемещения, вращения и ускорения.) Различия между ними становятся значительными при работе со скоростями, приближающимися к скорость света, и с явлениями высоких энергий.^[30]

При лоренцевой симметрии в игру вступают дополнительные структуры. Они определяются набором световых конусов (см. Изображение). Световые конусы определяют причинную структуру: для каждого мероприятие А, существует набор событий, на которые в принципе могут повлиять или на которые А через сигналы или взаимодействия, которые не должны двигаться быстрее света (например, событие B на изображении), и набор событий, для которых такое влияние невозможно (например, событие C на изображении). Эти наборы не зависят от наблюдателя.^[31] В сочетании с мировыми линиями свободно падающих частиц световые конусы могут использоваться для восстановления полуримановой метрики пространства-времени, по крайней мере, с точностью до положительного скалярного множителя. С математической точки зрения это определяет конформная структура^[32] или конформная геометрия.

Специальная теория относительности определяется в отсутствие гравитации, поэтому для практических приложений это подходящая модель, когда гравитацией можно пренебречь. Вводя в игру гравитацию и предполагая универсальность свободного падения, применимы те же рассуждения, что и в предыдущем разделе: нет глобальных инерциальные системы отсчета. Вместо этого есть приблизительные инерциальные системы отсчета, движущиеся вместе со свободно падающими частицами. В переводе на язык пространства-времени: прямой своевременный Линии, которые определяют инерциальную систему отсчета без гравитации, деформируются в линии, которые изогнуты относительно друг друга, предполагая, что включение гравитации требует изменения геометрии пространства-времени.^[33]

Априори не ясно, совпадают ли новые локальные системы отсчета при свободном падении с системами отсчета, в которых действуют законы специальной теории относительности - эта теория основана на распространении света и, следовательно, на электромагнетизме, который может иметь другой набор. предпочтительных кадров. Но, используя различные предположения о специальных релятивистских системах отсчета (например, они привязаны к Земле или находятся в свободном падении), можно получить разные прогнозы для гравитационного красного смещения, то есть того, как частота света смещается вместе с светом. распространяется через гравитационное поле (см. ниже). Фактические измерения показывают, что свободно падающие системы отсчета - это те, в которых распространяется свет, как в специальной теории относительности.^[34] Обобщение этого утверждения, а именно, что законы специальной теории относительности имеют хорошее приближение в свободно падающих (и невращающихся) системах отсчета, известно как Принцип эквивалентности Эйнштейна, важнейший руководящий принцип для обобщения специальной релятивистской физики с включением гравитации.^[35]

Те же экспериментальные данные показывают, что время, измеренное часами в гравитационном поле -подходящее время, выражаясь техническим термином, не следует правилам специальной теории относительности. На языке геометрии пространства-времени он не измеряется Метрика Минковского. Как и в случае с Ньютоном, это наводит на мысль о более общей геометрии. В малых масштабах все системы отсчета, находящиеся в свободном падении, эквивалентны и приблизительно соответствуют системе Минковского. Следовательно, мы имеем дело с криволинейным обобщением пространства Минковского. В метрический тензор которая определяет геометрию - в частности, как измеряются длины и углы - не является метрикой Минковского специальной теории относительности, это обобщение, известное как полу- или псевдориманов метрика. Кроме того, каждая риманова метрика естественным образом связана с одним конкретным типом связности, т.е. Леви-Чивита связь, и это, по сути, связь, удовлетворяющая принципу эквивалентности и делающая пространство локально минковским (т. е. подходящим локально инерциальные координаты, метрика Минковского, а ее первые частные производные и коэффициенты связности обращаются в нуль).^[36]

Уравнения Эйнштейна

После формулировки релятивистской геометрической версии эффектов гравитации остается вопрос об источнике гравитации. В ньютоновской гравитации источником является масса. В специальной теории относительности масса оказывается частью более общей величины, называемой тензор энергии-импульса, который включает как энергия и импульс плотности а также стресс: давление и сдвиг.^[37] Используя принцип эквивалентности, этот тензор легко обобщается на искривленное пространство-время. Продолжая далее аналогию с геометрической ньютоновской гравитацией, естественно предположить, что уравнение поля для гравитации связывает этот тензор и Тензор Риччи, который описывает особый класс приливных эффектов: изменение объема небольшого облака тестовых частиц, которые сначала находятся в состоянии покоя, а затем свободно падают. В специальной теории относительности сохранение энергии–Momentum соответствует утверждению, что тензор энергии-импульса равен расхождение-свободный. Эту формулу также легко обобщить на искривленное пространство-время, заменив частные производные на их искривленные -многообразие аналоги, ковариантные производные изучал дифференциальную геометрию. С этим дополнительным условием - ковариантная дивергенция тензора энергии-импульса и, следовательно, всего, что находится на другой стороне уравнения, равна нулю - простейшая система уравнений - это то, что называется (полевыми) уравнениями Эйнштейна:

Слева находится Тензор Эйнштейна, ${ Displaystyle G _ { mu nu}}$, которая является симметричной и конкретной бездивергентной комбинацией тензора Риччи ${ Displaystyle R _ { mu nu}}$ и метрика. Особенно,

${ Displaystyle R = g ^ { mu nu} R _ { mu nu} ,}$

- скаляр кривизны. Сам тензор Риччи относится к более общим Тензор кривизны Римана в качестве

${ displaystyle R _ { mu nu} = {R ^ { alpha}} _ { mu alpha nu}. ,}$

С правой стороны, ${ displaystyle T _ { mu nu}}$ - тензор энергии-импульса. Все тензоры записаны в обозначение абстрактного индекса.^[38] Согласование предсказания теории с результатами наблюдений для планетарный орбиты или, что то же самое, если гарантировать, что предел слабой гравитации и низкой скорости является ньютоновской механикой, константа пропорциональности оказывается равной ${ displaystyle { frac {8 pi G} {c ^ {4}}}}$, куда ${ displaystyle G}$ это гравитационная постоянная и ${ displaystyle c}$ скорость света в вакууме.^[39] Когда нет материи, так что тензор энергии-импульса обращается в нуль, результатом являются вакуумные уравнения Эйнштейна,

${ Displaystyle R _ { mu nu} = 0. ,}$

В общей теории относительности мировая линия частицы, свободные от всех внешних негравитационных сил, представляют собой особый тип геодезических в искривленном пространстве-времени. Другими словами, свободно движущаяся или падающая частица всегда движется по геодезической.

В геодезическое уравнение является:

${ displaystyle {d ^ {2} x ^ { mu} over ds ^ {2}} + Gamma ^ { mu} {} _ { alpha beta} {dx ^ { alpha} over ds } {dx ^ { beta} over ds} = 0,}$

куда ${ displaystyle s}$ - скалярный параметр движения (например, подходящее время), и ${ displaystyle Gamma ^ { mu} {} _ { alpha beta}}$ находятся Символы Кристоффеля (иногда называют аффинная связь коэффициенты или Леви-Чивита связь коэффициенты), который симметричен по двум нижним индексам. Греческие индексы могут принимать значения: 0, 1, 2, 3 и соглашение о суммировании используется для повторяющихся индексов ${ displaystyle alpha}$ и ${ displaystyle beta}$. Величина в левой части этого уравнения - это ускорение частицы, поэтому это уравнение аналогично Законы движения Ньютона которые также дают формулы для ускорения частицы. Это уравнение движения использует Обозначения Эйнштейна, что означает, что повторяющиеся индексы суммируются (то есть от нуля до трех). Символы Кристоффеля являются функциями четырех координат пространства-времени и поэтому не зависят от скорости, ускорения или других характеристик объекта. тестовая частица движение которого описывается уравнением геодезических.

Альтернативы общей теории относительности

Есть альтернативы общей теории относительности построены на тех же предпосылках, которые включают дополнительные правила и / или ограничения, приводящие к другим уравнениям поля. Примеры Теория Уайтхеда, Теория Бранса – Дике, телепараллелизм, ж(р) сила тяжести и Теория Эйнштейна – Картана.^[40]

Определение и основные приложения

Вывод, изложенный в предыдущем разделе, содержит всю информацию, необходимую для определения общей теории относительности, описания ее ключевых свойств и решения вопроса, имеющего решающее значение в физике, а именно, как теория может быть использована для построения моделей.

Определение и основные свойства

Общая теория относительности - это метрика теория гравитации. По своей сути Уравнения Эйнштейна, которые описывают связь между геометрией четырехмерного псевдориманово многообразие представляющий пространство-время, а энергия-импульс содержится в этом пространстве-времени.^[41] Явления, которые в классической механике приписываются действию силы тяжести (например, свободное падение, орбитальное движение, и космический корабль траектории), соответствуют инерционному движению в искривленной геометрии пространства-времени в общей теории относительности; нет гравитационной силы, отклоняющей объекты с их естественных прямых путей. Напротив, гравитация соответствует изменениям свойств пространства и времени, которые, в свою очередь, изменяют наиболее прямые пути, по которым естественным образом будут следовать объекты.^[42] Кривизна, в свою очередь, вызвана энергией-импульсом вещества. Перефразируя релятивиста Джон Арчибальд Уиллерпространство-время говорит, как двигаться; материя говорит пространству-времени, как искривляться.^[43]

Хотя общая теория относительности заменяет скаляр гравитационный потенциал классической физики симметричным классифицировать-два тензор, последнее сводится к первому в определенных предельные случаи. За слабые гравитационные поля и медленная скорость относительно скорости света предсказания теории сходятся с предсказаниями закона всемирного тяготения Ньютона.^[44]

Поскольку она построена с использованием тензоров, общая теория относительности показывает общая ковариация: его законы - и другие законы, сформулированные в общих релятивистских рамках - принимают одну и ту же форму во всех системы координат.^[45] Кроме того, теория не содержит никаких инвариантных геометрических фоновых структур, т.е. фон независимый. Таким образом, он удовлетворяет более строгим требованиям. общий принцип относительности, а именно, что законы физики одинаковы для всех наблюдателей.^[46] Локально, как выражено в принципе эквивалентности, пространство-время есть Минковский, а законы физики показывают локальная лоренц-инвариантность.^[47]

Построение модели

Ключевая концепция общерелятивистского построения моделей - это концепция решение уравнений Эйнштейна. Учитывая как уравнения Эйнштейна, так и подходящие уравнения для свойств материи, такое решение состоит из определенного полуриманова многообразия (обычно определяемого путем задания метрики в конкретных координатах) и конкретных полей материи, определенных на этом многообразии. Материя и геометрия должны удовлетворять уравнениям Эйнштейна, поэтому, в частности, тензор энергии-импульса материи должен быть бездивергентным. Материя, конечно, также должна удовлетворять любым дополнительным уравнениям, наложенным на ее свойства. Короче говоря, такое решение представляет собой модельную вселенную, которая удовлетворяет законам общей теории относительности и, возможно, дополнительным законам, регулирующим любую материю, которая может присутствовать.^[48]

Уравнения Эйнштейна являются нелинейными уравнениями с частными производными, и поэтому их трудно решить точно.^[49] Тем не менее, ряд точные решения известны, хотя лишь некоторые из них имеют прямое физическое применение.^[50] Наиболее известные точные решения, а также наиболее интересные с точки зрения физики, - это Решение Шварцшильда, то Решение Рейсснера – Нордстрема и Метрика Керра, каждая из которых соответствует определенному типу черной дыры в пустой вселенной,^[51] и Фридман – Лемэтр – Робертсон – Уокер и вселенные де Ситтера, каждая из которых описывает расширяющийся космос.^[52] Точные решения, представляющие большой теоретический интерес, включают Вселенная Гёделя (что открывает интригующую возможность путешествие во времени в искривленном пространстве-времени), Раствор Тауб-НУТ (модельная вселенная, однородный, но анизотропный), и пространство анти-де Ситтера (который недавно стал известен в контексте того, что называется Гипотеза Малдасены).^[53]

Учитывая сложность нахождения точных решений, уравнения поля Эйнштейна также часто решаются с помощью численное интегрирование на компьютере или рассматривая небольшие возмущения точных решений. В области числовая теория относительностимощные компьютеры используются для моделирования геометрии пространства-времени и решения уравнений Эйнштейна для интересных ситуаций, таких как две сталкивающиеся черные дыры.^[54] В принципе, такие методы могут применяться к любой системе при наличии достаточных компьютерных ресурсов и могут решать фундаментальные вопросы, такие как голые особенности. Приближенные решения также можно найти теории возмущений Такие как линеаризованная гравитация^[55] и его обобщение, постньютоновское расширение, оба из которых были разработаны Эйнштейном. Последний обеспечивает систематический подход к решению геометрии пространства-времени, которое содержит распределение материи, которое движется медленно по сравнению со скоростью света. Расширение включает в себя ряд терминов; первые члены представляют ньютоновскую гравитацию, тогда как более поздние члены представляют все меньшие поправки к теории Ньютона из-за общей теории относительности.^[56] Расширением этого расширения является параметризованный постньютоновский (PPN) формализм, который позволяет проводить количественные сравнения между предсказаниями общей теории относительности и альтернативными теориями.^[57]

Последствия теории Эйнштейна

Общая теория относительности имеет ряд физических последствий. Некоторые прямо вытекают из аксиом теории, тогда как другие стали ясны только в ходе многих лет исследований, последовавших за первоначальной публикацией Эйнштейна.

Гравитационное замедление времени и сдвиг частоты

Схематическое изображение гравитационного красного смещения световой волны, выходящей с поверхности массивного тела

Предполагая, что выполняется принцип эквивалентности,^[58] гравитация влияет на течение времени. Свет направлен в гравитационный колодец является голубоватый, тогда как свет, направленный в противоположном направлении (т. е. вылезающий из гравитационного колодца), красное смещение; В совокупности эти два эффекта известны как гравитационный сдвиг частоты. В более общем смысле, процессы, происходящие вблизи массивного тела, протекают медленнее по сравнению с процессами, происходящими дальше; этот эффект известен как гравитационное замедление времени.^[59]

Гравитационное красное смещение было измерено в лаборатории^[60] и используя астрономические наблюдения.^[61] Гравитационное замедление времени в гравитационном поле Земли измерялось много раз с помощью атомные часы,^[62] в то время как текущая проверка предоставляется как побочный эффект работы спутниковая система навигации (GPS).^[63] Испытания в более сильных гравитационных полях обеспечиваются наблюдением двойные пульсары.^[64] Все результаты согласуются с ОТО.^[65] Однако при нынешнем уровне точности эти наблюдения не могут отличить общую теорию относительности от других теорий, в которых действует принцип эквивалентности.^[66]

Отклонение света и гравитационная выдержка времени

Отклонение света (излучаемого из места, показанного синим) возле компактного тела (показано серым)

Общая теория относительности предсказывает, что путь света будет следовать кривизне пространства-времени, когда он проходит вблизи звезды. Первоначально этот эффект был подтвержден наблюдениями, как свет звезд или далеких квазаров отклонялся при прохождении солнце.^[67]

Это и связанные с ним предсказания вытекают из того факта, что свет следует за тем, что называется светоподобным или нулевая геодезическая- обобщение прямых линий, по которым движется свет в классической физике. Такие геодезические являются обобщением инвариантность скорости света в специальной теории относительности.^[68] При изучении подходящего модельного пространства-времени (либо внешнее решение Шварцшильда, либо, для более чем одной массы, постньютоновское расширение),^[69] проявляются несколько эффектов гравитации на распространение света. Хотя отклонение света также можно получить, расширив универсальность свободного падения на свет,^[70] угол отклонения, полученный в результате таких вычислений, составляет лишь половину значения, данного общей теорией относительности.^[71]

С отклонением света тесно связана гравитационная временная задержка (или задержка Шапиро), явление, при котором световым сигналам требуется больше времени для прохождения через гравитационное поле, чем в отсутствие этого поля. Это предсказание подверглось многочисленным успешным проверкам.^[72] в параметризованный постньютоновский формализм (PPN) измерения как отклонения света, так и гравитационной временной задержки определяют параметр, называемый γ, который кодирует влияние гравитации на геометрию пространства.^[73]

Гравитационные волны

Кольцо из пробных частиц, деформированное проходящей (линеаризованной, усиленной для лучшей видимости) гравитационной волной

Предсказано в 1916 году^[74][75] Согласно Альберту Эйнштейну, существуют гравитационные волны: рябь в метрике пространства-времени, которая распространяется со скоростью света. Это одна из нескольких аналогий между гравитацией слабого поля и электромагнетизмом в том смысле, что они аналогичны электромагнитные волны. 11 февраля 2016 года команда Advanced LIGO объявила, что у них есть непосредственно обнаруженные гравитационные волны из пара черных дыр слияние.^[76][77][78]

Простейший тип такой волны можно представить по ее действию на кольцо свободно плавающих частиц. Синусоидальная волна, распространяющаяся по такому кольцу к читателю, искажает кольцо характерным ритмичным образом (анимированное изображение справа).^[79] Поскольку уравнения Эйнштейна нелинейный, сколь угодно сильные гравитационные волны не подчиняются линейная суперпозиция, что затрудняет их описание. Однако линейные приближения гравитационных волн достаточно точны для описания чрезвычайно слабых волн, которые, как ожидается, прибудут сюда, на Землю, в результате далеких космических событий, которые обычно приводят к увеличению и уменьшению относительных расстояний на ${ displaystyle 10 ^ {- 21}}$ или менее. Методы анализа данных обычно используют тот факт, что эти линеаризованные волны могут быть Разложенный Фурье.^[80]

Некоторые точные решения описывают гравитационные волны без какого-либо приближения, например, волновой цуг, движущийся через пустое пространство.^[81] или же Безумные вселенные, разновидности расширяющегося космоса, наполненного гравитационными волнами.^[82] Но для гравитационных волн, возникающих в астрофизически значимых ситуациях, таких как слияние двух черных дыр, численные методы в настоящее время являются единственным способом построения соответствующих моделей.^[83]

Орбитальные эффекты и относительность направления

Общая теория относительности отличается от классической механики рядом предсказаний относительно движущихся по орбите тел. Он предсказывает общий поворот (прецессия) планетарных орбит, а также орбитальный распад, вызванный излучением гравитационных волн и эффектами, связанными с относительностью направления.

Прецессия апсид

Ньютоновская (красная) и эйнштейновская орбита (синяя) одинокой планеты, вращающейся вокруг звезды. Влияние других планет игнорируется.

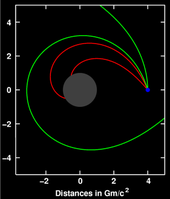
В общей теории относительности апсиды любой орбиты (точки наибольшего сближения орбитального тела с системой центр массы) буду прецессия; орбита не эллипс, но похоже на эллипс, который вращается в фокусе, в результате чего кривая розы-подобная форма (см. изображение). Эйнштейн впервые получил этот результат, используя приближенную метрику, представляющую ньютоновский предел, и рассматривая вращающееся тело как тестовая частица. По его мнению, тот факт, что его теория дала прямое объяснение аномального смещения перигелия Меркурия, обнаруженного ранее Урбен Леверье в 1859 г. стало важным свидетельством того, что он наконец определил правильную форму уравнений гравитационного поля.^[84]

Эффект также можно получить, используя точную метрику Шварцшильда (описывающую пространство-время вокруг сферической массы)^[85] или более общий постньютоновский формализм.^[86] Это связано с влиянием гравитации на геометрию пространства и вкладом собственная энергия к силе тяжести тела (закодированной в нелинейность уравнений Эйнштейна).^[87] Релятивистская прецессия наблюдалась для всех планет, которые позволяют проводить точные измерения прецессии (Меркурий, Венера и Земля),^[88] а также в двойных пульсарных системах, где он больше на пять порядки величины.^[89]

В ОТО сдвиг перигелия ${ displaystyle sigma}$, выраженное в радианах на оборот, приблизительно равно^[90]

${ displaystyle sigma = { frac {24 pi ^ {3} L ^ {2}} {T ^ {2} c ^ {2} (1-e ^ {2})}} ,}$

куда:

• ${ displaystyle L}$ это большая полуось
• ${ displaystyle T}$ это орбитальный период
• ${ displaystyle c}$ это скорость света в вакууме
• ${ displaystyle e}$ это орбитальный эксцентриситет

Орбитальный распад

Орбитальный распад для PSR1913 + 16: временной сдвиг в секундах, отслеживаемый на протяжении трех десятилетий.^[91]

Согласно общей теории относительности бинарная система будет излучать гравитационные волны, тем самым теряя энергию. Из-за этой потери расстояние между двумя орбитальными телами уменьшается, а вместе с ними и их период обращения. В рамках Солнечная система или для обычных двойные звезды, эффект слишком мал, чтобы его можно было наблюдать. Это не относится к тесной двойной системе пульсара, состоящей из двух движущихся по орбите. нейтронные звезды, один из которых пульсар: от пульсара наблюдатели на Земле получают регулярные серии радиоимпульсов, которые могут служить высокоточными часами, позволяющими точно измерять период обращения. Поскольку нейтронные звезды чрезвычайно компактны, значительное количество энергии испускается в виде гравитационного излучения.^[92]

Первое наблюдение уменьшения орбитального периода из-за излучения гравитационных волн было сделано Hulse и Тейлор, используя двойной пульсар PSR1913 + 16 они обнаружили в 1974 году. Это было первое обнаружение гравитационных волн, хотя и косвенное, за которое они были награждены премией 1993 года. Нобелевская премия по физике.^[93] С тех пор было найдено несколько других двойных пульсаров, в частности двойной пульсар. PSR J0737-3039, в котором обе звезды - пульсары.^[94]

Geodetic precession and frame-dragging

Several relativistic effects are directly related to the relativity of direction.^[95] Один geodetic precession: the axis direction of a гироскоп in free fall in curved spacetime will change when compared, for instance, with the direction of light received from distant stars—even though such a gyroscope represents the way of keeping a direction as stable as possible ("parallel transport").^[96] For the Moon–Earth system, this effect has been measured with the help of lunar laser ranging.^[97] More recently, it has been measured for test masses aboard the satellite Гравитационный зонд B to a precision of better than 0.3%.^[98][99]

Near a rotating mass, there are gravitomagnetic or перетаскивание кадра последствия. A distant observer will determine that objects close to the mass get "dragged around". This is most extreme for rotating black holes where, for any object entering a zone known as the ergosphere, rotation is inevitable.^[100] Such effects can again be tested through their influence on the orientation of gyroscopes in free fall.^[101] Somewhat controversial tests have been performed using the LAGEOS satellites, confirming the relativistic prediction.^[102] Так же Mars Global Surveyor probe around Mars has been used.^[103]

Astrophysical applications

Гравитационное линзирование

Einstein cross: four images of the same astronomical object, produced by a gravitational lens

The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing.^[104] Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an Кольцо Эйнштейна, or partial rings called arcs.^[105]В earliest example was discovered in 1979;^[106] since then, more than a hundred gravitational lenses have been observed.^[107] Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "микролинзирование events" have been observed.^[108]

Gravitational lensing has developed into a tool of наблюдательная астрономия. It is used to detect the presence and distribution of темная материя, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the Постоянная Хаббла. Statistical evaluations of lensing data provide valuable insight into the structural evolution of галактики.^[109]

Гравитационно-волновая астрономия

Artist's impression of the space-borne gravitational wave detector ЛИЗА

Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see Орбитальный распад, над). Detection of these waves is a major goal of current relativity-related research.^[110] Several land-based детекторы гравитационных волн are currently in operation, most notably the interferometric detectors GEO 600, LIGO (two detectors), TAMA 300 и ДЕВА.^[111] Разные временные матрицы пульсаров используют миллисекундные пульсары to detect gravitational waves in the 10⁻⁹ до 10⁻⁶ Герц frequency range, which originate from binary supermassive blackholes.^[112] A European space-based detector, eLISA / NGO, is currently under development,^[113] with a precursor mission (ЛИЗА Следопыт) having launched in December 2015.^[114]

Observations of gravitational waves promise to complement observations in the электромагнитный спектр.^[115] They are expected to yield information about black holes and other dense objects such as neutron stars and white dwarfs, about certain kinds of сверхновая звезда implosions, and about processes in the very early universe, including the signature of certain types of hypothetical cosmic string.^[116] In February 2016, the Advanced LIGO team announced that they had detected gravitational waves from a black hole merger.^[76][77][78]

Black holes and other compact objects

Simulation based on the equations of general relativity: a star collapsing to form a black hole while emitting gravitational waves

Whenever the ratio of an object's mass to its radius becomes sufficiently large, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of звездная эволюция, neutron stars of around 1.4 солнечные массы, and stellar black holes with a few to a few dozen solar masses, are thought to be the final state for the evolution of massive stars.^[117] Usually a galaxy has one supermassive black hole with a few million to a few миллиард solar masses in its center,^[118] and its presence is thought to have played an important role in the formation of the galaxy and larger cosmic structures.^[119]

Astronomically, the most important property of compact objects is that they provide a supremely efficient mechanism for converting gravitational energy into electromagnetic radiation.^[120] Аккреция, the falling of dust or gaseous matter onto stellar or supermassive black holes, is thought to be responsible for some spectacularly luminous astronomical objects, notably diverse kinds of active galactic nuclei on galactic scales and stellar-size objects such as microquasars.^[121] In particular, accretion can lead to релятивистские струи, focused beams of highly energetic particles that are being flung into space at almost light speed.^[122]General relativity plays a central role in modelling all these phenomena,^[123] and observations provide strong evidence for the existence of black holes with the properties predicted by the theory.^[124]

Black holes are also sought-after targets in the search for gravitational waves (cf. Гравитационные волны, над). Merging black hole binaries should lead to some of the strongest gravitational wave signals reaching detectors here on Earth, and the phase directly before the merger ("chirp") could be used as a "standard candle" to deduce the distance to the merger events–and hence serve as a probe of cosmic expansion at large distances.^[125] The gravitational waves produced as a stellar black hole plunges into a supermassive one should provide direct information about the supermassive black hole's geometry.^[126]

Космология

This blue horseshoe is a distant galaxy that has been magnified and warped into a nearly complete ring by the strong gravitational pull of the massive foreground luminous red galaxy.

The current models of cosmology are based on Полевые уравнения Эйнштейна, which include the cosmological constant ${ displaystyle Lambda}$ since it has important influence on the large-scale dynamics of the cosmos,

${displaystyle R_{mu u }-{ extstyle 1 over 2}R,g_{mu u }+Lambda g_{mu u }={frac {8pi G}{c^{4}}},T_{mu u }}$

куда ${displaystyle g_{mu u }}$ is the spacetime metric.^[127] Изотропный and homogeneous solutions of these enhanced equations, the Решения Фридмана – Лемэтра – Робертсона – Уокера.,^[128] allow physicists to model a universe that has evolved over the past 14 миллиард years from a hot, early Big Bang phase.^[129] Once a small number of parameters (for example the universe's mean matter density) have been fixed by astronomical observation,^[130] further observational data can be used to put the models to the test.^[131] Predictions, all successful, include the initial abundance of chemical elements formed in a period of primordial nucleosynthesis,^[132] the large-scale structure of the universe,^[133] and the existence and properties of a "тепловой echo" from the early cosmos, the космический фон.^[134]

Astronomical observations of the cosmological expansion rate allow the total amount of matter in the universe to be estimated, although the nature of that matter remains mysterious in part. About 90% of all matter appears to be dark matter, which has mass (or, equivalently, gravitational influence), but does not interact electromagnetically and, hence, cannot be observed directly.^[135] There is no generally accepted description of this new kind of matter, within the framework of known физика элементарных частиц^[136] or otherwise.^[137] Observational evidence from redshift surveys of distant supernovae and measurements of the cosmic background radiation also show that the evolution of our universe is significantly influenced by a cosmological constant resulting in an acceleration of cosmic expansion or, equivalently, by a form of energy with an unusual уравнение состояния, известный как темная энергия, the nature of which remains unclear.^[138]

An inflationary phase,^[139] an additional phase of strongly accelerated expansion at cosmic times of around 10⁻³³ seconds, was hypothesized in 1980 to account for several puzzling observations that were unexplained by classical cosmological models, such as the nearly perfect homogeneity of the cosmic background radiation.^[140] Recent measurements of the cosmic background radiation have resulted in the first evidence for this scenario.^[141] However, there is a bewildering variety of possible inflationary scenarios, which cannot be restricted by current observations.^[142] An even larger question is the physics of the earliest universe, prior to the inflationary phase and close to where the classical models predict the big bang необычность. An authoritative answer would require a complete theory of quantum gravity, which has not yet been developed^[143] (cf. the section on квантовая гравитация, ниже).

Путешествие во времени

Курт Гёдель показал^[144] that solutions to Einstein's equations exist that contain замкнутые времяподобные кривые (CTCs), which allow for loops in time. The solutions require extreme physical conditions unlikely ever to occur in practice, and it remains an open question whether further laws of physics will eliminate them completely. Since then, other—similarly impractical—GR solutions containing CTCs have been found, such as the Цилиндр Типлера и traversable wormholes.

Продвинутые концепции

Asymptotic symmetries

The spacetime symmetry group for Специальная теория относительности это Группа Пуанкаре, which is a ten-dimensional group of three Lorentz boosts, three rotations, and four spacetime translations. It is logical to ask what symmetries if any might apply in General Relativity. A tractable case might be to consider the symmetries of spacetime as seen by observers located far away from all sources of the gravitational field. The naive expectation for asymptotically flat spacetime symmetries might be simply to extend and reproduce the symmetries of flat spacetime of special relativity, а именно, the Poincaré group.

В 1962 г. Hermann Bondi, M. G. van der Burg, A. W. Metzner^[145] и Райнер К. Сакс^[146] addressed this asymptotic symmetry problem in order to investigate the flow of energy at infinity due to propagating гравитационные волны. Their first step was to decide on some physically sensible boundary conditions to place on the gravitational field at light-like infinity to characterize what it means to say a metric is asymptotically flat, making no априори assumptions about the nature of the asymptotic symmetry group — not even the assumption that such a group exists. Then after designing what they considered to be the most sensible boundary conditions, they investigated the nature of the resulting asymptotic symmetry transformations that leave invariant the form of the boundary conditions appropriate for asymptotically flat gravitational fields. What they found was that the asymptotic symmetry transformations actually do form a group and the structure of this group does not depend on the particular gravitational field that happens to be present. This means that, as expected, one can separate the kinematics of spacetime from the dynamics of the gravitational field at least at spatial infinity. The puzzling surprise in 1962 was their discovery of a rich infinite-dimensional group (the so-called BMS group) as the asymptotic symmetry group, instead of the finite-dimensional Poincaré group, which is a subgroup of the BMS group. Not only are the Lorentz transformations asymptotic symmetry transformations, there are also additional transformations that are not Lorentz transformations but are asymptotic symmetry transformations. In fact, they found an additional infinity of transformation generators known as supertranslations. This implies the conclusion that General Relativity (GR) does нет reduce to special relativity in the case of weak fields at long distances. It turns out that the BMS symmetry, suitably modified, could be seen as a restatement of the universal soft graviton theorem in квантовая теория поля (QFT), which relates universal infrared (soft) QFT with GR asymptotic spacetime symmetries.^[147]

Causal structure and global geometry

Penrose–Carter diagram of an infinite Minkowski universe

In general relativity, no material body can catch up with or overtake a light pulse. No influence from an event А can reach any other location Икс before light sent out at А к Икс. In consequence, an exploration of all light worldlines (нулевые геодезические) yields key information about the spacetime's causal structure. This structure can be displayed using Penrose–Carter diagrams in which infinitely large regions of space and infinite time intervals are shrunk ("уплотненный") so as to fit onto a finite map, while light still travels along diagonals as in standard spacetime diagrams.^[148]

Aware of the importance of causal structure, Роджер Пенроуз and others developed what is known as global geometry. In global geometry, the object of study is not one particular solution (or family of solutions) to Einstein's equations. Rather, relations that hold true for all geodesics, such as the Уравнение райчаудхури, and additional non-specific assumptions about the nature of matter (usually in the form of энергетические условия) are used to derive general results.^[149]

Горизонты

Using global geometry, some spacetimes can be shown to contain boundaries called горизонты, which demarcate one region from the rest of spacetime. The best-known examples are black holes: if mass is compressed into a sufficiently compact region of space (as specified in the гипотеза обруча, the relevant length scale is the Радиус Шварцшильда^[150]), no light from inside can escape to the outside. Since no object can overtake a light pulse, all interior matter is imprisoned as well. Passage from the exterior to the interior is still possible, showing that the boundary, the black hole's горизонт, is not a physical barrier.^[151]

The ergosphere of a rotating black hole, which plays a key role when it comes to extracting energy from such a black hole

Early studies of black holes relied on explicit solutions of Einstein's equations, notably the spherically symmetric Schwarzschild solution (used to describe a статический black hole) and the axisymmetric Решение Керра (used to describe a rotating, stationary black hole, and introducing interesting features such as the ergosphere). Using global geometry, later studies have revealed more general properties of black holes. With time they become rather simple objects characterized by eleven parameters specifying: electric charge, mass-energy, линейный импульс, angular momentum, and location at a specified time. This is stated by the black hole uniqueness theorem: "black holes have no hair", that is, no distinguishing marks like the hairstyles of humans. Irrespective of the complexity of a gravitating object collapsing to form a black hole, the object that results (having emitted gravitational waves) is very simple.^[152]

Even more remarkably, there is a general set of laws known as механика черной дыры, which is analogous to the законы термодинамики. For instance, by the second law of black hole mechanics, the area of the event horizon of a general black hole will never decrease with time, analogous to the энтропия термодинамической системы. This limits the energy that can be extracted by classical means from a rotating black hole (e.g. by the Процесс Пенроуза).^[153] There is strong evidence that the laws of black hole mechanics are, in fact, a subset of the laws of thermodynamics, and that the black hole area is proportional to its entropy.^[154] This leads to a modification of the original laws of black hole mechanics: for instance, as the second law of black hole mechanics becomes part of the second law of thermodynamics, it is possible for black hole area to decrease—as long as other processes ensure that, overall, entropy increases. As thermodynamical objects with non-zero temperature, black holes should emit тепловое излучение. Semi-classical calculations indicate that indeed they do, with the surface gravity playing the role of temperature in Закон планка. This radiation is known as Радиация Хокинга (ср. quantum theory section, ниже).^[155]

There are other types of horizons. In an expanding universe, an observer may find that some regions of the past cannot be observed ("particle horizon"), and some regions of the future cannot be influenced (event horizon).^[156] Even in flat Minkowski space, when described by an accelerated observer (Риндлер пространство), there will be horizons associated with a semi-classical radiation known as Унру радиация.^[157]

Особенности

Another general feature of general relativity is the appearance of spacetime boundaries known as singularities. Spacetime can be explored by following up on timelike and lightlike geodesics—all possible ways that light and particles in free fall can travel. But some solutions of Einstein's equations have "ragged edges"—regions known as spacetime singularities, where the paths of light and falling particles come to an abrupt end, and geometry becomes ill-defined. In the more interesting cases, these are "curvature singularities", where geometrical quantities characterizing spacetime curvature, such as the Скаляр Риччи, take on infinite values.^[158] Well-known examples of spacetimes with future singularities—where worldlines end—are the Schwarzschild solution, which describes a singularity inside an eternal static black hole,^[159] or the Kerr solution with its ring-shaped singularity inside an eternal rotating black hole.^[160] The Friedmann–Lemaître–Robertson–Walker solutions and other spacetimes describing universes have past singularities on which worldlines begin, namely Big Bang singularities, and some have future singularities (Big Crunch) также.^[161]

Given that these examples are all highly symmetric—and thus simplified—it is tempting to conclude that the occurrence of singularities is an artifact of idealization.^[162] Известный теоремы об особенностях, proved using the methods of global geometry, say otherwise: singularities are a generic feature of general relativity, and unavoidable once the collapse of an object with realistic matter properties has proceeded beyond a certain stage^[163] and also at the beginning of a wide class of expanding universes.^[164] However, the theorems say little about the properties of singularities, and much of current research is devoted to characterizing these entities' generic structure (hypothesized e.g. by the BKL conjecture).^[165] В гипотеза космической цензуры states that all realistic future singularities (no perfect symmetries, matter with realistic properties) are safely hidden away behind a horizon, and thus invisible to all distant observers. While no formal proof yet exists, numerical simulations offer supporting evidence of its validity.^[166]

Evolution equations

Each solution of Einstein's equation encompasses the whole history of a universe — it is not just some snapshot of how things are, but a whole, possibly matter-filled, spacetime. It describes the state of matter and geometry everywhere and at every moment in that particular universe. Due to its general covariance, Einstein's theory is not sufficient by itself to determine the эволюция во времени of the metric tensor. It must be combined with a coordinate condition, which is analogous to крепление датчика in other field theories.^[167]

To understand Einstein's equations as partial differential equations, it is helpful to formulate them in a way that describes the evolution of the universe over time. This is done in "3+1" formulations, where spacetime is split into three space dimensions and one time dimension. Самый известный пример - это Формализм ADM.^[168] These decompositions show that the spacetime evolution equations of general relativity are well-behaved: solutions always существовать, and are uniquely defined, once suitable initial conditions have been specified.^[169] Such formulations of Einstein's field equations are the basis of numerical relativity.^[170]

Global and quasi-local quantities

The notion of evolution equations is intimately tied in with another aspect of general relativistic physics. In Einstein's theory, it turns out to be impossible to find a general definition for a seemingly simple property such as a system's total mass (or energy). The main reason is that the gravitational field—like any physical field—must be ascribed a certain energy, but that it proves to be fundamentally impossible to localize that energy.^[171]

Nevertheless, there are possibilities to define a system's total mass, either using a hypothetical "infinitely distant observer" (Масса ADM)^[172] or suitable symmetries (Комарская масса).^[173] If one excludes from the system's total mass the energy being carried away to infinity by gravitational waves, the result is the Bondi mass в нулевой бесконечности.^[174] Как и в классическая физика, it can be shown that these masses are positive.^[175] Corresponding global definitions exist for momentum and angular momentum.^[176] There have also been a number of attempts to define квазилокальный quantities, such as the mass of an isolated system formulated using only quantities defined within a finite region of space containing that system. The hope is to obtain a quantity useful for general statements about изолированные системы, such as a more precise formulation of the hoop conjecture.^[177]

Relationship with quantum theory

If general relativity were considered to be one of the two pillars of modern physics, then quantum theory, the basis of understanding matter from elementary particles to физика твердого тела, would be the other.^[178] However, how to reconcile quantum theory with general relativity is still an open question.

Квантовая теория поля в искривленном пространстве-времени

Обычный квантовые теории поля, which form the basis of modern elementary particle physics, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth.^[179] In order to describe situations in which gravity is strong enough to influence (quantum) matter, yet not strong enough to require quantization itself, physicists have formulated quantum field theories in curved spacetime. These theories rely on general relativity to describe a curved background spacetime, and define a generalized quantum field theory to describe the behavior of quantum matter within that spacetime.^[180] Using this formalism, it can be shown that black holes emit a blackbody spectrum of particles known as Радиация Хокинга leading to the possibility that they испариться через некоторое время.^[181] As briefly mentioned над, this radiation plays an important role for the thermodynamics of black holes.^[182]

Квантовая гравитация

The demand for consistency between a quantum description of matter and a geometric description of spacetime,^[183] as well as the appearance of singularities (where curvature length scales become microscopic), indicate the need for a full theory of quantum gravity: for an adequate description of the interior of black holes, and of the very early universe, a theory is required in which gravity and the associated geometry of spacetime are described in the language of quantum physics.^[184] Despite major efforts, no complete and consistent theory of quantum gravity is currently known, even though a number of promising candidates exist.^[185][186]

Projection of a Многообразие Калаби – Яу, one of the ways of compactifying the extra dimensions posited by string theory

Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems.^[187] Some have argued that at low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity.^[188] At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative non-renormalizability").^[189]

Простой spin network of the type used in loop quantum gravity

One attempt to overcome these limitations is теория струн, a quantum theory not of точечные частицы, but of minute one-dimensional extended objects.^[190] The theory promises to be a unified description of all particles and interactions, including gravity;^[191] the price to pay is unusual features such as six дополнительные размеры of space in addition to the usual three.^[192] В том, что называется вторая суперструнная революция, it was conjectured that both string theory and a unification of general relativity and суперсимметрия известный как supergravity^[193] form part of a hypothesized eleven-dimensional model known as М-теория, which would constitute a uniquely defined and consistent theory of quantum gravity.^[194]

Another approach starts with the каноническое квантование procedures of quantum theory. Using the initial-value-formulation of general relativity (cf. evolution equations above), the result is the Wheeler–deWitt equation (an analogue of the Уравнение Шредингера) which, regrettably, turns out to be ill-defined without a proper ultraviolet (lattice) cutoff.^[195] However, with the introduction of what are now known as Переменные Аштекара,^[196] this leads to a promising model known as петля квантовой гравитации. Space is represented by a web-like structure called a spin network, evolving over time in discrete steps.^[197]

Depending on which features of general relativity and quantum theory are accepted unchanged, and on what level changes are introduced,^[198] there are numerous other attempts to arrive at a viable theory of quantum gravity, some examples being the lattice theory of gravity based on the Feynman Path Integral approach and Regge Calculus,^[185] dynamical triangulations,^[199] causal sets,^[200] twistor models^[201] or the path integral based models of quantum cosmology.^[202]

All candidate theories still have major formal and conceptual problems to overcome. They also face the common problem that, as yet, there is no way to put quantum gravity predictions to experimental tests (and thus to decide between the candidates where their predictions vary), although there is hope for this to change as future data from cosmological observations and particle physics experiments becomes available.^[203]

Текущее состояние

Observation of gravitational waves from binary black hole merger GW150914

General relativity has emerged as a highly successful model of gravitation and cosmology, which has so far passed many unambiguous observational and experimental tests. However, there are strong indications the theory is incomplete.^[204] The problem of quantum gravity and the question of the reality of spacetime singularities remain open.^[205] Observational data that is taken as evidence for dark energy and dark matter could indicate the need for new physics.^[206] Even taken as is, general relativity is rich with possibilities for further exploration. Mathematical relativists seek to understand the nature of singularities and the fundamental properties of Einstein's equations,^[207] while numerical relativists run increasingly powerful computer simulations (such as those describing merging black holes).^[208] In February 2016, it was announced that the existence of gravitational waves was directly detected by the Advanced LIGO team on September 14, 2015.^{[78][209][210]} A century after its introduction, general relativity remains a highly active area of research.^[211]

Смотрите также

Примечания

Рекомендации

дальнейшее чтение

Популярные книги

• Эйнштейн, А. (1916), Относительность: специальная и общая теория, Берлин, ISBN 978-3-528-06059-6
• Героч, Р. (1981), Общая теория относительности от А до Б, Чикаго: Издательство Чикагского университета, ISBN 978-0-226-28864-2
• Либер, Лилиан (2008), Теория относительности Эйнштейна: путешествие в четвертое измерение, Филадельфия: Paul Dry Books, Inc., ISBN 978-1-58988-044-3
• Шутц, Бернард Ф. (2001), «Гравитационное излучение», в Murdin, Paul (ed.), Энциклопедия астрономии и астрофизики, ISBN 978-1-56159-268-5
• Торн, Кип; Хокинг, Стивен (1994). Черные дыры и искажения времени: возмутительное наследие Эйнштейна. Нью-Йорк: У. В. Нортон. ISBN 0393035050.
• Вальд, Роберт М. (1992), Пространство, время и гравитация: теория большого взрыва и черных дыр, Чикаго: Издательство Чикагского университета, ISBN 978-0-226-87029-8
• Уиллер, Джон; Форд, Кеннет (1998), Геоны, черные дыры и квантовая пена: жизнь в физике, Нью-Йорк: W. W. Norton, ISBN 978-0-393-31991-0

Учебники для начинающих бакалавриата

• Каллахан, Джеймс Дж. (2000), Геометрия пространства-времени: введение в специальную и общую теорию относительности, Нью-Йорк: Springer, ISBN 978-0-387-98641-8
• Тейлор, Эдвин Ф .; Уиллер, Джон Арчибальд (2000), Изучение черных дыр: введение в общую теорию относительности, Эддисон Уэсли, ISBN 978-0-201-38423-9

Учебники для бакалавриата

• Ченг, Та-пей (2005), Относительность, гравитация и космология: базовое введение, Оксфорд и Нью-Йорк: Издательство Оксфордского университета, ISBN 978-0-19-852957-6
• Дирак, Поль (1996), Общая теория относительности, Издательство Принстонского университета, ISBN 978-0-691-01146-2
• Gron, O .; Хервик, С. (2007), Общая теория относительности Эйнштейна, Спрингер, ISBN 978-0-387-69199-2
• Хартл, Джеймс Б. (2003), Гравитация: введение в общую теорию относительности Эйнштейна, Сан-Франциско: Аддисон-Уэсли, ISBN 978-0-8053-8662-2
• Хьюстон, Л. П.; Тод, К. П. (1991), Введение в общую теорию относительности, Кембридж: Издательство Кембриджского университета, ISBN 978-0-521-33943-8
• д'Инверно, Рэй (1992), Введение в теорию относительности Эйнштейна, Оксфорд: Издательство Оксфордского университета, ISBN 978-0-19-859686-8
• Людык, Гюнтер (2013). Эйнштейн в матричной форме (1-е изд.). Берлин: Springer. ISBN 978-3-642-35797-8.
• Мёллер, Кристиан (1955) [1952], Теория относительности, Издательство Оксфордского университета, OCLC 7644624
• Мур, Томас А (2012), Рабочая тетрадь по общей теории относительности, Университетские научные книги, ISBN 978-1-891389-82-5
• Шютц, Б. Ф. (2009), Первый курс общей теории относительности (Второе изд.), Cambridge University Press, ISBN 978-0-521-88705-2

Учебники для выпускников

• Кэрролл, Шон М. (2004), Пространство-время и геометрия: введение в общую теорию относительности, Сан-Франциско: Аддисон-Уэсли, ISBN 978-0-8053-8732-2
• Грён, Эйвинд; Хервик, Сигбьёрн (2007), Общая теория относительности Эйнштейна, Нью-Йорк: Springer, ISBN 978-0-387-69199-2
• Ландау, Лев Д.; Лифшиц, Евгений Федорович (1980), Классическая теория поля (4-е изд.), Лондон: Баттерворт-Хайнеманн, ISBN 978-0-7506-2768-9
• Стефани, Ганс (1990), Общая теория относительности: введение в теорию гравитационного поля, Кембридж: Издательство Кембриджского университета, ISBN 978-0-521-37941-0
• Уилл, Клиффорд; Пуассон, Эрик (2014). Гравитация: ньютоновская, постньютоновская, релятивистская. Издательство Кембриджского университета. ISBN 978-1107032866.

Книги специалистов

• Хокинг, Стивен; Эллис, Джордж (1975). Крупномасштабная структура пространства-времени. Издательство Кембриджского университета. ISBN 978-0521099066.
• Пуассон, Эрик (2007). Инструментарий релятивиста: математика механики черной дыры. Издательство Кембриджского университета. ISBN 978-0521537803.

журнальные статьи

• Эйнштейн, Альберт (1916), "Die Grundlage der allgemeinen Relativitätstheorie", Annalen der Physik, 49 (7): 769–822, Bibcode:1916AnP ... 354..769E, Дои:10.1002 / andp.19163540702 Смотрите также Английский перевод в Einstein Papers Project
• Фланаган, Эанна Э .; Хьюз, Скотт А. (2005), "Основы теории гравитационных волн", New J. Phys., 7 (1): 204, arXiv:gr-qc / 0501041, Bibcode:2005NJPh .... 7..204F, Дои:10.1088/1367-2630/7/1/204
• Ландграф, М .; Hechler, M .; Кембл, С. (2005), "Дизайн миссии для LISA Pathfinder", Учебный класс. Квантовая гравитация., 22 (10): S487 – S492, arXiv:gr-qc / 0411071, Bibcode:2005CQGra..22S.487L, Дои:10.1088/0264-9381/22/10/048
• Ньето, Майкл Мартин (2006), «Стремление понять аномалию Пионеров» (PDF), Новости Europhysics, 37 (6): 30–34, arXiv:gr-qc / 0702017, Bibcode:2006ENews..37f..30N, Дои:10.1051 / epn: 2006604
• Шапиро, И.И.; Петтенгилл, Гордон; Эш, Майкл; Стоун, Мелвин; Смит, Уильям; Ингаллс, Ричард; Брокельман, Ричард (1968), «Четвертый тест общей теории относительности: предварительные результаты», Phys. Rev. Lett., 20 (22): 1265–1269, Bibcode:1968ПхРвЛ..20.1265С, Дои:10.1103 / PhysRevLett.20.1265
• Валтонен, М. Дж .; Lehto, H.J .; Nilsson, K .; Heidt, J .; Takalo, L.O .; Силланпяя, А .; Виллфорт, С .; Kidger, M .; и другие. (2008), «Массивная двойная система черных дыр в OJ 287 и проверка общей теории относительности», Природа, 452 (7189): 851–853, arXiv:0809.1280, Bibcode:2008Натура.452..851В, Дои:10.1038 / природа06896, PMID 18421348

внешняя ссылка

Викискладе есть медиафайлы по теме Общая теория относительности.

В Викиучебнике есть больше по темам: Общая теория относительности

В Викиверситете есть учебные ресурсы о Общая теория относительности

В Wikisource есть оригинальные работы по теме: Относительность

Wikisource есть оригинальный текст, относящийся к этой статье: Относительность: специальная и общая теория

• Эйнштейн онлайн - Статьи по различным аспектам релятивистской физики для широкой аудитории; организовано Институт Макса Планка гравитационной физики
• Домашняя страница GEO600, официальный сайт проекта GEO600.
• Лаборатория LIGO
• Морщины NCSA Spacetime - произведено группой численной теории относительности NCSA, с элементарным введением в общую теорию относительности

• Общая теория относительности Эйнштейна на YouTube (лекция Леонард Сасскинд записано 22 сентября 2008 г. в Стэндфордский Университет).
• Цикл лекций по общей теории относительности выданный в 2006 г. на Institut Henri Poincaré (вводный / продвинутый).
• Учебники по общей теории относительности к Джон Баэз.
• Браун, Кевин. «Размышления об относительности». Mathpages.com. Архивировано из оригинал 18 декабря 2015 г.. Получено 29 мая 2005.
• Кэрролл, Шон М. (1997). «Конспект лекций по общей теории относительности». arXiv:gr-qc / 9712019.
• Мур, Рафи. «Понимание общей теории относительности». Получено 11 июля 2006.
• Ванер, Стефан. «Введение в дифференциальную геометрию и общую теорию относительности» (PDF). Получено 5 апреля 2015.