WikiDer > Сила тяжести
| Часть серии по |
| Классическая механика |
|---|
Основные темы |
Категории |
Сила тяжести (из латинский авторитет 'масса'[1]), или же гравитация, это естественное явление которым все с масса или же энергия-включая планеты, звезды, галактики, и даже свет[2]- приводятся к (или притягиваться навстречу друг другу. На земной шар, гравитация дает масса к физические объекты, а Лунас сила тяжести вызывает океан приливы. Гравитационное притяжение исходного газового вещества, присутствующего в Вселенная заставил это начаться слияние и формирование звезд и заставил звезды группироваться в галактики, поэтому гравитация ответственна за многие крупномасштабные структуры во Вселенной. Гравитация имеет бесконечный диапазон, хотя ее эффекты становятся все слабее по мере удаления объектов.
Гравитацию наиболее точно описывает общая теория относительности (предложено Альберт Эйнштейн в 1915 г.), который описывает гравитацию не как силу, а как следствие движения масс "прямо вперед" в искривленное пространство-время вызвано неравномерным распределением массы. Самый крайний пример этой кривизны пространства-времени - это черная дыра, из которой ничто - даже свет - не может ускользнуть, пройдя мимо черной дыры горизонт событий.[3] Однако для большинства приложений гравитация хорошо аппроксимируется Закон всемирного тяготения Ньютона, который описывает гравитацию как сила заставляя любые два тела притягиваться друг к другу с величиной пропорциональный к продукту их массы и обратно пропорциональный к квадрат из расстояние между ними.
Гравитация - самая слабая из четырех фундаментальные взаимодействия физики, примерно 1038 раз слабее, чем сильное взаимодействие, 1036 раз слабее, чем электромагнитная сила и 1029 раз слабее, чем слабое взаимодействие. Как следствие, он не имеет существенного влияния на уровне субатомных частиц.[4] Напротив, это доминирующее взаимодействие на макроскопический масштаб, и является причиной образования, формы и траектория (орбита) из астрономические тела.
Текущие модели физика элементарных частиц подразумевают, что самый ранний случай гравитации во Вселенной, возможно, в форме квантовая гравитация, супергравитация или гравитационная сингулярностьнаряду с обычными Космос и время, разработанные в Эпоха Планка (до 10−43 секунд после рождение Вселенной), возможно, из первобытного состояния, такого как ложный вакуум, квантовый вакуум или же виртуальная частица, неизвестным в настоящее время способом.[5] Попытки разработать теорию гравитации в соответствии с квантовая механика, а квантовая гравитация теория, которая позволила бы объединить гравитацию в общую математическую структуру ( теория всего) с тремя другими фундаментальными взаимодействиями физики, являются текущей областью исследований.
История теории гравитации
Древний мир
Древнегреческий философ Архимед обнаружил центр гравитации треугольника.[6] Он также предположил, что если бы у двух одинаковых гирь не был одинаковый центр тяжести, центр тяжести двух гирь вместе был бы посередине линии, соединяющей их центры тяжести.[7]
Римский архитектор и инженер Витрувий в De Architectura постулировал, что сила тяжести объекта зависит не от веса, а от его «природы».[8]
В древней Индии Арьябхата сначала определили силу, чтобы объяснить, почему объекты не выбрасываются наружу при вращении Земли. Брахмагупта описал гравитацию как силу притяжения и использовал термин «гурутваакаршан» для обозначения гравитации.[9][10]
Научная революция
Современные работы по теории гравитации начались с работ Галилео Галилей в конце 16 - начале 17 вв. В его знаменитом (хотя, возможно, апокрифический[11]) экспериментируйте, бросая шары из Пизанская башня, а затем с тщательными измерениями скатывающихся шариков склоныГалилей показал, что ускорение свободного падения одинаково для всех объектов. Это было серьезным отклонением от Аристотельвера в то, что более тяжелые объекты имеют большее ускорение свободного падения.[12] Галилей постулировал сопротивление воздуха как причина того, что объекты с меньшей массой медленнее падают в атмосфере. Работа Галилея заложила основу для формулировки теории гравитации Ньютона.[13]
Теория тяготения Ньютона

В 1687 году английский математик сэр Исаак Ньютон опубликовано Principia, что предполагает закон обратных квадратов всемирного тяготения. По его собственным словам, «я пришел к выводу, что силы, удерживающие планеты в их орбах, должны [быть] обратно пропорциональны квадратам их расстояний от центров, вокруг которых они вращаются: и таким образом сравнил силу, необходимую для удержания Луны в ее сфере. с силой тяжести на поверхности Земли, и нашел их ответ почти.[14] Уравнение следующее:
Где F это сила, м1 и м2 - массы взаимодействующих объектов, р расстояние между центрами масс и грамм это гравитационная постоянная.
Теория Ньютона пользовалась наибольшим успехом, когда ее использовали для предсказания существования Нептун на основе движений Уран это не могло быть объяснено действиями других планет. Расчеты обоих Джон Коуч Адамс и Урбен Леверье предсказал общее положение планеты, и расчеты Леверье привели Иоганн Готфрид Галле к открытию Нептуна.
Несоответствие в МеркурийОрбита России указала на недостатки теории Ньютона. К концу 19 века стало известно, что на его орбите наблюдаются небольшие возмущения, которые нельзя полностью объяснить теорией Ньютона, но все поиски другого возмущающего тела (например, планеты, вращающейся вокруг Солнца, даже более близкой, чем Меркурий), были бесплодно. Вопрос был решен в 1915 г. Альберт Эйнштейнновая теория общая теория относительности, что объясняет небольшое расхождение орбиты Меркурия. Это несоответствие было продвижением перигелий Меркурия 42,98 угловой секунды в столетие.[15]
Хотя теория Ньютона была заменена общей теорией относительности Альберта Эйнштейна, большинство современных нерелятивистский гравитационные расчеты по-прежнему производятся с использованием теории Ньютона, потому что с ней проще работать и она дает достаточно точные результаты для большинства приложений, включающих достаточно малые массы, скорости и энергии.
Принцип эквивалентности
В принцип эквивалентности, исследованный рядом исследователей, включая Галилео, Лоранд Этвеш, и Эйнштейн, выражает идею о том, что все объекты падают одинаково, и что эффекты гравитации неотличимы от определенных аспектов ускорения и замедления. Самый простой способ проверить принцип слабой эквивалентности - бросить два объекта разной массы или состава в вакуум и посмотреть, упадут ли они на землю одновременно. Такие эксперименты демонстрируют, что все объекты падают с одинаковой скоростью, когда другие силы (например, сопротивление воздуха и электромагнитные эффекты) незначительны. В более сложных испытаниях используются крутильные весы, изобретенные Этвешем. Спутниковые эксперименты, например ШАГ, предназначены для более точных экспериментов в космосе.[16]
Формулировки принципа эквивалентности включают:
- Принцип слабой эквивалентности: Траектория точечной массы в гравитационное поле зависит только от его начального положения и скорости и не зависит от его состава.[17]
- Принцип эквивалентности Эйнштейна: Результат любого локального негравитационного эксперимента в свободно падающей лаборатории не зависит от скорости лаборатории и ее местоположения в пространстве-времени.[18]
- Принцип строгой эквивалентности, требующий и того, и другого.
Общая теория относительности
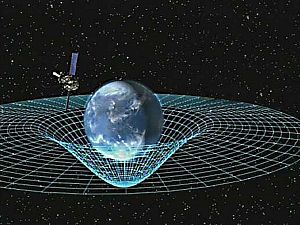
В общая теория относительности, эффекты гравитации приписываются пространство-время кривизна вместо силы. Отправной точкой общей теории относительности является принцип эквивалентности, который приравнивает свободное падение к инерционному движению и описывает свободно падающие инерционные объекты как ускоряющиеся относительно неинерциальных наблюдателей на земле.[19][20] В Ньютоновская физикаоднако такое ускорение не может произойти, если хотя бы один из объектов не подвергается действию силы.
Эйнштейн предположил, что пространство-время искривляется материей и что свободно падающие объекты движутся по локально прямым траекториям в искривленном пространстве-времени. Эти прямые пути называются геодезические. Как и первый закон движения Ньютона, теория Эйнштейна утверждает, что если к объекту приложить силу, он отклонится от геодезической. Например, мы больше не следуем геодезическим, стоя, потому что механическое сопротивление Земли оказывает на нас восходящую силу, и в результате мы не инерционны на земле. Это объясняет, почему движение по геодезическим в пространстве-времени считается инерционным.
Эйнштейн открыл уравнения поля общей теории относительности, которые связывают наличие материи и кривизну пространства-времени и названы в его честь. В Уравнения поля Эйнштейна набор из 10 одновременный, нелинейный, дифференциальные уравнения. Решения уравнений поля являются составляющими метрический тензор пространства-времени. Метрический тензор описывает геометрию пространства-времени. Геодезические пути для пространства-времени вычисляются из метрического тензора.
Решения
Известные решения уравнений поля Эйнштейна включают:
- В Решение Шварцшильда, который описывает пространство-время, окружающее сферически симметричный не-вращающийся незаряженный массивный объект. Для достаточно компактных объектов это решение генерировало черная дыра с центральным необычность. Для радиальных расстояний от центра, которые намного больше, чем Радиус Шварцшильда, ускорения, предсказанные решением Шварцшильда, практически идентичны тем, которые предсказывает теория гравитации Ньютона.
- В Решение Reissner-Nordström, в котором центральный объект имеет электрический заряд. Для сборов с геометризованный длины, которые меньше геометрической длины массы объекта, это решение создает черные дыры с двойным горизонты событий.
- В Решение Керра для вращения массивных предметов. Это решение также создает черные дыры с несколькими горизонтами событий.
- В Решение Керра-Ньюмана для заряженных вращающихся массивных объектов. Это решение также создает черные дыры с несколькими горизонтами событий.
- В космологический Решение Фридмана-Лемэтра-Робертсона-Уокера, предсказывающий расширение Вселенной.
Тесты
В тесты общей теории относительности включали следующее:[21]
- Общая теория относительности объясняет аномальный прецессия перигелия Меркурия.[22]
- Прогноз, что время течет медленнее при более низких потенциалах (гравитационное замедление времени) был подтвержден Эксперимент Паунда – Ребки (1959), Эксперимент Хафеле – Китинга, а GPS.
- Предсказание об отклонении света было впервые подтверждено Артур Стэнли Эддингтон из его наблюдений во время Солнечное затмение 29 мая 1919 г..[23][24] Эддингтон измерил отклонения звездного света вдвое больше, чем предсказывает корпускулярная теория Ньютона, в соответствии с предсказаниями общей теории относительности. Однако его интерпретация результатов позже была оспорена.[25] Более поздние испытания с использованием радиоинтерферометрических измерений квазары проходящие за Солнцем более точно и последовательно подтвердили отклонение света в степени, предсказанной общей теорией относительности.[26] Смотрите также гравитационная линза.
- В время задержки света проходящий близко к массивному объекту был впервые идентифицирован Ирвин И. Шапиро в 1964 г. по сигналам межпланетных космических аппаратов.
- Гравитационное излучение косвенно подтверждено исследованиями двоичных пульсары. 11 февраля 2016 г. LIGO и Дева коллаборации объявили о первом наблюдении гравитационной волны.
- Александр Фридманн в 1922 г. обнаружил, что уравнения Эйнштейна имеют нестационарные решения (даже при наличии космологическая постоянная). В 1927 г. Жорж Лемэтр показал, что статические решения уравнений Эйнштейна, которые возможны при наличии космологической постоянной, нестабильны, и поэтому статическая Вселенная, представленная Эйнштейном, не может существовать. Позже, в 1931 году, сам Эйнштейн согласился с результатами Фридмана и Леметра. Таким образом, общая теория относительности предсказывала, что Вселенная должна быть нестатической - она должна либо расширяться, либо сжиматься. Расширение Вселенной обнаружено Эдвин Хаббл в 1929 г. подтвердил это предсказание.[27]
- Предсказание теории перетаскивание кадра соответствует недавнему Гравитационный зонд B полученные результаты.[28]
- Общая теория относительности предсказывает, что свет должен терять его энергия при путешествии прочь от массивных тел через гравитационное красное смещение. Это было подтверждено на Земле и в Солнечной системе примерно в 1960 году.
Гравитация и квантовая механика
Остается открытым вопрос, можно ли описать мелкомасштабные взаимодействия гравитации с помощью тех же рамок, что и квантовая механика. Общая теория относительности описывает крупномасштабные объемные свойства, тогда как квантовая механика представляет собой основу для описания взаимодействий материи на самом мелкомасштабном уровне. Без модификаций эти фреймворки несовместимы.[29]
Один из путей - описать гравитацию в рамках квантовая теория поля, который смог точно описать другой фундаментальные взаимодействия. Электромагнитная сила возникает в результате обмена виртуальными фотоны, где КТП описывает гравитацию как обмен виртуальный гравитоны.[30][31] Это описание воспроизводит общую теорию относительности в классический предел. Однако этот подход не работает на малых расстояниях порядка Планковская длина,[29] где более полная теория квантовая гравитация (или новый подход к квантовой механике).
Особенности
Земное притяжение
Каждое планетное тело (включая Землю) окружено своим собственным гравитационным полем, которое можно концептуализировать с помощью ньютоновской физики как приложение силы притяжения ко всем объектам. Если предположить, что планета является сферически-симметричной, сила этого поля в любой заданной точке над поверхностью пропорциональна массе планетарного тела и обратно пропорциональна квадрату расстояния от центра тела.
Сила гравитационного поля численно равна ускорению объектов под его воздействием.[32] Скорость ускорения падающих объектов у поверхности Земли очень незначительно меняется в зависимости от широты, особенностей поверхности, таких как горы и хребты, и, возможно, необычно высокой или низкой подповерхностной плотности.[33] Для мер и весов стандартная сила тяжести значение определяется Международное бюро мер и весов, под Международная система единиц (SI).
Это значение, обозначенное грамм, является грамм = 9.80665 м / с2 (32,1740 фут / с2).[34][35]
Стандартное значение 9,80665 м / с.2 - это тот, который был первоначально принят Международным комитетом по мерам и весам в 1901 году для 45 ° широты, хотя было показано, что он слишком высок примерно на пять частей из десяти тысяч.[36] Это значение сохранилось в метеорологии и в некоторых стандартных атмосферных условиях как значение для широты 45 °, хотя более точно оно применяется к широте 45 ° 32'33 ".[37]
Если принять стандартизованное значение для g и игнорировать сопротивление воздуха, это означает, что объект, свободно падающий возле поверхности Земли, увеличивает свою скорость на 9,80665 м / с (32,1740 футов / с или 22 мили в час) за каждую секунду своего спуска. Таким образом, объект, стартовавший из состояния покоя, достигнет скорости 9,80665 м / с (32,1740 футов / с) через одну секунду, примерно 19,62 м / с (64,4 фута / с) через две секунды и так далее, добавив 9,80665 м / с. (32,1740 фут / с) к каждой результирующей скорости. Кроме того, снова игнорируя сопротивление воздуха, все объекты, падающие с одинаковой высоты, одновременно ударяются о землю.
В соответствии с 3-й закон Ньютона, сама Земля испытывает сила равной по величине и противоположной по направлению тому, что она оказывает на падающий объект. Это означает, что Земля также ускоряется к объекту, пока он не столкнется. Однако, поскольку масса Земли огромна, ускорение, сообщаемое Земле этой противоположной силой, незначительно по сравнению с ускорением объекта. Если объект не отскакивает после столкновения с Землей, каждый из них проявляет отталкивающую силу. контактная сила с другой стороны, эффективно уравновешивает силу притяжения силы тяжести и предотвращает дальнейшее ускорение.
Сила тяжести на Земле является равнодействующей (векторной суммой) двух сил:[38] (а) гравитационное притяжение в соответствии с универсальным законом всемирного тяготения Ньютона и (б) центробежная сила, которая возникает в результате выбора привязанной к Земле вращающейся системы отсчета. Сила тяжести наиболее слабая на экваторе из-за центробежная сила вызвано вращением Земли и тем, что точки на экваторе наиболее удалены от центра Земли. Сила тяжести меняется с широтой и увеличивается примерно от 9,780 м / с.2 на экваторе примерно до 9,832 м / с2 на полюсах.
Уравнения падающего тела у поверхности Земли
В предположении постоянного гравитационного притяжения Закон всемирного тяготения Ньютона упрощает до F = мг, куда м это масса тела и грамм постоянный вектор со средней величиной 9,81 м / с2 на земле. Эта результирующая сила и есть вес объекта. Ускорение свободного падения равно этому грамм. Первоначально неподвижный объект, которому позволено свободно падать под действием силы тяжести, опускается на расстояние, пропорциональное квадрату прошедшего времени. Изображение справа, охватывающее полсекунды, было получено с помощью стробоскопической вспышки с частотой 20 вспышек в секунду. Во время первого1⁄20 за секунду мяч падает на одну единицу расстояния (здесь единица составляет около 12 мм); по2⁄20 упало всего на 4 единицы; по3⁄20, 9 единиц и так далее.
При тех же предположениях о постоянной гравитации потенциальная энергия, Eп, тела на высоте час дан кем-то Eп = mgh (или же Eп = Wh, с W имеется в виду вес). Это выражение справедливо только на малых расстояниях час с поверхности Земли. Аналогично выражение для максимальной высоты, достигаемой вертикально спроецированным телом с начальной скоростью v полезен только для малых высот и малых начальных скоростей.
Гравитация и астрономия
Применение закона всемирного тяготения Ньютона позволило получить большую часть подробной информации, которая у нас есть о планетах в Солнечной системе, массе Солнца и деталях квазары; даже наличие темная материя выводится с использованием закона всемирного тяготения Ньютона.Хотя мы не побывали ни на всех планетах, ни на Солнце, мы знаем их массы. Эти массы получены путем применения законов гравитации к измеренным характеристикам орбиты. В космосе объект сохраняет свое орбита из-за действующей на него силы тяжести. Звезды орбиты планет, орбиты звезд галактические центры, галактики вращаются вокруг центра масс в скоплениях, а скопления вращаются вокруг сверхскопления. Сила тяжести, действующая на один объект со стороны другого, прямо пропорциональна произведению масс этих объектов и обратно пропорциональна квадрату расстояния между ними.
Самая ранняя гравитация (возможно, в форме квантовой гравитации, супергравитация или гравитационная сингулярность), наряду с обычным пространством и временем, развившимися в Эпоха Планка (до 10−43 секунд после рождение Вселенной), возможно, из первобытного состояния (например, ложный вакуум, квантовый вакуум или же виртуальная частица) неизвестным в настоящее время способом.[5]
Гравитационное излучение

Общая теория относительности предсказывает, что энергия может переноситься из системы посредством гравитационного излучения. Любая ускоряющаяся материя может создавать искривления в метрике пространства-времени, благодаря чему гравитационное излучение переносится от системы. Совместно вращающиеся объекты могут создавать искривления в пространстве-времени, такие как система Земля-Солнце, пары нейтронных звезд и пары черных дыр. Другая астрофизическая система, согласно предсказаниям которой теряет энергию в виде гравитационного излучения, - взрывающиеся сверхновые.
Первым косвенным свидетельством гравитационного излучения были измерения Бинарная система Халса – Тейлора в 1973 году. Эта система состоит из пульсара и нейтронной звезды, вращающихся вокруг друг друга. Его орбитальный период уменьшился с момента его первоначального открытия из-за потери энергии, которая соответствует количеству потерь энергии из-за гравитационного излучения. Это исследование было удостоено Нобелевской премии по физике в 1993 году.
Первое прямое свидетельство гравитационного излучения было получено 14 сентября 2015 г. LIGO детекторы. Были измерены гравитационные волны, испускаемые во время столкновения двух черных дыр на расстоянии 1,3 миллиарда световых лет от Земли.[40][41] Это наблюдение подтверждает теоретические предсказания Эйнштейна и других авторов о существовании таких волн. Это также открывает путь для практических наблюдений и понимания природы гравитации и событий во Вселенной, включая Большой взрыв.[42] Нейтронная звезда и черная дыра образования также создают заметное количество гравитационного излучения.[43] Это исследование было удостоено Нобелевской премии по физике в 2017 году.[44]
По состоянию на 2020 год[Обновить], гравитационное излучение, испускаемое Солнечная система слишком мал, чтобы его можно было измерить с помощью современных технологий.
Скорость гравитации
В декабре 2012 года исследовательская группа в Китае объявила, что она произвела измерения фазовой задержки Земные приливы во время полнолуния и новолуния, которые, кажется, доказывают, что скорость гравитации равна скорости света.[45] Это означает, что если Солнце внезапно исчезнет, Земля будет продолжать вращаться вокруг него в обычном режиме в течение 8 минут, а это время, которое требуется свету, чтобы пройти это расстояние. Выводы команды были опубликованы в Китайский научный бюллетень в феврале 2013 г.[46]
В октябре 2017 г. LIGO и детекторы Virgo получали сигналы гравитационных волн в течение 2 секунд, когда спутники гамма-излучения и оптические телескопы видели сигналы с того же направления. Это подтвердило, что скорость гравитационных волн была такой же, как скорость света.[47]
Аномалии и неточности
Есть некоторые наблюдения, которые не учитываются должным образом, что может указывать на необходимость в более совершенных теориях гравитации или, возможно, быть объяснено другими способами.

- Сверхбыстрые звезды: Звезды в галактиках следуют за распределение скоростей где звезды на окраинах движутся быстрее, чем следовало бы в соответствии с наблюдаемыми распределениями нормальной материи. Галактики внутри скопления галактик покажите похожий узор. Темная материя, которые будут взаимодействовать через гравитацию, но не электромагнитно, объяснили бы расхождение. Разные модификации ньютоновской динамики также были предложены.
- Аномалия облета: Различные космические корабли испытали большее ускорение, чем ожидалось помощь гравитации маневры.
- Ускоряющееся расширение: The метрическое расширение пространства похоже, ускоряется. Темная энергия было предложено объяснить это. Недавнее альтернативное объяснение состоит в том, что геометрия пространства неоднородна (из-за скоплений галактик) и что, когда данные интерпретируются заново, чтобы учесть это, расширение в конце концов не ускоряется,[48] однако этот вывод оспаривается.[49]
- Аномальное увеличение астрономическая единица: Последние измерения показывают, что планетные орбиты расширяются быстрее, чем если бы это происходило исключительно из-за потери массы Солнцем за счет излучения энергии.
- Фотоны сверхвысокой энергии: Фотоны, путешествующие через скопления галактик, должны набирать энергию, а затем снова терять ее на выходе. Ускоряющееся расширение Вселенной должно остановить возвращение фотонов всей энергии, но даже с учетом этого космическое микроволновое фоновое излучение получить вдвое больше энергии, чем ожидалось. Это может указывать на то, что гравитация спадает быстрее, чем в обратном квадрате на определенных масштабах расстояний.[50]
- Сверхмассивные водородные облака: Спектральные линии Лиман-альфа лес предполагают, что водородные облака более сгруппированы в определенных масштабах, чем ожидалось, и, например, темный поток, может указывать на то, что гравитация спадает медленнее, чем обратный квадрат на определенных масштабах расстояний.[50]
Альтернативные теории
Исторические альтернативные теории
- Аристотелевская теория гравитации
- Теория гравитации Ле Сажа (1784), также называемый гравитацией Лесажа, предложенный Жорж-Луи Ле Саж, основанный на объяснении, основанном на жидкости, где легкий газ заполняет всю Вселенную.
- Теория гравитации Ритца, Анна. Chem. Phys. 13, 145, (1908) pp. 267–271, Электродинамика Вебера-Гаусса в применении к гравитации. Классическое продвижение перигелии.
- Теория гравитации Нордстрёма (1912, 1913), один из первых конкурентов общей теории относительности.
- Теория Калуцы Клейна (1921)
- Теория гравитации Уайтхеда (1922), еще один ранний конкурент общей теории относительности.
Современные альтернативные теории
- Теория Бранса – Дике гравитации (1961)[51]
- Индуцированная гравитация (1967), предложение Андрей Сахаров в соответствии с которым общая теория относительности может возникнуть из квантовые теории поля материи
- Теория струн (конец 1960-х)
- ƒ (R) гравитация (1970)
- Теория Хорндески (1974)[52]
- Супергравитация (1976)
- в модифицированная ньютоновская динамика (MOND) (1981), Мордехай Милгром предлагает модификацию Второй закон Ньютона движения для малых ускорений[53]
- В космология самотворения теория гравитации (1982) Г.А. Барбер, в котором теория Бранса-Дике модифицирована, чтобы позволить массовое производство
- Петлевая квантовая гравитация (1988) автор Карло Ровелли, Ли Смолин, и Абхай Аштекар
- Несимметричная теория гравитации (NGT) (1994) автор: Джон Моффат
- Тензорно-векторно-скалярная гравитация (TeVeS) (2004), релятивистская модификация MOND, созданная Якоб Бекенштейн
- Теория хамелеона (2004) автор: Джастин Хури и Аманда Велтман.
- Теория прессурона (2013) автор: Оливье Минаццоли и Орелиен Хис.
- Конформная гравитация[54]
- Гравитация как энтропийная сила, гравитация, возникающая как явление, возникающее из термодинамической концепции энтропии.
- в теория сверхтекучего вакуума гравитация и искривленное пространство-время возникают как коллективное возбуждение режим нерелятивистского фона сверхтекучий.
Смотрите также
- Антигравитационный, идея нейтрализации или отражения гравитации
- Искусственная гравитация
- Закон Гаусса для гравитации
- Гравитационный потенциал
- Гравитационная волна
- Третий закон движения планет Кеплера
- Микро-среда, также называемый микрогравитацией
- Законы движения Ньютона
- Стандартный гравитационный параметр
- Невесомость
Сноски
- ^ dict.cc словарь :: gravitas :: английский-латинский перевод
- ^ Коминс, Нил Ф .; Кауфманн, Уильям Дж. (2008). Открытие Вселенной: от звезд до планет. Макмиллан. п. 347. Bibcode:2009dufs.book ..... C. ISBN 978-1429230421.
- ^ "ХабблСайт: Черные дыры: неумолимое притяжение гравитации". hubblesite.org. Получено 7 октября 2016.
- ^ Кребс, Роберт Э. (1999). Научное развитие и заблуждения сквозь века: справочное руководство (иллюстрированный ред.). Издательская группа "Гринвуд". п.133. ISBN 978-0-313-30226-8.
- ^ а б Сотрудники. «Рождение Вселенной». Орегонский университет. Получено 24 сентября 2016. - обсуждает »Планковское время" и "Планковская эпоха"на самое начало Вселенной
- ^ Ревиль Нейтц; Уильям Ноэль (13 октября 2011 г.). Кодекс Архимеда: раскрытие секретов величайшего в мире палимпсеста. Hachette UK. п. 125. ISBN 978-1-78022-198-4.CS1 maint: несколько имен: список авторов (связь)
- ^ CJ Tuplin, Льюис Вулперт (2002). Наука и математика в древнегреческой культуре. Hachette UK. п. xi. ISBN 978-0-19-815248-4.
- ^ Витрувий, Марк Поллион (1914). "7". В Альфред А. Ховард (ред.). De Architectura libri decem [Десять книг по архитектуре]. VII. Герберт Лэнгфорд Уоррен, Нельсон Робинсон (иллюстрация), Моррис Хики Морган. Гарвардский университет, Кембридж: Издательство Гарвардского университета. п. 215.
- ^ Пиковер, Клиффорд (16 апреля 2008 г.). От Архимеда до Хокинга: законы науки и великие умы, стоящие за ними. Издательство Оксфордского университета. ISBN 9780199792689.
- ^ *Сен, Амартия (2005). Аргументативный индеец. Аллен Лейн. п. 29. ISBN 978-0-7139-9687-6.
- ^ Болл, Фил (июнь 2005 г.). «Сказки». Новости природы. Дои:10.1038 / news050613-10.
- ^ Галилео (1638), Две новые науки, Первый день Сальвиати говорит: «Если бы это имел в виду Аристотель, вы бы обременяли его еще одной ошибкой, которая была бы равносильна лжи; поскольку, поскольку на Земле нет такой абсолютной высоты, ясно, что Аристотель не мог бы сделать это. эксперимент; тем не менее, он хочет создать у нас впечатление, что он выполнил его, когда он говорит о таком эффекте, как тот, который мы видим ».
- ^ Бонгаартс, Питер (2014). Квантовая теория: математический подход (иллюстрированный ред.). Springer. п. 11. ISBN 978-3-319-09561-5.
- ^ *Чандрасекар, Субраманян (2003). Начала Ньютона для обычного читателя. Оксфорд: Издательство Оксфордского университета. (стр. 1–2). Цитата взята из меморандума, который, как считается, был написан около 1714 года. Еще в 1645 году. Исмаэль Буллиальдус утверждал, что любая сила, действующая со стороны Солнца на далекие объекты, должна подчиняться закону обратных квадратов. Однако он также отверг идею о существовании такой силы. См., Например,Линтон, Кристофер М. (2004). От Евдокса до Эйнштейна - история математической астрономии. Кембридж: Издательство Кембриджского университета. п.225. ISBN 978-0-521-82750-8.
- ^ Нобиль, Анна М. (март 1986 г.). «Реальная стоимость продвижения перигелия Меркурия». Природа. 320 (6057): 39–41. Bibcode:1986Натура.320 ... 39Н. Дои:10.1038 / 320039a0. S2CID 4325839.
- ^ М. В. Сэндфорд (2008). «ШАГ: спутниковая проверка принципа эквивалентности». Лаборатория Резерфорда Эпплтона. Архивировано из оригинал 28 сентября 2011 г.. Получено 14 октября 2011.
- ^ Пол С. Вессон (2006). Пятимерная физика. World Scientific. п.82. ISBN 978-981-256-661-4.
- ^ Haugen, Mark P .; К. Леммерцаль (2001), «Принципы эквивалентности: их роль в физике гравитации и эксперименты, которые их проверяют», Гироскопы, Конспект лекций по физике, 562 (562, Гироскопы, часы и интерферометры ...: Проверка релятивистской гравитации в космосе): 195–212, arXiv:gr-qc / 0103067, Bibcode:2001ЛНП ... 562..195Н, Дои:10.1007/3-540-40988-2_10, S2CID 15430387
- ^ «Гравитация и искривленное пространство-время». black-holes.org. Архивировано из оригинал 21 июня 2011 г.. Получено 16 октября 2010.
- ^ Дмитрий Погосян. «Лекция 20: Черные дыры - принцип эквивалентности Эйнштейна». Университет Альберты. Получено 14 октября 2011.
- ^ Паули, Вольфганг Эрнст (1958). «Часть IV. Общая теория относительности». Теория относительности. Courier Dover Publications. ISBN 978-0-486-64152-2.
- ^ Макс Борн (1924), Теория относительности Эйнштейна (В издании Dover 1962 года, стр. 348 приведена таблица, в которой задокументированы наблюдаемые и рассчитанные значения прецессии перигелия Меркурия, Венеры и Земли.)
- ^ Дайсон, Ф.; Эддингтон, А.; Дэвидсон, C.R. (1920). "Определение отклонения света гравитационным полем Солнца по наблюдениям, сделанным во время полного затмения 29 мая 1919 г.". Фил. Пер. Рой. Soc. А. 220 (571–581): 291–333. Bibcode:1920RSPTA.220..291D. Дои:10.1098 / рста.1920.0009.. Цитата, стр. 332: «Таким образом, результаты экспедиций в Собрал и Принсипи не могут оставлять никаких сомнений в том, что отклонение света происходит поблизости от Солнца и что оно соответствует величине, требуемой обобщенной теорией относительности Эйнштейна, как относительности Солнца. гравитационное поле ".
- ^ Вайнберг, Стивен (1972). Гравитация и космология. Джон Вили и сыновья.. Цитата, стр. 192: «Всего было изучено около дюжины звезд, и были получены значения 1,98 ± 0,11» и 1,61 ± 0,31 », что в значительной степени согласуется с предсказанием Эйнштейна θ☉ = 1.75"."
- ^ Эрман, Джон; Глимур, Кларк (1980). «Относительность и затмения: Британские экспедиции по затмениям 1919 года и их предшественники». Исторические исследования в физических науках. 11 (1): 49–85. Дои:10.2307/27757471. JSTOR 27757471. S2CID 117096916.
- ^ Вайнберг, Стивен (1972). Гравитация и космология. Джон Вили и сыновья. п.194.
- ^ См. W.Pauli, 1958, pp. 219–220.
- ^ «Гравитационный зонд B НАСА подтверждает две теории пространства-времени Эйнштейна». Nasa.gov. Получено 23 июля 2013.
- ^ а б Рэндалл, Лиза (2005). Искаженные проходы: открытие скрытых измерений Вселенной. Ecco. ISBN 978-0-06-053108-9.
- ^ Feynman, R.P .; Morinigo, F.B .; Wagner, W.G .; Хэтфилд, Б. (1995). Лекции Фейнмана о гравитации. Эддисон-Уэсли. ISBN 978-0-201-62734-3.
- ^ Зи, А. (2003). Квантовая теория поля в двух словах. Издательство Принстонского университета. ISBN 978-0-691-01019-9.
- ^ Cantor, G.N .; Christie, J.R.R .; Ходж, M.J.S .; Олби, Р. (2006). Товарищ по истории современной науки. Рутледж. п. 448. ISBN 978-1-134-97751-2.
- ^ Nemiroff, R .; Боннелл, Дж., Ред. (15 декабря 2014 г.). "Потсдамский гравитационный картофель". Астрономическая картина дня. НАСА.
- ^ Международное бюро поид и мер (2006 г.). «Международная система единиц (СИ)» (PDF) (8-е изд.): 131.
Названия единиц обычно печатаются римским (прямым) шрифтом ... Символы для количеств обычно представляют собой отдельные буквы, набранные курсивом, хотя они могут быть дополнены дополнительной информацией в нижних или верхних индексах или в скобках.
Цитировать журнал требует| журнал =(помощь) - ^ «Правила единиц СИ и стилистические соглашения». Национальный институт стандартов и технологий (США). Сентябрь 2004 г.
Переменные и символы количества выделены курсивом. Обозначения единиц выполнены римским шрифтом.
- ^ Лист, Р.Дж. редактор, 1968, Acceleration of Gravity, Смитсоновские метеорологические таблицы, Шестое изд. Смитсоновский институт, Вашингтон, округ Колумбия, стр. 68.
- ^ Стандартная атмосфера США, 1976, Типография правительства США, Вашингтон, округ Колумбия, 1976 г. (Связанный файл очень большой.)
- ^ Hofmann-Wellenhof, B .; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Springer. ISBN 978-3-211-33544-4. § 2.1: «Полная сила, действующая на тело, покоящееся на поверхности земли, является равнодействующей гравитационной силы и центробежной силы вращения Земли и называется гравитацией».
- ^ "Млечный Путь появляется, когда солнце садится над Параналом". www.eso.org. Европейская южная обсеватория. Получено 29 апреля 2015.
- ^ Кларк, Стюарт (11 февраля 2016 г.). «Гравитационные волны: ученые объявляют:« Мы сделали это! » - жить". хранитель. Получено 11 февраля 2016.
- ^ Кастельвекки, Давиде; Витце, Витце (11 февраля 2016 г.). «Наконец-то найдены гравитационные волны Эйнштейна». Новости природы. Дои:10.1038 / природа.2016.19361. S2CID 182916902. Получено 11 февраля 2016.
- ^ «ЧТО ТАКОЕ ГРАВИТАЦИОННЫЕ ВОЛНЫ И ПОЧЕМУ ОНИ ВАЖНЫ?». popsci.com. Получено 12 февраля 2016.
- ^ Abbott, B.P .; и другие. (LIGO Scientific Collaboration & Дева Сотрудничество) (Октябрь 2017 г.). "GW170817: Наблюдение гравитационных волн от двойной нейтронной звезды в спирали" (PDF). Письма с физическими проверками. 119 (16): 161101. arXiv:1710.05832. Bibcode:2017ПхРвЛ.119п1101А. Дои:10.1103 / PhysRevLett.119.161101. PMID 29099225.
- ^ Девлин, Ханна (3 октября 2017 г.). «Нобелевская премия по физике за открытие гравитационных волн». хранитель. Получено 3 октября 2017.
- ^ Китайские ученые нашли доказательства скорости гравитации, astrowatch.com, 28 декабря 2012 г.
- ^ ТАН, Кэ Юн; HUA ChangCai; ВЕН Ву; CHI ShunLiang; ВЫ QingYu; Ю Дан (февраль 2013 г.). «Наблюдательные доказательства скорости гравитации на основе земного прилива». Китайский научный бюллетень. 58 (4–5): 474–477. Bibcode:2013ЧСБУ..58..474Т. Дои:10.1007 / s11434-012-5603-3.
- ^ "GW170817 Пресс-релиз". LIGO Lab - Калифорнийский технологический институт.
- ^ Темная энергия может быть просто космической иллюзией, Новый ученый, выпуск 2646, 7 марта 2008 г.
- ^ Дырявая модель космоса из швейцарского сыра, Новый ученый, выпуск 2678, 18 октября 2008 г.
- ^ а б Чоун, Маркус (16 марта 2009 г.). «Гравитация может отважиться туда, куда материя боится ступить». Новый ученый. Получено 4 августа 2013.
- ^ Бранс, Ч. (Март 2014 г.). "Теория Джордана-Бранса-Дике". Scholarpedia. 9 (4): 31358. arXiv:gr-qc / 0207039. Bibcode:2014Schpj ... 931358B. Дои:10.4249 / scholarpedia.31358.
- ^ Хорндески, Г. (Сентябрь 1974 г.). "Уравнения скалярно-тензорного поля второго порядка в четырехмерном пространстве". Международный журнал теоретической физики. 88 (10): 363–384. Bibcode:1974IJTP ... 10..363H. Дои:10.1007 / BF01807638. S2CID 122346086.
- ^ Милгром, М. (июнь 2014 г.). «Парадигма модифицированной динамики MOND». Scholarpedia. 9 (6): 31410. Bibcode:2014SchpJ ... 931410M. Дои:10.4249 / scholarpedia.31410.
- ^ Haugan, Mark P; Леммерцаль, С. (2011). «Гравитация Эйнштейна из конформной гравитации». arXiv:1105.5632 [hep-th].
Рекомендации
- Холлидей, Дэвид; Роберт Резник; Кеннет С. Крейн (2001). Физика v. 1. Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-32057-9.
- Serway, Raymond A .; Джуэтт, Джон В. (2004). Физика для ученых и инженеров (6-е изд.). Брукс / Коул. ISBN 978-0-534-40842-8.
- Типлер, Пол (2004). Физика для ученых и инженеров: механика, колебания и волны, термодинамика (5-е изд.). W.H. Фримен. ISBN 978-0-7167-0809-4.
дальнейшее чтение
- Торн, Кип С.; Миснер, Чарльз У .; Уилер, Джон Арчибальд (1973). Гравитация. W.H. Фримен. ISBN 978-0-7167-0344-0.
- Панек, Ричард (2 августа 2019 г.). "Все, что вы думали, что знаете о гравитации, неверно". Вашингтон Пост.
внешняя ссылка
- «Гравитация», Энциклопедия математики, EMS Press, 2001 [1994]
- "Гравитация, теория", Энциклопедия математики, EMS Press, 2001 [1994]







