WikiDer > Гравитационная сингулярность

Анимированное моделирование гравитационное линзирование вызвано Черная дыра Шварцшильда переходящий в прямой видимости планарную к фоновой галактике. Примерно и во время точного совмещения (сизигия) наблюдается крайнее линзирование света.

Часть цикла статей о
Общая теория относительности
${ displaystyle G _ { mu nu} + Lambda g _ { mu nu} = { frac {8 pi G} {c ^ {4}}} T _ { mu nu}}$
Введение История Математическая формулировка Тесты
Основные концепции Принцип относительности Теория относительности Точка зрения Инерциальная система отсчета Рама отдыха Рамка центра импульса Световой конус Принцип эквивалентности Эквивалентность массы и энергии Специальная теория относительности Двойная специальная теория относительности инвариант де Ситтера специальная теория относительности Масштаб относительности Мировая линия Подходящее время Риманова геометрия Энергетическое состояние
Явления Гравитоэлектромагнетизм Проблема Кеплера Сила тяжести Гравитационное поле Гравитационный колодец Гравитационное линзирование Гравитационные волны Гравитационное красное смещение Красное смещение Синий сдвиг Замедление времени Гравитационное замедление времени Задержка Шапиро Гравитационный потенциал Гравитационное сжатие Гравитационный коллапс Перетаскивание кадра Геодезический эффект Видимый горизонт Горизонт событий Гравитационная сингулярность Обнаженная особенность Черная дыра Белая дыра Пространство-время Космос Время Диаграммы пространства-времени Пространство-время Минковского Замкнутая времениподобная кривая (СТС) Червоточина Червоточина Эллиса
Уравнения Формализмы Уравнения Линеаризованная гравитация Уравнения поля Эйнштейна Фридман Геодезические Матиссон – Папапетру – Диксон Гамильтон – Якоби – Эйнштейн Инвариант кривизны (общая теория относительности) Лоренцево многообразие Формализмы ADM БССН Ньюман – Пенроуз Постньютоновский Продвинутая теория Теория Калуцы – Клейна Квантовая гравитация Супергравитация
Решения Шварцшильд (интерьер) Рейсснер-Нордстрём Гёдель Керр Керр – Ньюман Kasner Лемэтр – Толман Тауб-ОРЕХ Milne Робертсон – Уокер pp-волна van Stockum пыль Вейль – Льюис – Папапетру Вакуумный раствор
Теоремы Теорема Биркгофа Теорема Героха о расщеплении Теорема Гольдберга – Сакса. Теорема Лавлока Теорема об отсутствии волос Теоремы Пенроуза – Хокинга об особенностях Теорема положительной энергии
Ученые Эйнштейн Лоренц Гильберта Пуанкаре Шварцшильд де Ситтер Рейсснер Nordström Weyl Эддингтон Фридман Milne Цвикки Лемэтр Гёдель Уиллер Робертсон Бардин Уокер Керр Чандрасекхар Элерс Пенроуз Хокинг Райчаудхури Тейлор Hulse van Stockum Тауб Новый человек Яу Торн другие
v т е

А гравитационная сингулярность, сингулярность пространства-времени или просто необычность это место в пространство-время где масса и гравитационное поле предсказывается, что небесное тело станет бесконечный от общая теория относительности способом, который не зависит от система координат. Величины, используемые для измерения напряженности гравитационного поля: скалярный инвариант искривления пространства-времени, которое включает меру плотности материи. Поскольку в сингулярности такие величины становятся бесконечными, законы нормального пространства-времени нарушаются.^[1][2]

Гравитационные особенности рассматриваются в основном в контексте общая теория относительности, где плотность очевидно становится бесконечным в центре черная дыра, а внутри астрофизика и космология как самое раннее состояние вселенной в течение Большой взрыв. Физики не уверены, означает ли предсказание сингулярностей, что они действительно существуют (или существовали в начале Большого взрыва), или что текущих знаний недостаточно для описания того, что происходит при таких экстремальных плотностях.

Общая теория относительности предсказывает, что любой объект коллапсирует за пределами определенной точки (для звезды это Радиус Шварцшильда) образовала бы черную дыру, внутри которой образовалась бы сингулярность (покрытая горизонтом событий).^[3] В Теоремы Пенроуза – Хокинга об особенностях определить сингулярность, чтобы иметь геодезические что не может быть продлено в гладкий; плавный манера.^[4] Окончание такой геодезической считается особенностью.

Исходное состояние вселенная, в начале Большой взрыв, также предсказывается современными теориями как сингулярность.^[5] В этом случае Вселенная не коллапсировала в черную дыру, потому что известные в настоящее время расчеты и пределы плотности для гравитационного коллапса обычно основаны на объектах относительно постоянного размера, таких как звезды, и не обязательно применяются таким же образом к быстро расширяющееся пространство такие как Большой взрыв. Ни то, ни другое общая теория относительности ни квантовая механика в настоящее время могу описать самые ранние моменты Большого взрыва,^[6] но в целом квантовая механика не позволяет частицам населять пространство меньше их длины волн.^[7]

Интерпретация

Многие теории в физике математические особенности того или иного вида. Уравнения для этих физических теорий предсказывают, что шар массы некоторой величины становится бесконечным или неограниченно увеличивается. Как правило, это признак того, что в теории что-то не так. ультрафиолетовая катастрофа, повторная нормализация, и нестабильность атома водорода, предсказываемая Формула лармора.

Некоторые теории, такие как теория петля квантовой гравитации, предполагают, что особенности могут не существовать.^[8] Это также верно для таких классических теорий единого поля, как Уравнения Эйнштейна – Максвелла – Дирака.. Идею можно изложить в том виде, в котором благодаря квантовая гравитация эффекты, существует минимальное расстояние, за которым сила тяжести больше не продолжает увеличиваться, поскольку расстояние между массами становится короче, или, альтернативно, взаимопроникающие волны частиц маскируют гравитационные эффекты, которые могут ощущаться на расстоянии.

Типы

Существуют разные типы сингулярностей, каждая из которых имеет разные физические особенности, которые имеют характеристики, относящиеся к теориям, из которых они изначально возникли, такие как различная форма сингулярностей, конический и изогнутый. Также была выдвинута гипотеза, что они происходят без горизонтов событий, структур, которые отделяют один участок пространства-времени от другого, в котором события не могут повлиять за пределы горизонта; они называются голый.

Коническая

Коническая особенность возникает, когда существует точка, в которой предел каждого инвариант диффеоморфизма количество конечно, и в этом случае пространство-время не является гладким в самой точке предела. Таким образом, пространство-время выглядит как конус вокруг этой точки, где сингулярность расположена на вершине конуса. Метрика может быть конечной всюду система координат используется.

Примером такой конической особенности является космическая струна и Черная дыра Шварцшильда.^[9]

Кривизна

Простая иллюстрация не вращающегося черная дыра и его особенность

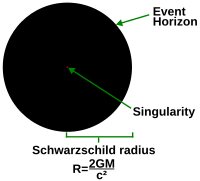
Решения уравнений общая теория относительности или другая теория сила тяжести (такие как супергравитация) часто приводят к обнаружению точек, где метрика взрывается до бесконечности. Однако многие из этих моментов полностью регулярный, а бесконечности - просто результат используя неподходящую систему координат в этот момент. Чтобы проверить, есть ли особенность в определенной точке, нужно проверить, есть ли в этой точке инвариант диффеоморфизма количества (т.е. скаляры) становятся бесконечными. Такие величины одинаковы во всех системах координат, поэтому эти бесконечности не «уйдут» из-за смены координат.

Примером может служить Шварцшильд решение, описывающее невращающуюся, незаряженный черная дыра. В системах координат, удобных для работы в областях, далеких от черной дыры, часть метрики становится бесконечной в точке горизонт событий. Однако пространство-время на горизонте событий равно регулярный. Регулярность становится очевидной при переходе к другой системе координат (такой как Крускал координаты), где метрика идеально гладкий; плавный. С другой стороны, в центре черной дыры, где метрика также становится бесконечной, решения предполагают наличие сингулярности. Существование особенности можно проверить, отметив, что Скаляр Кречмана, являясь квадратом Тензор Римана т.е. ${ Displaystyle Р _ { му ню ро сигма} Р ^ { му ню ро сигма}}$, инвариантный к диффеоморфизму, бесконечен.

В то время как в невращающейся черной дыре сингулярность возникает в единственной точке в координатах модели, называемой «точечной сингулярностью», во вращающейся черной дыре, также известной как Черная дыра Керра, особенность возникает на кольце (круговой линии), известном как "кольцевая особенность". Такая особенность теоретически может также стать червоточина.^[10]

В более общем смысле пространство-время считается единичным, если оно геодезически неполный, что означает, что существуют свободно падающие частицы, движение которых невозможно определить за конечное время, находящееся после точки достижения сингулярности. Например, любой наблюдатель внутри горизонт событий невращающейся черной дыры упадет в ее центр за конечный период времени. Классический вариант Большой взрыв космологический модель вселенная содержит причинную особенность в начале время (т= 0), где все временные геодезические не имеют продолжения в прошлом. Экстраполяция назад к этому гипотетическому времени 0 приводит к Вселенной со всеми пространственными измерениями нулевого размера, бесконечной плотности, бесконечной температуры и бесконечной кривизны пространства-времени.

Обнаженная особенность

До начала 1990-х было широко распространено мнение, что общая теория относительности скрывает каждую особенность за горизонт событий, что делает невозможными голые особенности. Это называется гипотеза космической цензуры. Однако в 1991 году физики Стюарт Шапиро и Саул Теукольский провели компьютерное моделирование вращающейся плоскости пыли, которое показало, что общая теория относительности может допускать «голые» сингулярности. Как на самом деле будут выглядеть эти объекты в такой модели, неизвестно. Также неизвестно, возникли бы сингулярности по-прежнему, если бы упрощающие допущения, использованные при моделировании, были удалены. Однако существует гипотеза, что свет, попадающий в сингулярность, аналогичным образом теряет геодезические, что делает голая особенность похожи на черную дыру.^[11][12][13]

Исчезающие горизонты событий существуют вМетрика Керра, которая является вращающейся черной дырой в вакууме, еслиугловой момент (${ displaystyle J}$) достаточно высока. Преобразование метрики Керра вКоординаты Бойера – Линдквиста, это можно показать^[14] что координата (которая не является радиусом) горизонта событий, ${ displaystyle r _ { pm} = mu pm ( mu ^ {2} -a ^ {2}) ^ {1/2}}$, где${ displaystyle mu = GM / c ^ {2}}$, и${ displaystyle a = J / Mc}$. В этом случае «горизонты событий исчезают» означает, что решения сложны для${ displaystyle r _ { pm}}$, или${ Displaystyle mu ^ {2} <а ^ {2}}$. Однако это соответствует случаю, когда ${ displaystyle J}$ превышает ${ displaystyle GM ^ {2} / c}$ (или в Планковские единицы, ${ displaystyle J> M ^ {2}}$), то есть спин превышает то, что обычно рассматривается как верхний предел его физически возможных значений.

Точно так же исчезающие горизонты событий также можно увидеть с помощьюРейсснер-Нордстрём геометрия заряженной черной дыры, если заряд (${ displaystyle Q}$) достаточно высока. В этой метрике можно показать^[15] что особенности возникают в ${ displaystyle r _ { pm} = mu pm ( mu ^ {2} -q ^ {2}) ^ {1/2}}$, где${ displaystyle mu = GM / c ^ {2}}$, и${ displaystyle q ^ {2} = GQ ^ {2} / (4 pi epsilon _ {0} c ^ {4})}$. Из трех возможных случаев относительных значений${ displaystyle mu}$ и${ displaystyle q}$, случай, когда${ Displaystyle му ^ {2} <д ^ {2}}$ вызывает оба${ displaystyle r _ { pm}}$ быть сложным. Это означает, что метрика регулярна для всех положительных значений${ displaystyle r}$или, другими словами, сингулярность не имеет горизонта событий. Однако это соответствует случаю, когда ${ displaystyle Q / { sqrt {4 pi epsilon _ {0}}}}$ превышает ${ displaystyle M { sqrt {G}}}$ (или в единицах Планка, ${ displaystyle Q> M}$), т.е. заряд превышает то, что обычно рассматривается как верхний предел его физически возможных значений. Кроме того, не ожидается, что настоящие астрофизические черные дыры будут обладать заметным зарядом.

Черная дыра, обладающая самым низким ${ displaystyle M}$ значение соответствует его ${ displaystyle J}$ и ${ displaystyle Q}$ значения и пределы, указанные выше, т. е. тот, который находится на грани потери горизонта событий, называется экстремальный.

Энтропия

Перед Стивен Хокинг придумал концепцию Радиация Хокинга, вопрос об энтропии черных дыр был решен. Однако эта концепция демонстрирует, что черные дыры излучают энергию, которая сохраняет энтропию и решает проблемы несовместимости с второй закон термодинамики. Энтропия, однако, подразумевает тепло и, следовательно, температуру. Потеря энергии также означает, что черные дыры не существуют вечно, а скорее испаряются или распадаются медленно. Температура черной дыры обратно пропорционально массе.^[16] Все известные кандидаты в черные дыры настолько велики, что их температура намного ниже температуры космического фонового излучения, а это означает, что они будут получать энергию в чистом виде, поглощая это излучение. Они не могут начать терять энергию в сети, пока фоновая температура не упадет ниже их собственной температуры. Это произойдет в космологическое красное смещение более миллиона, а не тысячи или около того с момента образования радиационного фона.^{[нужна цитата]}

Смотрите также

Заметки

использованная литература

• Роджер Пенроуз (1996). «Чандрасекар, черные дыры и сингулярности». ias.ac.in.
• Роджер Пенроуз (1999). «Вопрос о космической цензуре». ias.ac.in.
• Τ. П. Сингх. «Гравитационный коллапс, черные дыры и голые сингулярности». ias.ac.in.

дальнейшее чтение

• Элегантная Вселенная от Брайан Грин. Эта книга дает непрофессионалэто введение в теорию струн, хотя некоторые из высказываемых взглядов уже устарели. Использование общих терминов и приведение примеров по всему тексту помогают непрофессионалам понять основы теории струн.