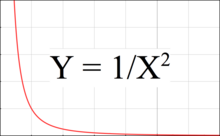WikiDer > Приливная сила

В приливная сила это сила, которая растягивает тело к и от центр массы другого тела из-за градиент (разница в силе) в гравитационное поле от другого тела; он отвечает за различные явления, в том числе приливы, приливная блокировка, разрушение небесных тел и образование кольцевые системы в пределах Предел Роша, а в крайних случаях спагеттификация объектов. Он возникает из-за того, что гравитационное поле, действующее на одно тело другим, непостоянно по всем его частям: ближайшая сторона притягивается сильнее, чем самая дальняя. Именно эта разница заставляет тело растягиваться. Таким образом, приливная сила также известна как дифференциальная сила, а также вторичный эффект гравитационного поля.

В небесная механика, выражение приливная сила может относиться к ситуации, в которой тело или материал (например, приливная вода) находится в основном под гравитационным влиянием второго тела (например, Земли), но также возмущается гравитационными эффектами третьего тела (например, например, Луна). Возмущающую силу в таких случаях иногда называют приливной силой.^[1] (например, возмущающая сила на Луне): это разница между силой, прилагаемой третьим телом ко второму, и силой, прилагаемой третьим телом к ​​первому.^[2]

Объяснение

Рисунок 4: Гравитация Луны дифференциал поле на поверхности Земли известно (наряду с другим, более слабым дифференциальным эффектом, обусловленным Солнцем) как Сила, генерирующая приливы. Это основной механизм, управляющий приливным действием, объясняющий два приливных воздействия. эквипотенциальный выпуклости и два прилива в день. На этом рисунке Земля изображена в центре синего круга, а Луна находится далеко справа. В наружу направление стрелок справа и слева указывает на то, где Луна находится над головой (или надир) его возмущающая сила противоположна силе между землей и океаном.

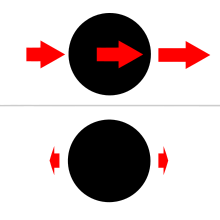
Когда на тело (тело 1) действует сила тяжести другого тела (тела 2), поле может значительно варьироваться на теле 1 между стороной обращенного к телу тела 2 и стороной, обращенной от тела 2. На рисунке 4 показано дифференциальная сила тяжести, действующая на сферическое тело (тело 1) со стороны другого тела (тела 2). Эти так называемые приливные силы вызывают напряжение на обоих телах и могут исказить их или даже, в крайних случаях, сломать одно или другое.^[3] В Предел Роша - это расстояние от планеты, на котором приливные эффекты могут вызвать распад объекта, потому что дифференциальная сила тяжести планеты преодолевает притяжение частей объекта друг к другу.^[4] Эти деформации не возникли бы, если бы гравитационное поле было однородным, потому что однородное поле только заставляет все тело вместе ускоряться в одном направлении и с одинаковой скоростью.

Размер и расстояние

Отношение размера астрономического тела к его расстоянию от другого тела сильно влияет на величину приливной силы.^[5] Приливная сила, действующая на астрономическое тело, такое как Земля, прямо пропорциональна диаметру этого астрономического тела и обратно пропорциональна кубу расстояния от другого тела, создающего гравитационное притяжение, такого как Луна или Солнце. Приливное воздействие на ванны, бассейны, озера и другие небольшие водоемы незначительно.^[6]

Рисунок 3: График, показывающий, как гравитационное притяжение спадает с увеличением расстояния от тела

На рисунке 3 показан график, показывающий, как сила тяжести уменьшается с расстоянием. На этом графике сила притяжения уменьшается пропорционально квадрату расстояния, в то время как наклон относительно значения уменьшается прямо пропорционально расстоянию. Вот почему градиент или приливная сила в любой точке обратно пропорциональны кубу расстояния.

Приливная сила соответствует разнице Y между двумя точками на графике: одна точка находится на ближней стороне тела, а другая - на дальней стороне. Приливная сила увеличивается, когда две точки находятся либо дальше друг от друга, либо когда они располагаются левее на графике, то есть ближе к притягивающему телу.

Например, Луна создает большую приливную силу на Земле, чем Солнце, даже если Солнце оказывает большее гравитационное притяжение на Земле, чем Луна, потому что градиент меньше. Приливная сила пропорциональна массе вызывающего ее тела и радиусу тела, подверженного ей. Земля в 81 раз массивнее Луны, но ее радиус примерно в 4 раза больше. Следовательно, на том же расстоянии Земля создает большую приливную силу на Луне, чем приливная сила Луны на Земле.^[7]

Гравитационное притяжение обратно пропорционально квадрату расстояния от источника. Притяжение будет сильнее на стороне тела, обращенной к источнику, и слабее на стороне, противоположной источнику. Приливная сила пропорциональна разнице.^[6]

Солнце, Земля и Луна

Как и ожидалось, в таблице ниже показано, что расстояние от Луны до Земли такое же, как расстояние от Земли до Луны. Земля в 81 раз массивнее Луны, но ее радиус примерно в 4 раза больше. В результате на том же расстоянии приливная сила Земли на поверхности Луны примерно в 20 раз сильнее, чем приливная сила Луны на поверхности Земли.

Гравитационное тело, вызывающее приливную силу		Тело подвержено приливной силе			Диаметр и расстояние	Приливная сила
Тело	Масса (м)	Тело	Радиус (р)	Расстояние (d)	${displaystyle {frac {2r} {d ^ {3}}}}$	${displaystyle Gm ~ {гидроразрыв {2r} {d ^ {3}}}}$
солнце	1.99×1030 кг	земной шар	6.37×106 м	1.50×1011 м	3.81×10−27 м−2	5.05×10−7 мес−2
Луна	7.34×1022 кг	земной шар	6.37×106 м	3.84×108 м	2.24×10−19 м−2	1.10×10−6 мес−2
земной шар	5.97×1024 кг	Луна	1.74×106 м	3.84×108 м	6.12×10−20 м−2	2.44×10−5 мес−2
м масса; р радиус; d расстояние; 2р это диаметр грамм это гравитационная постоянная = 6.674×10−11 м3⋅кг−1⋅s−2[8]

Последствия

Фигура 5: Сатурнкольца находятся внутри орбит его главных спутников. Приливные силы противодействуют гравитационному слиянию материала в кольцах с образованием лун.^[9]

В случае бесконечно малой упругой сферы действие приливной силы должно исказить форму тела без какого-либо изменения объема. Сфера становится эллипсоид с двумя выпуклостями, направленными к другому телу и от него. Более крупные объекты искажаются яйцевидный, и слегка сжаты, что и происходит с океанами Земли под действием Луны. Земля и Луна вращаются вокруг своего общего центра масс или барицентр, а их гравитационное притяжение обеспечивает центростремительная сила необходимо для поддержания этого движения. Для наблюдателя на Земле, очень близко к этому барицентру, ситуация - это Земля как тело 1, на которое действует гравитация Луны как на тело 2. Все части Земли подвержены гравитационным силам Луны, вызывая вода в океанах перераспределяется, образуя выпуклости по бокам около Луны и вдали от Луны.^[10]

Когда тело вращается под действием приливных сил, внутреннее трение приводит к постепенному рассеиванию его кинетической энергии вращения в виде тепла. В случае Земли и Луны потеря кинетической энергии вращения приводит к увеличению примерно на 2 миллисекунды за столетие. Если тело находится достаточно близко к своему основному, это может привести к вращению, которое приливно заблокирован к орбитальному движению, как в случае с Землей. Приливное отопление производит драматические вулканические эффекты на спутнике Юпитера Ио. Стрессы вызванные приливными силами, также вызывают регулярный ежемесячный график лунотрясения на Луне Земли.^[5]

Приливные силы способствуют возникновению океанских течений, которые смягчают глобальные температуры, передавая тепловую энергию к полюсам. Было высказано предположение, что вариации приливных сил коррелируют с периодами похолодания в записях глобальной температуры с интервалами от 6 до 10 лет,^[11] и это гармонический ритм вариации приливного воздействия могут способствовать изменению климата на протяжении тысячелетий. На сегодняшний день не обнаружено прочной связи с изменениями климата тысячелетия.^[12]

Рисунок 1: Комета Шумейкера-Леви 9 в 1994 году после расставания под влиянием Юпитерприливные силы России во время предыдущего прохода в 1992 году.

Приливные эффекты становятся особенно заметными вблизи небольших тел большой массы, таких как нейтронные звезды или же черные дыры, где они несут ответственность за "спагеттификация"падающей материи. Приливные силы создают океанический прилив из земной шарокеаны, где притягивающими телами являются Луна и, в меньшей степени, солнце. Приливные силы также несут ответственность за приливная блокировка, приливное ускорение, и приливное отопление. Приливы также могут вызывать сейсмичность.

Создавая проводящие жидкости внутри Земли, приливные силы также влияют на Магнитное поле Земли.^[13]

Воспроизвести медиа

Рисунок 2: Это моделирование показывает звезда раздираемый гравитационными приливами огромная черная дыра.

Формулировка

Рисунок 6: Приливная сила ответственна за слияние галактической пары MRK 1034.^[14]

Рисунок 7: График приливных сил. На верхнем рисунке справа показано гравитационное поле тела, на нижнем - их остаток после вычитания поля в центре сферы; это приливная сила. См. Рисунок 4 для более подробной версии.

Для заданного (генерируемого извне) гравитационного поля приливное ускорение в точке относительно тела получается векторное вычитание гравитационного ускорения в центре тела (из-за данного внешне генерируемого поля) от гравитационного ускорения (из-за того же поля) в данной точке. Соответственно срок приливная сила используется для описания сил, вызванных приливным ускорением. Обратите внимание, что для этих целей рассматривается только внешнее гравитационное поле; гравитационное поле тела (как показано на рисунке) не имеет значения. (Другими словами, сравнение проводится с условиями в данной точке, какими они были бы, если бы не было внешне сгенерированного поля, действующего неравномерно в данной точке и в центре эталонного тела. Внешне сгенерированное поле обычно создается возмущающее третье тело, часто Солнце или Луна в частых примерах - это точки на поверхности Земли или над ней в геоцентрической системе отсчета.)

Для приливного ускорения не требуется вращения или движения тел по орбите; например, тело может быть свободное падение по прямой под действием гравитационного поля, но все еще находясь под влиянием (изменяющегося) приливного ускорения.

К Закон всемирного тяготения Ньютона и законы движения, тело массы м на расстоянии р из центра сферы масс M чувствует силу ${displaystyle {vec {F}} _ {g}}$,

${displaystyle {vec {F}} _ {g} = - {hat {r}} ~ G ~ {frac {Mm} {R ^ {2}}}}$

эквивалент ускорения ${displaystyle {vec {a}} _ {g}}$,

${displaystyle {vec {a}} _ {g} = - {hat {r}} ~ G ~ {frac {M} {R ^ {2}}}}$

куда ${displaystyle {hat {r}}}$ это единичный вектор указывая от тела M к телу м (здесь ускорение от м к M имеет отрицательный знак).

Рассмотрим теперь ускорение, вызываемое сферой массы M испытываемая частицей в непосредственной близости от тела массы м. С р как расстояние от центра M к центру м, пусть ∆р быть (относительно малым) расстоянием частицы от центра тела массы м. Для простоты расстояния сначала рассматриваются только в направлении, указывающем на сферу массы или от нее. M. Если тело массы м сам является сферой радиуса ∆р, то рассматриваемая новая частица может находиться на ее поверхности на расстоянии (р ± ∆r) из центра сферы масс M, и ∆r можно считать положительным, если расстояние частицы от M больше, чем р. Не говоря уже об ускорении свободного падения, которое может испытывать частица в направлении м из-за м'собственной массы, у нас есть ускорение частицы за счет силы тяжести в направлении M в качестве:

${displaystyle {vec {a}} _ {g} = - {hat {r}} ~ G ~ {frac {M} {(Delta Rpm r) ^ {2}}}}$

Вытаскивая р² член из знаменателя дает:

${displaystyle {vec {a}} _ {g} = - {hat {r}} ~ G ~ {frac {M} {R ^ {2}}} ~ {frac {1} {left (1pm {frac {Delta r} {R}} право) ^ {2}}}}$

В Серия Маклорена из ${displaystyle 1 / (13:00 x) ^ {2}}$ является ${displaystyle 1mp 2x + 3x ^ {2} mp cdots}$ что дает расширение в ряд:

${displaystyle {vec {a}} _ {g} = - {hat {r}} ~ G ~ {frac {M} {R ^ {2}}} pm {hat {r}} ~ G ~ {frac {2M } {R ^ {2}}} ~ {frac {Delta r} {R}} + cdots}$

Первый член - это ускорение свободного падения из-за M в центре эталонного тела ${displaystyle m}$, т.е. в точке, где ${displaystyle Delta r}$ равно нулю. Этот член не влияет на наблюдаемое ускорение частиц на поверхности м потому что в отношении M, м (и все на его поверхности) находится в свободном падении. Когда сила, действующая на дальней частицу, вычитается из силы, действующей на ближнюю частицу, этот первый член сокращается, как и все другие члены четного порядка. Остальные (остаточные) члены представляют собой разницу, упомянутую выше, и являются членами приливной силы (ускорения). Когда ∆р маленький по сравнению с р, члены после первого остаточного члена очень малы и им можно пренебречь, что дает приблизительное приливное ускорение ${displaystyle {vec {a}} _ {t, {ext {axial}}}}$ для расстояний ∆р считается, по оси, соединяющей центры м и M:

${displaystyle {vec {a}} _ {t, {ext {axial}}} приблизительно pm {hat {r}} ~ 2Delta r ~ G ~ {frac {M} {R ^ {3}}}}$

При таком расчете для случая, когда ∆р - расстояние по оси, соединяющей центры м и M, ${displaystyle {vec {a}} _ {t}}$ направлен наружу от центра м (где ∆р равно нулю).

Приливные ускорения также могут быть рассчитаны вдали от оси, соединяющей тела. м и M, требуя вектор расчет. В плоскости, перпендикулярной этой оси, приливное ускорение направлено внутрь (к центру, где ∆р равен нулю), а его величина равна ${extstyle {frac {1} {2}} left | {vec {a}} _ {t, {ext {axial}}} ight |}$ в линейном приближении, как на рисунке 4.

Приливные ускорения у поверхностей планет Солнечной системы обычно очень малы. Например, лунное приливное ускорение у поверхности Земли вдоль оси Луна – Земля составляет около 1.1×10⁻⁷ грамм, а солнечное приливное ускорение у поверхности Земли вдоль оси Солнце – Земля составляет около 0.52×10⁻⁷ грамм, куда грамм это гравитационное ускорение на поверхности Земли. Следовательно, сила прилива (ускорение), создаваемая Солнцем, составляет около 45% от силы, создаваемой Луной.^[15] Солнечное приливное ускорение у поверхности Земли было впервые дано Ньютоном в Principia.^[16]

Смотрите также

• Приливный тензор
• Амфидромная точка
• Нарушенная планета
• Галактический прилив
• Приливный резонанс
• Кривизна пространства-времени

Рекомендации

внешняя ссылка

• Гравитационные приливы Дж. Кристофера Михоса из Кейс Вестерн Резервный университет
• Аудио: Каин / Гей - Астрономический состав Приливные силы - июль 2007 г.
• Грей, Меган; Меррифилд, Майкл. "Приливные силы". Шестьдесят символов. Брэди Харан для Ноттингемский университет.
• Пау Амаро Сеоане. «Столкновения звезд: приливное разрушение звезды массивной черной дырой». Получено 2018-12-28.
• Мифы о гравитации и приливах Миколай Савицкий из Колледжа Джона А. Логана и Университета Колорадо.
• Приливные заблуждения Дональд Э. Симанек