WikiDer > Релятивистский эффект Доплера

Рис. 1. Источник световых волн, движущийся вправо относительно наблюдателей со скоростью 0,7c. Частота выше для наблюдателей справа и ниже для наблюдателей слева.

В релятивистский эффект Доплера изменение в частота (и длина волны) света, вызванного относительным движением источника и наблюдателя (как в классическом Эффект Допплера) с учетом эффектов, описываемых специальная теория относительности.

Релятивистский эффект Доплера отличается от нерелятивистского Эффект Допплера поскольку уравнения включают замедление времени эффект специальная теория относительности и не использовать среду распространения в качестве ориентира. Они описывают полную разницу наблюдаемых частот и обладают требуемым Симметрия Лоренца.

Астрономам известны три источника красное смещение/синее смещение: Доплеровские сдвиги; гравитационное красное смещение (из-за выхода света из гравитационного поля); и космологическое расширение (где тянется само пространство). Эта статья касается только доплеровских сдвигов.

Резюме основных результатов

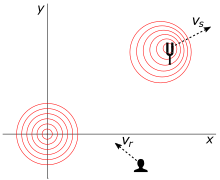
В следующей таблице предполагается, что для ${ displaystyle beta> 0}$ приемник и источник удаляются друг от друга.

Сценарий	Формула	Примечания
Релятивистский продольный Эффект Допплера	${ displaystyle { frac { lambda _ {r}} { lambda _ {s}}} = { frac {f_ {s}} {f_ {r}}} = { sqrt { frac {1+) beta} {1- beta}}}}$
Поперечный эффект Доплера, геометрическая близость	${ displaystyle f_ {r} = gamma f_ {s}}$	Синий сдвиг
Поперечный эффект Доплера, визуально близкий подход	${ displaystyle f_ {r} = { frac {f_ {s}} { gamma}}}$	Красное смещение
TDE, приемник по кругу движение вокруг источника	${ displaystyle f_ {r} = gamma f_ {s}}$	Синий сдвиг
TDE, источник в циркуляре движение вокруг приемника	${ displaystyle f_ {r} = { frac {f_ {s}} { gamma}}}$	Красное смещение
TDE, источник и приемник в круговом движении вокруг общий центр	${ displaystyle { frac { nu '} { nu}} = left ({ frac {1-R ^ {2} omega ^ {2}} {1-R' ^ {2} omega ^ {2}}} right) ^ {1/2}}$	Без доплеровского сдвига когда ${ Displaystyle R = R '}$
Движение в произвольном направлении измеряется в корпусе приемника	${ displaystyle f_ {r} = { frac {f_ {s}} { gamma left (1+ beta cos theta _ {r} right)}}}$
Движение в произвольном направлении измеряется в исходном кадре	${ displaystyle f_ {r} = gamma left (1- beta cos theta _ {s} right) f_ {s}}$

Вывод

Релятивистский продольный эффект Доплера

Релятивистский доплеровский сдвиг для продольного случая, когда источник и приемник движутся прямо навстречу друг другу или от них, часто выводится так, как если бы это было классическое явление, но модифицировалось добавлением замедление времени срок.^[1][2] Это подход, используемый в учебниках по физике или механике для первого года обучения, таких как книги Фейнмана.^[3] или Морен.^[4]

Следуя этому подходу к выводу релятивистского продольного эффекта Доплера, предположим, что приемник и источник движутся прочь друг от друга с относительной скоростью ${ displaystyle v ,}$ при измерении наблюдателем на приемнике или источнике (принятое здесь соглашение о знаках ${ displaystyle v ,}$ является отрицательный если приемник и источник движутся к друг друга).

Рассмотрим проблему в система отсчета источника.

Предположим, что один волновой фронт приходит к получателю. Следующий волновой фронт тогда находится на расстоянии ${ displaystyle lambda _ {s} = c / f_ {s} ,}$ вдали от приемника (где ${ displaystyle lambda _ {s} ,}$ это длина волны, ${ displaystyle f_ {s} ,}$ это частота волн, излучаемых источником, и ${ displaystyle c ,}$ это скорость света).

Волновой фронт движется со скоростью ${ displaystyle c ,}$, но при этом приемник удаляется со скоростью ${ displaystyle v}$ в течение времени ${ displaystyle t_ {s} = 1 / f_ {s} = lambda _ {s} / c}$, так

$${ displaystyle lambda _ {s} + vt_ {r, s} = ct_ {r, s} Longleftrightarrow lambda _ {s} = ct_ {r, s} (1-v / c) Longleftrightarrow t_ {r , s} = { frac {1} {f_ {s} (1- beta)}},}$$

${ Displaystyle бета = v / с ,}$

${ displaystyle t_ {r, s}}$

${ displaystyle f_ {r, s}}$

${ displaystyle f_ {r, s} = 1 / t_ {r, s} = f_ {s} (1- beta).}$

До сих пор уравнения были идентичны уравнениям классического эффекта Доплера с неподвижным источником и движущимся приемником.

Однако из-за релятивистских эффектов часы на приемнике время замедлено относительно часов в источнике: ${ displaystyle t_ {r} = t_ {r, s} / gamma}$, где ${ textstyle gamma = 1 / { sqrt {1- beta ^ {2}}}}$ это Фактор Лоренца. Чтобы узнать, какое время замедлено, напомним, что ${ displaystyle t_ {r, s}}$ - время в кадре, в котором источник находится в покое. Приемник будет измерять принимаемую частоту, чтобы

Уравнение 1:    ${ displaystyle f_ {r} = f_ {r, s} gamma}$ ${ displaystyle = { frac {1- beta} { sqrt {1- beta ^ {2}}}} е_ {s}}$ ${ displaystyle = { sqrt { frac {1- beta} {1+ beta}}} , f_ {s}.}$

Соотношение

${ displaystyle { frac {f_ {s}} {f_ {r}}} = { sqrt { frac {1+ beta} {1- beta}}}}$

называется Фактор Доплера источника относительно приемника. (Эта терминология особенно распространена в теме астрофизика: видеть релятивистское излучение.)

Соответствующие длины волн связаны

Уравнение 2:    ${ displaystyle { frac { lambda _ {r}} { lambda _ {s}}} = { frac {f_ {s}} {f_ {r}}} = { sqrt { frac {1+) beta} {1- beta}}},}$

Идентичные выражения для релятивистского доплеровского сдвига получаются при проведении анализа в системе отсчета приемник с движущимся источником. Это соответствует ожиданиям принцип относительности, что означает, что результат не может зависеть от того, какой объект считается покоящимся. Напротив, классический нерелятивистский эффект Доплера является в зависимости от того, является ли источник или приемник неподвижным по отношению к среде.^[3][4]

Поперечный эффект Доплера

Предположим, что источник и приемник приближаются друг к другу в равномерном инерционном движении по траекториям, которые не сталкиваются. В поперечный эффект Доплера (TDE) может относиться к (а) номинальной синее смещение предсказано специальная теория относительности это происходит, когда излучатель и приемник находятся в точках наибольшего сближения; или (б) номинальный красное смещение предсказывается специальной теорией относительности, когда приемник видит эмиттер как наиболее близкий к нему.^[4] Поперечный эффект Доплера - одно из главных новых предсказаний специальной теории относительности.

Описывается ли в научном отчете TDE как красное или синее смещение, зависит от конкретных деталей экспериментальной схемы. Например, в первоначальном описании TDE Эйнштейном в 1907 г. описывался экспериментатор, смотрящий на центр (ближайшую точку) пучка "лучи канала"(пучок положительных ионов, который создается некоторыми типами газоразрядных трубок). Согласно специальной теории относительности, частота испускания движущихся ионов будет уменьшена на коэффициент Лоренца, так что принимаемая частота будет уменьшена (с красным смещением) тем же фактором.^{[стр. 1][примечание 1]}

С другой стороны, Kündig (1963) описал эксперимент, в котором Мессбауэровский поглотитель вращалась по быстрому круговому пути вокруг центрального мессбауэровского излучателя.^{[стр. 3]} Как поясняется ниже, эта экспериментальная схема привела к измерению синего смещения Кундигом.

Источник и приемник находятся в точках наибольшего сближения

Рис. 2. Источник и приемник находятся в точках наибольшего сближения. (а) Анализ в кадре приемника. (б) Анализ в рамках источника.

В этом сценарии точка наибольшего сближения не зависит от кадра и представляет собой момент, когда расстояние не меняется во времени. Рисунок 2 демонстрирует, что простота анализа этого сценария зависит от кадра, в котором он анализируется.^[4]

• Рис. 2а. Если мы проанализируем сценарий в кадре приемника, то обнаружим, что анализ сложнее, чем должен быть. Видимое положение небесного объекта смещено от его истинного положения (или геометрического положения) из-за движения объекта за время, необходимое его свету, чтобы достичь наблюдателя. Источник будет растянут по времени относительно приемника, но красное смещение, подразумеваемое этим замедлением времени, будет компенсировано синим смещением из-за продольной составляющей относительного движения между приемником и видимым положением источника.
• Рис. 2б. Намного проще, если вместо этого мы проанализируем сценарий с кадра источника. Наблюдатель, находящийся у источника, знает из постановки задачи, что приемник находится ближе всего к нему. Это означает, что приемник не имеет продольной составляющей движения, что усложняет анализ. (т. е. dr / dt = 0, где r - расстояние между приемником и источником) Поскольку часы приемника растянуты по времени относительно источника, свет, который получает приемник, смещен в синий цвет с коэффициентом гамма. Другими словами,

Уравнение 3:    ${ displaystyle f_ {r} = gamma f_ {s}}$

Получатель видит источник как ближайший к нему

Рисунок 3. Поперечный доплеровский сдвиг для сценария, когда приемник видит источник как ближайший к нему.

Этот сценарий эквивалентен тому, что приемник смотрит под прямым углом к ​​пути источника. Анализ этого сценария лучше всего проводить с кадра приемника. На рисунке 3 показано, что приемник освещается светом, когда источник находился ближе всего к приемнику, даже если источник переместился дальше.^[4] Поскольку часы источника имеют замедленное время, измеренное в кадре приемника, и поскольку нет продольной составляющей его движения, свет от источника, испускаемый из этой ближайшей точки, смещается в красную область с частотой

Уравнение 4:    ${ displaystyle f_ {r} = { frac {f_ {s}} { gamma}}}$

В литературе большинство сообщений о поперечном доплеровском сдвиге анализируют эффект с точки зрения приемника, направленного под прямым углом к ​​пути источника, таким образом, видя источник находится в ближайшей точке и наблюдает красное смещение.

Точка нулевого сдвига частоты

Рис. 4. Сдвиг нулевой частоты происходит для импульса, который проходит кратчайшее расстояние от источника до приемника.

Учитывая, что в случае, когда инерционно движущиеся источник и приемник геометрически находятся на их ближайшем приближении друг к другу, приемник наблюдает синее смещение, тогда как в случае, когда приемник видит если источник находится в ближайшей точке, приемник наблюдает красное смещение, очевидно, должна существовать точка, в которой синее смещение переходит в красное. На рис. 2 сигнал проходит перпендикулярно тракту приемника и смещен в синюю сторону. На рис. 3 сигнал проходит перпендикулярно пути источника и смещен в красную сторону.

Как видно на рис. 4, сдвиг нулевой частоты происходит для импульса, который проходит кратчайшее расстояние от источника до приемника. Если смотреть в кадре, где источник и приемник имеют одинаковую скорость, этот импульс излучается перпендикулярно пути источника и принимается перпендикулярно пути приемника. Импульс излучается незадолго до точки наибольшего сближения и принимается немного позже.^[5]

Один объект совершает круговое движение вокруг другого

Рис. 5. Поперечный эффект Доплера для двух сценариев: (а) приемник движется по кругу вокруг источника; (б) источник движется по кругу вокруг приемника.

Рис. 5 иллюстрирует два варианта этого сценария. Оба варианта можно проанализировать, используя простые аргументы, связанные с замедлением времени.^[4] Рисунок 5a по существу эквивалентен сценарию, описанному на рисунке 2b, и приемник видит свет от источника как с синим смещением в несколько раз. ${ displaystyle gamma}$. Рисунок 5b по существу эквивалентен сценарию, описанному на рисунке 3, и свет смещен в красную сторону.

Единственная кажущаяся сложность заключается в том, что орбитальные объекты находятся в ускоренном движении. У ускоренной частицы нет инерциальной системы отсчета, в которой она всегда покоится. Однако всегда можно найти инерциальную систему отсчета, которая мгновенно движется вместе с частицей. Этот кадр, мгновенно движущаяся система отсчета (MCRF), позволяет применять специальную теорию относительности к анализу ускоренных частиц. Если инерциальный наблюдатель смотрит на ускоряющиеся часы, при вычислении замедления времени важна только мгновенная скорость часов.^[6]

Обратное, однако, неверно. Анализ сценариев, в которых обе объекты, находящиеся в ускоренном движении, требуют более сложного анализа. Непонимание этого момента привело к путанице и недопониманию.

Источник и приемник совершают круговое движение вокруг общего центра.

Рисунок 6. Источник и приемник расположены на противоположных концах ротора, на равном расстоянии от центра.

Предположим, что источник и приемник расположены на противоположных концах вращающегося ротора, как показано на рис. 6. Кинематические аргументы (специальная теория относительности) и аргументы, основанные на том, что нет разницы потенциалов между источником и приемником в псевдогравитационном поле ротора. (общая теория относительности) оба приводят к выводу, что не должно быть доплеровского сдвига между источником и приемником.

В 1961 году Чампени и Луна провел Мессбауэровский эксперимент с ротором проверив именно этот сценарий, и обнаружил, что на процесс мессбауэровского поглощения не влияет вращение.^{[стр. 4]} Они пришли к выводу, что их результаты подтверждают специальную теорию относительности.

Этот вывод вызвал некоторые противоречия. Один настойчивый критик теории относительности утверждал, что, хотя эксперимент соответствовал общей теории относительности, он опровергал специальную теорию относительности, его точка зрения заключалась в том, что, поскольку излучатель и поглотитель находились в однородном относительном движении, специальная теория относительности требовала наблюдения доплеровского сдвига. Ошибочность аргумента этого критика была, как показано в разделе Точка нулевого сдвига частоты, что это просто неправда, что доплеровский сдвиг всегда должен наблюдаться между двумя кадрами в однородном относительном движении.^[7] Кроме того, как показано в разделе Источник и приемник находятся в точках наибольшего сближения, сложность анализа релятивистского сценария часто зависит от выбора системы отсчета. Попытка проанализировать сценарий в рамках приемника требует очень утомительной алгебры. Гораздо проще, почти тривиально установить отсутствие доплеровского сдвига между эмиттером и поглотителем в лабораторной раме.^[7]

На самом деле, однако, эксперимент Чампени и Муна ничего не сказал ни за, ни против специальной теории относительности. Из-за симметрии установки оказывается, что практически любой возможная теория доплеровского сдвига между кадрами при равномерном инерционном движении должна дать нулевой результат в этом эксперименте.^[7]

Вместо того чтобы быть равноудаленными от центра, предположим, что эмиттер и поглотитель находятся на разных расстояниях от центра ротора. Для излучателя на радиусе ${ displaystyle R '}$ и поглотитель на радиусе ${ displaystyle R}$ куда угодно на роторе отношение частоты эмиттера, ${ displaystyle nu ',}$ и частота поглотителя, ${ displaystyle nu,}$ дан кем-то

Уравнение 5:    ${ displaystyle { frac { nu '} { nu}} = left ({ frac {1-R ^ {2} omega ^ {2}} {1-R' ^ {2} omega ^ {2}}} right) ^ {1/2}}$

где ${ displaystyle omega}$ - угловая скорость ротора. Источник и излучатель не обязательно должны находиться на расстоянии 180 ° друг от друга, но могут располагаться под любым углом по отношению к центру.^{[стр. 5][8]}

Движение в произвольном направлении

Рис. 7. Доплеровский сдвиг при движении источника под произвольным углом по отношению к линии между источником и приемником.

Анализ, использованный в разделе Релятивистский продольный эффект Доплера может быть расширен прямым способом для вычисления доплеровского сдвига для случая, когда инерционные движения источника и приемника происходят под любым заданным углом.^[2][9]На рис.7 представлен сценарий из кадра приемника, при котором источник движется со скоростью ${ displaystyle v}$ под углом ${ displaystyle theta _ {r}}$ измеряется в рамке ствольной коробки. Радиальная составляющая движения источника по лучу зрения равна ${ displaystyle v cos { theta _ {r}}.}$

Приведенное ниже уравнение можно интерпретировать как классический доплеровский сдвиг для неподвижного и движущегося источника, модифицированный с помощью фактора Лоренца. ${ displaystyle gamma:}$

Уравнение 6:    ${ displaystyle f_ {r} = { frac {f_ {s}} { gamma left (1+ beta cos theta _ {r} right)}}.}.$

В случае, когда ${ displaystyle theta _ {r} = 90 ^ { circ}}$, получаем поперечный эффект Доплера:

${ displaystyle f_ {r} = { frac {f_ {s}} { gamma}}. ,}$

В своей статье 1905 года по специальной теории относительности^{[стр. 2]} Эйнштейн получил несколько иное уравнение для уравнения доплеровского сдвига. После изменения имен переменных в уравнении Эйнштейна, чтобы они соответствовали используемым здесь, его уравнение выглядит следующим образом:

Уравнение 7:    ${ displaystyle f_ {r} = gamma left (1- beta cos theta _ {s} right) f_ {s}.}$

Различия связаны с тем, что Эйнштейн оценил угол ${ displaystyle theta _ {s}}$ относительно источника покоя, а не приемник покоя. ${ displaystyle theta _ {s}}$ не равно ${ displaystyle theta _ {r}}$ из-за эффекта релятивистская аберрация. Уравнение релятивистской аберрации:

Уравнение 8:    ${ displaystyle cos theta _ {r} = { frac { cos theta _ {s} - beta} {1- beta cos theta _ {s}}} ,}$

Подставляя релятивистское уравнение аберрации Уравнение 8 в Уравнение 6 дает Уравнение 7, демонстрируя согласованность этих альтернативных уравнений для доплеровского сдвига.^[9]

Настройка ${ displaystyle theta _ {r} = 0}$ в Уравнение 6 или ${ displaystyle theta _ {s} = 0}$ в Уравнение 7 дает Уравнение 1, выражение для релятивистского продольного доплеровского сдвига.

Четырехвекторный подход к получению этих результатов можно найти в работе Ландау и Лифшица (2005).^[10]

Визуализация

Рис. 8. Сравнение релятивистского эффекта Доплера (вверху) с нерелятивистским эффектом (внизу).

Рис. 8 помогает нам понять, в грубом качественном смысле, как релятивистский эффект Доплера и релятивистская аберрация отличаются от нерелятивистских Эффект Допплера и нерелятивистские аберрация света. Предположим, что наблюдатель равномерно окружен во всех направлениях желтыми звездами, излучающими монохроматический свет с длиной волны 570 нм. Стрелки на каждой диаграмме представляют вектор скорости наблюдателя относительно окружающей его среды с величиной 0,89.c.

• В нерелятивистском случае свет впереди наблюдателя смещается в синюю сторону до длины волны 300 нм в среднем ультрафиолете, а свет позади наблюдателя смещается в красную сторону до 5200 нм в промежуточном инфракрасном диапазоне. Из-за аберрации света объекты, которые раньше находились под прямым углом к ​​наблюдателю, кажутся смещенными вперед на 42 °.
• В релятивистском случае свет впереди наблюдателя смещается в синюю сторону до длины волны 137 нм в дальнем ультрафиолете, а свет позади наблюдателя смещается в красную сторону до 2400 нм в коротковолновой инфракрасной области. Из-за релятивистской аберрации света объекты, ранее находившиеся под прямым углом к ​​наблюдателю, кажутся смещенными вперед на 63 °.
• В обоих случаях монохроматические звезды впереди и позади наблюдателя имеют доплеровский сдвиг в сторону невидимых длин волн. Однако если бы у наблюдателя были глаза, которые могли видеть в ультрафиолете и инфракрасном диапазоне, он бы увидел звезды впереди себя ярче и теснее сгруппированных вместе, чем звезды позади, но звезды были бы намного ярче и гораздо более концентрированными в релятивистский случай.^[11]

Настоящие звезды не монохроматичны, а излучают волны в диапазоне длин волн, приближающемся к черное тело распространение. Необязательно, чтобы звезды перед наблюдателем имели более синий цвет. Это связано с смещением всего спектрального распределения энергии. В то же время, когда видимый свет смещается в сторону невидимого ультрафиолета, инфракрасный свет смещается в сторону видимого диапазона. Какие именно изменения в цветах человек видит, зависит от физиологии человеческого глаза и от спектральных характеристик наблюдаемых источников света.^[12][13]

Эффект Доплера по интенсивности

Эффект Доплера (с произвольным направлением) также изменяет воспринимаемую интенсивность источника: это можно кратко выразить тем фактом, что сила источника, деленная на куб частоты, является инвариантом Лоренца.^{[стр. 6][заметка 2]} Это означает, что общая интенсивность излучения (сумма по всем частотам) умножается на четвертую степень доплеровского фактора частоты.

Как следствие, поскольку Закон планка описывает излучение черного тела как имеющий спектральную интенсивность по частоте, пропорциональную ${ Displaystyle ню ^ {3} / влево (е ^ {ч ню / кТ} -1 вправо)}$ (куда Т - температура источника и ν частота), можно сделать вывод, что спектр черного тела, видимый через доплеровский сдвиг (с произвольным направлением), по-прежнему является спектром черного тела с температурой, умноженной на тот же коэффициент Доплера, что и частота.

Этот результат дает одно из свидетельств того, что Теория большого взрыва из альтернативных теорий, предложенных для объяснения космологическое красное смещение.^[14]

Экспериментальная проверка

Поскольку поперечный эффект Доплера является одним из основных новых предсказаний специальной теории относительности, обнаружение и точное количественное определение этого эффекта было важной целью экспериментов, пытающихся подтвердить специальную теорию относительности.

Измерения типа Айвса и Стилвелла

Рис. 9. Почему сложно точно измерить поперечный эффект Доплера с помощью поперечного пучка.

Эйнштейн (1907) первоначально предположил, что TDE можно измерить, наблюдая луч "лучи канала"под прямым углом к ​​балке.^{[стр. 1]} Попытки измерить TDE по этой схеме показали, что это непрактично, поскольку максимальная скорость пучка частиц, доступная в то время, составляла всего несколько тысячных скорости света.

На рис.9 показаны результаты попытки измерения линии 4861 Ангстрема, излучаемой пучком канальных лучей (смесь ионов H1 +, H2 + и H3 +), когда они рекомбинируют с электронами, оторванными от разбавленного газообразного водорода, используемого для заполнения канального луча. трубка.Здесь предсказанный результат TDE представляет собой линию 4861,06 Ангстрема. Слева продольный доплеровский сдвиг приводит к уширению эмиссионной линии до такой степени, что TDE невозможно наблюдать. Средние рисунки показывают, что даже если сузить обзор до точного центра луча, очень небольшие отклонения луча от точного прямого угла вызывают сдвиги, сопоставимые с предсказанным эффектом.

Вместо того, чтобы пытаться напрямую измерить TDE, Айвз и Стилуэлл (1938) использовали вогнутое зеркало, которое позволяло им одновременно наблюдать почти продольный прямой луч (синий) и его отраженное изображение (красный). Спектроскопически можно было наблюдать три линии: несмещенную эмиссионную линию и линии с синим и красным смещением. Среднее значение линий с красным и синим смещением можно сравнить с длиной волны несмещенной линии излучения. Разница, которую измерили Айвз и Стилвелл, в экспериментальных пределах соответствовала эффекту, предсказанному специальной теорией относительности.^{[стр. 7]}

Различные последующие повторения эксперимента Айвса и Стилуэлла использовали другие стратегии для измерения среднего значения излучения пучка частиц с синим и красным смещением. В некоторых недавних повторениях эксперимента использовалась современная технология ускорителей, чтобы организовать наблюдение двух противоположно вращающихся пучков частиц. В других повторениях энергии гамма-лучей, испускаемых быстро движущимся пучком частиц, измерялись под противоположными углами по отношению к направлению пучка частиц. Поскольку в этих экспериментах фактически не измеряется длина волны пучка частиц под прямым углом к ​​пучку, некоторые авторы предпочитают называть измеряемый ими эффект «квадратичным доплеровским сдвигом», а не TDE.^{[стр. 8][стр. 9]}

Прямое измерение поперечного эффекта Доплера

Появление ускоритель частиц Технология сделала возможным получение пучков частиц со значительно большей энергией, чем это было доступно Айвзу и Стилуэллу. Это позволило разработать тесты поперечного эффекта Доплера непосредственно в соответствии с тем, как Эйнштейн первоначально их представлял, то есть путем прямого наблюдения пучка частиц под углом 90 °. Например, Hasselkamp et al. (1979) наблюдали ЧАСЛиния α, излучаемая атомами водорода, движущимися со скоростью от 2,53 × 10⁸ см / с до 9,28 × 10⁸ см / с, найдя коэффициент при члене второго порядка в релятивистском приближении равным 0,52 ± 0,03, что прекрасно согласуется с теоретическим значением 1/2.^{[стр. 10]}

Другие прямые испытания TDE на вращающихся платформах стали возможными благодаря открытию Эффект Мёссбауэра, что позволяет получать чрезвычайно узкие резонансные линии для излучения и поглощения ядерного гамма-излучения.^[15] Эксперименты с эффектом Мёссбауэра доказали, что легко могут обнаруживать TDE с использованием относительных скоростей излучатель-поглотитель порядка 2 × 10⁴ см / с. Эти эксперименты включают эксперименты, выполненные Хэем. и другие. (1960),^{[стр. 11]} Champeney и другие. (1965),^{[стр. 12]} и Кюндиг (1963).^{[стр. 3]}

Измерения замедления времени

Поперечный эффект Доплера и кинематическое замедление времени специальной теории относительности тесно связаны. Все проверки TDE представляют собой проверки кинематического замедления времени, и большинство проверок кинематического замедления времени также представляют проверки TDE. Интернет-ресурс "Что является экспериментальной основой специальной теории относительности?" задокументировал с краткими комментариями многие тесты, которые на протяжении многих лет использовались для подтверждения различных аспектов специальной теории относительности.^[16] Kaivola et al. (1985)^{[стр. 13]} и McGowan et al. (1993)^{[стр. 14]} являются примерами экспериментов, классифицированных в этом ресурсе как эксперименты с замедлением времени. Эти два также представляют собой тесты TDE. В этих экспериментах сравнивали частоту двух лазеров, один из которых привязан к частоте перехода атома неона в быстром пучке, а другой - к тому же переходу в тепловом неоне. Версия эксперимента 1993 года подтвердила замедление времени и, следовательно, TDE, с точностью 2,3 × 10⁻⁶.

Релятивистский эффект Доплера для звука и света

Рис. 10. Формула релятивистского доплеровского сдвига применима как к звуку, так и к свету.

Учебники по физике первого года обучения почти всегда анализируют доплеровский сдвиг для звука с точки зрения ньютоновской кинематики, а доплеровский сдвиг для света и электромагнитных явлений - с точки зрения релятивистской кинематики. Это создает ложное впечатление, что акустические явления требуют другого анализа, чем свет и радиоволны.

Традиционный анализ эффекта Доплера для звука представляет собой низкоскоростное приближение к точному релятивистскому анализу. Полностью релятивистский анализ звука фактически в равной степени применим как к звуковым, так и к электромагнитным явлениям.

Рассмотрим пространственно-временную диаграмму на рис. 10. На этой диаграмме показаны мировые линии для камертона (источника) и приемника. События О и А представляют собой два колебания камертона. Период вилки - это величина OA, и обратный наклон AB представляет скорость распространения сигнала (то есть скорость звука) до события B. Поэтому мы можем написать:^[9]

${ displaystyle c_ {s} = { frac {x_ {B} -x_ {A}} {t_ {B} -t_ {A}}}}$ (скорость звука)

${ displaystyle v_ {s} = - { frac {x_ {A}} {t_ {A}}}}$        ${ displaystyle v_ {r} = { frac {x_ {B}} {t_ {B}}}}$ (скорости источника и приемника)

${ displaystyle | OA | = { sqrt {t_ {A} ^ {2} - (x_ {A} / c) ^ {2}}}}$

${ displaystyle | OB | = { sqrt {t_ {B} ^ {2} - (x_ {B} / c) ^ {2}}}}$

${ displaystyle v_ {s}}$ и ${ displaystyle v_ {r}}$ предполагается меньше, чем ${ displaystyle c_ {s},}$ поскольку в противном случае их прохождение через среду приведет к возникновению ударных волн, что сделает расчет недействительным. Некоторая рутинная алгебра дает соотношение частот:

Уравнение 9:    ${ displaystyle { frac {f_ {r}} {f_ {s}}} = { frac {| OA |} {| OB |}}}$ ${ displaystyle = { frac {1-v_ {r} / c_ {s}} {1 + v_ {s} / c_ {s}}} { sqrt { frac {1- (v_ {s} / c ) ^ {2}} {1- (v_ {r} / c) ^ {2}}}}}$

Если ${ displaystyle v_ {r}}$ и ${ displaystyle v_ {s}}$ малы по сравнению с ${ displaystyle c}$, приведенное выше уравнение сводится к классической формуле Доплера для звука.

Если скорость распространения сигнала ${ displaystyle c_ {s}}$ подходы ${ displaystyle c}$, можно показать, что абсолютные скорости ${ displaystyle v_ {s}}$ и ${ displaystyle v_ {r}}$ источника и приемника сливаются с единой относительной скоростью, независимо от какой-либо привязки к фиксированной среде. Действительно, получаем Уравнение 1, формула для релятивистского продольного доплеровского сдвига.^[9]

Анализ пространственно-временной диаграммы на рис. 10 дал общую формулу для источника и приемника, движущихся непосредственно вдоль луча зрения, то есть коллинеарно.

Рис. 11. Источник и приемник движутся в разных направлениях и с разными скоростями в кадре, где скорость звука не зависит от направления.

Рис. 11 иллюстрирует сценарий в двух измерениях. Источник движется со скоростью ${ Displaystyle mathbf {v_ {s}}}$ (на момент выпуска). Он излучает сигнал, который движется со скоростью ${ displaystyle mathbf {C}}$ к приемнику, который движется со скоростью ${ Displaystyle mathbf {v_ {r}}}$ во время приема. Анализ выполняется в системе координат, в которой скорость сигнала ${ displaystyle | mathbf {C} |}$ не зависит от направления.^[5]

Соотношение между собственными частотами для источника и приемника равно

Уравнение 10:    ${ displaystyle { frac {f_ {r}} {f_ {s}}} = { frac {1 - { frac {| mathbf {v_ {r}} |} { mathbf {| C |}} } cos ( theta _ { mathbf {C, v_ {r}}})} {1 - { frac {| mathbf {v_ {s}} |} { mathbf {| C |}}} cos ( theta _ { mathbf {C, v_ {s}}})}} { sqrt { frac {1- (v_ {s} / c) ^ {2}} {1- (v_ {r} / c) ^ {2}}}}}$

Ведущее отношение имеет форму классического эффекта Доплера, а член квадратного корня представляет собой релятивистскую поправку. Если рассматривать углы относительно рамки источника, то ${ displaystyle v_ {s} = 0}$ и уравнение сводится к Уравнение 7, Формула Эйнштейна 1905 г. для эффекта Доплера. Если рассматривать углы относительно рамы ствольной коробки, то ${ displaystyle v_ {r} = 0}$ и уравнение сводится к Уравнение 6, альтернативная форма уравнения доплеровского сдвига, обсуждаемая ранее.^[5]

Смотрите также

• Эффект Допплера
• Доплеровское излучение
• Красное смещение
• Синий сдвиг
• Замедление времени
• Гравитационное замедление времени
• Специальная теория относительности

Примечания

Основные источники

Рекомендации

дальнейшее чтение

• Морикони, М. (1 ноября 2006 г.). «Специальная теория относительности через эффект Доплера». Европейский журнал физики. 27 (6): 1409–1423. arXiv:физика / 0605204. Bibcode:2006EJPh ... 27.1409M. Дои:10.1088/0143-0807/27/6/015. S2CID 11347287.

внешняя ссылка

• Симулятор специальной теории относительности Warp Компьютерная программа, демонстрирующая релятивистский эффект Доплера.
• Краус, Юте; Зан, Корвин. «Космическое путешествие во времени: визуализация теории относительности». SpacetimeTravel.org. Образовательная группа по физике и астрономии, Университет Хильдесхайма, Германия. Получено 17 октября 2018.