WikiDer > Нелинейная теория полупроводниковых лазеров
эта статья написано как исследовательская статья или научный журнал что может использовать чрезмерно технические термины или не может быть написано как энциклопедическая статья. (Ноябрь 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
Теория лазера полупроводника Фабри-Перо (FP) лазеры оказывается нелинейным, поскольку усиление,[1][2] то показатель преломления[3] и коэффициент потерь[4] функции поток энергии. Нелинейная теория[2] позволили объяснить ряд экспериментов, некоторые из которых даже не могли быть объяснены (например, естественные ширина линии), гораздо реже моделируемый на основе других теоретических моделей; это говорит о том, что разработанная нелинейная теория представляет собой новую парадигму теории лазеров.
Уравнения в усиливающей среде
Уравнения Максвелла описывают поле для пассивной среды и не могут использоваться при описании поля в лазере и квантовый усилитель. Выводятся феноменологические уравнения для электромагнитного поля в получить средний, т.е. уравнения Максвелла для активной среды, и Теорема Пойнтинга для этих уравнений.[1][2][5] Уравнения Максвелла в активной среде используются для получения уравнений для потока энергии и для описания нелинейного фазового эффекта.[1][2][5]
мы определили η как конкретный коэффициент усиления; σ специфичен проводимость описывающий некогерентные потери (например, на свободных электронах). Остальные уравнения Максвелла используются без изменений.
Теорема Пойнтинга следует из (1) - (3):
где S Вектор Пойнтинга; V = sz, 0
Уравнения для потока энергии следуют из (4):
где
где I - поток энергии; s - площадь сечения активной зоны лазера; Г - коэффициент удержания; αв коэффициент поглощения в активной зоне; αвне коэффициент поглощения вне активной зоны; αИкс потери из-за некогерентное рассеяние α2p(I) - коэффициент двухфотонного поглощения,[2][4] и α2p(I) = β⋅I.
Формулы формы линии и естественной ширины линии
Разработана теория естественной ширины линии в полупроводниковых лазерах, из которой следует, что показатель преломления n в FP-лазерах[3][5] и эффективный показатель преломления nef в Распределенная обратная связь (DFB) лазеры[5][6] являются функциями E:
Получены формулы для формы линии в лазерах ФП и РОС. Эти формулы для формы линии аналогичны и имеют следующий вид:
где - частота генерации лазера;
где D0, D1, D2 имеют разную форму для лазеров ФП и РОС[2][6][7][8].[9]Запишем естественную ширину линии Δν[2][8][9]
где - мостовая функция;[2][8][9] и - характерная ширина линии и характерная мощность лазера; k - характерный параметр лазерной нелинейности; q - безразмерная обратная степень:
Самостоятельное значение имеет теория естественной ширины линии в полупроводниковых лазерах. В то же время развитая теория является составной частью нелинейной теории лазеров, а ее концепции и введенные характеристические параметры используются во всех разделах нелинейной теории.
Коэффициент усиления в полупроводниковом лазере
С использованием матрица плотности из уравнений с релаксацией сделаны следующие выводы: спектральный коэффициент Эйнштейна в полупроводниковом лазере и, соответственно, Коэффициент Эйнштейна;[1][2][10] выведена формула для эффекта насыщения в полупроводниковом лазере; было показано, что эффект насыщения в полупроводниковом лазере невелик.[1][2] Коэффициент усиления в полупроводниковом лазере был получен с использованием уравнений матрицы плотности с релаксацией.[1][2] Было обнаружено, что усиление лазера Фабри-Перо зависит от потока энергии, и это определяет «основной нелинейный эффект» в полупроводниковом лазере.
где
где - коэффициент Эйнштейна для индуцированного перехода между двумя уровнями энергии при воздействии узкополосной волны записывается в следующей форме:[2][10]
где эффективная естественная ширина линии; - поток энергии; - спектральная плотность переходов.
Необходимое условие наведенного излучения 1-го рода
Необходимые условия для индуцированного излучения 1-го и 2-го рода определены в.[1][2] Необходимые условия для индуцированного излучения определяются требованием, чтобы коэффициент усиления был больше нуля. Необходимое условие индуцированного излучения 1-го рода, сформулированное Бернаром и Дюрафуром.[2][11] состоит в том, что население уровней, расположенных выше, становится больше, чем население уровней, расположенных ниже
Необходимое условие наведенного излучения 2-го рода
Необходимое условие индуцированного излучения 2-го рода, сформулированное Ноппе.[1][2] в том, что:
Необходимое условие индуцированного излучения 2-го рода позволяет сформулировать основное ограничение мощности лазера:[1][2] что подтверждено экспериментально:
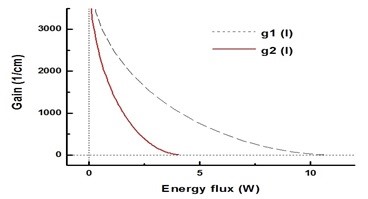
где I - поток энергии; I (M) - характерный параметр предельной мощности. На рис. 1 показана функция g (I) для двух наборов характеристических параметров.
Моделирование экспериментов
4.1. Уравнения Максвелла в активной среде используются для получения уравнений для потока энергии.[1][2][5] Описан и смоделирован нелинейный фазовый эффект.[1][2] с использованием нелинейности показателя преломления.[3] (см. рис.3).
4.2. На основе развитой теории смоделированы экспериментальные выходные характеристики: естественная ширина линии (см. Моделирование в,[2][6]) (см. рис.2), экспериментальные ватт-амперные характеристики[1][2][11] (см. рис.4) и зависимости экспериментальной длины линии выходного излучения от тока в полупроводниковых инжекционных лазерах Фабри-Перо,[1][2] (см. рис.3), а также ширину линии в РОС-лазерах (см. моделирование в[7][8]). Созданная теория позволяет моделировать большинство опубликованных экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо и DFB-лазерах с распределенной обратной связью.[2][6][7][8][9][12] с помощью двух методов (с использованием (13) и (15)). На основе формулы, полученной для формы линии,[2][6] 12 экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо (например, см. Рис.2) и 15 экспериментов в РОС-лазерах[2][9] были смоделированы. На основе формулы, полученной для естественной ширины линии,[2][6][8] 15 экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо[2][6] и 15 экспериментов с РОС-лазерами[2][9] были смоделированы. Полученная формула для формы линии излучения (лазеров FP[2][6][12] и РОС-лазеры[2][7]) отличается от формулы линии Лоренца.
4.3. На основе развитой теории смоделированы экспериментальные выходные характеристики: естественная ширина линии (см. Моделирование в,[5][7]), экспериментальные ватт-амперные характеристики[10] (см. рис.4), а также зависимость экспериментальной длины линии выходного излучения от тока в полупроводниковых инжекционных лазерах Фабри-Перо[13] (см. рис.3), а также ширину линии в РОС-лазерах (см. моделирование в[2][9]).
4.4. На основе нелинейной теории даны рекомендации по созданию лазеров с меньшей естественной шириной линии и лазеров с большей выходной мощностью.[1][2]
Заключение
На основе решения уравнений матрицы плотности получен коэффициент Эйнштейна для индуцированного перехода; было показано, что эффект насыщения для полупроводниковых лазеров невелик.[1][2] Выведена формула усиления в зависимости от потока энергии; это основной нелинейный эффект в лазере. Было заявлено, что основным эффектом, приводящим к нелинейности, является эффект насыщения.[1][2] Для полупроводниковых лазеров эффект насыщения незначителен. Мы получили коэффициент усиления g для полупроводникового лазера Фабри-Перо на основе уравнений матрицы плотности и выражений для естественной ширины линии.[1][2] Таким образом, теория ширины линии[2][8][9] является неотъемлемой частью нелинейной теории. Результирующая зависимость g от потока энергии была названа основным нелинейным эффектом в полупроводниковых лазерах;[1][2] Вывод формулы этого отношения представлен в.[1][2] Экспериментальный сдвиг длины волны в зависимости от нормализованного тока (Дж / Дж) и выходная мощность в зависимости от тока были смоделированы для мощного лазера с квантовой ямой из собственного полупроводника. Учтено уширение плотности состояний из-за различных эффектов. Нелинейная теория позволила объяснить ряд экспериментов, некоторые из которых даже не могли быть объяснены (например, естественная ширина линии), а тем более смоделированы на основе других теоретических моделей; это говорит о том, что разработанная нелинейная теория представляет собой новую парадигму теории лазеров. В связи с развитием нелинейной теории могут быть даны рекомендации по созданию лазеров с меньшей естественной шириной линии и лазеров с большей выходной мощностью.
использованная литература
- ^ а б c d е ж г час я j k л м п о п q р s т ты v ш Ноппе М.Г. О нелинейной теории полупроводниковых лазеров. 2016 Laser Phys. 26055004 (DOI: 10.1088 / 1054-660X / 26/5/055004)
- ^ а б c d е ж г час я j k л м п о п q р s т ты v ш Икс y z аа ab ac объявление ае аф аг ах ай эй ак аль я ан ао ap водный Ноппе М.Г. «Основы нелинейной теории полупроводниковых лазеров» (ИД СО РАН, 2016. Новосибирск, 2016). (Чтобы приобрести монографию, воспользуйтесь следующей ссылкой: «Основы нелинейной теории полупроводниковых лазеров»)
- ^ а б c Партови, Э. М. Гармир, J. Appl. Phys., 69, 6885 (1991).
- ^ а б Саид А.А. и др. Опт. Soc. Am. В 1992 9 405
- ^ а б c d е ж Ноппе М. Г. О нелинейной рефракции в полупроводниковых лазерах; моделирование эксперимента, J. Mod. Опт. 2004 51 153
- ^ а б c d е ж г час я Ноппе М. Г., Естественная ширина линии полупроводниковых лазеров Фабри-Перо, Laser Phys., 24, 125006 (2014). DOI: 10.1088 / 1054-660X / 24/12/125006
- ^ а б c d е Ноппе М. Г. О естественной ширине линии лазеров с распределенной обратной связью; моделирование экспериментов. В Proc. XII Междунар. Конференция. (APEIE - 2014) - т.1, с. 456 - 460)
- ^ а б c d е ж г Ноппе М. Г. О формуле для естественной ширины линии в лазерах Фабри-Перо; моделирование экспериментов В Proc. XII Междунар. Конференция. (APEIE - 2014) - т.1, с. 472 - 477)
- ^ а б c d е ж г час Noppe M G О формуле для естественной ширины линии в лазерах с распределенной обратной связью; моделирование экспериментов. В Proc. XII Междунар. Конференция. (APEIE - 2014) - т.1, с. 461-467
- ^ а б c Ноппе М.Г. Резонансные и нерезонансные коэффициенты вынужденных переходов для системы с релаксацией, Technical Physics Letters 2000, V. 26, 10-11
- ^ а б c Андреев А.Ю. и др. Полупроводники, 2009 г., 43 543-547
- ^ а б Ноппе М.Г. О форме линии и естественной ширине линии; Моделирование и интерпретация экспериментов. В Proc. XII Междунар. Конференция. (НУСОД-2012), 123.
- ^ Бернар М.Г., Дюраффур Дж. Phys. Статус Solidi 127 699
- ^ Эльзассер В., Гобель Э.О., Кул Дж., IEEE JQE, 1983 19 981
- ^ Ито М., Кимура Т. 1980 IEEE J. QE 16 910