WikiDer > Сетка перекрывающихся кругов
| квадратная круглая сетка | |||||
|---|---|---|---|---|---|
| 1+ |  |  |  |  |  |
| 4 |  |  |  |  |  |
| 9 |  |  |  |  |  |
| Центрированные квадратные формы решетки | |||||
| 5 |  |  |  |  |  |
| 13 |  |  |  |  |  |
 |  |  |  |  | |
| сетка из треугольных кругов | |||||
| 1+ |  |  |  |  |  |
| 3 |  |  | 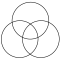 |  |  |
| 4 |  |  |  |  |  |
| 7 | 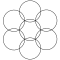 |  |  |  |  |
| 19 |  |  |  |  |  |
 |  |  |  |  | |
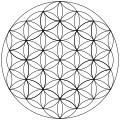
An сетка перекрывающихся кругов это геометрический узор повторение, перекрытие круги равного радиус в двумерное пространство. Обычно дизайны основаны на кругах с центром в треугольники (с простой формой двух кругов, названной vesica piscis) или на квадратная решетка узор точек.
Узоры из семи перекрывающихся кругов появляются на исторических артефактах, начиная с VII века до нашей эры; они становятся часто используемым украшением в Римская империя периода и сохранились в средневековых художественных традициях как в Исламское искусство (гирих украшения) и в Готическое искусство. Название «Цветок Жизни» дано узору перекрывающихся кругов в Нью Эйдж публикации.
Особый интерес представляет шестилепестковая розетка полученный из шаблона «семь перекрывающихся кругов», также известного как «Солнце Альп» из-за его частого использования в альпийских народное искусство в 17-18 веках.
Треугольная сетка перекрывающихся кругов
 |
| Этот узор можно продолжать до бесконечности, здесь можно увидеть шестиугольные кольца из 1, 7, 19, 37, 61, 91 кругов ... |
В треугольная решетка форма, с радиусами окружности равными их разделению, называется сетка из семи перекрывающихся кругов.[1] Он содержит 6 кругов, пересекающихся в одной точке, и 7-й круг с центром на этом пересечении.
Перекрывающиеся круги с аналогичными геометрическими конструкциями нечасто использовались в различных декоративное искусство с древних времен. Шаблон нашел широкое применение в массовой культуре, в мода, ювелирные украшения, татуировки и декоративные изделия.
Культурное значение
Ближний Восток
Самое древнее известное появление узора «перекрывающихся кругов» датируется VII или VI веком до нашей эры. Оно было обнаружено на пороге дворца ассирийского царя. Ашшур-бани-апли в Дур Шаррукин (сейчас в Лувр).[2]
Этот узор становится все более распространенным в первые века нашей эры. Одним из ранних примеров являются пять узоров из 19 перекрывающихся кругов, нарисованных на гранитных колоннах в Храм Осириса в Абидос, Египет,[3] и еще пять на колонне напротив здания. Они нарисованы красным охра а некоторые очень тусклые и трудно различимые.[4]Шаблоны граффити, и не встречается в исконно египетских орнаментах. В основном они датируются ранними веками христианской эры.[5] хотя средневековое или даже современное (начало 20 века) происхождение нельзя исключить с уверенностью, поскольку рисунки не упоминаются в обширных списках граффити в храме, составленных Маргарет Мюррей в 1904 г.[6]
Подобные образцы иногда использовались в Англии как апотропные следы чтобы ведьмы не заходили в здания.[7] Освящение крестов точки в церквях, помазанных святой водой во время освящения церквей, также имеют форму перекрывающихся кругов.
В Исламское искусство, узор представляет собой одно из нескольких расположений кругов (другие используются для четырех- или пятислойных конструкций), используемых для построения сеток для Исламские геометрические узоры. Он используется для создания узоров с 6- и 12-конечными звездами, а также шестиугольниками в стиле, называемом гирих. Однако получающиеся в результате узоры обычно скрывают строительную сетку, представляя вместо этого дизайн переплетенной лямки.[8]
Европа
Образцы семи перекрывающихся кругов найдены на кипроархаической чаше I VIII-VII веков до н.э. на Кипре.[нужна цитата] и римские мозаики, например на Дворец ирода в 1 веке до нашей эры.
Рисунок изображен на одной из серебряных бляшек позднеримского клада. Kaiseraugst (открыт в 1961 г.).[9]Позже встречается как украшение в Готическая архитектура, а еще позже в Европе народное искусство раннего современного периода.
Примеры высокого средневековья включают Cosmati тротуары в Вестминстерское аббатство (13 век).[10]Леонардо да Винчи подробно обсуждались математические пропорции дизайна.[11]
Современное использование
Название «Цветок Жизни» современное, связано с Нью Эйдж движения, и обычно приписывается Друнвало Мелхиседеку в его книге Древняя тайна цветка жизни (1999).[12][13][14]
Узор и современное название получили широкое распространение в популярной культуре, моде, ювелирных изделиях, татуировках и декоративных изделиях. квилтинг был вызван бриллиантовое обручальное кольцо или же треугольное обручальное кольцо чтобы противопоставить это квадратный узор. Помимо редкого использования в моде,[15] он также используется в декоративном искусстве. Например, альбом Семпитерналь (2013) автор: Достань для меня горизонт использует Сетка 61 перекрывающихся кругов как главная особенность обложки альбома,[16] тогда как альбом Голова, полная мечтаний (2015) автор: Холодная игра В центре обложки альбома - сетка из 19 перекрывающихся кругов. Тизеры, иллюстрирующие обложку Голова, полная мечтаний широко отображались на Лондонское метро в последнюю неделю октября 2015 года.[17]
«Солнце Альп» (Итальянский Sole delle Alpi) символ использовался как эмблема Паданский национализм в северной Италии с 1990-х гг.[18] Он напоминает узор, который часто встречается в этой области на зданиях.[19]
Галерея
- Варианты шестиугольника с 1, 7 и 19 кругами
В приведенных ниже примерах узор имеет шестиугольный контур и дополнительно ограничен.
7-круг: Мозаичный пол из бани в Дворец ирода, I век до н.э.
- Похожие шаблоны
В примерах ниже узор не имеет шестиугольного контура.
Рисунок Леонардо да Винчи (Кодекс Атлантический, fol. 307в)
Чаша с мифологическими сценами, фризом со сфинксом и изображением царя, побеждающего своих врагов. Кипроархаический период I (VIII – VII вв. До н.э.). От Идалиона, Кипр.
Бал в руках имперского мужчины Лев-хранитель на Врата высшей гармонии, Запретный город, Пекин, Китай, показывая геометрический узор на своей поверхности.
Украшение пола из дворца короля северного Ирака Ашурбанипал, видимый в Лувре, датируется 645 годом до нашей эры.
Эмблема «Солнце Альп», используемая Lega Nord
Строительство
Марта Бартфельд, автор учебников по геометрическому искусству, описала свое независимое открытие дизайна в 1968 году. Ее первоначальное определение гласило: «Этот рисунок состоит из кругов с радиусом 1 [дюйм], где каждая точка пересечения служит новым центром .Дизайн можно расширять. до бесконечности в зависимости от того, сколько раз отмечены нечетные точки ".
Фигурку узора можно нарисовать ручка и компас, путем создания нескольких серий взаимосвязанных кругов одного диаметра, касающихся центра предыдущего круга. Второй круг центрируется в любой точке первого круга. Все следующие круги сосредоточены на пересечении двух других кругов.
Прогрессии
Узор может быть расширен наружу в виде концентрических шестиугольных колец кругов, как показано. В первом ряду показаны кольца кругов. Вторая строка показывает трехмерную интерпретацию набора п×п×п куб сфер, если смотреть с диагональной оси. В третьей строке показан узор, завершенный частичными круговыми дугами в наборе завершенных кругов.
Расширяющиеся наборы содержат 1, 7, 19, 37, 61, 91, 127 и т. Д. Кругов, а также продолжаются все более крупные шестиугольные кольца кругов. Количество кругов п3-(п-1)3 = 3п2-3п+1 = 3п(п-1)+1.
Эти перекрывающиеся круги также можно рассматривать как проекцию п-единица измерения куб сфер в трехмерном пространстве, если смотреть на диагональную ось. Сфер больше, чем кругов, потому что некоторые из них перекрываются в двух измерениях.
| 1-круг | 7-круг (8-1) | 19-круг (27-8) | 37-круг (64-27) | 61-круг (125-64) | 91-круг (216-125) | 127-круг ... (343-216) |
|---|---|---|---|---|---|---|
 | 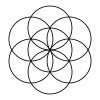 |  | 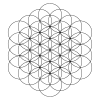 |  | 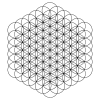 |  |
| 1-сфера (1×1×1) | 8-сфера (2×2×2) | 27-сфера (3×3×3) | 64-сфера (4×4×4) | 125-сфера (5×5×5) | 216-сфера (6×6×6) | 343-сфера (7×7×7) |
 |  |  | ||||
| +12 дуг | +24 дуги | +36 дуг | +48 дуг | +60 дуг | +72 дуги | +84 дуги |
 |  | 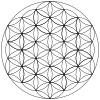 |  |  |  |
Другие варианты
Другой треугольная решетка форма обычна, с разделением круга как квадратный корень в 3 раза больше их радиуса. Ричард Кершнер показал в 1939 году, что нет расположение кругов может покрывать плоскость более эффективно, чем эта гексагональная решетка.[20]
Две смещенные копии этого кругового узора образуют ромбическая черепица узор, а три копии образуют исходный треугольный узор.
Две офсетные копии шаблона минимального закрывающего круга (слева) образуют ромбическая черепица узор, как эта красная, синяя версия.
Пример на Айюбид Ракка посуда стеклянная банка из керамики. Сирия, 12-13 века
Черное и белое мозаика тротуар на Вилла Адриана, Тиволи, II век нашей эры
Связанные понятия
Центр линза 2-круговой фигуры называется Vesica piscis, из Евклид. Два круга еще называют Круги Вильярсо как плоское пересечение тора. Области внутри одного круга и вне другого круга называются луна.
Фигура из трех кругов напоминает изображение борромео кольца и используется в 3 комплекта теория Диаграммы Венна. Его интерьер делает уникурсальный путь называется Triquetra. Центр фигуры из трех кругов называется треугольник Рило.
 Vesica piscis |  Кольца Борромео |  Диаграмма Венна |  Triquetra |  Треугольник Рело |
Немного сферические многогранники с краями вдоль большие круги могут быть стереографически спроецированы на плоскость в виде перекрывающихся кругов.
 октаэдр |  Кубооктаэдр | 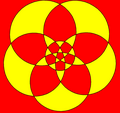 Икосододекаэдр |
Узор из 7 кругов также называют Исламский образец семи кругов для его использования в Исламское искусство.
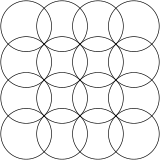
Квадратная сетка перекрывающихся кругов
| ||
|
В квадратная решетка форму можно увидеть с кругами, которые выстраиваются горизонтально и вертикально, пересекаясь по диагоналям. Рисунок выглядит немного иначе при повороте по диагонали, который также называется центрированная квадратная решетка формы, потому что ее можно рассматривать как две квадратные решетки, каждая из которых центрирована на зазорах другой.
Это называется Мотив кавунг на индонезийском батик, и находится на стенах индуистского храма 8-го века Прамбанан в Ява.
Это называется Апсамиккум из древних Месопотамский математика.[21]
Квадратную сетку можно увидеть на гранецентрированная кубическая решетка, с 12 сферами в контакте вокруг каждой сферы
Связанные сетка из пяти перекрывающихся кругов состоит из двух наборов перекрывающихся кругов с полусмещением.[22]
Смотрите также
- Равномерные мутации симметрии мозаики - мутации паттернов в трехмерном пространстве
- Теория узлов
Рекомендации
- ^ Исламское искусство и геометрический дизайн: упражнения для обучения
- ^ Лувр Инв. AO 19915.Жорж Перро, Шарль Чипье, История искусства в Халдее и Ассирии, т. 1, Лондон 1884, с. 240, (gutenberg.org)
- ^ Вайсштейн, Эрик В. «Цветок жизни». MathWorld.
- ^ Стюарт, Малкольм (2008). «« Цветок жизни »и Осирион - факты интереснее фантастики». Египетский тур (Дэвид Ферлонг). Получено 8 ноября, 2015.
- ^ Ферлонг, Дэвид. «Осирион и цветок жизни». Получено 8 ноября, 2015. Ферлонг утверждает, что эти гравюры могут датироваться не ранее 535 г. до н.э. и, вероятно, датируются II и IV веками нашей эры. Его исследования основаны на фотографических свидетельствах греческого текста, которые еще предстоит полностью расшифровать. Текст виден рядом с рисунками и в верхней части столбцов, высота которых превышает 4 метра. Ферлонг предполагает, что Осирион был наполовину заполнен песком до того, как были нарисованы круги, и, следовательно, вероятно, был намного позже конца Династия птолемеев.
- ^ Мюррей, Маргарет Элис (1904). Осирион в Абидосе Лондон. п. 35 год. Получено 4 ноября, 2015.
- ^ Кеннеди, Маев (31 октября 2016 г.). «Ведьминские следы: общественность просила поискать древние царапины на зданиях». Хранитель. Получено 31 октября, 2016.
- ^ Броуг, Эрик (2008). Исламские геометрические узоры. Темза и Гудзон. С. 22–23 и пасс. ISBN 978-0-500-28721-7.
- ^ Ганс Ульрих Инстински: Der spätrömische Silberschatzfund von Kaiseraugst. Майнц 1971, мемориальная доска 85.
- ^ Тротуары Космати в Вестминстерском аббатстве. Абгеруфен А.М. 14 сентября 2013 г.
- ^ Кодекс Атлантический, фол. 307r – 309v, 459r (датированы 1478-1519 гг.).
- ^ Бартфельд, Марта (2005). Как создавать мандалы сакральной геометрии. Санта-Фе, Нью-Мексико: Mandalart Creations. п. 35. ISBN 9780966228526. OCLC 70293628.
- ^ Вольфрам, Стивен (14 мая 2002 г.). Новый вид науки. Wolfram Media, Inc. стр.43 и 873–874. ISBN 1-57955-008-8.
- ^ Вайсштейн, Эрик В. (2002). CRC Краткая энциклопедия математики, второе издание. CRC Press. п. 1079. ISBN 1420035223.
- ^ Например. Заман, Сана (14 мая 2013 г.). «Заем Джамал представляет новую коллекцию на борту частной яхты в Дубай Марине». Haute Living. Получено 9 ноября, 2015.
- ^ Купер, Эд (25 февраля 2013 г.). «Bring Me The Horizon: этот альбом должен быть вечным». Независимый. Архивировано из оригинал 23 октября 2015 г.. Получено 8 ноября, 2015.
- ^ Денхэм, Джесс (6 ноября 2015 г.). "Новый альбом Coldplay: Бейонсе и Ноэль Галлахер появятся на A Head Full of Dreams". Независимый. Получено 8 ноября, 2015.
- ^ "Смысл символа Соле делле Альпи" (на итальянском). Lega Nord. Архивировано из оригинал 12 января 2014 г.. Получено 1 декабря, 2014.
- ^ Ивано Дорболо (6 июня 2010 г.). «Церковь Сан-Эгидио и символ Альпийского солнца». Storia di Confine - Валли ди Натисоне. Получено 9 ноября, 2015.
- ^ Сферические упаковки, решетки и группы, Джон Конвей, Нил Дж. А. Слоан, Глава 2, раздел 1.1, Покрытие пространства перекрывающимся кругом. С. 31-32. Рисунок 2.1 Покрытие плоскости кругами (б) Более эффективное или более тонкое покрытие в шестиугольной решетке. [1]
- ^ Математика Месопотамии 2100-1600 гг. До н.э .: Технические константы в бюрократии и образовании (Оксфордские издания клинописных текстов), Элеонора Робсон, Clarendon Press, 1999, ISBN 978-0198152460 [2] на books.google.com
- ^ Создание квадратной сетки из кругов
внешняя ссылка
- Вайсштейн, Эрик В. «Круг-круг пересечение». MathWorld.
- Цветок жизни статья из The Mystica
| Викискладе есть медиафайлы по теме Цветок Жизни. |
| Викискладе есть медиафайлы по теме Солнце Альп. |