WikiDer > Идеальная хеш-функция

Perfect hash function

Идеальная хеш-функция для четырех показанных имен

Минимальная идеальная хеш-функция для четырех показанных имен

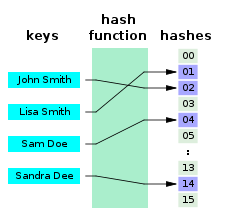
В Информатика, а идеальная хеш-функция для набора $S$ это хэш-функция который отображает различные элементы в $S$ к набору целых чисел, без столкновения. С математической точки зрения это инъективная функция.

Идеальные хеш-функции могут использоваться для реализации Справочная таблица с постоянным временем доступа наихудшего случая. Идеальная хеш-функция имеет много общего Приложения как и другие хэш-функции, но с тем преимуществом, что разрешение столкновения должен быть реализован. Кроме того, если ключи не являются данными, ключи не нужно хранить в таблице поиска, что экономит место.

Заявление

Идеальная хеш-функция со значениями в ограниченном диапазоне может использоваться для эффективных операций поиска, помещая ключи из $S$ (или другие связанные значения) в Справочная таблица проиндексировано выходом функции. Затем можно проверить, присутствует ли ключ в $S$ или найдите значение, связанное с этим ключом, по его ячейке в таблице. Каждый такой поиск занимает постоянное время в худший случай.^[1]

Строительство

Идеальная хеш-функция для определенного набора $S$ которые можно оценить за постоянное время и со значениями в небольшом диапазоне, можно найти с помощью рандомизированный алгоритм в количестве операций, пропорциональном размеру S. Исходная конструкция Фредман, Комлос и Семереди (1984) использует двухуровневую схему для отображения набора $S$ из $п$ элементы к ряду $О (п)$ индексы, а затем сопоставьте каждый индекс с диапазоном значений хеш-функции. Первый уровень их строительства выбирает большое число $п$ (больше, чем размер вселенная откуда $S$ нарисован), а параметр $k$ , и отображает каждый элемент $Икс$ из $S$ к индексу

{ displaystyle g (x) = (kx { bmod {p}}) { bmod {n}}.}

Если $k$ выбирается случайно, на этом шаге могут быть коллизии, но количество элементов $п я$ которые одновременно отображаются в один и тот же индекс $я$ вероятно, будет малым. Второй уровень их построения задает непересекающиеся диапазоны $О (п я 2)$ целые числа для каждого индекса $я$ . Он использует второй набор линейных модульных функций, по одной для каждого индекса. $я$ , чтобы сопоставить каждого члена $Икс$ из $S$ в диапазон, связанный с $грамм (Икс)$ .^[1]

В качестве Фредман, Комлос и Семереди (1984) показать, существует выбор параметра $k$ такая, что сумма длин диапазонов для $п$ разные значения $грамм (Икс)$ является $О (п)$ . Дополнительно для каждого значения $грамм (Икс)$ , существует линейная модулярная функция, отображающая соответствующее подмножество $S$ в диапазон, связанный с этим значением. Обе $k$ , а функции второго уровня для каждого значения $грамм (Икс)$ , можно найти в полиномиальное время путем случайного выбора значений, пока не будет найдено подходящее.^[1]

Сама хэш-функция требует места для хранения $О (п)$ хранить $k$ , $п$ , и все линейные модульные функции второго уровня. Вычисление хеш-значения заданного ключа $Икс$ может выполняться в постоянное время путем вычисления $грамм (Икс)$ , ища функцию второго уровня, связанную с $грамм (Икс)$ , и применяя эту функцию к $Икс$ .Модифицированная версия этой двухуровневой схемы с большим количеством значений на верхнем уровне может использоваться для построения идеальной хеш-функции, которая отображает $S$ в меньший диапазон длины $п + о (п)$ .^[1]

Нижние границы пространства

Использование $О (п)$ слова информации для хранения функции Фредман, Комлос и Семереди (1984) почти оптимален: любая идеальная хеш-функция, которую можно вычислить за постоянное время, требует, по крайней мере, количества битов, которое пропорционально размеру $S$ .^[2]

Расширения

Динамическое идеальное хеширование

Использование идеальной хеш-функции лучше всего в ситуациях, когда есть часто запрашиваемый большой набор, $S$ , который редко обновляется. Это потому, что любая модификация набора $S$ может привести к тому, что хеш-функция больше не будет идеальной для измененного набора. Решения, которые обновляют хэш-функцию каждый раз при изменении набора, известны как динамическое идеальное хеширование,^[3] но эти методы относительно сложно реализовать.

Минимальная идеальная хеш-функция

Минимальная идеальная хеш-функция - это идеальная хеш-функция, которая отображает $п$ ключи к $п$ последовательные целые числа - обычно числа из $0$ к $п - 1$ или из $1$ к $п$ . Более формальный способ выразить это: пусть $j$ и $k$ быть элементами некоторого конечного множества $S$ . потом $F$ является минимальной совершенной хеш-функцией тогда и только тогда, когда $F (j) = F (k)$ подразумевает $j = k$ (приемистость) и существует целое число $а$ такой, что диапазон $F$ является $а .. а + | S | - 1$ . Было доказано, что минимальная совершенная хеш-схема общего назначения требует не менее 1,44 бита на ключ.^[4] Наиболее известные в настоящее время схемы минимального идеального хеширования могут быть представлены с использованием менее 1,56 бит / ключ, если у них будет достаточно времени.^[5]

Сохранение заказа

Минимальная идеальная хеш-функция $F$ является сохранение порядка если ключи даны в каком-то порядке $а 1, а 2, ..., а п$ и для любых ключей $а j$ и $а k$ , $j < k$ подразумевает $F (а j) а k)$ .^[6] В этом случае значение функции - это просто позиция каждого ключа в отсортированном порядке всех ключей. Простая реализация сохраняющих порядок минимальных совершенных хэш-функций с постоянным временем доступа заключается в использовании (обычной) идеальной хеш-функции или кукушка для хранения таблицы поиска позиций каждого ключа. Если ключи, подлежащие хешированию, сами хранятся в отсортированном массиве, можно сохранить небольшое количество дополнительных битов на ключ в структуре данных, которая может использоваться для быстрого вычисления хеш-значений.^[7] Сохраняющие порядок минимальные совершенные хеш-функции обязательно требуют $Ω (п бревно п)$ биты, которые будут представлены.^[8]

Связанные конструкции

Простая альтернатива идеальному хешированию, которая также допускает динамические обновления, - это кукушка. Эта схема сопоставляет ключи с двумя или более местоположениями в пределах диапазона (в отличие от идеального хеширования, которое сопоставляет каждый ключ с одним местоположением), но делает это таким образом, что ключи могут быть назначены один к одному местоположениям, в которых они были нанесен на карту. Поиск по этой схеме выполняется медленнее, потому что необходимо проверять несколько местоположений, но, тем не менее, занимает постоянное время в худшем случае.^[9]

дальнейшее чтение

Ричард Дж. Чичелли. Минимальные идеальные хеш-функции стали проще, Сообщения ACM, Vol. 23, номер 1, январь 1980 г.
Томас Х. Кормен, Чарльз Э. Лейзерсон, Рональд Л. Ривест, и Клиффорд Штайн. Введение в алгоритмы, Третье издание. MIT Press, 2009. ISBN 978-0262033848. Раздел 11.5: Идеальное хеширование, стр. 267, 277–282.
Фабиано К. Ботельо, Расмус Паг и Нивио Зивиани. «Идеальное хеширование для приложений управления данными».
Фабиано К. Ботельо и Нивио Зивиани. «Внешнее идеальное хеширование для очень больших наборов ключей». 16-я конференция ACM по управлению информацией и знаниями (CIKM07), Лиссабон, Португалия, ноябрь 2007 г.
Джамал Белаццуги, Паоло Болди, Расмус Паг и Себастьяно Винья. «Монотонное минимальное идеальное хеширование: поиск в отсортированной таблице с O (1) обращениями». В материалах 20-го ежегодного симпозиума ACM-SIAM по дискретной математике (SODA), Нью-Йорк, 2009. ACM Press.
Дуглас С. Шмидт, GPERF: идеальный генератор хеш-функций, Отчет C ++, SIGS, Vol. 10, No. 10, ноябрь / декабрь 1998 г.

внешняя ссылка

gperf является Открытый исходный код Генератор идеального хэша C и C ++ (очень быстрый, но работает только для небольших наборов)
Минимальное идеальное хеширование (алгоритм Боба) Боб Дженкинс
cmph: C Minimal Perfect Hash Library, реализация с открытым исходным кодом для многих (минимальных) идеальных хешей (работает для больших наборов)
Sux4J: открытый исходный код монотонного минимального идеального хеширования в Java
MPHSharp: идеальные методы хеширования в C #
BBHash: минимальная идеальная хеш-функция в C ++ только для заголовков
Perfect :: Hash, идеальный генератор хешей на Perl, который делает код C. Имеет раздел "предшествующий уровень техники", на который стоит обратить внимание.

[inventor-1] а ^б ^c ^d Фредман, Майкл Л.; Комлош, Янош; Семереди, Эндре (1984), "Хранение разреженной таблицы с $О (1)$ Время доступа в наихудшем случае », Журнал ACM, 31 (3): 538, Дои:10.1145/828.1884, МИСТЕР 0819156

[2] Фредман, Майкл Л.; Комлош, Янош (1984), «О размере разделяющих систем и семейств совершенных хеш-функций», Журнал SIAM по алгебраическим и дискретным методам, 5 (1): 61–68, Дои:10.1137/0605009, МИСТЕР 0731857.

[3] Дицфельбингер, Мартин; Карлин, Анна; Мельхорн, Курт; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарджан, Роберт Э. (1994), «Динамическое идеальное хеширование: верхняя и нижняя границы», SIAM Журнал по вычислениям, 23 (4): 738–761, Дои:10.1137 / S0097539791194094, МИСТЕР 1283572.

[CHD-4] Белаззуги, Джамал; Botelho, Fabiano C .; Дицфельбингер, Мартин (2009), "Хешировать, перемещать и сжимать" (PDF), Алгоритмы - ESA 2009: 17-й ежегодный европейский симпозиум, Копенгаген, Дания, 7-9 сентября 2009 г., Материалы (PDF), Конспект лекций по информатике, 5757, Берлин: Springer, стр. 682–693, CiteSeerX 10.1.1.568.130, Дои:10.1007/978-3-642-04128-0_61, МИСТЕР 2557794.

[RecSplit-5] Эспозито, Эммануэль; Мюллер Граф, Томас; Винья, Себастьяно (2020), «RecSplit: минимальное идеальное хеширование с помощью рекурсивного разделения», 2020 Труды симпозиума по разработке алгоритмов и экспериментам (ALENEX), Труды, стр. 175–185, arXiv:1910.06416, Дои:10.1137/1.9781611976007.14.

[6] Дженкинс, Боб (14 апреля 2009 г.), «Минимальное совершенное хеширование с сохранением порядка», в Black, Paul E. (ed.), Словарь алгоритмов и структур данных, Национальный институт стандартов и технологий США, получено 2013-03-05

[7] Белаззуги, Джамал; Болди, Паоло; Паг, Расмус; Винья, Себастьяно (ноябрь 2008 г.), «Теория и практика монотонного минимального идеального хеширования», Журнал экспериментальной алгоритмики, 16, Изобразительное искусство. нет. 3.2, 26pp, Дои:10.1145/1963190.2025378.

[8] Фокс, Эдвард А .; Чен, Ци Фань; Daoud, Amjad M .; Хит, Ленвуд С. (июль 1991 г.), «Сохраняющие порядок минимальные совершенные хеш-функции и поиск информации» (PDF), ACM-транзакции в информационных системах, Нью-Йорк, Нью-Йорк, США: ACM, 9 (3): 281–308, Дои:10.1145/125187.125200.

[9] Паг, Расмус; Родлер, Флемминг Фрич (2004), «Кукушечка», Журнал алгоритмов, 51 (2): 122–144, Дои:10.1016 / j.jalgor.2003.12.002, МИСТЕР 2050140.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Navigation