WikiDer > Постоянная структура данных
В вычисление, а постоянная структура данных это структура данных который всегда сохраняет предыдущую версию при ее изменении. Такие структуры данных эффективно неизменный, поскольку их операции (явно) не обновляют структуру на месте, а вместо этого всегда создают новую обновленную структуру. Этот термин был введен в статье Дрисколла, Сарнака, Слеатора и Тарьянса 1986 года.[1]
Структура данных частично стойкий если доступны все версии, но можно изменить только самую новую версию. Структура данных полностью стойкий если каждая версия может быть доступна и изменена. Если есть также операция слияния или слияния, которая может создать новую версию из двух предыдущих версий, структура данных называется непрерывно стойкий. Структуры, которые не являются постоянными, называются эфемерный.[2]
Эти типы структур данных особенно распространены в логичный и функциональное программирование[2], поскольку языки в этих парадигмах препятствуют (или полностью запрещают) использование изменяемых данных.
Частичное или полное постоянство
В модели частичной сохраняемости программист может запросить любую предыдущую версию структуры данных, но может обновить только последнюю версию. Это означает линейный порядок среди каждой версии структуры данных.[3] В полностью персистентной модели и обновления, и запросы разрешены для любой версии структуры данных. В некоторых случаях рабочие характеристики запросов или обновления старых версий структуры данных может быть разрешено ухудшаться, как и в случае Структура данных веревки.[4] Кроме того, структура данных может называться конфлюентно постоянной, если, помимо того, что она полностью постоянна, две версии одной и той же структуры данных могут быть объединены для формирования новой версии, которая по-прежнему остается полностью постоянной.[5]
Способы сохранения предыдущих версий
Копирование при записи
Один из методов создания устойчивой структуры данных - использовать предоставленную платформой временную структуру данных, такую как массив для хранения данных в структуре данных и копирования всей этой структуры данных с помощью семантика копирования при записи для любых обновлений в структуре данных. Это неэффективный метод, потому что вся структура данных резервного копирования должна копироваться при каждой записи, что приводит к наихудшим характеристикам производительности O (n · m) для m модификаций массива размера n.[нужна цитата]
Жирный узел
Метод толстого узла состоит в том, чтобы записывать все изменения, внесенные в поля узлов в самих узлах, без удаления старых значений полей. Для этого требуется, чтобы узлы были произвольно «толстыми». Другими словами, каждый толстый узел содержит одинаковую информацию и указатель fields как эфемерный узел, а также пространство для произвольного числа дополнительных значений поля. Каждое дополнительное значение поля имеет связанное имя поля и отметку версии, которая указывает версию, в которой указанное поле было изменено, чтобы иметь указанное значение. Кроме того, каждый толстый узел имеет свой штамп версии, указывающий версию, в которой узел был создан. Единственная цель узлов, имеющих отметки версии, - убедиться, что каждый узел содержит только одно значение на имя поля для каждой версии. Для навигации по структуре каждое исходное значение поля в узле имеет отметку версии, равную нулю.
Сложность жирового узла
При использовании метода толстого узла для каждой модификации требуется O (1) места: просто сохраните новые данные. Каждая модификация занимает O (1) дополнительного времени для сохранения модификации в конце истории модификаций. Это амортизированное время связаны, предполагая, что история изменений хранится в расширяемом массив. В время доступа, правильная версия в каждом узле должна быть найдена по мере прохождения структуры. Если бы необходимо было сделать "m" модификаций, то каждая операция доступа имела бы замедление на O (log m) из-за затрат на поиск ближайшей модификации в массиве.
Копирование пути
При использовании метода копирования пути копируются все узлы на пути к любому узлу, который будет изменен. Эти изменения должны быть каскадный обратно через структуру данных: все узлы, указывающие на старый узел, должны быть изменены, чтобы вместо этого указывать на новый узел. Эти модификации вызывают новые каскадные изменения и так далее, пока не будет достигнут корневой узел.
Сложность копирования пути
При m модификациях это стоит O (log m) добавки. искать время. Время и пространство модификации ограничены размером самого длинного пути в структуре данных и стоимостью обновления в эфемерной структуре данных. В сбалансированном двоичном дереве поиска без родительских указателей сложность времени модификации наихудшего случая равна O (log n + стоимость обновления). Однако в связанном списке сложность времени модификации наихудшего случая составляет O (n + стоимость обновления).
Комбинация
Sleator, Tarjan и другие. подошел[нужна цитата] с возможностью комбинировать методы толстых узлов и копирования пути, достигая O (1) замедления доступа и O (1) пространственной и временной сложности модификации.
В каждом узле хранится одно поле модификации. Это поле может содержать одну модификацию узла - либо модификацию одного из указателей, либо ключа узла, либо некоторой другой части специфичных для узла данных - и отметку времени, когда была применена эта модификация. Изначально поле модификации каждого узла пусто.
Каждый раз, когда к узлу обращаются, флажок модификации ставится, и его временная метка сравнивается со временем доступа. (Время доступа определяет версию рассматриваемой структуры данных.) Если поле модификации пусто или время доступа предшествует времени модификации, то поле модификации игнорируется и рассматривается только нормальная часть узла. С другой стороны, если время доступа превышает время модификации, то используется значение в поле модификации, переопределяя это значение в узле.
Изменение узла работает следующим образом. (Предполагается, что каждая модификация касается одного указателя или подобного поля.) Если поле модификации узла пусто, то оно заполняется модификацией. В противном случае поле модификации заполнено. Создается копия узла, но с использованием только последних значений. Модификация выполняется непосредственно на новом узле, без использования окна модификации. (Одно из полей нового узла перезаписывается, а поле его модификации остается пустым.) Наконец, это изменение каскадно передается родительскому узлу, как при копировании пути. (Это может включать в себя заполнение поля модификации родителя или рекурсивное создание копии родителя. Если у узла нет родителя - это корень, - новый корень добавляется к отсортированный массив корней.)
С этим алгоритмв любой момент времени t в структуре данных существует не более одного блока модификации со временем t. Таким образом, модификация во время t разбивает дерево на три части: одна часть содержит данные до момента t, другая часть содержит данные после времени t, а одна часть не была затронута модификацией.
Сложность комбинации
Время и место для модификаций требуют амортизированного анализа. Для модификации требуется O (1) амортизированного пространства и O (1) амортизированного времени. Чтобы понять почему, используйте потенциальная функция ϕ, где ϕ (T) - количество полных активных узлов в T. Активные узлы T - это просто узлы, доступные из текущего корня в текущее время (то есть после последней модификации). Полные активные узлы - это активные узлы, чьи поля модификации заполнены.
Каждая модификация включает в себя некоторое количество копий, скажем k, за которым следует одно изменение в поле модификации. Рассмотрим каждую из k копий. Каждый требует O (1) пространства и времени, но уменьшает потенциальную функцию на единицу. (Во-первых, копируемый узел должен быть полным и активным, чтобы он вносил свой вклад в потенциальную функцию. Однако потенциальная функция будет отключена только в том случае, если старый узел недоступен в новом дереве. Но известно, что он недоступен в новом дереве - следующим шагом в алгоритме будет изменение родительского узла, чтобы он указывал на копию. Наконец, известно, что поле модификации копии пусто. Таким образом, заменен полный рабочий узел заменяется пустым живым узлом, и ϕ уменьшается на единицу.) Последний шаг заполняет поле модификации, которое стоит O (1) времени и увеличивает ϕ на единицу.
Суммируя все вместе, изменение ϕ равно ∆ϕ = 1− k. Таким образом, алгоритм занимает O (k + Δϕ) = O (1) пространства и O (k + Δϕ +1) = O (1) раз
Примеры постоянных структур данных
Возможно, самая простая постоянная структура данных - это односвязный список или минусысписок, простой список объектов, каждый из которых содержит Справка к следующему в списке. Это настойчиво, потому что хвостик из списка можно взять, имея в виду последний k предметы для некоторых k, и перед ним могут быть добавлены новые узлы. Хвост не будет дублироваться, вместо этого он станет общим для старого и нового списков. Пока содержимое хвоста неизменяемо, это совместное использование будет невидимым для программы.
Многие распространенные структуры данных на основе ссылок, такие как красно-черные деревья,[6] стеки,[7] и Treaps,[8] может быть легко адаптирован для создания постоянной версии. Некоторым другим нужно немного больше усилий, например: очереди, выводит из очереди, и расширения, включая min-deques (которые имеют дополнительный О(1) операция мин возвращая минимальный элемент) и деки произвольного доступа (которые имеют дополнительную операцию произвольного доступа с сублинейной, чаще всего логарифмической, сложностью).
Также существуют постоянные структуры данных, использующие деструктивные[требуется разъяснение] операции, что делает невозможным их эффективную реализацию на чисто функциональных языках (например, Haskell вне специализированных монад, таких как состояние или ввод-вывод), но возможно на таких языках, как C или Java. Этих типов структур данных часто можно избежать с помощью другого дизайна. Одним из основных преимуществ использования чисто постоянных структур данных является то, что они часто лучше работают в многопоточных средах.
Связанные списки
По отдельности связанные списки представляют собой простую структуру данных в функциональных языках.[9] Немного ML-производные языки, например Haskell, являются чисто функциональными, потому что после того, как узел в списке был выделен, он не может быть изменен, только скопирован, указан или уничтожен уборщик мусора когда к нему ничего не относится. (Обратите внимание, что сам ML является не чисто функциональный, но поддерживает подмножество неразрушающих операций со списком, что также верно в Лисп (LISt Processing) диалекты функционального языка, такие как Схема и Ракетка.)
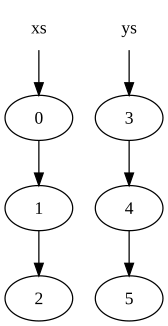
Рассмотрим два списка:
xs = [0, 1, 2] ys = [3, 4, 5]
Они будут представлены в памяти следующим образом:
где кружок обозначает узел в списке (стрелка вниз представляет второй элемент узла, который является указателем на другой узел).
Теперь объединим два списка:
zs = xs ++ ys
приводит к следующей структуре памяти:
Обратите внимание, что узлы в списке хз были скопированы, но узлы в ys общие. В результате исходные списки (хз и ys) сохраняются и не были изменены.
Причина копирования в том, что последний узел в хз (узел, содержащий исходное значение 2) нельзя изменить так, чтобы он указывал на начало ys, потому что это изменит значение хз.
Деревья
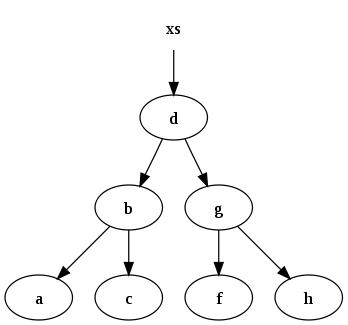
Рассмотрим двоичное дерево поиска,[9] где каждый узел в дереве имеет рекурсивный инвариантный что все подузлы, содержащиеся в левом поддереве, имеют значение, которое меньше или равно значению, хранящемуся в узле, а подузлы, содержащиеся в правом поддереве, имеют значение, которое больше значения, хранящегося в узле.
Например, набор данных
xs = [a, b, c, d, f, g, h]
может быть представлено следующим двоичным деревом поиска:
Функция, которая вставляет данные в двоичное дерево и поддерживает инвариант:
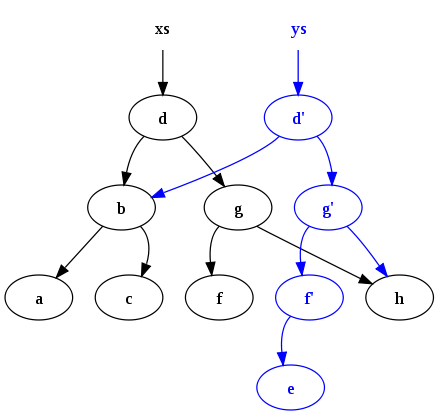
весело вставить (Икс, E) = Т (E, Икс, E) | вставить (Икс, s так как Т (а, у, б)) = если Икс < у тогда Т (вставить (Икс, а), у, б) еще если Икс > у тогда Т (а, у, вставить (Икс, б)) еще sПосле выполнения
ys = insert ("e", xs)Производится следующая конфигурация:
Обратите внимание на два момента: во-первых, исходное дерево (хз) сохраняется. Во-вторых, старое и новое дерево используют общие узлы. С такой настойчивостью и общением трудно обойтись без какой-либо формы вывоз мусора (GC) для автоматического освобождения узлов, которые не имеют живых ссылок, и именно поэтому GC - это функция, обычно встречающаяся в функциональные языки программирования.
Постоянный хэш-массив сопоставленного дерева
Отображенное дерево постоянного хеш-массива является специализированным вариантом хэш-массив сопоставленного дерева который сохранит предыдущие версии при любых обновлениях. Он часто используется для реализации постоянной структуры данных карты общего назначения.[10]
Попытки сопоставления хэш-массива были первоначально описаны в статье 2001 г. Фил Бэгвелл под названием «Идеальные хеш-деревья». В этой статье представлен изменчивый Хеш-таблица где «Время вставки, поиска и удаления является небольшим и постоянным, независимо от размера набора ключей, операции - O (1). Малое время наихудшего случая для операций вставки, поиска и удаления может быть гарантировано, а пропуски стоят меньше, чем успешный поиск».[11] Затем эта структура данных была изменена Рич Хикки быть полностью настойчивым для использования в Clojure язык программирования.[12]
Концептуально попытки сопоставления хэш-массива работают аналогично любому универсальному дерево в том, что они хранят узлы иерархически и извлекают их, следуя пути вниз к конкретному элементу. Ключевое отличие состоит в том, что попытки сопоставления хэш-массива сначала используют хэш-функция чтобы преобразовать свой ключ поиска в целое число (обычно 32- или 64-разрядное). Затем путь вниз по дереву определяется путем использования срезов двоичного представления этого целого числа для индексации в разреженный массив на каждом уровне дерева. Листовые узлы дерева ведут себя так же, как ведра, используемые для построения хеш-таблицы и может содержать или не содержать несколько кандидатов в зависимости от хеш-коллизии.[10]
В большинстве реализаций попыток сопоставления постоянного хеш-массива используется коэффициент ветвления 32. Это означает, что на практике, в то время как вставки, удаления и поиск в постоянном массиве хешей, отображенном trie, имеют вычислительную сложность О(журнал п), для большинства приложений они фактически представляют собой постоянное время, так как потребуется чрезвычайно большое количество записей, чтобы любая операция занимала более десятка шагов.[13]
Использование в языках программирования
Haskell
Haskell - это чистый функциональный язык и поэтому не допускает мутации. Следовательно, все структуры данных на языке являются постоянными, поскольку невозможно не сохранить предыдущее состояние структуры данных с функциональной семантикой.[14] Это связано с тем, что любое изменение структуры данных, которое сделало бы предыдущие версии структуры данных недействительными, нарушило бы ссылочная прозрачность.
В стандартной библиотеке Haskell есть эффективные постоянные реализации связанных списков,[15] Карты (реализованные как деревья со сбалансированным размером),[16] и наборы[17] среди прочего.[18]
Clojure
Как и многие языки программирования в Лисп семейства Clojure содержит реализацию связанного списка, но, в отличие от других диалектов, его реализация связного списка обеспечивает постоянство, а не постоянство по соглашению.[19] Clojure также имеет синтаксические литералы для эффективных реализаций постоянных векторов, карт и наборов, основанных на попытках сопоставления постоянного хэш-массива. Эти структуры данных реализуют обязательные только для чтения части Фреймворк коллекций Java.[20]
Разработчики языка Clojure рекомендуют использовать постоянные структуры данных вместо изменяемых структур данных, потому что они имеют семантика значений что дает то преимущество, что позволяет свободно обмениваться ими между потоками с дешевыми псевдонимами, легко создавать и не зависит от языка.[21]
Эти структуры данных составляют основу поддержки Clojure для параллельные вычисления поскольку они позволяют легко повторить операции, чтобы обойти гонки данных и атомный сравнить и поменять местами семантика.[22]
Вяз
В Язык программирования Elm является чисто функциональным, как Haskell, что делает все его структуры данных постоянными по необходимости. Он содержит постоянные реализации связанных списков, а также постоянные массивы, словари и наборы.[23]
Вяз использует обычай виртуальный DOM реализация, которая использует постоянный характер данных Elm. В 2016 году разработчики Elm сообщили, что этот виртуальный DOM позволяет языку Elm отображать HTML быстрее, чем популярный JavaScript рамки Реагировать, Ember, и Угловой.[24]
JavaScript
Популярная внешняя среда JavaScript Реагировать часто используется вместе с системой государственного управления, которая реализует Архитектура потока,[25][26] популярной реализацией которой является библиотека JavaScript Redux. Библиотека Redux основана на шаблоне управления состоянием, используемом в языке программирования Elm, что означает, что она требует, чтобы пользователи обрабатывали все данные как постоянные.[27] В результате проект Redux рекомендует, чтобы в определенных случаях пользователи использовали библиотеки для принудительных и эффективных постоянных структур данных. Сообщается, что это обеспечивает более высокую производительность, чем при сравнении или создании копий обычных объектов JavaScript.[28]
Одна из таких библиотек постоянных структур данных Immutable.js основана на структурах данных, сделанных доступными и популяризованными Clojure и Scala.[29] В документации Redux он упоминается как одна из возможных библиотек, которые могут обеспечить принудительную неизменяемость.[28] Mori.js привносит в JavaScript структуры данных, подобные тем, что есть в Clojure. [30]. Immer.js предлагает интересный подход, при котором «создается следующее неизменяемое состояние путем изменения текущего». [31]
Scala
Язык программирования Scala способствует использованию постоянных структур данных для реализации программ с использованием «объектно-функционального стиля».[32] Scala содержит реализации многих постоянных структур данных, включая связанные списки, Красно-черные деревья, а также попытки сопоставления постоянного хеш-массива, представленные в Clojure.[33]
Вывоз мусора
Поскольку постоянные структуры данных часто реализуются таким образом, что последовательные версии структуры данных совместно используют базовую память.[34] эргономичное использование таких структур данных обычно требует некоторой формы автоматический сбор мусора система, такая как подсчет ссылок или отметить и подметать.[35] На некоторых платформах, где используются постоянные структуры данных, есть возможность не использовать сборку мусора, что при этом может привести к утечки памяти, в некоторых случаях может положительно повлиять на общую производительность приложения.[36]
Смотрите также
- Копирование при записи
- Навигационная база данных
- Постоянные данные
- Ретроактивные структуры данных
- Чисто функциональная структура данных
использованная литература
- ^ Дрисколл Дж. Р., Сарнак Н., Слеатор Д. Д., Тарьян Р. Э. (1986). Обеспечение постоянства структур данных. Судебный процесс STOC '86. Материалы восемнадцатого ежегодного симпозиума ACM по теории вычислений. С. 109–121. CiteSeerX 10.1.1.133.4630. Дои:10.1145/12130.12142. ISBN 978-0-89791-193-1.
- ^ а б Каплан, Хаим (2001). «Постоянные структуры данных». Справочник по структурам данных и приложениям.
- ^ Кончон, Сильвен; Филлиатр, Жан-Кристоф (2008), «Полупостоянные структуры данных», Языки и системы программирования, Конспект лекций по информатике, 4960, Springer Berlin Heidelberg, стр. 322–336, Дои:10.1007/978-3-540-78739-6_25, ISBN 9783540787389
- ^ Тиарк, Багвелл, Филип Ромпф (2011). RRB-деревья: эффективные неизменяемые векторы. OCLC 820379112.
- ^ Бродал, Герт Стёльтинг; Макрис, Христос; Цичлас, Костас (2006), "Чисто функциональные отсортированные списки с постоянным временем наихудшего случая, подключаемые к сети", Конспект лекций по информатике, Springer Berlin Heidelberg, стр. 172–183, CiteSeerX 10.1.1.70.1493, Дои:10.1007/11841036_18, ISBN 9783540388753
- ^ Нил Сарнак; Роберт Э. Тарджан (1986). «Расположение плоских точек с использованием постоянных деревьев поиска» (PDF). Коммуникации ACM. 29 (7): 669–679. Дои:10.1145/6138.6151. Архивировано из оригинал (PDF) на 2015-10-10. Получено 2011-04-06.
- ^ Крис Окасаки. «Чисто функциональные структуры данных (тезис)» (PDF). Цитировать журнал требует
| журнал =(Помогите) - ^ Лильензин, Олле (2013). «Конфлуентно постоянные множества и карты». arXiv:1301.3388. Bibcode:2013arXiv1301.3388L. Цитировать журнал требует
| журнал =(Помогите) - ^ а б Этот пример взят из Окасаки. См. Библиографию.
- ^ а б BoostCon (13.06.2017), C ++ Now 2017: Фил Нэш «Святой Грааль !? Постоянное Trie-хранилище с отображением хэш-массива для C ++», получено 2018-10-22
- ^ Фил, Багвелл (2001). «Идеальные хеш-деревья». Цитировать журнал требует
| журнал =(Помогите) - ^ "Мы уже на месте?". InfoQ. Получено 2018-10-22.
- ^ Steindorfer, Майкл Дж .; Винью, Юрген Дж. (2015-10-23). «Оптимизация попыток сопоставления хэш-массива для быстрых и компактных неизменяемых коллекций JVM». Уведомления ACM SIGPLAN. 50 (10): 783–800. Дои:10.1145/2814270.2814312. ISSN 0362-1340.
- ^ "Язык Haskell". www.haskell.org. Получено 2018-10-22.
- ^ "Data.List". hackage.haskell.org. Получено 2018-10-23.
- ^ "Data.Map.Strict". hackage.haskell.org. Получено 2018-10-23.
- ^ "Data.Set". hackage.haskell.org. Получено 2018-10-23.
- ^ "Производительность / Массивы - HaskellWiki". wiki.haskell.org. Получено 2018-10-23.
- ^ "Clojure - Отличия от других Lisp". clojure.org. Получено 2018-10-23.
- ^ "Clojure - структуры данных". clojure.org. Получено 2018-10-23.
- ^ «Основной доклад: ценность ценностей». InfoQ. Получено 2018-10-23.
- ^ "Clojure - Атомы". clojure.org. Получено 2018-11-30.
- ^ "ядро 1.0.0". package.elm-lang.org. Получено 2018-10-23.
- ^ "blog / blazing-fast-html-round-two". elm-lang.org. Получено 2018-10-23.
- ^ «Flux | Архитектура приложений для создания пользовательских интерфейсов». facebook.github.io. Получено 2018-10-23.
- ^ Мора, Осмель (18.07.2016). «Как управлять состоянием в React». Экосистема React. Получено 2018-10-23.
- ^ "Прочтите меня - Redux". redux.js.org. Получено 2018-10-23.
- ^ а б «Неизменяемые данные - Redux». redux.js.org. Получено 2018-10-23.
- ^ "Immutable.js". facebook.github.io. Архивировано из оригинал на 2015-08-09. Получено 2018-10-23.
- ^ https://swannodette.github.io/mori/
- ^ https://github.com/immerjs/immer
- ^ «Суть объектно-функционального программирования и практический потенциал Scala - блог codecentric AG». блог codecentric AG. 2015-08-31. Получено 2018-10-23.
- ^ ClojureTV (07.01.2013), Исключительная изобретательность: функциональные структуры данных в Scala - Даниэль Спивак, получено 2018-10-23
- ^ «Владимир Костюков - Записи / Слайды». kostyukov.net. Получено 2018-11-30.
- ^ "http://wiki.c2.com/?ImmutableObjectsAndGarbageCollection". wiki.c2.com. Получено 2018-11-30. Внешняя ссылка в
| название =(Помогите) - ^ «Последний рубеж в производительности Java: удаление сборщика мусора». InfoQ. Получено 2018-11-30.