WikiDer > Веревка (структура данных)
В компьютерное программирование, а веревка, или же шнур, это структура данных состоит из меньших струны который используется для эффективного хранения очень длинной строки и управления ею. Например, редактирование текста Программа может использовать веревку для представления редактируемого текста, чтобы такие операции, как вставка, удаление и произвольный доступ, могли выполняться эффективно.[1]
Описание
Веревка - это двоичное дерево где каждый лист (конечный узел) содержит строку и длину (также известную как «вес»), а каждый узел дальше вверх по дереву содержит сумму длин всех листьев слева от него. поддерево. Таким образом, узел с двумя дочерними элементами делит всю строку на две части: левое поддерево хранит первую часть строки, правое поддерево хранит вторую часть строки, а вес узла - это длина первой части.
Для веревочных операций предполагается, что строки, хранящиеся в узлах, являются постоянными. неизменяемые объекты в типичном неразрушающем случае с учетом некоторых копирование при записи поведение. Листовые узлы обычно реализуются как основные струны фиксированной длины с счетчик ссылок прикреплен для освобождения, когда больше не нужен, хотя другие вывоз мусора методы также могут быть использованы.
Операции
В следующих определениях N длина веревки.
Вставлять
- Определение:
Вставить (i, S ’): вставить строку S ’ начиная с позиции я в строке s, чтобы сформировать новую строку C1, …, Cя, S ', Cя + 1, …, Cм. - Временная сложность: .
Эту операцию можно выполнить с помощью Расколоть() и два Concat () операции. Стоимость - это сумма трех.
Индекс
- Определение:
Индекс (i): вернуть символ в позиции я - Временная сложность:
Чтобы получить я-й символ, мы начинаем рекурсивный поиск из корневого узла:
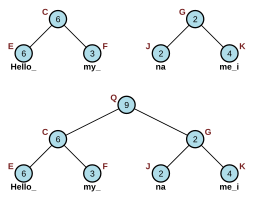
функция индекс(RopeNode узел, целое число я) если узел.масса <= я и существуют(узел.верно) тогда возвращаться индекс(узел.верно, я - узел.масса) конец если существуют(узел.оставили) тогда возвращаться индекс(узел.оставили, я) конец возвращаться узел.нить[я]конецНапример, чтобы найти символ в я = 10 на рисунке 2.1, показанном справа, начните с корневого узла (A), обнаружите, что 22 больше 10 и есть левый дочерний элемент, поэтому перейдите к левому дочернему узлу (B). 9 меньше 10, поэтому вычтите 9 из 10 (оставив я = 1) и подойдите к правому ребенку (D). Затем, поскольку 6 больше 1 и есть левый ребенок, перейдите к левому ребенку (G). 2 больше 1, и есть левый ребенок, поэтому снова перейдите к левому ребенку (J). Наконец, 2 больше 1, но нет левого дочернего элемента, поэтому ответом является символ с индексом 1 в короткой строке «na».
Concat
- Определение:
Конкат (S1, S2): соединить две веревки, S1 и S2, в одну веревку. - Временная сложность: (или же время для вычисления веса корня)
Конкатенацию можно выполнить, просто создав новый корневой узел с left = S1 и вправо = S2, что является постоянным временем. Вес родительского узла устанавливается равным длине левого дочернего узла. S1, который займет время, если дерево сбалансировано.
Поскольку для большинства операций с канатами требуются сбалансированные деревья, может потребоваться повторная балансировка дерева после объединения.
Расколоть
- Определение:
Разделить (i, S): разделить строку S на две новые струны S1 и S2, S1 = C1, …, Cя и S2 = Cя + 1, …, Cм. - Временная сложность:
Необходимо рассмотреть два случая:
- Точка разделения находится в конце строки (т.е. после последнего символа листового узла)
- Точка разделения находится в середине строки.
Второй случай сводится к первому путем разделения строки в точке разделения для создания двух новых листовых узлов, а затем создания нового узла, который является родительским для двух компонентных строк.
Например, чтобы разделить веревку из 22 символов, изображенную на рисунке 2.3, на две равные составные веревки длиной 11, запросите 12-й символ, чтобы найти узел. K на нижнем уровне. Удалить связь между K и грамм. Перейти к родительскому элементу грамм и вычтите вес K от веса D. Поднимитесь по дереву и удалите все правые ссылки на поддеревья, покрывающие символы после позиции 11, вычитая вес K от их родительских узлов (только узел D и А, в этом случае). Наконец, создайте осиротевшие узлы. K и ЧАС объединив их вместе и создав нового родителя п с весом равным длине левого узла K.
Поскольку для большинства операций с канатом требуются сбалансированные деревья, может потребоваться повторная балансировка дерева после разделения.
Удалить
- Определение:
Удалить (i, j): удалить подстроку Cя, …, Cя + j − 1, из s сформировать новую строку C1, …, Cя − 1, Cя + j, …, Cм. - Временная сложность: .
Эта операция может быть выполнена двумя Расколоть() и один Concat () операция. Сначала разделите веревку на три части, разделив их на я-й и я + j-й символ соответственно, который извлекает строку для удаления в отдельный узел. Затем соедините два других узла.
Отчет
- Определение:
Отчет (i, j): вывести строку Cя, …, Cя + j − 1. - Временная сложность:
Чтобы сообщить о строке Cя, …, Cя + j − 1, найдите узел ты который содержит Cя и вес (u)> = j, а затем пройти Т начиная с узла ты. Выход Cя, …, Cя + j − 1 делая обход по порядку из Т начиная с узла ты.
Сравнение с монолитными массивами
| Операция | Веревка | Нить |
|---|---|---|
| Индекс[1] | O (журнал n) | О (1) |
| Расколоть[1] | O (журнал n) | О (1) |
| Concatenate (разрушительный) | O (log n) без перебалансировки / O (n) худший случай | На) |
| Concatenate (неразрушающий) | На) | На) |
| Перебрать каждый символ[1] | На) | На) |
| Вставлять[2] | O (log n) без перебалансировки / O (n) худший случай | На) |
| Добавить[2] | O (log n) без перебалансировки / O (n) худший случай | O (1) амортизировано, O (n) худший случай |
| Удалить | O (журнал n) | На) |
| Отчет | O (j + журнал n) | O (j) |
| Строить | На) | На) |
Преимущества:
- Веревки позволяют намного быстрее вставлять и удалять текст, чем монолитные строковые массивы, операции над которыми имеют временную сложность O (n).
- При работе с веревками не требуется O (n) дополнительной памяти (массивы нуждаются в ней для операций копирования).
- Веревки не требуют больших непрерывных пространств памяти.
- Если используются только неразрушающие варианты операций, веревка является постоянная структура данных. В примере программы редактирования текста это приводит к простой поддержке нескольких отменить уровни.
Недостатки:
- Большее общее использование пространства, когда он не используется, в основном для хранения родительских узлов. Существует компромисс между тем, какая часть общей памяти является такими накладными расходами, и продолжительностью обработки фрагментов данных в виде строк. Строки на приведенных выше примерах нереально короткие для современных архитектур. Накладные расходы всегда равны O (n), но константу можно сделать сколь угодно малой.
- Увеличение времени для управления дополнительным хранилищем
- Повышенная сложность исходного кода; больший риск ошибок
В этой таблице сравнивается алгоритмический черты реализации струн и веревок, а не их сырая скорость. Строки на основе массивов имеют меньшие накладные расходы, поэтому (например) операции конкатенации и разделения выполняются быстрее для небольших наборов данных. Однако, когда строки на основе массива используются для более длинных строк, временная сложность и использование памяти для вставки и удаления символов становится неприемлемо большим. Напротив, веревочная структура данных имеет стабильную производительность независимо от размера данных. Кроме того, сложность пространства для веревок и массивов равна O (n). Таким образом, связки предпочтительнее, когда данные большие и часто изменяются.
Смотрите также
- В Кедр среда программирования, в которой верёвки использовались «почти с самого начала»[1]
- В Модель Т анфилада, аналогичная структура данных с начала 1970-х годов.
- Промежуточный буфер, структура данных, обычно используемая в текстовых редакторах, которая позволяет выполнять эффективные операции вставки и удаления, сгруппированные в одном месте.
- Штучный стол, другая структура данных, обычно используемая в текстовых редакторах
Рекомендации
Эта статья в значительной степени или полностью полагается на один источник. (Сентябрь 2011 г.) |
- ^ а б c d е Boehm, Hans-J; Аткинсон, Расс; Пласс, Майкл (декабрь 1995 г.). «Канаты: альтернатива струнам» (PDF). Программное обеспечение - практика и опыт. Нью-Йорк, Нью-Йорк, США: John Wiley & Sons, Inc. 25 (12): 1315–1330. Дои:10.1002 / spe.4380251203. В архиве из оригинала от 08.03.2020.
- ^ а б «Обзор реализации каната». www.sgi.com. Получено 2017-03-01.
внешняя ссылка
| Викискладе есть медиафайлы по теме Веревка (структура данных). |
- Реализация веревок "C cords" в библиотеке Boehm Garbage Collector.
- Спецификация SGI C ++ для веревок (поддерживается STLPort и libstdc ++)
- Веревки за C #
- веревки за Common Lisp
- Веревки для Явы
- Веревки для JavaScript
- Веревки за Лимбо
- веревки за Ним
- Веревки за OCaml
- пиропы за Python
- Веревки за Болтовня
- "Веревка" за Ржавчина