WikiDer > Строительство Томпсона - Википедия
В Информатика, Конструкция Томпсона алгоритм, также называемый алгоритмом Макнотона-Ямады-Томпсона[1], это метод преобразования регулярное выражение в эквивалент недетерминированный конечный автомат (NFA).[2] Этот NFA можно использовать для строки соответствия против регулярного выражения. Этому алгоритму приписывают Кен Томпсон.
Регулярные выражения и недетерминированные конечные автоматы - два представления формальные языки. Например, обработка текста Утилиты используют регулярные выражения для описания расширенных шаблонов поиска, но NFA лучше подходят для выполнения на компьютере. Следовательно, этот алгоритм представляет практический интерес, так как он может компилировать регулярные выражения в NFA. С теоретической точки зрения этот алгоритм является частью доказательства того, что они оба принимают одни и те же языки, то есть обычные языки.
NFA можно сделать детерминированной конструкция электростанции а затем быть минимизированный чтобы получить оптимальный автомат, соответствующий заданному регулярному выражению. Однако NFA также может быть интерпретируется напрямую.
Чтобы решить, описывают ли два заданных регулярных выражения один и тот же язык, каждое из них можно преобразовать в эквивалентный минимальный детерминированный конечный автомат через конструкцию Томпсона, конструкция электростанции, и Минимизация DFA. Если и только если полученные автоматы соглашаются вплоть до переименование состояний, языки регулярных выражений согласны.
Алгоритм
Алгоритм работает рекурсивно путем разделения выражения на составляющие подвыражения, из которых NFA будет построена с использованием набора правил.[3] Точнее из регулярного выражения E, полученный автомат А с функцией перехода δ уважает следующие свойства:
- А имеет ровно одно начальное состояние q0, который недоступен из любого другого состояния. То есть для любого состояния q и любое письмо а, не содержит q0.
- А имеет ровно одно конечное состояние qж, который недоступен из любого другого штата. То есть на любую букву а, .
- Позволять c быть числом конкатенации регулярного выражения E и разреши s быть количеством символов без скобок, т. е. |, *, а и ε. Тогда количество состояний А является 2s − c (линейная по размеру E).
- Количество переходов, выходящих из любого состояния, не превышает двух.
- Поскольку NFA м государства и самое большее е переходы из каждого состояния могут соответствовать строке длины п во время О(emn), NFA Томпсона может выполнять сопоставление с образцом за линейное время, предполагая, что алфавит фиксированного размера.[4][нужен лучший источник]
Правила
Следующие правила изображены согласно Aho et al. (2007),[1] п. 122. Далее N(s) и N(т) - НКА подвыражений s и т, соответственно.
В пустое выражение ε преобразуется в
А символ а входного алфавита преобразуется в
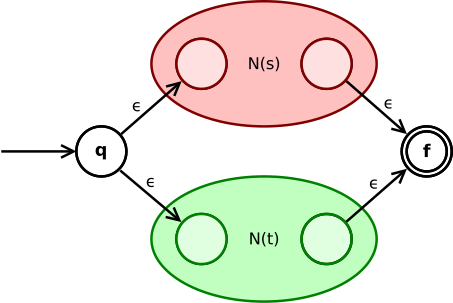
В выражение союза s|т конвертируется в
Состояние q переходит через ε либо в начальное состояние N(s) или же N(т). Их конечные состояния становятся промежуточными состояниями всего NFA и сливаются посредством двух ε-переходов в конечное состояние NFA.
В выражение конкатенации ул конвертируется в
Исходное состояние N(s) - начальное состояние всей NFA. Окончательное состояние N(s) становится начальным состоянием N(т). Окончательное состояние N(т) является конечным состоянием всей NFA.
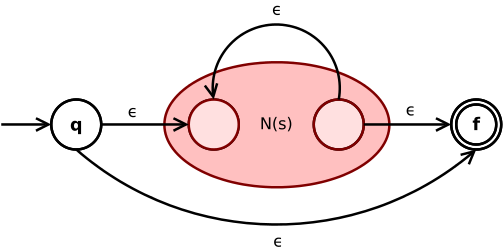
В Клини звезда выражение s* конвертируется в
Ε-переход связывает начальное и конечное состояние NFA с суб-NFA. N(s) между. Еще один ε-переход от внутреннего конечного к внутреннему начальному состоянию N(s) позволяет повторять выражение s по словам звездного оператора.
- В выражение в скобках (s) преобразуется в N(s) сам.
С этими правилами, используя пустое выражение и символ правила как базовые случаи, можно доказать с помощью математическая индукция что любое регулярное выражение может быть преобразовано в эквивалентную NFA.[1]
Пример
Приведены два примера: небольшой, неформальный, с результатом, и большой, с пошаговым применением алгоритма.
Маленький пример
На рисунке ниже показан результат построения Томпсона на (ε | a * b). Розовый овал соответствует а, бирюзовый овал соответствует а *зеленый овал соответствует боранжевый овал соответствует а * б, а синий овал соответствует ε.
Применение алгоритма
В качестве примера на картинке показан результат алгоритма построения Томпсона на регулярном выражении (0|(1(01*(00)*0)*1)*)* который обозначает набор двоичных чисел, кратных 3:
- {ε, «0», «00», «11», «000», «011», «110», «0000», «0011», «0110», «1001», «1100», «1111» , "00000", ...}.
Верхняя правая часть показывает логическую структуру (синтаксическое дерево) выражения с "." обозначает конкатенацию (предполагается, что арность переменной); подвыражения названы а-q для справочных целей. В левой части показан недетерминированный конечный автомат, полученный в результате алгоритма Томпсона, с Вход и выход состояние каждого подвыражения, окрашенного в пурпурный и голубойДля ясности обозначение перехода ε опущено - немаркированные переходы на самом деле являются переходами ε. Состояние входа и выхода, соответствующее корневому выражению q - состояние запуска и приема автомата соответственно.
Шаги алгоритма следующие:
| q: | начать преобразовывать выражение звезды Клини | (0|(1(01*(00)*0)*1)*)* | ||||||||
| б: | начать преобразование выражения объединения | 0|(1(01*(00)*0)*1)* | ||||||||
| а: | преобразовать символ | 0 | ||||||||
| п: | начать преобразовывать выражение звезды Клини | (1(01*(00)*0)*1)* | ||||||||
| d: | начать преобразование выражения конкатенации | 1(01*(00)*0)*1 | ||||||||
| c: | преобразовать символ | 1 | ||||||||
| п: | начать преобразовывать выражение звезды Клини | (01*(00)*0)* | ||||||||
| ж: | начать преобразование выражения конкатенации | 01*(00)*0 | ||||||||
| е: | преобразовать символ | 0 | ||||||||
| час: | начать преобразовывать выражение звезды Клини | 1* | ||||||||
| грамм: | преобразовать символ | 1 | ||||||||
| час: | закончил преобразование выражения звезды Клини | 1* | ||||||||
| л: | начать преобразовывать выражение звезды Клини | (00)* | ||||||||
| j: | начать преобразование выражения конкатенации | 00 | ||||||||
| я: | преобразовать символ | 0 | ||||||||
| k: | преобразовать символ | 0 | ||||||||
| j: | завершено преобразование выражения конкатенации | 00 | ||||||||
| л: | закончил преобразование выражения звезды Клини | (00)* | ||||||||
| м: | преобразовать символ | 0 | ||||||||
| ж: | завершено преобразование выражения конкатенации | 01*(00)*0 | ||||||||
| п: | закончил преобразование выражения звезды Клини | (01*(00)*0)* | ||||||||
| о: | преобразовать символ | 1 | ||||||||
| d: | завершено преобразование выражения конкатенации | 1(01*(00)*0)*1 | ||||||||
| п: | закончил преобразование выражения звезды Клини | (1(01*(00)*0)*1)* | ||||||||
| б: | завершено преобразование выражения объединения | 0|(1(01*(00)*0)*1)* | ||||||||
| q: | закончил преобразование выражения звезды Клини | (0|(1(01*(00)*0)*1)*)* | ||||||||
Ниже показан эквивалентный минимальный детерминированный автомат.
Отношение к другим алгоритмам
Алгоритм Томпсона - один из нескольких алгоритмов построения NFA из регулярных выражений;[5] более ранний алгоритм был предложен Макнотоном и Ямадой.[6] Обратимся к конструкции Томпсона, Алгоритм Клини преобразует конечный автомат в регулярное выражение.
Алгоритм построения Глушкова аналогична конструкции Томпсона после удаления ε-переходов.
Рекомендации
| Викискладе есть медиафайлы по теме Конструкция Томпсона (формальная теория языка). |
- ^ а б c Альфред Вайно Ахо; Моника С. Лам; Рави Сетхи; Джеффри Д. Уллман (2007). «3.7.4 Построение NFA из регулярного выражения» (Распечатать). Компиляторы: принципы, методы и инструменты (2-е изд.). Бостон, Массачусетс, США: Пирсон Аддисон-Уэсли. п.159–163. ISBN 9780321486813.
- ^ Лауден, Кеннет С. (1997). «2.4.1 От регулярного выражения к NFA» (Распечатать). Построение компилятора: принципы и практика (3-е изд.). 20 Park Plaza Boston, MA 02116-4324, США: PWS Publishing Company. С. 64–69. ISBN 978-0-534-93972-4.CS1 maint: location (связь)
- ^ Кен Томпсон (июнь 1968 г.). «Методы программирования: алгоритм поиска регулярных выражений». Коммуникации ACM. 11 (6): 419–422. Дои:10.1145/363347.363387.
- ^ Син, Гуанмин. «Свернутая NFA Томпсона» (PDF).
- ^ Уотсон, Брюс В. (1995). Таксономия алгоритмов построения конечных автоматов (PDF) (Технический отчет). Эйндховенский технологический университет. Отчет о вычислительной науке 93/43.
- ^ Р. Макнотон, Х. Ямада (март 1960 г.). "Регулярные выражения и графы состояний для автоматов". Транзакции IEEE на электронных компьютерах. 9 (1): 39–47. Дои:10.1109 / TEC.1960.5221603.