WikiDer > Фазовая кривая (астрономия)

Phase curve (astronomy)

В астрономии фазовая кривая описывает яркость отражающего тела как функцию его угол фазы. Яркость обычно относится к объекту абсолютная величина, что, в свою очередь, является его кажущаяся величина на расстоянии астрономическая единица с Земли и Солнца. В угол фазы равняется дуге, создаваемой наблюдателем, и солнцу, измеренному на теле.

Фазовая кривая полезна для характеристики объекта реголит (почва) и атмосфера. Это также основа для вычисления геометрическое альбедо и Связанное альбедо тела. В эфемериды генерации, фазовая кривая используется вместе с расстояниями от объекта до Солнца и Земли для расчета видимой звездной величины.

Меркурий

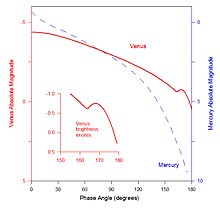
Фазовая кривая Меркурий и всплеск его сопротивления.[1]

Фазовая кривая Меркурий очень крутой, что характерно для тела, на котором голый реголит (почва) выставлена ​​на обозрение. При фазовых углах более 90 ° (полумесяц фаза) особенно резко падает яркость. Форма фазовой кривой указывает на средний наклон на поверхности Меркурия около 16 °,[1] который немного более гладкий, чем у Луна. При приближении фазового угла к 0 ° (полностью освещенная фаза) кривая поднимается до резкого пика. Этот всплеск яркости называется эффект противодействия[2][3] потому что для большинства тел (за исключением Меркурия) это происходит при астрономической оппозиции, когда тело противоположно Солнцу на небе. Ширина волны оппозиции для Меркурия указывает на то, что как состояние уплотнения реголита, так и распределение размеров частиц на планете аналогичны таковым на Луне.[1]

Ранние визуальные наблюдения, вносящие вклад в фазовую кривую Меркурия, были получены Г. Мюллером.[4] в 1800-х годах и позже Андре-Луи Данжон[5][6][7] в середине ХХ века. В. Ирвин и его коллеги[8] использовал фотоэлектрическую фотометрию в 1960-х годах. Некоторые из этих ранних данных были проанализированы G. de Vaucouleurs,[9][10] обобщено Д. Харрисом[11] и используется для предсказания видимых звездных величин в Астрономический альманах[12] в течение нескольких десятилетий. Новые высокоточные наблюдения, охватывающие самый широкий на сегодняшний день диапазон фазовых углов (от 2 до 170 °), были выполнены А. Малламой, Д. Вангом и Р. Ховардом.[1] с использованием Широкоугольный и спектрометрический коронограф (LASCO) на Солнечная и гелиосферная обсерватория (SOHO) спутник. Они также получили новые наблюдения ПЗС с земли. Эти данные в настоящее время являются основным источником фазовой кривой, используемой в Астрономический альманах[13] для предсказания видимых звездных величин.

Видимая яркость Меркурия с Земли максимальна при фазовом угле 0 ° (высшее соединение с Солнцем), когда он может достигать величины −2,6.[14] При фазовых углах, приближающихся к 180 ° (нижнее соединение) планета исчезает примерно до +5 звездной величины[14] с точной яркостью в зависимости от фазового угла на данном конкретном соединение. Эта разница более чем в 7 звездных величин соответствует изменению видимой яркости более чем в тысячу раз.

Венера

Фазовая кривая Венеры[15] по сравнению с Меркурием,[1] и избыток яркости Венеры.

Относительно плоская фазовая кривая Венера характерна для облачной планеты.[14] В отличие от Меркурия, где кривая имеет сильный пик, приближающийся к нулю фазового угла (полная фаза), у Венеры закругленная. Широкий угол рассеяния света облаками, в отличие от более узкого рассеяния реголита, вызывает такое сглаживание фазовой кривой. На Венере наблюдается всплеск яркости вблизи фазового угла 170 °, когда она тонкая. полумесяц, из-за прямого рассеяния солнечного света каплями серная кислота которые находятся над вершинами облаков планеты.[15] Даже за пределами 170 ° яркость не сильно падает.

История наблюдений и анализа фазовой кривой Венеры аналогична истории Меркурия. Лучший набор современных наблюдений и интерпретаций был предоставлен А. Малламой, Д. Вангом и Р. Ховардом.[15] Они использовали ЛАСКО инструмент на SOHO и наземное оборудование ПЗС для наблюдения за фазовой кривой от 2 до 179 °. Как и в случае с Меркурием, эти новые данные являются основным источником фазовой кривой, используемой в Астрономический альманах[13] для предсказания видимых звездных величин.

В отличие от Меркурия максимальная видимая яркость Венеры, видимой с Земли, не происходит при нулевом фазовом угле. Поскольку фазовая кривая Венеры относительно плоская, а расстояние до Земли может сильно варьироваться, максимальная яркость достигается, когда планета представляет собой серп с фазовым углом 125 °, при этом яркость Венеры может достигать -4,9 звездной величины.[14] Возле нижнее соединение планета обычно исчезает примерно до -3 звездной величины.[14] хотя точное значение зависит от фазового угла. Типичный диапазон видимой яркости Венеры в течение одного явления составляет менее 10 раз или всего 1% от яркости Меркурия.

земной шар

Фазовая кривая земной шар не был определен так точно, как для Меркурия и Венеры, потому что его интегральную яркость трудно измерить с поверхности. Вместо прямого наблюдения земляной свет отражение от части Луны, не освещенной Солнцем, служило прокси. Несколько прямых измерений светимости Земли были получены с помощью EPOXI космический корабль. Хотя они не покрывают большую часть фазовой кривой, они показывают вращательную кривую блеска, вызванную прохождением темных океанов и ярких масс суши через полушарие. П. Гуд и его коллеги из Солнечная обсерватория Big Bear измерили земной свет[16] и Т. Ливенгуд из НАСА проанализировали данные EPOXI.[17]

Земля, если смотреть с Венеры вблизи от Солнца, будет чрезвычайно яркой с блеском -6. Наблюдателю, находящемуся за пределами орбиты Земли на Марсе, наша планета могла бы казаться наиболее яркой во время ее наибольшего удлинения от Солнца, примерно с величиной -1,5.

Марс

Фазовая кривая Марса[18] по сравнению с Меркурием.[1]

Только около 50 ° марсианской фазовой кривой можно наблюдать с Земли, потому что она движется по орбите дальше от Солнца, чем наша планета. Есть всплеск оппозиции, но он менее выражен, чем у Меркурия. Вращение ярких и темных отметок на поверхности диска и изменчивость состояния атмосферы (включая пылевые бури) накладывают изменения на фазовую кривую. Р. Шмуде[19][20] получил многие из Марс измерения яркости, использованные в комплексном анализе фазовой кривой, выполненном А. Малламой.[18]

Поскольку орбита Марса значительно эксцентрична, его яркость в оппозиции может варьироваться от -3,0 до -1,4.[14] Минимальная яркость - около +1,6 звездной величины.[14] когда Марс находится на противоположном от Земли участке Солнца. Изменения вращения могут увеличивать или уменьшать яркость Марса на 5%, а глобальные пыльные бури могут увеличивать его светимость на 25%.[14][18]

Газовые гиганты

Самые дальние планеты (Юпитер, Сатурн, Уран, и Нептун) настолько далеки, что с Земли можно оценить лишь небольшие участки их фазовых кривых около 0 ° (полная фаза). Эта часть кривой обычно довольно плоская, как у Венеры для этих облачных планет.

Видимая величина Юпитера составляет от -2,9 до -1,4, Сатурна от -0,5 до +1,4, Урана от +5,3 до +6,0 и Нептуна от +7,8 до +8,0. Большинство этих изменений связано с расстоянием. Однако диапазон звездных величин Сатурна также зависит от его кольцевой системы, как описано ниже.

Смотрите также: Газовые гиганты

Кольца Сатурна

Фазовая кривая Сатурна по Шмуде[21] демонстрируя противодействие кольцевой системы.

Яркость системы Сатурна зависит от ориентации его кольцевая система. Кольца вносят больший вклад в общую яркость системы, когда они больше наклонены к направлению освещения от Солнца и к обзору наблюдателя. Широко открытые кольца дают яркость только диску примерно на одну величину.[14] Ледяные частицы, из которых состоят кольца, также создают сильный всплеск сопротивления. Снимки космического телескопа Хаббла и космического корабля Кассини были проанализированы в попытке охарактеризовать кольцевые частицы на основе их фазовых кривых.[22][23][24][25]

Луна

Фазовая кривая Луны[26] по сравнению с Меркурием.[1]

Фазовая кривая Луна приблизительно напоминает Меркурий из-за сходства поверхностей и отсутствия атмосферы на обоих телах.[27] Клементина данные космического корабля проанализированы Дж. Хиллиером, Б. Буратти и К. Хиллом.[28] указывают на лунный всплеск оппозиции. Видимая звездная величина Луны в полную фазу составляет -12,7.[29] в то время как в четверть фазы он на 21 процент ярче.[26]

Планетарные спутники

Фазовые кривые многих естественные спутники других планет[30][31] наблюдались и интерпретировались. Ледяные луны часто демонстрируют всплески противоположной яркости. Это поведение использовалось для моделирования их поверхностей.

Астероиды

Фазовые кривые многих астероиды[32] также наблюдались, и они тоже могут демонстрировать всплески сопротивления. Таким образом можно физически классифицировать астероиды.[33] Эффект вращения может быть очень большим, и его необходимо учесть перед вычислением фазовой кривой. Пример такого исследования сообщают Р. Бейкер и его коллеги.[34]

Экзопланеты

Программы для описания планет за пределами Солнечной системы во многом зависят от спектроскопии для определения компонентов и состояний атмосферы, особенно тех, которые указывают на присутствие форм жизни или которые могут поддерживать жизнь. Однако яркость можно измерить для очень далеких объектов размером с Землю, которые слишком тусклые для спектроскопического анализа. А. Маллама[35] продемонстрировал, что анализ фазовой кривой может быть полезным инструментом для идентификации планет, похожих на Землю. Кроме того, Дж. Бейли[36] указал, что аномалии фазовой кривой, такие как превышение яркости Венеры могут быть полезными индикаторами компонентов атмосферы, таких как вода, которые могут иметь важное значение для жизнь во вселенной.

Смотрите также: Экзопланеты

Критика моделирования фазовой кривой

Выводы о реголитах из фазовых кривых часто основываются на Параметризация Хапке. Однако в слепом тесте М. Шепард и П. Хельфенштейн[37] не обнаружили убедительных доказательств того, что конкретный набор Параметры Хапке полученные на основе фотометрических данных могут однозначно показать физическое состояние лабораторных образцов. Эти тесты включали моделирование трехчленных фазовых функций Хеньи-Гринштейна и эффекта оппозиции когерентного обратного рассеяния. Этот отрицательный результат предполагает, что модель переноса излучения, разработанная Б. Хапке может быть неадекватным для физического моделирования на основе фотометрии.

Рекомендации

  1. ^ а б c d е ж грамм Маллама, А .; Wang, D .; Ховард, Р. (2002). «Фотометрия Меркурия с SOHO / LASCO и Земли». Икар. 155 (2): 253–264. Bibcode:2002Icar..155..253M. Дои:10.1006 / icar.2001.6723.
  2. ^ Шкуратов Ю.Г., Креславский М.А., Овчаренко А.А., Станкевич Д.Г., Зубко Е.С. (1999). «Оппозиционный эффект от данных Клементина и механизмы обратного рассеяния». Икар. 141 (1): 132–155. Bibcode:1999Icar..141..132S. Дои:10.1006 / icar.1999.6154.CS1 maint: несколько имен: список авторов (связь)
  3. ^ Helfenstein, P., Veverka, J., and Hillier, J. (1997). «Эффект лунного противостояния: испытание альтернативных моделей». Икар. 128 (1): 2–14. Bibcode:1997Icar..128 .... 2H. Дои:10.1006 / icar.1997.5726.CS1 maint: несколько имен: список авторов (связь)
  4. ^ Мюллер, Г. (1893). "Helligkeitsbestimmungen der grossen planeten und einiger asteroiden". Publ. Astrophys. Обс. Потсдам. 8 (92): 197–398.
  5. ^ Данжон, А. (1949). «Фотометрия и колориметрия планет Меркурия и Венеры». Бык. Astron. 14: 315–345. Bibcode:1949БуАст..14..315Д.
  6. ^ Данжон, А. (1950). «Поправка к Данжону 1949 года». Бык. Astron. 14: 315.
  7. ^ Данжон, А. (1953). «Поправка к Данжону 1949 года». Бык. Astron. 17: 363.
  8. ^ Ирвин, У. Х., Т. Саймон, Д. Х. Мензель, К. Пикос и А. Т. Янг (1968). «Многоцветная фотоэлектрическая фотометрия ярких планет III». Astron. J. 73: 807–828. Bibcode:1968AJ ..... 73..807I. Дои:10.1086/110702.CS1 maint: несколько имен: список авторов (связь)
  9. ^ де Вокулёр Г. (1964). «Геометрические и фотометрические параметры планет земной группы». Икар. 3 (3): 187–235. Bibcode:1964Icar .... 3..187D. Дои:10.1016/0019-1035(64)90018-1.
  10. ^ deVaucouleurs, G. (1970). А. Дольфус (ред.). в Поверхности и недрах планет и спутников. Академическая пресса. п. 225.
  11. ^ Харрис, Д.Л. (1961). Г.П. Койпер и Б.А. Миддлхерст (ред.). в планетах и ​​спутниках. U. Chicago Press. п. 272.
  12. ^ Хилтон, Дж. Л. (1992). П.К. Зайдельманн (ред.). в пояснительном приложении к астрономическому альманаху. Книги университетских наук. п. 383.
  13. ^ а б Хилтон, Дж. Л. (2005). «Улучшение визуальных величин планет в астрономическом альманахе. I. Меркурий и Венера». Astron. J. 129 (6): 2902–2906. Bibcode:2005AJ .... 129.2902H. Дои:10.1086/430212.
  14. ^ а б c d е ж грамм час я Маллама, А. (2011). «Планетарные величины». Небо и телескоп. 121 (1): 51–56.
  15. ^ а б c Маллама, А .; Wang, D .; Ховард, Р. (2006). "Фазовая функция Венеры и рассеяние вперед от H2ТАК4". Икар. 182 (1): 10–22. Bibcode:2006Icar..182 ... 10M. Дои:10.1016 / j.icarus.2005.12.014.
  16. ^ Гуд П.Р., Цю Дж., Юрчишин В., Хики Дж., Чу М.С., Кольбе Э., Браун С.Т. и Кунин С.Е. (2001). "Наблюдения за коэффициентом отражения Земли с помощью солнечного света" (PDF). Geophys. Res. Латыш. 28 (9): 1671–1674. Bibcode:2001GeoRL..28.1671G. Дои:10.1029 / 2000GL012580.CS1 maint: несколько имен: список авторов (связь)
  17. ^ Ливенгуд Т. и 10 соавторов (2008). «Эмпирический тест EPOXI для определения оптических характеристик планеты земного типа». Бык. Являюсь. Astron. Soc. 40: Презентация 01.03. Bibcode:2008ДПС .... 40.0103Л.CS1 maint: несколько имен: список авторов (связь)
  18. ^ а б c Маллама, А. (2007). «Величина и альбедо Марса». Икар. 192 (2): 404–416. Bibcode:2007Icar..192..404M. Дои:10.1016 / j.icarus.2007.07.011.
  19. ^ Шмуде, Р. В. Младший (2004). "Наблюдения ALPO явления Марса в 2003 г.". J. Assoc. Лунная планета. Наблюдать. 46 (4): 28–42 и ссылки в нем. Bibcode:2004 ЯЛПО..46д..28С.
  20. ^ Шмуде, Р. В. Младший (2006). «Широкополосная фотометрия Марса: 1991–2006 гг.». Бык. Являюсь. Astron. Soc. 38 (3): 600 и ссылки в нем. Bibcode:2006ДПС .... 38.6014С.
  21. ^ Шмуде, Р. В. Младший (2011). «Величина и цвет системы Сатурна». Икар. 211 (1): 732–739. Bibcode:2011Icar..211..732S. Дои:10.1016 / j.icarus.2010.09.018.
  22. ^ Френч, Р.Г., Вербисер, А., Сало, Х., МакГи, К., и Донес, Л. (2007). "Кольца Сатурна в истинном противостоянии". Publ. Astron. Soc. Pac. 119 (856): 623–643. Bibcode:2007PASP..119..623F. Дои:10.1086/519982.CS1 maint: несколько имен: список авторов (связь)
  23. ^ Пуле, Ф., Куззи, Дж. Н., Френч, Р. Г., Донес, Л. (2002). «Исследование фазовых кривых кольца Сатурна по наблюдениям HST». Икар. 158 (1): 224–248. Bibcode:2002Icar..158..224P. Дои:10.1006 / icar.2002.6852.CS1 maint: несколько имен: список авторов (связь)
  24. ^ Куцци, Дж. Н., Френч, Р. Г., Донес, Л. (2002). «Многоцветная (255–1042 нм) фотометрия главных колец Сатурна HST». Икар. 158 (1): 199–223. Bibcode:2002Icar..158..199C. Дои:10.1006 / icar.2002.6851.CS1 maint: несколько имен: список авторов (связь)
  25. ^ Сало, H .; Френч, Р. Г. (2010). «Противопоставление и эффект наклона колец Сатурна по наблюдениям HST». Икар. 210 (2): 785–816. arXiv:1007.0349. Bibcode:2010Icar..210..785S. Дои:10.1016 / j.icarus.2010.07.002.
  26. ^ а б Кокс, А. (2000). Астрофизические величины Аллена, четвертое издание. Springer-Verlag. С. 307–310.
  27. ^ Уорелл, Дж. (2004). «Свойства германского реголита: IV. Фотометрические параметры Меркурия и Луны в сравнении с моделированием Хапке». Икар. 167 (2): 271–286. Bibcode:2004Icar..167..271W. Дои:10.1016 / j.icarus.2003.10.010.
  28. ^ Хиллер Дж., Буратти Б. и Хилл К. (1999). «Мультиспектральная фотометрия Луны и абсолютная калибровка камеры Clementine UV / VIS». Икар. 141 (2): 205–225. Bibcode:1999Icar..141..205H. Дои:10.1006 / icar.1999.6184.CS1 maint: несколько имен: список авторов (связь)
  29. ^ Уильямс, доктор Дэвид Р. (02.02.2010). "Информационный бюллетень о Луне". НАСА (Национальный центр данных по космическим наукам). Получено 2010-11-17.
  30. ^ Бауэр, Дж. М., Грав, Т., Буратти, Б. Дж. И Хикс, М. Д. (2006). "Обзор фазовой кривой нерегулярных спутников Сатурна: возможный метод физической классификации". Икар. 184 (1): 181–197. Bibcode:2006Icar..184..181B. Дои:10.1016 / j.icarus.2006.04.011.CS1 maint: несколько имен: список авторов (связь)
  31. ^ Деу, Э., Донес, Л., Родригес, С., Чарноз, С. и Брахич, А. (2009). «Эффект оппозиции во внешней Солнечной системе: сравнительное исследование морфологии фазовой функции». Планетарная и космическая наука. 57 (11): 1282–1301. arXiv:0902.0345. Bibcode:2009P & SS ... 57.1282D. Дои:10.1016 / j.pss.2009.05.005.CS1 maint: несколько имен: список авторов (связь)
  32. ^ Кокс, А. (2000). Астрофизические величины Аллена, четвертое издание. Springer-Verlag. п. 299.
  33. ^ Каасалайнен, С., Пийронен, Дж., Каасалайнен, М., Харрис, А.В., Муйнонен, К. и Челлино, А. (2003). «Фотометрические и поляриметрические фазовые кривые астероидов: эмпирическая интерпретация». Икар. 161 (1): 34–46. Bibcode:2003Icar..161 ... 34K. Дои:10.1016 / S0019-1035 (02) 00020-9.CS1 maint: несколько имен: список авторов (связь)
  34. ^ Бейкер, Р.Е., Бенишек, В., Пилчер, Ф., и Хиггинс, Д.; Бенишек; Пилчер; Хиггинс (2010). «Период вращения и определение параметров H-G для 1700 Звезды: совместный фотометрический проект». Бюллетень Малой планеты. 37 (3): 81–83. Bibcode:2010MPBu ... 37 ... 81B.CS1 maint: несколько имен: список авторов (связь)[постоянная мертвая ссылка]
  35. ^ Маллама, А. (2009). «Характеристика экзопланет земного типа на основе фазовых кривых и альбедо Меркурия, Венеры и Марса». Икар. 204 (1): 11–14. Bibcode:2009Icar..204 ... 11M. Дои:10.1016 / j.icarus.2009.07.010.
  36. ^ Бейли, Дж. (2007). «Радуга, поляризация и поиск обитаемых планет». Астробиология. 7 (2): 320–332. Bibcode:2007 AsBio ... 7..320B. Дои:10.1089 / аст.2006.0039. PMID 17480163.
  37. ^ Шепард, М. К. и Хельфенштейн, П. (2007). «Тест фотометрической модели Хапке». J. Geophys. Res. 112 (E3): E03001. Bibcode:2007JGRE..112.3001S. Дои:10.1029 / 2005JE002625.