WikiDer > Мутация принята в точке - Википедия

Пример точечных мутаций в аминокислотном сайте, кодирующем лизин. В миссенс-мутации могут быть классифицированы как точечные принятые мутации, если мутировавший белок не отвергается естественным отбором.

А точка принятая мутация - также известный как PAM - это замена одного аминокислота в первичная структура из белок с другой единственной аминокислотой, которая принимается процессами естественный отбор. Это определение не включает все точечные мутации в ДНК организма. Особенно, тихие мутации не являются точечно принятыми мутациями, равно как и мутациями, которые не являются летальными или которые отвергаются естественным отбором другими способами.

А Матрица PAM это матрица где каждый столбец и строка представляют одну из двадцати стандартных аминокислот. В биоинформатика, Матрицы PAM регулярно используются как матрицы замещения набрать выравнивание последовательностей для белков. Каждая запись в матрице PAM указывает вероятность того, что аминокислота в этой строке будет заменена аминокислотой из этого столбца в результате серии из одной или нескольких точечных принятых мутаций в течение указанного эволюционного интервала, а не эти две аминокислоты будут выровнены должным образом. к случаю. Разные матрицы PAM соответствуют разным временам эволюции белковой последовательности.

Биологический фон

Генетические инструкции каждой репликации клетка в живом организме содержатся в его ДНК.^[1] На протяжении всей жизни клетки эта информация транскрибируется и реплицируется клеточными механизмами для производства белков или предоставления инструкций дочерним клеткам во время деление клеток, и существует вероятность того, что ДНК может быть изменена во время этих процессов.^[1][2] Это известно как мутация. На молекулярном уровне существуют регуляторные системы, которые корректируют большую часть - но не все - этих изменений в ДНК до того, как она будет реплицирована.^[2][3]

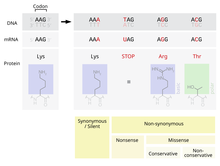
Одна из возможных мутаций - это замена одного нуклеотид, известная как точечная мутация. Если точечная мутация происходит в экспрессируемой области ген, экзон, то это изменит кодон определение конкретной аминокислоты в белке, продуцируемом этим геном.^[2] Несмотря на избыточность в генетический код, есть вероятность, что эта мутация изменит аминокислоту, которая вырабатывается во время перевод, и, как следствие, изменится структура белка.

Функциональность протеина сильно зависит от его структуры.^[4] Изменение одной аминокислоты в белке может снизить его способность выполнять эту функцию, или мутация может даже изменить функцию, которую выполняет белок.^[2] Подобные изменения могут серьезно повлиять на важную функцию клетки, потенциально вызывая смерть клетки, а в крайних случаях и организма.^[5] И наоборот, изменение может позволить клетке продолжать функционировать, хотя и по-другому, и мутация может быть передана потомству организма. Если это изменение не приведет к какому-либо значительному физическому ущербу для потомства, существует вероятность того, что эта мутация сохранится в популяции. Также существует возможность того, что изменение функции станет выгодным. В любом случае, подвергаясь процессам естественного отбора, точечная мутация была принята в генетический пул.

20 аминокислот, транслируемых генетическим кодом, сильно различаются по физическим и химическим свойствам их боковых цепей.^[4] Однако эти аминокислоты можно разделить на группы со схожими физико-химическими свойствами.^[4] Замена аминокислоты другой из той же категории с большей вероятностью окажет меньшее влияние на структуру и функцию белка, чем замена аминокислотой из другой категории. Следовательно, принятие точечных мутаций сильно зависит от аминокислоты, заменяемой в мутации, и заменяемой аминокислоты. Матрицы PAM представляют собой математический инструмент, который учитывает эти различные скорости принятия при оценке сходства белков во время выравнивания.

Терминология

Период, термин принятая точечная мутация изначально использовался для описания феномена мутации. Однако аббревиатура PAM была предпочтительнее APM из-за удобочитаемости, поэтому термин точка принятая мутация используется более регулярно.^[6] Потому что ценность ${ displaystyle n}$ в PAM_п матрица представляет собой количество мутаций на 100 аминокислот, которое можно сравнить с процентом мутаций, термин процент принятых мутаций иногда используется.

Важно различать точечные принятые мутации (PAM), точечно принятые матрицы мутаций (PAM-матрицы) и PAM._п матрица. Термин «точечная принятая мутация» относится к самому событию мутации. Однако «матрица PAM» относится к одной из семейства матриц, которые содержат оценки, представляющие вероятность выравнивания двух аминокислот из-за серии событий мутации, а не из-за случайной случайности. 'PAM_п matrix '- матрица PAM, соответствующая временному кадру, достаточно длинному для ${ displaystyle n}$ события мутации происходят на 100 аминокислот.

Построение матриц PAM

Матрицы PAM были введены Маргарет Дейхофф в 1978 г.^[7] Расчет этих матриц был основан на 1572 наблюдаемых мутациях в филогенетические деревья из 71 семейства близкородственных белков. Исследуемые белки были отобраны на основе их высокого сходства со своими предшественниками. Включенные белковые выравнивания должны были показать идентичность по крайней мере на 85%.^[6][8] В результате разумно предположить, что любые выровненные несоответствия были результатом одного события мутации, а не нескольких в одном месте.

Каждая матрица PAM состоит из двадцати строк и двадцати столбцов, по одному представлению каждой из двадцати аминокислот, транслируемых генетическим кодом. Значение в каждой ячейке матрицы PAM связано с вероятностью того, что аминокислота строки до мутации впоследствии будет выровнена с аминокислотой столбца.^[6][7][8] Из этого определения матрицы PAM являются примером матрица замещения.

Сбор данных с филогенетических деревьев

Для каждой ветви филогенетических деревьев семейств белков регистрировалось количество наблюдаемых несоответствий и велись записи для двух задействованных аминокислот.^[7] Эти подсчеты использовались как записи ниже главной диагонали матрицы ${ displaystyle A}$. Поскольку подавляющее большинство образцов белка поступает от организмов, которые живы сегодня (существующие виды), «направление» мутации не может быть определено. То есть аминокислоту, присутствующую до мутации, нельзя отличить от аминокислоты, которая заменила ее после мутации. Из-за этого матрица ${ displaystyle A}$ предполагается симметричный, а записи ${ displaystyle A}$ выше главной диагонали вычисляются на этой основе. Записи по диагонали ${ displaystyle A}$ не соответствуют мутациям и могут быть оставлены незаполненными.

В дополнение к этим подсчетам были получены данные об изменчивости и частоте аминокислот.^[6][7] Изменчивость аминокислоты - это соотношение количества мутаций, в которых она участвует, и количества раз, когда она встречается в выравнивании.^[7] Мутабельность измеряет вероятность приемлемой мутации аминокислоты. Аспарагин, аминокислота с небольшим полярный боковая цепь, как было обнаружено, является наиболее изменчивой из аминокислот.^[7] Цистеин и триптофан оказались наименее изменчивыми аминокислотами.^[7] Боковые цепи цистеина и триптофана имеют менее распространенные структуры: боковая цепь цистеина содержит серу, которая участвует в дисульфидные связи с другими молекулами цистеина, а боковая цепь триптофана большая и ароматный.^[4] Поскольку существует несколько небольших полярных аминокислот, эти крайности предполагают, что аминокислоты более склонны к приемлемой мутации, если их физические и химические свойства более распространены среди альтернативных аминокислот.^[6][8]

Построение матрицы мутаций

Для ${ displaystyle j}$-я аминокислота, значения ${ displaystyle m (j)}$ и ${ displaystyle f (j)}$ его изменчивость и частота. Частоты аминокислот нормализованы так, чтобы они в сумме равнялись 1. Если общее количество вхождений ${ displaystyle j}$-я аминокислота ${ displaystyle n (j)}$, и ${ displaystyle N}$ - общее количество всех аминокислот, тогда

${ displaystyle f (j) = { frac {n (j)} {N}}}$

На основе определения изменчивости как отношения мутаций к количеству встречаемости аминокислоты.

${ displaystyle m (j) = { frac { sum _ {i = 1, i neq j} ^ {20} A (i, j)} {n (j)}}}$

или же

${ displaystyle { frac {1} {Nf (j)}} = { frac {1} {n (j)}} = { frac {m (j)} { sum _ {i = 1, i neq j} ^ {20} A (i, j)}}}$

Матрица мутаций ${ displaystyle M}$ построен так, что запись ${ Displaystyle M (я, j)}$ представляет собой вероятность ${ displaystyle j}$-я аминокислота мутирует в ${ displaystyle i}$-я аминокислота. Недиагональные элементы вычисляются по уравнению^[7]

${ Displaystyle M (я, j) ​​= лямбда A (i, j) { гидроразрыва {m (j)} { sum _ {i = 1, i neq j} ^ {20} A (i, j )}} = { frac { lambda A (i, j)} {Nf (j)}}}$

куда ${ displaystyle lambda}$ - константа пропорциональности. Однако это уравнение не вычисляет диагональные элементы. Каждый столбец в матрице ${ displaystyle M}$ перечисляет каждый из двадцати возможных результатов для аминокислоты - она ​​может мутировать в одну из 19 других аминокислот или оставаться неизменной. Поскольку недиагональные записи, перечисляющие вероятности каждой из 19 мутаций, известны, а сумма вероятностей этих двадцати исходов должна быть равна 1, эту последнюю вероятность можно рассчитать следующим образом:

${ Displaystyle M (J, J) = 1- сумма _ {я = 1, я neq j} ^ {20} M (я, j)}$

что упрощает^[7]

${ Displaystyle М (J, J) = 1- лямбда м (J)}$

Расчет диагональных входов

${ Displaystyle M (J, J) = 1- сумма _ {я = 1, я neq j} ^ {20} M (я, j)}$ Подставляя выражение для матрицы мутаций недиагональных элементов: ${ Displaystyle M (J, J) = 1- сумма _ {я = 1, я neq j} ^ {20} { frac { lambda m (j) A (i, j)} { sum _ {i = 1, i neq j} ^ {20} A (i, j)}}}$ ${ Displaystyle M (j, j) = 1 - { frac { sum _ {i = 1, i neq j} ^ {20} lambda m (j) A (i, j)} { sum _ {i = 1, i neq j} ^ {20} A (i, j)}}}$ Поскольку значения ${ displaystyle lambda}$ и ${ displaystyle m (j)}$ константы, которые не изменяются со значением ${ displaystyle i}$ ${ Displaystyle M (j, j) = 1 - { frac { lambda m (j) sum _ {i = 1, i neq j} ^ {20} A (i, j)} { sum _ {i = 1, i neq j} ^ {20} A (i, j)}}}$ Таким образом, отмена показывает, что ${ Displaystyle М (J, J) = 1- лямбда м (J)}$

Особенно важным результатом является то, что для недиагональных элементов

${ Displaystyle F (J) M (I, J) = { frac { lambda} {N}} A (I, J) = { frac { lambda} {N}} A (j, i) = f (i) M (j, i)}$

Это означает, что для всех записей в матрице мутаций

${ Displaystyle F (J) M (I, J) = F (I) M (J, I)}$

Выбор константы пропорциональности

Вероятности, содержащиеся в ${ displaystyle M}$ варьируются как некоторая неизвестная функция количества времени, в течение которого белковой последовательности позволяют мутировать. Вместо того, чтобы пытаться определить эту взаимосвязь, значения ${ displaystyle M}$ рассчитываются для короткого периода времени, а матрицы для более длительных периодов времени рассчитываются исходя из предположения, что мутации следуют Цепь Маркова модель.^[9][10] Базовая единица времени для матриц PAM - это время, необходимое для возникновения 1 мутации на 100 аминокислот, иногда называемое «единицей PAM» или «PAM» времени.^[6] Это как раз продолжительность мутации, предполагаемая PAM.₁ матрица.

Постоянная ${ displaystyle lambda}$ используется для контроля доли неизмененных аминокислот. Используя только выравнивания белков, которые имели сходство не менее 85%, можно было разумно предположить, что наблюдаемые мутации были прямыми, без каких-либо промежуточных состояний. Это означает, что уменьшение этих подсчетов с помощью общего фактора обеспечило бы точную оценку количества мутаций, если бы сходство было ближе к 100%. Это также означает, что количество мутаций на 100 аминокислот, ${ displaystyle n}$ в ПАМ_п равно количеству мутировавших аминокислот на 100 аминокислот.

Чтобы найти матрицу мутаций для PAM₁ матрице предъявляется требование, чтобы 99% аминокислот в последовательности были консервативными. Количество ${ Displaystyle N (J) M (J, J)}$ равно количеству консервативной аминокислоты ${ displaystyle j}$ единиц, и поэтому общее количество консервативных аминокислот составляет

${ displaystyle sum _ {j = 1} ^ {20} n (j) M (j, j) = sum _ {j = 1} ^ {20} n (j) - lambda sum _ {j = 1} ^ {20} n (j) m (j) = NN lambda sum _ {j = 1} ^ {20} f (j) m (j)}$

Значение ${ displaystyle lambda}$ необходимо выбрать, чтобы получить 99% идентичности после мутации, затем задается уравнением

${ Displaystyle 0,99 = 1- лямбда сумма _ {j = 1} ^ {20} f (j) m (j)}$

Этот ${ displaystyle lambda}$ значение затем можно использовать в матрице мутаций для PAM₁ матрица.

Строительство PAM_п матрицы

Модель мутации белков с марковской цепью связывает матрицу мутаций для PAM_п, ${ displaystyle M_ {n}}$, в матрицу мутаций для PAM₁ матрица ${ displaystyle M_ {1}}$ простыми отношениями

${ displaystyle M_ {n} = M_ {1} ^ {n}}$

ПАМ_п Матрица строится из отношения вероятностей точечных принятых мутаций, заменяющих ${ displaystyle j}$-я аминокислота с ${ displaystyle i}$-я аминокислота, к вероятности случайного выравнивания этих аминокислот._п матрицы задаются уравнением^[11][12]

${ displaystyle { text {PAM}} _ {n} (i, j) = log { frac {f (j) M_ {n} (i, j)} {f (i) f (j)}} = журнал { frac {f (j) M ^ {n} (i, j)} {f (i) f (j)}} = log { frac {M ^ {n} (i, j)} { f (i)}}}$

Обратите внимание, что в книге Гасфилда записи ${ Displaystyle M (я, j)}$ и ${ displaystyle { text {PAM}} _ {n} (я, j)}$ связаны с вероятностью ${ displaystyle i}$-я аминокислота мутирует в ${ displaystyle j}$-я аминокислота.^[11] Это источник различных уравнений для записей матриц PAM.

При использовании PAM_п матрицы для оценки выравнивания двух белков делается следующее предположение:

Если эти два белка связаны между собой, разделяющий их эволюционный интервал - это время, необходимое для ${ displaystyle n}$ указывают, что допустимые мутации происходят на 100 аминокислот.

Когда выравнивание ${ displaystyle i}$й и ${ displaystyle j}$th аминокислот, оценка показывает относительную вероятность выравнивания из-за того, что белки связаны или из-за случайной случайности.

• Если белки родственны, то должна была произойти серия точечных мутаций, которые привели к замене исходной аминокислоты. Предположим, что ${ displaystyle j}$-я аминокислота является исходной. Основываясь на содержании аминокислот в белках, вероятность ${ displaystyle j}$-я аминокислота является оригинальной ${ displaystyle f (j)}$. Учитывая любую конкретную единицу этой аминокислоты, вероятность быть замененным ${ displaystyle i}$-я аминокислота в предполагаемом интервале времени равна ${ Displaystyle M_ {п} (я, j)}$. Таким образом, вероятность совмещения равна ${ Displaystyle F (J) M_ {N} (I, J)}$, числитель с точностью до логарифма.
• Если белки не связаны, то события, что две выровненные аминокислоты являются ${ displaystyle i}$й и ${ displaystyle j}$аминокислоты должны быть независимый. Вероятности этих событий равны ${ Displaystyle f (я)}$ и ${ displaystyle f (j)}$, что означает, что вероятность совмещения равна ${ Displaystyle f (я) f (j)}$, знаменатель логарифма.
• Таким образом, логарифм в уравнении приводит к положительной записи, если выравнивание более вероятно из-за точечных мутаций, и к отрицательной записи, если выравнивание более вероятно из-за случайности.

Свойства матриц РАМ

Симметрия матриц РАМ

Тогда как матрица вероятности мутации ${ displaystyle M}$ не симметричен, каждая из матриц PAM.^[6][7] Это несколько удивительное свойство является результатом связи, отмеченной для матрицы вероятности мутации:

${ Displaystyle F (J) M (I, J) = F (I) M (J, I)}$

Фактически это соотношение выполняется для всех положительных целых степеней матрицы ${ displaystyle M}$:

${ Displaystyle F (J) M ^ {N} (I, J) = F (I) M ^ {N} (J, I)}$

Обобщение свойства на положительные целочисленные матричные степени

Это обобщение можно доказать, используя математическая индукция. Предположим, что для матрицы ${ displaystyle M}$ ${ Displaystyle F (J) M (I, J) = F (I) M (J, I)}$ И это для положительного целого числа ${ displaystyle k}$ ${ Displaystyle f (j) M ^ {k} (i, j) = f (i) M ^ {k} (j, i)}$ Путем расширения матричный продукт ${ Displaystyle M ^ {k + 1} = M ^ {k} cdot M}$, ${ Displaystyle f (j) M ^ {k + 1} (i, j) = f (j) sum _ {n = 0} ^ {N} M ^ {k} (i, n) M (n, j)}$ ${ Displaystyle f (j) M ^ {k + 1} (i, j) = sum _ {n = 0} ^ {N} M ^ {k} (i, n) (f (j) M (n , j))}$ Используя принятое нами свойство матрицы ${ displaystyle M}$ ${ Displaystyle е (j) M ^ {k + 1} (i, j) = sum _ {n = 0} ^ {N} M ^ {k} (i, n) (f (n) M (j , n))}$ ${ Displaystyle е (j) M ^ {k + 1} (i, j) = sum _ {n = 0} ^ {N} (f (n) M ^ {k} (i, n)) M ( j, n)}$ И используя свойство для матрицы ${ displaystyle M ^ {k}}$ ${ Displaystyle F (J) M ^ {K + 1} (I, J) = Sum _ {N = 0} ^ {N} (F (I) M ^ {K} (N, I)) M ( j, n)}$ ${ Displaystyle f (j) M ^ {k + 1} (i, j) = f (i) sum _ {n = 0} ^ {N} M (j, n) M ^ {k} (n, я)}$ ${ Displaystyle F (J) M ^ {K + 1} (I, J) = F (I) M ^ {K + 1} (J, I)}$ В этом случае сначала известно только, что результат верен для ${ displaystyle k = 1}$. Однако приведенный выше аргумент показывает, что это свойство также выполняется для ${ displaystyle k = 2}$. Это новое знание затем показывает, что это свойство также выполняется для ${ displaystyle k}$ и это повторяется, чтобы показать, что свойство выполняется для всех положительных целых чисел ${ displaystyle k}$.

В результате записи PAM_п матрицы симметричны, так как

${ displaystyle { text {PAM}} _ {n} (i, j) = log { frac {f (j) M ^ {n} (i, j)} {f (j) f (i)} } = журнал { frac {f (i) M ^ {n} (j, i)} {f (i) f (j)}} = { text {PAM}} _ {n} (j, i) }$

Связь количества мутировавших аминокислот и количества мутаций

Значение ${ displaystyle n}$ представляет собой количество мутаций, которые происходят на 100 аминокислот, однако это значение редко доступно и часто оценивается. Однако при сравнении двух белков легко вычислить ${ displaystyle m}$ вместо этого, это количество мутировавших аминокислот на 100 аминокислот. Несмотря на случайный характер мутации, эти значения могут быть приблизительно связаны соотношением^[13]

${ displaystyle { frac {m} {100}} = 1-e ^ {- { frac {n} {100}}}}$

Вывод родства между ${ displaystyle m}$ и ${ displaystyle n}$

Мутации в первичной структуре белка могут происходить в любом месте последовательности. Если предположить, что распределение мутаций по позициям аминокислот является однородным, проблема аналогична распределению «шариков по корзинам», распространенной проблеме в комбинаторика. В случае, когда ${ displaystyle K}$ шары (т.е. мутации) распределяются между ${ displaystyle N}$ бины (позиции аминокислот), количество бункеров, содержащих хотя бы один шар, ${ displaystyle M}$ имеет распределение со средним значением[14] ${ Displaystyle Е (М) = N-N (1 - { гидроразрыва {1} {N}}) ^ {K}}$ ${ displaystyle { frac {E (M)} {N}} = 1- (1 - { frac {1} {N}}) ^ {K}}$ Если скорость мутации ${ displaystyle n}$ мутации на 100 аминокислот, то ${ displaystyle { frac {n} {100}} = { frac {K} {N}}}$ И если есть ${ displaystyle m}$ мутировавших аминокислот на 100 аминокислот, то это примерно равно ${ displaystyle { frac {m} {100}} = { frac {E (M)} {N}}}$ Сейчас же ${ displaystyle m}$ и ${ displaystyle n}$ может быть связано ${ displaystyle { frac {m} {100}} = 1- (1 - { frac {1} {N}}) ^ { frac {nN} {100}}}$ Для больших значений ${ displaystyle N}$, предположение, которое может быть разумно сделано для типичных белков, это выражение примерно равно ${ displaystyle { frac {m} {100}} = 1-e ^ {- { frac {n} {100}}}}$

Достоверность этих оценок можно проверить, подсчитав количество аминокислот, которые остаются неизменными под действием матрицы. ${ displaystyle M}$. Общее количество неизмененных аминокислот за временной интервал PAM_п матрица

${ Displaystyle сумма _ {j = 1} ^ {20} n (j) M ^ {n} (j, j)}$

и поэтому доля неизмененных аминокислот составляет

${ displaystyle { frac { sum _ {j = 1} ^ {20} n (j) M ^ {n} (j, j)} {N}} = sum _ {j = 1} ^ {20 } f (j) M ^ {n} (j, j) = 1 - { frac {m} {100}}}$

Пример - PAM250

PAM250 - это обычно используемая матрица оценок для сравнения последовательностей. Требуется вычислить только нижнюю половину матрицы, поскольку по своему построению матрицы PAM должны быть симметричными. Каждая из 20 аминокислот показана сверху и сбоку матрицы с 3 дополнительными неоднозначные аминокислоты. Чаще всего аминокислоты перечислены в алфавитном порядке или перечислены в группах. Эти группы являются характеристиками, общими для аминокислот.^[7]

Матрица PAM250 с заполненными обеими половинами.

Использование в биоинформатике

Определение времени дивергенции в филогенетических деревьях

В гипотеза молекулярных часов предсказывает, что скорость замены аминокислот в конкретном белке будет примерно постоянной во времени, хотя эта скорость может варьироваться в зависимости от семейства белков.^[13] Это говорит о том, что количество мутаций на аминокислоту в белке увеличивается примерно линейно со временем.

Определение времени, когда два белка разошлись, является важной задачей в филогенетика. Летописи окаменелостей часто используются для определения положения событий на временной шкале эволюционной истории Земли, но применение этого источника ограничено. Однако, если известна скорость, с которой тикают молекулярные часы белкового семейства, то есть скорость, с которой увеличивается количество мутаций на аминокислоту, то знание этого количества мутаций позволит определить дату расхождения.

Предположим, что ищется дата расхождения двух родственных белков, взятых из организмов, живущих сегодня. Оба белка накапливали принятые мутации с момента расхождения, поэтому общее количество мутаций на одну аминокислоту, разделяющую их, примерно вдвое превышает то, что отделяет их от их общий предок. Если диапазон матриц PAM используется для выравнивания двух белков, о которых известно, что они связаны, то значение ${ displaystyle n}$ в PAM_п матрица, которая дает лучший результат, скорее всего, соответствует мутациям на аминокислоту, разделяющую два белка. Уменьшение вдвое этого значения и деление на скорость, с которой принятые мутации накапливаются в семействе белков, дает оценку времени отклонения этих двух белков от их общего предка. То есть время расхождения в мир является^[13]

${ displaystyle T = { frac {K} {2r}}}$

Где ${ displaystyle K}$ - количество мутаций на аминокислоту, и ${ displaystyle r}$ - это скорость накопления принятых мутаций в мутациях на аминокислотный сайт за миллион лет.

Использование в BLAST

Матрицы PAM также используются в качестве оценочной матрицы при сравнении последовательностей ДНК или белковых последовательностей для оценки качества выравнивания. Эта форма системы подсчета очков используется в широком спектре программного обеспечения для выравнивания, включая ВЗРЫВ.^[15]

Сравнение PAM и BLOSUM

Хотя матрицы логарифмических шансов PAM были первыми оценочными матрицами, используемыми с BLAST, матрицы PAM. были в значительной степени заменены BLOSUM матрицы. Хотя обе матрицы дают одинаковые результаты оценки, они были созданы с использованием разных методологий. Матрицы BLOSUM были созданы непосредственно из аминокислотных различий в выровненных блоках, которые разошлись в разной степени, матрицы PAM отражают экстраполяция эволюционной информации, основанной на тесно связанных последовательностях, в более длительных временных масштабах.^[16] С момента оценки информации для матриц PAM и BLOSUM. были созданы очень разными способами; числа, связанные с матрицами, имеют принципиально разное значение; числа для матриц PAM увеличиваются для сравнения между более расходящимися белками, тогда как числа для матриц BLOSUM уменьшаются.^[17] Однако все матрицы аминокислотных замен можно сравнить в рамках теоретической информации.^[18] используя их относительную энтропию.

Смотрите также

• Точечная мутация
• Выравнивание последовательности
• Маргарет Дейхофф
• Молекулярные часы
• BLOSUM
• ВЗРЫВ

Рекомендации

внешняя ссылка

• http://www.inf.ethz.ch/personal/gonnet/DarwinManual/node148.html
• http://www.bioinformatics.nl/tools/pam.html Для быстрого расчета матрицы PAM.
• http://web.expasy.org/docs/relnotes/relstat.html Самая свежая статистика из базы знаний Swiss-Prot по белкам. Раздел 6.1 содержит самые последние частоты аминокислот.