WikiDer > Количественная генетика
| Часть серия на |
| Генетика |
|---|
 |
| Ключевые компоненты |
| История и темы |
| Исследование |
| Персонализированная медицина |
| Персонализированная медицина |
Количественная генетика имеет дело с фенотипы которые непрерывно меняются (по таким признакам, как рост или масса) - в отличие от дискретно идентифицируемых фенотипов и генных продуктов (таких как цвет глаз или присутствие определенного биохимического вещества).
Обе ветви используют частоты разных аллели из ген в племенных популяциях (гамодемы), и объединить их с концепциями из простых Менделирующее наследование для анализа моделей наследования между поколениями и потомками. Пока популяционная генетика может сосредоточиться на конкретных генах и продуктах их последующего метаболизма, количественная генетика больше фокусируется на внешних фенотипах и сводит только итоги лежащей в основе генетики.
Из-за непрерывного распределения фенотипических значений количественная генетика должна использовать многие другие статистические методы (такие как размер эффекта, то иметь в виду и отклонение) для привязки фенотипов (атрибутов) к генотипам. Некоторые фенотипы могут быть проанализированы либо как дискретные категории, либо как непрерывные фенотипы, в зависимости от определения точек отсечения или от метрика используется для их количественной оценки.[1]:27–69 Сам Мендель должен был обсудить этот вопрос в своей знаменитой статье:[2] особенно в отношении его атрибута горох высокий / карликовый, которая на самом деле была «длиной стержня».[3][4] Анализ локусы количественных признаков, или QTL,[5][6][7] является более недавним дополнением к количественной генетике, напрямую связывая его с молекулярная генетика.
Генные эффекты
В диплоид организмов, средний генотипический «значение» (значение локуса) может определяться «эффектом» аллеля вместе с господство эффект, а также то, как гены взаимодействуют с генами в других локусах (эпистаз). Основоположник количественной генетики - Сэр Рональд Фишер - многое понял из этого, когда предложил первую математику этого раздела генетики.[8]
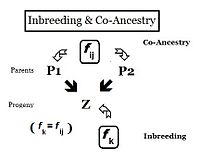
Будучи статистиком, он определил эффекты генов как отклонения от центрального значения, что позволило использовать такие статистические концепции, как среднее значение и дисперсия, которые используют эту идею.[9] Центральное значение, которое он выбрал для гена, было серединой между двумя противоположными гомозиготами в одном локусе. Отклонение оттуда к «большему» гомозиготному генотипу можно назвать «+ а"; и поэтому это"-а«от той же средней точки к« меньшему »генотипу гомозиготы. Это« аллельный »эффект, упомянутый выше. Отклонение гетерозиготы от той же средней точки можно назвать«d", что является эффектом" доминирования ", упомянутым выше.[10] Схема изображает идею. Однако на самом деле мы измеряем фенотипы, и рисунок также показывает, как наблюдаемые фенотипы соотносятся с эффектами генов. Формальные определения этих эффектов признают этот фенотипический фокус.[11][12] Эпистаз статистически рассматривался как взаимодействие (т. Е. Несоответствие),[13] но эпигенетика предполагает, что может потребоваться новый подход.
Если 0<d<а, доминирование рассматривается как частичный или же неполный-пока d=а указывает полный или классический доминирование. Ранее, d>а был известен как «доминирование».[14]
Атрибут гороха Менделя «длина стебля» дает нам хороший пример.[3] Мендель заявил, что у высоких чистопородных родителей длина стебля составляла 6–7 футов (183–213 см), что в среднем составляет 198 см (= P1). У коротких родителей длина стебля составляла от 0,75 до 1,25 фута (23-46 см), с закругленной срединой 34 см (= P2). Их гибрид имел длину от 6 до 7,5 футов (183–229 см) со средним значением 206 см (= F1). Среднее значение P1 и P2 составляет 116 см, что является фенотипическим значением средней точки гомозигот (mp). Аллель влияет на (а) составляет [P1-mp] = 82 см = - [P2-mp]. Эффект доминирования (d) составляет [F1-mp] = 90 см.[15] Этот исторический пример ясно показывает, как связаны значения фенотипа и эффекты генов.
Частоты аллелей и генотипов
Чтобы получить средние значения, дисперсии и другую статистику, оба количество и их происшествия необходимы. Эффекты генов (см. Выше) обеспечивают основу для количество: и частоты контрастных аллелей в пуле гамет оплодотворения предоставляют информацию о происшествия.
Как правило, частота аллеля, вызывающего «большее» в фенотипе (включая доминирование), обозначается символом п, а частота контрастирующего аллеля равна q. Первоначальное предположение, сделанное при создании алгебры, заключалось в том, что родительская популяция была бесконечным и случайным спариванием, которое было сделано просто для облегчения вывода. Последующее математическое развитие также подразумевало, что частотное распределение внутри эффективного пула гамет было однородным: не было локальных возмущений, где п и q разнообразный. Глядя на схематический анализ полового размножения, это то же самое, что заявлять, что пп = пграмм = п; и аналогично для q.[14] Эта система спаривания, основанная на этих предположениях, стала известна как «панмиксия».
Панмиксия в природе встречается редко,[16]:152–180[17] поскольку распределение гамет может быть ограничено, например, ограничениями на распространение или поведением, или случайным отбором образцов (те локальные возмущения, упомянутые выше). Хорошо известно, что в Природе происходит огромная потеря гамет, поэтому диаграмма изображает потенциал гамет-пул отдельно от действительный гамет-пул. Только последний устанавливает окончательные частоты для зигот: это настоящая «гамодема» («гамо» относится к гаметам, а «дема» происходит от греческого «популяция»). Но, согласно предположениям Фишера, гамодем может быть эффективно расширен до потенциал пул гамет, и даже обратно к родительской базовой популяции («исходной» популяции). Случайная выборка, возникающая, когда небольшие «фактические» пулы гамет отбираются из большого «потенциального» пула гамет, известна как генетический дрейф, и рассматривается в дальнейшем.
Хотя панмиксия не может быть широко распространена, потенциал поскольку это действительно происходит, хотя может быть лишь эфемерным из-за этих местных возмущений. Было показано, например, что F2 получено из случайное оплодотворение особей F1 (ан аллогамный F2) после гибридизации является источник нового потенциально панмиктическое население.[18][19] Также было показано, что если панмиктическое случайное оплодотворение происходило постоянно, оно сохраняло бы одни и те же частоты аллелей и генотипов в каждом последующем панмиктическом половом поколении - это и есть Харди Вайнберг равновесие.[13]:34–39[20][21][22][23] Однако, как только генетический дрейф будет инициирован локальной случайной выборкой гамет, равновесие прекратится.
Случайное оплодотворение
Считается, что мужские и женские гаметы в фактическом пуле оплодотворения имеют одинаковую частоту соответствующих аллелей. (Были рассмотрены исключения.) Это означает, что когда п мужские гаметы, несущие А аллель беспорядочно оплодотворять п женские гаметы, несущие тот же аллель, полученная зигота имеет генотип AA, а при случайном оплодотворении комбинация встречается с частотой п Икс п (= п2). Точно так же зигота аа происходит с частотой q2. Гетерозиготы (Аа) может возникнуть двумя способами: когда п мужчина (А аллель) беспорядочно оплодотворять q женский (а аллель) гаметы и наоборот. Таким образом, результирующая частота гетерозиготных зигот равна 2pq.[13]:32 Обратите внимание, что такая популяция никогда не бывает гетерозиготной более чем наполовину, этот максимум наблюдается, когда п=q= 0.5.
Таким образом, при случайном оплодотворении частоты зигот (генотипов) являются квадратичным разложением гаметических (аллельных) частот: . («= 1» означает, что частоты даны в дробной форме, а не в процентах; и что в предложенной структуре нет никаких пропусков.)
Обратите внимание, что «случайное оплодотворение» и «панмиксия» нет синонимы.
Исследовательский крест Менделя - контраст
Эксперименты Менделя с горохом были построены путем установления истинных родителей с «противоположными» фенотипами по каждому признаку.[3] Это означало, что каждый противоположный родитель был гомозиготным только по своему соответствующему аллелю. В нашем примере "высокий против карлик ", высокий родитель будет генотипом TT с п = 1 (и q = 0); в то время как карликовый родитель будет генотипом тт с q = 1 (и п = 0). После контролируемого скрещивания их гибрид Тт, с п = q = ½. Однако частота этой гетерозиготы = 1, потому что это F1 искусственного скрещивания: он не возник в результате случайного оплодотворения.[24] Поколение F2 было произведено путем естественного самоопыления F1 (с контролем за заражением насекомыми), в результате чего п = q = ½ поддерживается. Такой F2 называется «автогамным». Однако частота генотипов (0,25 TT, 0.5 Тт, 0.25 тт) возникли из-за системы спаривания, очень отличной от случайного оплодотворения, поэтому квадратичное разложение избегалось. Полученные числовые значения были такими же, как и для случайного оплодотворения, только потому, что это частный случай первоначального скрещивания гомозиготных противоположных родителей.[25] Мы можем заметить, что из-за преобладания Т- [частота (0,25 + 0,5)] больше тт [частота 0,25], соотношение 3: 1 сохраняется.
Такое скрещивание, как скрещивание по Менделю, где истинно племенные (в основном гомозиготные) противоположные родители скрещиваются контролируемым образом с получением F1, является частным случаем гибридной структуры. F1 часто рассматривается как «полностью гетерозиготный» по рассматриваемому гену. Однако это чрезмерное упрощение и не применяется в целом - например, когда отдельные родители не гомозиготны или когда население скрещиваться с образованием гибридные рои.[24] Общие свойства внутривидовых гибридов (F1) и F2 (как «автогамных», так и «аллогамных») рассматриваются в следующем разделе.
Самооплодотворение - альтернатива
Заметив, что горох является естественным самоопыляемым, мы не можем продолжать использовать его в качестве примера для иллюстрации свойств случайного оплодотворения. Самооплодотворение («самоопыление») - основная альтернатива случайному оплодотворению, особенно внутри растений. Большинство зерновых культур Земли самоопыляются естественным путем (например, рис, пшеница, ячмень), а также бобовые. Учитывая миллионы особей каждого из них на Земле в любое время, очевидно, что самооплодотворение не менее важно, чем случайное оплодотворение. Самооплодотворение - наиболее интенсивная форма инбридинг, который возникает всякий раз, когда существует ограниченная независимость генетического происхождения гамет. Такое снижение независимости возникает, если родители уже являются родственниками и / или из-за генетического дрейфа или других пространственных ограничений на распространение гамет. Анализ пути показывает, что это одно и то же.[26][27] Исходя из этого, коэффициент инбридинга (часто обозначается как F или же ж) количественно оценивает влияние инбридинга по любой причине. Есть несколько формальных определений ж, и некоторые из них рассматриваются в следующих разделах. А пока отметим, что для многолетнего самооплодотворяющегося вида ж = 1.Природные самооплодотворяющиеся популяции не единичны » чистые линии ", однако, представляют собой смеси таких линий. Это становится особенно очевидным при одновременном рассмотрении более чем одного гена. Поэтому частоты аллелей (п и q) Кроме как 1 или же 0 все еще актуальны в этих случаях (вернитесь к разделу Менделя). Однако частоты генотипов принимают другую форму.
В целом частоты генотипов становятся за AA и за Аа и за аа.[13]:65
Обратите внимание, что частота гетерозигот снижается пропорционально ж. Когда ж = 1эти три частоты становятся соответственно п, 0 и q И наоборот, когда f = 0, они сводятся к квадратичному разложению случайного удобрения, показанному ранее.
Средняя численность населения
Среднее значение популяции смещает центральную контрольную точку от средней точки гомозиготы (mp) к среднему значению для популяции, воспроизводящейся половым путем. Это важно не только для переноса фокуса в мир природы, но и для того, чтобы основная тенденция Используется статистикой / биометрией. В частности, квадрат этого среднего - это поправочный коэффициент, который позже используется для получения генотипических дисперсий.[9]
В свою очередь, для каждого генотипа его аллельный эффект умножается на его частоту генотипа; и продукты накапливаются по всем генотипам в модели. Чтобы получить сжатый результат, обычно следует некоторое алгебраическое упрощение.
Среднее значение после случайного оплодотворения
Вклад AA является , что из Аа является , и что из аа является . Собирая вместе двух а сроки и накапливая все, результат: . Упрощение достигается за счет того, что , и напоминая, что , тем самым сводя правый член к .
Таким образом, краткий результат .[14] :110
Это определяет среднее значение популяции как «смещение» от средней точки гомозиготы (вспомните а и d определяются как отклонения с этой середины). На рисунке изображены грамм по всем значениям п для нескольких значений d, включая один случай небольшого доминирования. Заметь грамм часто бывает отрицательным, тем самым подчеркивая, что это само по себе отклонение (из mp).
Наконец, чтобы получить действительный Среднее значение популяции в "фенотипическом пространстве", к этому смещению добавляется среднее значение: .
Примером могут служить данные о длине колоса кукурузы.[28]:103 Если предположить, что представлен только один ген, а = 5,45 см, d = 0,12 см [фактически "0"], mp = 12,05 см. Далее предполагая, что п = 0,6 и q = 0,4 в этом примере совокупности, тогда:
грамм = 5.45 (0.6 − 0.4) + (0.48)0.12 = 1,15 см (округлено); и
п = 1.15 + 12.05 = 13.20 см (округлено).
Среднее значение после длительного самооплодотворения
Вклад AA является , в то время как аа является . [См. Частоты выше.] Собираем этих двух а условия вместе приводят к очень простому конечному результату:
. Как прежде, .
Часто "G(f = 1)"сокращенно" G1".
Горох Менделя может предоставить нам эффекты аллелей и среднюю точку (см. Ранее); и смешанная самоопыляемая популяция с п = 0,6 и q = 0,4 представляет собой пример частот. Таким образом:
грамм(f = 1) = 82 (0,6 - 0,04) = 59,6 см (округлено); и
п(f = 1) = 59,6 + 116 = 175,6 см (округлено).
Среднее - общее оплодотворение
Общая формула включает коэффициент инбридинга ж, а затем может приспособиться к любой ситуации. Процедура точно такая же, как и раньше, с использованием взвешенных частот генотипов, приведенных ранее. После перевода на наши символы и дальнейшей перестановки:[13] :77–78
Предположим, что пример кукурузы [приведенный ранее] был ограничен холмом (узким прибрежным лугом) и имел частичное инбридинг до степени ж = 0.25, затем, используя третью версию (см. выше) граммж:
грамм0.25 = 1,15 - 0,25 (0,48) 0,12 = 1,136 см (округлено), с п0.25 = 13,194 см (округлено).
В этом примере практически отсутствует какой-либо эффект от инбридинга, потому что практически не было доминирования этого признака (d → 0). Рассмотрение всех трех версий граммж показывает, что это приведет к незначительному изменению среднего значения по совокупности. Однако там, где доминирование было заметным, произошли значительные изменения.
Генетический дрейф
Генетический дрейф был представлен при обсуждении вероятности того, что панмиксия широко распространена как естественный образец оплодотворения. [См. Раздел о частотах аллелей и генотипов.] Здесь выборка гамет из потенциал gamodeme обсуждается более подробно. Выборка включает случайное оплодотворение между парами случайных гамет, каждая из которых может содержать либо А или а аллель. Таким образом, выборка является биномиальной.[13]:382–395[14]:49–63[29]:35[30]:55 Каждый «пакет» выборки включает 2N аллели, и производит N зиготы («потомство» или «линия») в результате. В течение репродуктивного периода этот отбор образцов повторяется снова и снова, так что конечный результат представляет собой смесь образцов потомства. Результат дисперсное случайное удобрение Эти события и общий конечный результат рассматриваются здесь на иллюстративном примере.
"Базовые" частоты аллелей в примере соответствуют частотам потенциальный гамодем: частота А является пграмм = 0.75, а частота а является qграмм = 0.25. [белая этикетка "1"на диаграмме.] Пять примеров реальных гамодемов биномиально отбираются из этой базы (s = количество образцов = 5), и каждый образец обозначается «индексом» k: с к = 1 .... с последовательно. (Это "пакеты" отбора проб, упомянутые в предыдущем абзаце.) Количество гамет, участвующих в оплодотворении, варьируется от образца к образцу и выражается как 2Nk [в белая этикетка "2"на диаграмме]. Всего (Σ) отобранных гамет всего 52 [белая этикетка "3"на диаграмме]. Поскольку каждый образец имеет свой размер, веса необходимы для получения средних значений (и другой статистики) при получении общих результатов. Это , и даны в белая этикетка "4"на диаграмме.
Примерные гамодемы - генетический дрейф
После завершения этих пяти событий биномиальной выборки полученные фактические гамодемы содержали разные частоты аллелей - (пk и qk). [Они приведены в белая этикетка "5"на диаграмме.] Этот результат на самом деле является генетическим дрейфом. Обратите внимание, что два образца (k = 1 и 5) имеют те же частоты, что и основание (потенциал) гамодем. Другой (k = 3) имеет п и q "перевернутый". Выборка (k = 2) оказывается "крайним" случаем, когда пk = 0.9 и qk = 0.1 ; в то время как оставшийся образец (k = 4) находится в «середине диапазона» частот его аллелей. Все эти результаты возникли только «случайно», благодаря биномиальной выборке. Однако, возникнув, они установили все последующие свойства потомства.
Поскольку выборка предполагает случайность, вероятности ( ∫k ) получения каждого из этих образцов. Эти биномиальные вероятности зависят от начальных частот (пграмм и qграмм) и размер выборки (2Nk). Их утомительно получить,[13]:382–395[30]:55 но представляют значительный интерес. [Видеть белая этикетка "6"на диаграмме.] Два образца (k = 1, 5) с частотами аллелей, такими же, как в потенциальный гамодем, имели более высокие «шансы» на появление, чем другие образцы. Однако их биномиальные вероятности различались из-за разного размера выборки (2Nk). Образец «разворота» (k = 3) имел очень низкую вероятность возникновения, что, возможно, подтверждает то, чего можно было ожидать. Однако гамодема «экстремальной» частоты аллеля (k = 2) не была «редкой»; и образец "среднего диапазона" (k = 4) был редкий. Те же самые вероятности применимы также к потомству этих оплодотворений.
Здесь некоторые подведение итогов можно начинать. В общие частоты аллелей в основной массе потомства представлены средневзвешенными значениями соответствующих частот отдельных выборок. То есть: и . (Заметь k заменяется на • для общего результата - обычная практика.)[9] Результаты для примера: п• = 0,631 и q• = 0.369 [черная метка "5"на диаграмме]. Эти значения существенно отличаются от исходных (пграмм и qграмм) [белая этикетка "1"]. Частоты аллелей в выборке также имеют дисперсию, а также среднее значение. Это было получено с использованием сумма квадратов (СС) метод [31] [См. Справа от черная метка "5"на диаграмме]. [Дальнейшее обсуждение этой вариации происходит в разделе ниже, посвященном обширному генетическому дрейфу.]
Линии потомства - дисперсия
В частоты генотипов из пяти выборок потомства получены из обычного квадратичного разложения их соответствующих частот аллелей (случайное оплодотворение). Результаты представлены на диаграммах. белая этикетка "7"для гомозигот, а при белая этикетка "8"для гетерозигот. Подобная перестановка подготавливает почву для мониторинга уровней инбридинга. Это можно сделать либо путем изучения уровня общий гомозиготный [(п2k + q2k) = (1 - 2пkqk)], или исследуя уровень гетерозиготности (2pkqk), поскольку они дополняют друг друга.[32] Обратите внимание, что образцы к = 1, 3, 5 все имели одинаковый уровень гетерозиготности, несмотря на то, что один был «зеркальным отображением» других в отношении частот аллелей. «Крайний» случай частоты аллелей (k = 2) имел наибольший гомозиготный (наименьший гетерозиготный) из всех образцов. Случай "среднего диапазона" (k = 4) имели наименьшую гомозиготность (наибольшую гетерозиготность): фактически каждый из них был равен 0,50.
В Общая сводка можно продолжить, получив средневзвешенное частот соответствующих генотипов для основной массы потомства. Таким образом, для AA, это , за Аа , это и для аа, это . Результаты примера приведены на черная метка "7"для гомозигот, а при черная метка "8"для гетерозиготы. Обратите внимание, что среднее значение гетерозиготности 0.3588, который в следующем разделе используется для изучения инбридинга в результате этого генетического дрейфа.
Следующим предметом интереса является сама дисперсия, которая относится к «рассредоточению» потомства ». население означает. Они получены как [см. раздел, посвященный среднему значению популяции], по очереди для каждого образца потомства, используя примеры эффектов генов, приведенные на белая этикетка "9"на диаграмме. Затем каждый получается также [при белая этикетка "10"на диаграмме]. Обратите внимание, что" лучшая "линия (k = 2) имела наибольший частота аллеля для "большего" аллеля (А) (он также имел самый высокий уровень гомозиготности). В наихудший потомство (k = 3) имело самую высокую частоту «меньшего» аллеля (а), что и объясняет его низкую производительность. Эта «плохая» линия была менее гомозиготной, чем «лучшая» линия; и он имел тот же уровень гомозиготности, что и два второе место линии (k = 1, 5). Линия потомства с аллелями «больше» и «меньше», присутствующими с одинаковой частотой (k = 4), имела среднее значение ниже общее среднее (см. следующий абзац) и имели самый низкий уровень гомозиготности. Эти результаты показывают тот факт, что аллели, наиболее распространенные в «генофонде» (также называемом «зародышевой плазмой»), определяют производительность, а не уровень гомозиготности как таковой. Только биномиальная выборка влияет на эту дисперсию.
В Общая сводка теперь можно заключить, получив и . Пример результата для п• составляет 36,94 (черная метка "10"на диаграмме). Это позже используется для количественной оценки инбридинговая депрессия в целом по выборке гамет. [См. Следующий раздел.] Однако напомним, что некоторые «недепрессивные» средства потомства уже идентифицированы (k = 1, 2, 5). Это загадка инбридинга - хотя в целом может наблюдаться «депрессия», обычно среди выборок гамодем есть превосходящие линии.
Эквивалент постдисперсионного панмиктика - инбридинг
Включено в Общая сводка были средние частоты аллелей в смеси линий потомства (п• и q•). Теперь их можно использовать для построения гипотетического панмиктического эквивалента.[13]:382–395[14]:49–63[29]:35 Это можно рассматривать как «эталон» для оценки изменений, вызванных выборкой гамет. Пример добавляет такую панмиктику справа от диаграммы. Частота AA следовательно является (п•)2 = 0,3979. Это меньше, чем в дисперсном объеме (0,4513 ат. черная метка "7"). Аналогично для аа, (q•)2 = 0,1303 - снова меньше эквивалента в основной массе потомства (0,1898). Четко, генетический дрейф повысил общий уровень гомозиготности на величину (0,6411 - 0,5342) = 0,1069. В дополнительном подходе вместо этого может использоваться гетерозиготность. Панмиктический эквивалент для Аа является 2 шт.• q• = 0,4658, что составляет выше чем в отобранном объеме (0,3588) [черная метка "8"]. Выборка привела к снижению гетерозиготности на 0,1070, что тривиально отличается от более ранней оценки из-за ошибок округления.
В коэффициент инбридинга (ж) был представлен в раннем разделе о самооплодотворении. Здесь рассматривается формальное определение: ж вероятность того, что два «одинаковых» аллеля (то есть А и А, или же а и а), которые оплодотворяют вместе, имеют общее наследственное происхождение - или (более формально) ж это вероятность того, что два гомологичных аллеля являются аутозиготными.[14][27] Рассмотрим любую случайную гамету в потенциал гамодема, у которой партнер по сингамии ограничен биномиальной выборкой. Вероятность того, что вторая гамета является аутозиготной по отношению к первой, равна 1 / (2N), величина, обратная размеру гамодема. Для пяти примеров потомства эти количества равны 0,1, 0,0833, 0,1, 0,0833 и 0,125 соответственно, а их средневзвешенное значение равно 0.0961. Это коэффициент инбридинга основной массы примерного потомства, при условии, что это беспристрастный относительно полного биномиального распределения. Пример, основанный на s = 5 однако, вероятно, будет предвзятым по сравнению с соответствующим полным биномиальным распределением, основанным на номере выборки (s) приближение к бесконечности (s → ∞). Другое производное определение ж для полного распространения заключается в том, что ж также равняется увеличению гомозиготности, что равняется падению гетерозиготности.[33] Например, эти изменения частоты 0.1069 и 0.1070, соответственно. Этот результат отличается от приведенного выше, указывая на то, что в примере присутствует систематическая ошибка относительно полного базового распределения. Для примера сам, эти последние значения лучше использовать, а именно ж• = 0.10695.
В Средняя численность населения эквивалентного панмиктика находится как [а (п•-q•) + 2 п.•q• d] + mp. На примере генные эффекты (белая этикетка "9"на диаграмме), это среднее значение 37,87. Эквивалентное среднее значение в дисперсном объеме составляет 36,94 (черная метка "10"), что подавлено суммой 0.93. Это инбридинговая депрессия от этого генетического дрейфа. Однако, как отмечалось ранее, три потомства были нет в депрессии (k = 1, 2, 5) и имел средства даже больше, чем у панмиктического эквивалента. Это те линии, которые селекционер ищет в программе выбора линий.[34]
Обширная биномиальная выборка - восстановлена ли панмиксия?
Если количество биномиальных отсчетов велико (s → ∞ ), тогда п• → пграмм и q• → qграмм. Можно спросить, действительно ли панмиксия вновь появится при таких обстоятельствах. Тем не менее выборка частот аллелей имеет все еще произошло, в результате чего σ2р, д ≠ 0.[35] Фактически, как s → ∞, то , какой отклонение из полное биномиальное распределение.[13]:382–395[14]:49–63 Кроме того, «уравнения Валунда» показывают, что основная масса потомков гомозигота частоты можно получить как сумму их соответствующих средних значений (п2• или же q2•) плюс σ2р, д.[13]:382–395 Точно так же основная часть гетерозигота частота (2 шт.• q•) минус дважды в σ2р, д. Разница, возникающая в результате биномиальной выборки, явно присутствует. Таким образом, даже когда s → ∞, потомство-основная масса генотип частоты все еще показывают повышенный гомозиготность, и снижение гетерозиготности, Все еще дисперсия потомства средств, И еще инбридинг и инбридинговая депрессия. То есть панмиксия - это нет повторно достигнутый однажды потерянный из-за генетического дрейфа (биномиальная выборка). Однако новый потенциал панмиксия может быть инициирована через аллогамный F2 после гибридизации.[36]
Продолжающийся генетический дрейф - увеличенная дисперсия и инбридинг
Предыдущее обсуждение генетического дрейфа рассматривало только один цикл (поколение) этого процесса. Когда отбор образцов продолжается в течение последующих поколений, заметные изменения происходят в σ2п, q и ж. Кроме того, необходим еще один «указатель», чтобы отслеживать «время»: т = 1 .... у куда у = количество рассматриваемых "лет" (поколений). Часто используется методика добавления текущего биномиального приращения (Δ = "de novo") к тому, что произошло ранее.[13] Здесь исследуется все биномиальное распределение. [Сокращенный пример не дает никаких дополнительных преимуществ.]
Дисперсия через σ2р, д
Ранее эта дисперсия (σ 2р, д [35]) было замечено как: -
Со временем это также является результатом первый цикл, и так (для краткости). В цикле 2 эта дисперсия снова генерируется - на этот раз становится de novo дисперсия () - и накапливается до того, что уже было - дисперсия «переходящего остатка». В второй вариация цикла () представляет собой взвешенную сумму этих двух компонентов с весами для de novo и = для «переходящего остатка».
Таким образом,
(1)
Расширение для обобщения на любое время т , после значительного упрощения становится:[13]:328-
(2)
Потому что именно эта вариация в частотах аллелей вызвала «разнесение» средств потомства (разброс), изменение σ2т по поколениям указывает на изменение уровня разброс.
Дисперсия через ж
Методика исследования коэффициента инбридинга аналогична той, что используется для σ 2р, д. Те же веса, что и раньше, используются соответственно для de novo f ( Δ f ) [напомним, это 1 / (2N) ] и переходящий остаток f. Следовательно, , что похоже на Уравнение (1) в предыдущем подразделе.
В общем, после перестановки,[13]
Дальнейшие преобразования этого общего уравнения обнаруживают некоторые интересные взаимосвязи.
(А) После некоторого упрощения,[13] . Слева - разница между текущим и предыдущим уровнями инбридинга: изменение инбридинга (δfт). Обратите внимание, что это изменение инбридинга (δfт) равно de novo инбридинг (Δf) только для первого цикла - когда fт-1 является нуль.
(В) Следует отметить (1-ет-1), что является "индексом не-инбридинг". Он известен как панмиктический индекс.[13][14] .
(С) Дальнейшие полезные отношения возникают с участием панмиктический индекс.[13][14]
Самоопыление при случайном оплодотворении
Легко не заметить, что случайное оплодотворение включает самооплодотворение. Сьюэлл Райт показал, что пропорция 1 / N из случайные оплодотворения на самом деле самооплодотворение , с остатком (N-1) / N существование перекрестное оплодотворение . После анализа и упрощения пути новый вид случайное оплодотворение инбридинг оказалось: .[27][37] При дальнейшей перегруппировке были подтверждены более ранние результаты биномиальной выборки вместе с некоторыми новыми схемами. Два из них были потенциально очень полезными, а именно: (А) ; и (В) .
Признание того, что эгоизм может по сути быть частью случайное внесение удобрений приводит к некоторым проблемам с использованием предыдущего случайное оплодотворение «коэффициент инбридинга». Ясно, что это неприемлемо для любого вида, неспособного к самооплодотворение, который включает растения с механизмами самонесовместимости, двудомные растения и бисексуальные животные. Уравнение Райта было изменено позже, чтобы предоставить версию случайного оплодотворения, в которой участвовали только перекрестное оплодотворение без самооплодотворение. Пропорция 1 / N ранее из-за селфи теперь определил переноситься инбридинг с дрейфом генов, возникший в результате предыдущего цикла. Новая версия:[13]:166
На графиках справа показаны различия между стандартными случайное оплодотворение РФ, и случайное оплодотворение с поправкой на «только перекрестное оплодотворение» CF. Как видно, проблема нетривиальна для малых размеров выборки гамодем.
Теперь необходимо отметить, что не только «панмиксия» нет синоним «случайного оплодотворения», но также и «случайное оплодотворение» нет синоним «перекрестного оплодотворения».
Гомозиготность и гетерозиготность
В подразделе «Образцы гамодемов - генетический дрейф» была прослежена серия выборок гамет, результатом которых было увеличение гомозиготности за счет гетерозиготности. С этой точки зрения рост гомозиготности был связан с выборками гамет. Уровни гомозиготности можно также рассматривать в зависимости от того, возникли ли гомозиготы аллозиготно или аутозиготно. Напомним, что аутозиготные аллели имеют одинаковое аллельное происхождение, вероятность (частота) которых является в коэффициент инбридинга (ж) по определению. Пропорция, возникающая аллозиготно следовательно является (1-е). Для А-содержащие гаметы, которые присутствуют с общей частотой п, поэтому общая частота автозиготных случаев составляет (ж п). Аналогично для а-несущие гаметы частота аутозигот составляет (ж q).[38] Эти две точки зрения относительно частот генотипов должны быть связаны, чтобы обеспечить согласованность.
Следуя в первую очередь авто / алло точки зрения, рассмотрим аллозиготный компонент. Это происходит с частотой (1-е), а аллели объединяются по случайное оплодотворение квадратичное разложение. Таким образом:
Во-вторых, отбор проб точка зрения пересматривается. Ранее было отмечено, что снижение гетерозигот было . Это снижение равномерно распространяется на каждую гомозиготу; и добавляется к их основным случайное оплодотворение ожидания. Следовательно, частоты генотипов следующие: для "АА" гомозигота; для "аа" гомозигота; и для гетерозиготы.
В-третьих, последовательность Между двумя предыдущими точками зрения необходимо установить. Сразу становится очевидным [из соответствующих уравнений выше], что частота гетерозигот одинакова в обеих точках зрения. Однако такой простой результат не сразу очевиден для гомозигот. Начнем с рассмотрения AA окончательное уравнение гомозиготы в авто / алло абзац выше: - . Раскройте скобки и соберите [в полученном результате] два новых члена с общим множителем. ж в них. Результат: . Затем для заключенного в скобки " п20 ", а (1-кв) заменяется на п, результат становится . После этой замены становится простым делом умножения, упрощения и наблюдения за знаками. Конечный результат , что и является результатом для AA в отбор проб пункт. Таким образом, две точки зрения последовательный для AA гомозигота. Подобным образом, последовательность аа точки обзора также могут быть показаны. Эти две точки зрения совпадают для всех классов генотипов.
Расширенные принципы
Другие способы оплодотворения
В предыдущих разделах дисперсионное случайное внесение удобрений (генетический дрейф) был рассмотрен всесторонне, а самооплодотворение и гибридизация были изучены в различной степени. На диаграмме слева изображены первые два из них вместе с другим «пространственным» шаблоном: острова. Это образец случайное оплодотворение с участием дисперсные гамодемы, с добавлением «перекрытий», в которых недисперсионный происходит случайное оплодотворение. С острова узор, индивидуальные размеры гамодем (2N) наблюдаемы и перекрываются (м) минимальны. Это одна из возможностей Сьюэлла Райта.[37] Помимо «пространственных» моделей оплодотворения, существуют и другие, основанные либо на «фенотипических», либо на «родственных» критериях. В фенотипический базы включают ассортативный оплодотворение (между сходными фенотипами) и дезассортативный оплодотворение (между противоположными фенотипами). В отношение шаблоны включают брат пересечения, двоюродный брат пересечения и обратное скрещивание- и рассматриваются в отдельном разделе. Самостоятельное оплодотворение можно рассматривать как с пространственной точки зрения, так и с точки зрения отношений.
«Острова» случайного оплодотворения
Гнездовое население состоит из s маленький дисперсное случайное удобрение гамодемы размера выборки ( k = 1 ... s ) с " перекрывает "пропорции в котором недисперсное случайное удобрение происходит. В дисперсионная доля таким образом . Основная часть населения состоит из средневзвешенные размеров выборки, частот аллелей и генотипов и средних значений потомства, как это было сделано для генетического дрейфа в предыдущем разделе. Однако каждый размер выборки гаметы сокращается, чтобы учесть перекрывает, таким образом находя эффективен для .
Для краткости далее аргументы опускаются. Напомним, что является в целом. [Здесь и далее 2N относится к ранее определенный размер выборки, а не какой-либо версии с поправкой на острова.]
После упрощения[37]
Это Δf также подставляется в предыдущее коэффициент инбридинга чтобы получить [37]
Эффективный доля перекрытия также можно получить,[37] в качестве
Графики справа показывают инбридинг для размера гамодема 2N = 50 за обычное дисперсное случайное удобрение (РФ) (т = 0), и для четыре уровня перекрытия (m = 0,0625, 0,125, 0,25, 0,5) из острова случайное оплодотворение. Действительно, произошло сокращение инбридинга в результате недисперсное случайное удобрение в перекрытиях. Это особенно примечательно как м → 0,50. Сьюэлл Райт предположил, что это значение должно быть пределом для использования этого подхода.[37]
Перемешивание аллелей - замена аллелей
В генная модель исследует путь наследственности с точки зрения «входов» (аллелей / гамет) и «выходов» (генотипов / зигот), при этом оплодотворение является «процессом» преобразования одного в другое. Альтернативная точка зрения концентрируется на самом «процессе» и рассматривает генотипы зигот как результат перетасовки аллелей. В частности, он рассматривает результаты так, как если бы один аллель «заменил» другой во время перетасовки, вместе с остатком, который отклоняется от этой точки зрения. Это составляло неотъемлемую часть метода Фишера,[8] в дополнение к его использованию частот и эффектов для генерации своей генетической статистики.[14] Дискурсивный вывод замена аллеля альтернатива следует.[14]:113
Предположим, что обычное случайное оплодотворение гамет в «базовой» гамодеме, состоящей из п гаметы (А) и q гаметы (а) - заменяется оплодотворением «потоком» гамет, содержащих единственный аллель (А или же а, но не оба). Зиготические результаты можно интерпретировать с точки зрения аллеля "наводнения", "замещающего" альтернативный аллель в лежащей в основе "базовой" гамодеме. Схема помогает понять эту точку зрения: верхняя часть изображает А подстановки, а в нижней части а подмена. («Аллель RF» на диаграмме - это аллель в «базовой» гамодеме.)
Рассмотрим в первую очередь верхнюю часть. Потому что основание А присутствует с частотой п, то заменять А удобряет его с частотой п в результате зигота AA с аллельным эффектом а. Следовательно, его вклад в результат - это продукт . Аналогично, когда заменять удобряет основание а (в результате чего Аа с частотой q и гетерозиготный эффект d) вклад . Общий результат замены на А следовательно является, . Теперь оно ориентировано на среднее значение населения [см. Предыдущий раздел], выражая его как отклонение от этого среднего:
После некоторого алгебраического упрощения это становится
Аналогичное рассуждение можно применить к нижней части диаграммы, обращая внимание на различия в частотах и эффектах генов. В результате эффект замещения из а, который
В последующих разделах эти эффекты замещения помогают определить генотипы генной модели как состоящие из раздела, предсказанного этими новыми эффектами (замена ожидания) и остаток (отклонения замещения) между этими ожиданиями и предыдущими эффектами генной модели. В ожидания также называются племенные ценности а отклонения также называют отклонения доминирования.
В конечном итоге разница, возникающая из-за ожидания замены становится так называемым Аддитивная генетическая дисперсия (σ2А)[14] (так же Общая дисперсия [40]) - тогда как возникающее из отклонения замещения становится так называемым Дисперсия доминирования (σ2D). Примечательно, что ни один из этих терминов не отражает истинное значение этих различий. В «генная дисперсия» менее сомнительно, чем аддитивная генетическая дисперсия, и многое другое в соответствии с собственным названием Фишера для этого раздела.[8][29]:33 Менее вводящее в заблуждение название для отклонения доминирования дисперсия это "квазидоминантная дисперсия" [см. следующие разделы для дальнейшего обсуждения]. Эти последние термины являются здесь предпочтительными.
Новое определение генных эффектов
Эффекты генной модели (а, d и -а) вскоре станут важными при выводе отклонения от замены, которые впервые обсуждались в предыдущем Замена аллелей раздел. Однако их необходимо переопределить, прежде чем они станут полезными в этом упражнении. Во-первых, их необходимо рецентрализовать вокруг среднего населения (грамм), а во-вторых, их необходимо перестроить как функции β, то средний эффект замещения аллелей.
Рассмотрим в первую очередь рецентрализацию. Рецентрализованный эффект для AA является а • = а - G который после упрощения становится а • = 2q(а-пг). Аналогичный эффект для Аа является d • = d - G = a (q-п) + d (1-2pq), после упрощения. Наконец, рецентрализованный эффект для аа является (-a) • = -2п(а +qг).[14]:116–119
Во-вторых, рассмотрите реорганизацию этих рецентрализованных эффектов как функции β. Вспоминая из раздела «Замена аллелей», что β = [a + (q-p) d], перегруппировка дает а = [β - (q-p) d]. После замены этого на а в а • и упрощая, окончательная версия становится а •• = 2q (β-qd). По аналогии, d • становится d •• = β (q-p) + 2pqd; и (-a) • становится (-a) •• = -2p (β + pd).[14]:118
Замена генотипа - ожидания и отклонения
Генотипы зиготы являются целью всего этого препарата. Гомозиготный генотип AA это союз двух эффекты замещения A, по одному от каждого пола. Его ожидание замены следовательно является βAA = 2βА = 2qβ (см. предыдущие разделы). Точно так же ожидание замены из Аа является βАа = βА + βа = (q-п) β ; и для аа, βаа = 2βа = -2пβ. Эти ожидания замены генотипов также называют племенные ценности.[14]:114–116
Замены отклонений различия между этими ожидания и генные эффекты после их двухэтапного переопределения в предыдущем разделе. Следовательно, dAA = a •• - βAA = -2q2d после упрощения. По аналогии, dАа = d •• - βАа = 2pqd после упрощения. Ну наконец то, dаа = (-a) •• - βаа = -2п2d после упрощения.[14]:116–119 Обратите внимание, что все эти отклонения замещения в конечном итоге являются функциями генного эффекта d- что объясняет использование ["d" плюс нижний индекс] в качестве их символов. Однако это серьезный non sequitur логически рассматривать их как объяснение доминирования (гетерозиготности) во всей генной модели: они просто функции "d", а не аудит буквы "d" в системе. Они находятся как получено: отклонения от ожиданий замены!
"Ожидания замещения" в конечном итоге приводят к σ2А (так называемая «аддитивная» генетическая дисперсия); а «замещающие отклонения» порождают σ2D (так называемая генетическая изменчивость "доминирования"). Однако имейте в виду, что средний эффект замещения (β) также содержит «d» [см. Предыдущие разделы], что указывает на то, что доминирование также встроено в «аддитивную» дисперсию [см. Следующие разделы о генотипической дисперсии для их происхождения]. Помните также [см. Предыдущий абзац], что «отклонения замещения» не учитывают доминирование в системе (являясь не чем иным, как отклонениями от ожидания замены), но которые алгебраически состоят из функций от "d". Более подходящие названия для этих соответствующих отклонений могут быть σ2B (дисперсия "Ожидания по разведению") и σ2δ (дисперсия «Отклонения размножения»). Однако, как отмечалось ранее, «Genic» (σ 2А) и «Квазидоминирование» (σ 2D), соответственно, будет предпочтительным в данном случае.
Генотипическая дисперсия
Есть два основных подхода к определению и разделению генотипическая дисперсия. Один основан на эффекты генной модели,[40] в то время как другой основан на эффекты замены генотипа[14] Они алгебраически взаимно конвертируемы друг с другом.[36] В этом разделе основные случайное оплодотворение рассмотрено происхождение, при этом не учитываются эффекты инбридинга и дисперсии. Это будет рассмотрено позже, чтобы прийти к более общему решению. До этого моногенный лечение заменяется мультигенный один, и пока эпистаз решается в свете выводов эпигенетика, генотипическая дисперсия включает только рассматриваемые здесь компоненты.
Генно-модельный подход - Мазер Джинкс Хейман
Удобно следовать биометрическому подходу, основанному на исправлении нескорректированная сумма квадратов (USS) путем вычитания поправочный коэффициент (CF). Поскольку все эффекты были исследованы через частоты, USS может быть получен как сумма произведений частоты каждого генотипа и квадрата его ген-эффект. КФ в данном случае является среднеквадратическим. Результатом является SS, который, опять же из-за использования частот, также сразу становится отклонение.[9]
В , а . В
После частичного упрощения
Здесь, σ2а это гомозигота или же аллельный дисперсия и σ2d это гетерозигота или же господство дисперсия. В отклонения замещения дисперсия (σ2D) тоже присутствует. В (взвешенная_ковариация)объявление[43] в дальнейшем сокращается до " covобъявление ".
Эти компоненты нанесены на график для всех значений п на сопроводительном рисунке. Заметь covобъявление является отрицательный за р> 0,5.
На большинство из этих компонентов влияет изменение центрального фокуса с средняя точка гомозиготы (mp) к Средняя численность населения (грамм), последний является основой Фактор коррекции. В covобъявление и отклонение замещения отклонения - просто артефакты этого сдвига. В аллельный и господство Вариации - это настоящие генетические части исходной генной модели и единственные европейские генетические компоненты. Уже тогда алгебраическая формула для аллельный отклонение обусловлено наличием грамм: это только господство дисперсия (т.е. σ2d ), на которую не влияет сдвиг от mp к грамм.[36] Эти идеи обычно не ценятся.
Дальнейший сбор терминов [в формате Мазера] приводит к , куда . Позже он пригодится в анализе Диаллеля, который представляет собой экспериментальный план для оценки этой генетической статистики.[44]
Если после последней данной перестановки первые три члена объединяются вместе, далее переупорядочиваются и упрощаются, результатом является дисперсия фишеровского ожидание замены.
То есть:
Обратите особое внимание на то, что σ2А не является σ2а. Первый - это ожидания замены дисперсия, а вторая - аллельный дисперсия.[45] Также обратите внимание, что σ2D (в замещение отклонений дисперсия) нет σ2d (в господство дисперсия), и напомним, что это артефакт, возникающий в результате использования грамм для поправочного коэффициента. [См. «Синий абзац» выше.] Теперь это будет называться дисперсией «квазидоминантности».
Также обратите внимание, что σ2D < σ2d («2pq» всегда дробь); и обратите внимание, что (1) σ2D = 2pq σ2d, и что (2) σ2d = σ2D / (2пк). То есть: подтверждено, что σ2D не дает количественной оценки дисперсии доминирования в модели. Это σ2d который делает это. Однако дисперсия доминирования (σ2d) легко оценивается по σ2D если 2pq доступен.
На рисунке эти результаты можно представить как накапливающиеся σ2а, σ2d и covобъявление чтобы получить σ2А, оставив σ2D все еще разделены. Также на рисунке видно, что σ2D < σ2d, как и следовало ожидать из уравнений.
Общий результат (в формате Фишера):
Подход с замещением аллелей - Фишер
Ссылка на несколько предыдущих разделов о замене аллелей показывает, что два основных эффекта: замена генотипа ожидания и отклонения при замене генотипа. Обратите внимание, что каждый из них уже определен как отклонение от случайное оплодотворение Средняя численность населения (грамм). Таким образом, для каждого генотипа по очереди получается произведение частоты и квадрата соответствующего эффекта, которые накапливаются, чтобы непосредственно получить SS и σ2.[46] Подробности следуют.
σ2А = п2 βAA2 + 2pq βАа2 + q2 βаа2, что упрощает σ2А = 2pqβ2- Генная дисперсия.
σ2D = п2 dAA2 + 2pq dАа2 + q dаа2, что упрощает σ2D = (2pq)2 d2- квазидоминантная дисперсия.
Накопив эти результаты, σ2грамм = σ2А + σ2D. Эти компоненты визуализированы на графиках справа. В средняя замена аллеля Эффект также изображен на графике, но символом является «α» (как это часто бывает в цитатах), а не «β» (как используется здесь).
Однако еще раз обратимся к предыдущим дискуссиям об истинном значении и идентичности этих компонентов. Сам Фишер не использовал эти современные термины для своих компонентов. В ожидания замены дисперсию он назвал "генетический" дисперсия; и отклонения замещения дисперсию он считал просто неназванным остаточный между «генотипической» дисперсией (его имя для этого) и его «генетической» дисперсией.[8][29]:33[47][48] [Терминология и происхождение, использованные в этой статье, полностью соответствуют терминологии Фишера.] Термин Мезер для обозначения ожидания дисперсия"генный"[40]- очевидно, происходит от термина Фишера и избегает использования слова «генетический» (которое стало слишком общим в использовании, чтобы иметь ценность в данном контексте). Неясно происхождение современных вводящих в заблуждение терминов «аддитивная» и «доминирующая» дисперсии.
Обратите внимание, что этот подход с заменой аллелей определяет компоненты отдельно, а затем суммирует их для получения окончательной генотипической дисперсии. И наоборот, подход на основе генной модели позволил получить всю ситуацию (компоненты и общую сумму) как одно упражнение. Бонусы, проистекающие из этого, были (а) откровениями о реальной структуре σ2А, и (б) реальные значения и относительные размеры σ2d и σ2D (см. предыдущий подраздел). Также очевидно, что анализ «Мазера» более информативен, и что на его основе всегда можно построить анализ «Фишера». Однако обратное преобразование невозможно, поскольку информация о covобъявление будет отсутствовать.
Дисперсия и генотипическая дисперсия
В разделе о генетическом дрейфе и в других разделах, посвященных инбридингу, основным результатом выборки частоты аллелей стал разброс потомства средств. Этот набор средств имеет свое среднее значение, а также имеет вариацию: межстрочная дисперсия. (Это изменение самого атрибута, а не частоты аллелей.) По мере дальнейшего развития дисперсии в последующих поколениях ожидается, что эта межлинейная дисперсия будет увеличиваться. И наоборот, по мере роста гомозиготности можно ожидать уменьшения дисперсии внутри линий. Поэтому возникает вопрос, меняется ли общая дисперсия - и если да, то в каком направлении. На сегодняшний день эти вопросы представлены с точки зрения генный (σ 2А ) и квазидоминантность (σ 2D ) вариации, а не компоненты генной модели. Это будет сделано и здесь.
Решающий обзорное уравнение исходит от Сьюэлл Райт,[13] :99,130 [37] и это очертание инбредная генотипическая дисперсия на основе средневзвешенное значение его крайних значений, веса квадратичны относительно коэффициент инбридинга . Это уравнение:
куда коэффициент инбридинга, генотипическая дисперсия на f = 0, генотипическая дисперсия на f = 1, среднее значение населения в f = 0, и среднее значение населения в f = 1.
В компонент [в приведенном выше уравнении] указывает на уменьшение дисперсии в линиях потомства. В компонент направлен на увеличение дисперсии между линиями потомства. Наконец, компонент виден (в следующей строке) для адресации квазидоминирование дисперсия.[13] :99 & 130 Эти компоненты могут быть расширены, тем самым раскрывая дополнительную информацию. Таким образом:-
Во-первых, σ2G (0) [в приведенном выше уравнении] был расширен, чтобы показать его два подкомпонента [см. раздел «Генотипическая дисперсия»]. Далее σ2G (1) был преобразован в 4pqa2, и выводится в следующем разделе. Замена третьего компонента - это разница между двумя «крайностями инбридинга» среднего популяции [см. Раздел «Среднее значение популяции»].[36]
Подводя итог: внутри линии компоненты и ; и межстрочный компоненты и .[36]
Перестановка дает следующее:
По аналогии,
Графики слева показывают эти три генные дисперсии вместе с тремя дисперсиями квазидоминантности по всем значениям ж, за р = 0,5 (при котором дисперсия квазидоминантности максимальна). Графики справа показывают Генотипический разбиения дисперсии (являющиеся суммами соответствующих генный и квазидоминирование перегородки), сменяющие более десяти поколений на примере f = 0,10.
Отвечая, во-первых, на заданные в начале вопросы о общие отклонения [в Σ в графиках]: генная дисперсия растет линейно с коэффициент инбридинга, максимизируя вдвое от начального уровня. В квазидоминантная дисперсия снижается со скоростью (1 - f2 ) пока не закончится на нуле. На низких уровнях ж, снижение очень постепенное, но оно ускоряется с повышением уровня ж.
Во-вторых, обратите внимание на другие тенденции. Вероятно, интуитивно понятно, что в пределах линии дисперсия снижается до нуля при продолжении инбридинга, и это очевидно (оба с одинаковой линейной скоростью (1-е) ). В среди линии оба отклонения увеличиваются с инбридингом до f = 0,5, то генная дисперсия в размере 2f, а квазидоминантная дисперсия в размере (f - f2). В f> 0,5Однако тенденции меняются. В среди линии генная дисперсия продолжает линейное увеличение, пока не сравняется с общий генная дисперсия. Но среди линии квазидоминантная дисперсия сейчас снижается в сторону нуль, потому что (f - f2) также снижается с f> 0,5.[36]
Вывод σ2G (1)
Напомним, когда f = 1, гетерозиготность равна нулю, внутрилинейная дисперсия равна нулю, и, таким образом, вся генотипическая дисперсия равна межстрочный дисперсия и истощение дисперсии доминирования. Другими словами, σ2G (1) - это дисперсия между средними значениями полностью инбредных линий. Напомним далее [из раздела «Среднее значение после самооплодотворения»], что такое означает (G1на самом деле) G = а (р-д). Подстановка (1-кв) для п, дает грамм1 = а (1 - 2q) = a - 2aq.[14]:265 Следовательно σ2G (1) это σ2(a-2aq) фактически. Теперь в целом дисперсия разницы (x-y) является [σ2Икс + σ2у - 2 ковраху ].[49]:100[50] :232 Следовательно, σ2G (1) = [σ2а + σ22aq - 2 ковра(a, 2aq) ] . Но а (аллель эффект) и q (аллель частота) находятся независимый- значит, эта ковариация равна нулю. Более того, а является константой от одной строки к другой, поэтому σ2а также равен нулю. Дальше, 2а - другая константа (k), поэтому σ22aq относится к типу σ2k X. В целом дисперсия σ2k X равно k2 σ2Икс.[50]:232 Сложив все это вместе, мы увидим, что σ2(a-2aq) = (2а)2 σ2q. Напомним [из раздела «Продолжение генетического дрейфа»], что σ2q = pq f . С f = 1 здесь, в рамках настоящего вывода, это становится pq 1 (то есть pq), и это подставляется в предыдущее.
Конечный результат: σ2G (1) = σ2(a-2aq) = 4a2 pq = 2 (2pq a2) = 2 σ2а.
Отсюда сразу следует, что ж σ2G (1) = ж 2 σ2а. [Этот последний ж исходит из исходное уравнение Сьюолла Райта : это нет в ж просто установите "1" в выводе, заключенном двумя строками выше.]
Общая дисперсная генная дисперсия - σ2A (f) и βж
Предыдущие разделы показали, что в пределах линии генная дисперсия основан на производный замещения генная дисперсия (σ2А )-но среди линии генная дисперсия основан на генная модель аллельная дисперсия (σ2а ). Эти два нельзя просто сложить, чтобы получить общая генная дисперсия. Один из подходов к устранению этой проблемы заключался в повторном посещении вывода средний эффект замещения аллелей, а для построения версии (β ж ), который учитывает эффекты дисперсии. Ворона и Кимура достигли этого[13] :130–131 используя повторно центрированные аллельные эффекты (a •, d •, (-a) • ) обсуждалось ранее [«Новое определение генных эффектов»]. Однако впоследствии было обнаружено, что это несколько недооценивает общая генная дисперсия, а новый вывод на основе дисперсии привел к усовершенствованной версии.[36]
В изысканный версия: β ж = {a2 + [(1−ж ) / (1 + ж )] 2 (q - p) ad + [(1-ж ) / (1 + ж )] (q - p)2 d2 } (1/2)
Как следствие, σ2A (f) = (1 + ж ) 2pq βж 2 теперь согласен с [(1-f) σ2А (0) + 2f σ2а (0) ] точно.
Полные и разделенные дисперсные дисперсии квазидоминантности
В общая генная дисперсия представляет собой самостоятельный интерес. Но до уточнений Гордона[36] у него было и другое важное применение. Не существовало существующих оценок "рассредоточенного" квазидоминирования. Это было оценено как разница между оценками Сьюэлла Райта. инбредная генотипическая дисперсия [37] и общая «рассредоточенная» генная дисперсия [см. предыдущий подраздел]. Однако возникла аномалия, потому что общая дисперсия квазидоминантности по-видимому, увеличивалось в раннем инбридинге, несмотря на снижение гетерозиготности.[14] :128 :266
Усовершенствования в предыдущем подразделе исправили эту аномалию.[36] В то же время прямое решение для общая дисперсия квазидоминантности был получен, таким образом избегая необходимости в методе «вычитания», который использовался ранее. Кроме того, прямые решения для межстрочный и внутри линии перегородки квазидоминантная дисперсия были получены также впервые. [Они были представлены в разделе «Дисперсия и генотипическая дисперсия».]
Экологическая дисперсия
Изменчивость окружающей среды - это фенотипическая изменчивость, которую нельзя приписать генетике.Это звучит просто, но экспериментальный план, необходимый для разделения этих двух элементов, требует очень тщательного планирования. Даже «внешнюю» среду можно разделить на пространственную и временную составляющие («Сайты» и «Годы»); или на такие разделы, как «мусор» или «семья», и «культура» или «история». Эти компоненты очень зависят от реальной экспериментальной модели, используемой для проведения исследования. Такие вопросы очень важны при проведении самого исследования, но в этой статье о количественной генетике этого обзора может хватить.
Однако это подходящее место для резюме:
Фенотипическая дисперсия = генотипическая дисперсия + экологическая дисперсия + взаимодействие генотипа с окружающей средой + экспериментальная "ошибка" дисперсия
т.е. σ²п = σ²грамм + σ²E + σ²GE + σ²
или же σ²п = σ²А + σ²D + σ²я + σ²E + σ²GE + σ²
после разделения генотипической дисперсии (G) на составляющие дисперсии «генная» (A), «квазидоминантность» (D) и «эпистатическая» (I).[51]
Вариативность среды появится в других разделах, таких как «Наследуемость» и «Коррелированные атрибуты».
Наследственность и повторяемость
В наследственность признака - доля общей (фенотипической) дисперсии (σ2 п), что связано с генетической дисперсией, будь то полная генотипическая дисперсия или какой-то ее компонент. Он количественно определяет степень, в которой фенотипическая изменчивость обусловлена генетикой: но точное значение зависит от того, какой раздел генетической дисперсии используется в числителе пропорции.[52] Исследовательские оценки наследуемости имеют стандартные ошибки, как и все оценочные статистические данные.[53]
Где дисперсия числителя - это полная генотипическая дисперсия ( σ2грамм) наследственность известна как "широкая" наследственность (ЧАС2). Он количественно определяет степень, в которой изменчивость атрибута определяется генетикой в целом.
Если только общая дисперсия (σ2А) используется в числителе, наследуемость можно назвать "узким смыслом" (h2). Он количественно определяет степень, в которой фенотипическая дисперсия определяется методом Фишера. ожидания замены дисперсия.
Напоминая, что аллельный дисперсия (σ 2а) и господство дисперсия (σ 2d) являются ес-генетическими компонентами генной модели [см. раздел о генотипической дисперсии], и что σ 2D (в отклонения замещения или же "квазидоминирование" дисперсия) и covобъявление обусловлены изменением от середины гомозиготы (mp) к среднему значению (грамм), можно видеть, что истинное значение этих наследуемостей неясно. Наследственность и имеют однозначный смысл.
Узкая наследственность также использовалась для общего прогнозирования результатов искусственный отбор. В последнем случае, однако, более подходящей может быть широкая наследуемость, поскольку изменяется весь атрибут, а не только адаптивная способность. Как правило, продвижение от отбора тем быстрее, чем выше наследуемость. [См. Раздел «Селекция».] У животных наследуемость репродуктивных признаков обычно низкая, в то время как наследуемость устойчивости к болезням и продуктивности умеренно низкая или умеренная, а наследуемость телосложения высокая.
Повторяемость (r2) представляет собой долю фенотипической дисперсии, относящуюся к различиям в повторных измерениях одного и того же субъекта, возникающие из более поздних записей. Он используется, в частности, для долгоживущих видов. Это значение может быть определено только для признаков, которые проявляются несколько раз в течение жизни организма, таких как масса тела взрослого человека, скорость метаболизма или размер помета. Например, индивидуальная масса при рождении не будет иметь значения повторяемости, но будет иметь значение наследуемости. Обычно, но не всегда, повторяемость указывает на верхний уровень наследуемости.[54]
р2 = (с²грамм + s²PE) / с²п
где s²PE = взаимодействие фенотипа и окружающей среды = повторяемость.
Однако вышеупомянутая концепция повторяемости проблематична для признаков, которые обязательно сильно изменяются между измерениями. Например, масса тела у многих организмов в период от рождения до взрослого возраста значительно увеличивается. Тем не менее, в пределах данного возрастного диапазона (или стадии жизненного цикла) можно проводить повторные измерения, и на этом этапе повторяемость будет иметь значение.
Отношение
С точки зрения наследственности родственники - это люди, унаследовавшие гены от одного или нескольких общих предков. Следовательно, их "отношения" могут быть количественно на основе вероятности того, что каждый из них унаследовал копию аллеля от общего предка. В предыдущих разделах Коэффициент инбридинга была определена как «вероятность того, что два одно и тоже аллели ( А и А, или же а и а ) имеют общее происхождение »- или, более формально,« Вероятность того, что два гомологичных аллеля являются аутозиготными ». Раньше акцент делался на вероятности наличия у человека двух таких аллелей, и коэффициент был сформирован соответствующим образом. Однако это очевидно. , что эта вероятность автозиготности для особи также должна быть вероятностью того, что каждый из ее два родителя имел этот аутозиготный аллель. В этой перефокусированной форме вероятность называется коэффициент родословной для двух человек я и j ( ж ij ). В этой форме его можно использовать для количественной оценки отношений между двумя людьми, и он также может быть известен как коэффициент родства или коэффициент кровного родства.[13]:132–143 [14]:82–92
Анализ родословной
Родословные представляют собой диаграммы семейных связей между людьми и их предками и, возможно, между другими членами группы, которые разделяют с ними генетическое наследие. Это карты отношений. Таким образом, родословная может быть проанализирована, чтобы выявить коэффициенты инбридинга и совместного предка. Такие родословные на самом деле являются неформальными изображениями диаграммы пути как используется в анализ пути, который был изобретен Сьюэлом Райтом, когда он сформулировал свои исследования по инбридингу.[55]:266–298 Используя диаграмму рядом, вероятность того, что особи «B» и «C» получили аутозиготные аллели от предка «A», равна 1/2 (один из двух диплоидных аллелей). Это инбридинг "de novo" (ΔfПед) на этом этапе. Однако другой аллель мог иметь "переходящую" автозиготность от предыдущих поколений, поэтому вероятность этого составляет (de novo дополнение умноженный на инбридинг предка А ), то есть (1 - ΔfПед ) fА = (1/2) fА. Следовательно, полная вероятность аутозиготности у B и C после двойного ветвления родословной является суммой этих двух компонентов, а именно (1/2) + (1/2) жА = (1/2) (1 + ж А ) . Это можно рассматривать как вероятность того, что две случайные гаметы от предка A несут аутозиготные аллели, и в этом контексте называется коэффициент отцовства ( жAA).[13]:132–143[14]:82–92 Часто встречается в следующих абзацах.
Следуя пути «B», вероятность того, что любой аутозиготный аллель «передается» каждому последующему родителю, снова составляет (1/2) на каждом шаге (включая последний до «целевого» Икс ). Таким образом, общая вероятность перехода по «пути B» составляет (1/2)3. Степень, до которой возводится (1/2), можно рассматривать как «количество промежуточных звеньев на пути между А и Икс ", пB = 3 . Аналогично, для "пути C", пC = 2 , а «вероятность перехода» равна (1/2)2. Комбинированная вероятность аутозиготного переноса от А к Икс следовательно является [fAA (1/2)(пB) (1/2)(пC) ] . Напоминая, что жAA = (1/2) (1 + f А ) , жИкс = fPQ = (1/2)(пB + пC + 1) (1 + жА ) . В этом примере, предполагая, что fА = 0, жИкс = 0.0156 (округлено) = жPQ, одна мера "родства" между п и Q.
В этом разделе степени (1/2) использовались для представления «вероятности автозиготности». Позже этот же метод будет использован для представления пропорций наследственных генофондов, которые наследуются по родословной [раздел «Связь между родственниками»].
Правила перекрестного умножения
В следующих разделах, посвященных скрещиванию братьев и сестер, и подобным темам будет полезен ряд «правил усреднения». Они происходят из анализ пути.[55] Правила показывают, что любой коэффициент родословной может быть получен как среднее перекрестное родство между соответствующими прародительскими и родительскими комбинациями. Таким образом, ссылаясь на соседнюю диаграмму, Кросс-множитель 1 в том, что жPQ = среднее значение ( жAC , жОБЪЯВЛЕНИЕ , ждо н.э , жBD ) = (1/4) [fAC + fОБЪЯВЛЕНИЕ + fдо н.э + fBD ] = жY. Аналогичным образом кросс-множитель 2 утверждает, что жПК = (1/2) [fAC + fдо н.э ]-пока кросс-множитель 3 утверждает, что жPD = (1/2) [fОБЪЯВЛЕНИЕ + fBD ] . Возвращаясь к первому множителю, теперь видно, что он также жPQ = (1/2) [fПК + fPD ], который после подстановки множителей 2 и 3 возвращается в исходный вид.
В большинстве случаев поколение прародителей упоминается как (т-2) , родительское поколение как (т-1) , а «целевое» поколение - как т.
Фулл-сиб кросс (ФС)
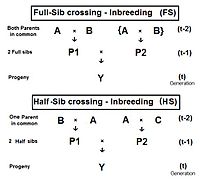
На диаграмме справа показано, что полный родственный скрещивание является прямым применением кросс-множитель 1, с небольшими изменениями, которые родители А и Б повторить (вместо C и D), чтобы указать, что люди P1 и P2 иметь оба их общие родители - то есть они полные братья и сестры. Индивидуальный Y является результатом скрещивания двух полных братьев и сестер. Следовательно, жY = fP1, P2 = (1/4) [fAA + 2 жAB + fBB ] . Напомним, что жAA и жBB были определены ранее (в анализе родословной) как коэффициенты отцовства, равно (1/2) [1 + fА ] и (1/2) [1 + fB ] соответственно, в данном контексте. Осознайте, что в этом облике бабушка и дедушка А и B представлять поколение (т-2) . Таким образом, если предположить, что в любом поколении все уровни инбридинга одинаковы, эти два коэффициенты отцовства каждый представляет (1/2) [1 + f(т-2) ] .
Теперь рассмотрим жAB. Напомним, что это тоже жP1 или же жP2, и так представляет их поколение - ж(т-1). Собирая все вместе, жт = (1/4) [2 фAA + 2 жAB ] = (1/4) [1 + f(т-2) + 2 ж(т-1) ] . Это коэффициент инбридинга за Переход Фулл-Сиб .[13]:132–143[14]:82–92 График слева показывает скорость этого инбридинга в течение двадцати повторяющихся поколений. «Повторение» означает, что потомство после цикла т стать родителями скрещивания, которые генерируют цикл (т + 1 ), и так далее. На графиках также показан инбридинг для случайное оплодотворение 2N = 20 для сравнения. Напомним, что этот коэффициент инбридинга для потомства Y также коэффициент родословной для его родителей, и это мера родство двух братьев и сестер Филл.
Полусиб скрещивание (HS)
Вывод полусиб скрещивание идет немного другим путем, чем полные братья и сестры. На соседней диаграмме у двух братьев-сестер в поколении (t-1) есть только один общий родитель - родитель «A» в поколении (t-2). В кросс-множитель 1 снова используется, давая жY = f(P1, P2) = (1/4) [fAA + fAC + fBA + fдо н.э ] . Есть только один коэффициент отцовства на этот раз, но три коэффициенты родословной на уровне (t-2) (один из них - fдо н.э- быть «манекеном» и не представлять реального человека в поколении (t-1)). Как и прежде, коэффициент отцовства является (1/2) [1 + fА ] , а три совместные предки каждый представляет ж(т-1). Напоминая, что жА представляет ж(т-2), окончательный сбор и упрощение терминов дает жY = fт = (1/8) [1 + f(т-2) + 6 ж(т-1) ] .[13]:132–143[14]:82–92 Графики слева включают это полусиб (HS) инбридинг более двадцати поколений подряд.
Как и раньше, это также позволяет количественно оценить родство двух полусибсов в поколении (t-1) в альтернативной форме ж(P1, P2).
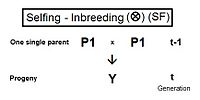
Самооплодотворение (SF)
Справа - родословная для самоопыления. Это настолько просто, что не требует каких-либо правил перекрестного умножения. Он использует только базовое сопоставление коэффициент инбридинга и его альтернатива коэффициент родословной; с последующим признанием того, что в данном случае последний также является коэффициент отцовства. Таким образом, жY = f(P1, P1) = fт = (1/2) [1 + f(т-1) ] .[13]:132–143[14]:82–92 Это самая высокая скорость инбридинга среди всех типов, как видно на графиках выше. Кривая самоопыления фактически представляет собой график коэффициент отцовства.
Кузинс переходы
Они получены с помощью методов, аналогичных методам для братьев и сестер.[13]:132–143[14]:82–92 Как и прежде, родословная точка зрения коэффициент инбридинга обеспечивает меру "родства" между родителями P1 и P2 в этих двоюродных выражениях.
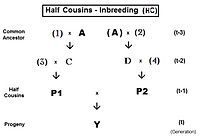
Родословная на Двоюродные братья (FC) дан вправо. Простое уравнение жY = fт = fP1, P2 = (1/4) [f1D + f12 + fCD + fC2 ]. После замены соответствующими коэффициентами инбридинга, сбора терминов и упрощения это становится жт = (1/4) [3 f(т-1) + (1/4) [2 ж(т-2) + f(т-3) + 1 ]] , который представляет собой итерационную версию, полезную для наблюдения за общей закономерностью и для компьютерного программирования. «Окончательная» версия жт = (1/16) [12 f(т-1) + 2 ж(т-2) + f(т-3) + 1 ] .
В Тройные кузены (SC) родословная слева. Родители в родословной, не имеющие отношения к общий предок обозначаются цифрами вместо букв. Здесь простое уравнение жY = fт = fP1, P2 = (1/4) [f3F + f34 + fEF + fE4 ]. После проработки соответствующей алгебры это становится жт = (1/4) [3 f(т-1) + (1/4) [3 ф(т-2) + (1/4) [2 ж(т-3) + f(т-4) + 1 ]]] , который является итерационной версией. «Финальная» версия жт = (1/64) [48 f(т-1) + 12 ж(т-2) + 2 ж(т-3) + f(т-4) + 1 ] .
Чтобы визуализировать образец в полном двоюродном брате уравнения, начните серию с полный брат уравнение переписывается в итерационной форме: жт = (1/4) [2 ф(т-1) + f(т-2) + 1 ]. Обратите внимание, что это «основной план» последнего члена в каждой из итеративных форм двоюродных братьев: с той небольшой разницей, что индексы поколения увеличиваются на «1» на каждом «уровне» двоюродного брата. Теперь определим кузен уровень в качестве k = 1 (для двоюродных братьев и сестер), = 2 (для троюродных братьев), = 3 (для троюродных братьев) и т. д .; и = 0 (для Полных Сибсов, которые являются «кузенами нулевого уровня»). В последний семестр теперь можно записать как: (1/4) [2 ф(т- (1 + к)) + f(т- (2 + к)) + 1] . Сложены перед этим последний семестр один или несколько приращения итерации в виде (1/4) [3 ф(т-д) + ... , куда j это индекс итерации и принимает значения из 1 ... k по мере необходимости в последующих итерациях. Объединение всего этого дает общую формулу для всех уровней полный двоюродный брат возможно, в том числе Полные сестры. За kth уровень полные кузены, f {k}т = Ιterj = 1k {(1/4) [3 ф(т-д) + }j + (1/4) [2 ж(т- (1 + к)) + f(т- (2 + к)) + 1] . В начале итерации все f(т-Икс) установлены на «0», и каждое значение подставляется по мере того, как оно рассчитывается по поколениям. Графики справа показывают последовательное инбридинг для нескольких уровней полных кузенов.
За двоюродные братья и сестры (FHC), слева родословная. Обратите внимание, что есть только один общий предок (индивидуальный А). Также, что касается троюродные братья, родители, не относящиеся к общему предку, обозначены цифрами. Здесь простое уравнение жY = fт = fP1, P2 = (1/4) [f3D + f34 + fCD + fC4 ]. После проработки соответствующей алгебры это становится жт = (1/4) [3 f(т-1) + (1/8) [6 ж(т-2) + f(т-3) + 1 ]] , который является итерационной версией. «Окончательная» версия жт = (1/32) [24 f(т-1) + 6 ж(т-2) + f(т-3) + 1 ] . Алгоритм итерации аналогичен таковому для полные кузены, за исключением того, что последний член (1/8) [6 ж(т- (1 + к)) + f(т- (2 + к)) + 1 ] . Обратите внимание, что этот последний член в основном похож на уравнение половинных братьев, параллельно с образцом для полных кузенов и полных братьев и сестер. Другими словами, полукровные братья - это полукузины «нулевого уровня».
Существует тенденция рассматривать скрещивание кузенов с ориентированной на человека точки зрения, возможно, из-за широкого интереса к генеалогии. Использование родословных для получения инбридинга, возможно, укрепляет эту точку зрения «семейной истории». Однако такие виды скрещивания встречаются и в естественных популяциях, особенно в тех, которые ведут оседлый образ жизни или имеют «нерестилища», которые они повторно посещают из сезона в сезон. Группа потомства гарема с доминантным самцом, например, может содержать элементы однояйцевого, двоюродного и обратного скрещивания, а также генетического дрейфа, особенно «островного» типа. Вдобавок к этому случайное «ауткроссирование» добавляет в смесь элемент гибридизации. это нет панмиксия.
Бэккроссинг (BC)
После гибридизации между А и р, то F1 (индивидуальный B) перекрещивается (BC1) исходному родителю (р) для производства BC1 поколение (индивидуальный C). [Обычно для акта изготовление обратный крест и для произведенного им поколения. Акт обратного пересечения здесь, в курсив. ] Родитель р это повторяющийся родитель. Изображены два последовательных обратных креста с индивидуальным D будучи BC2 поколение. Этим поколениям было дано т индексы также, как указано. Как прежде, жD = fт = fCR = (1/2) [fРБ + fRR ] , с помощью кросс-множитель 2 ранее дано. В жРБ только что определено - это тот, который включает в себя поколение (т-1) с (т-2). Однако есть еще один такой жРБ содержится полностью в поколение (т-2) также, и это это тот, который используется сейчас: как родословная из родители отдельных C в поколении (т-1). Таким образом, это также коэффициент инбридинга из C, а значит, ж(т-1). Остальные жRR это коэффициент отцовства из повторяющийся родитель, и так (1/2) [1 + fр ] . Собираем все вместе: жт = (1/2) [(1/2) [1 + fр ] + f(т-1) ] = (1/4) [1 + fр + 2 ж(т-1) ] . Графики справа иллюстрируют инбридинг обратного скрещивания более чем двадцати обратных скрещиваний для трех различных уровней (фиксированного) инбридинга у рекуррентного родителя.
Эта процедура обычно используется в программах селекции животных и растений. Часто после создания гибрида (особенно если особи недолговечны) рекурсивному родителю требуется отдельное «линейное разведение» для его сохранения в качестве будущего рецидивирующего родителя при обратном скрещивании. Это поддержание может происходить посредством самоопыления или скрещивания полукровных или полусибских племен, или через ограниченные случайно оплодотворенные популяции, в зависимости от репродуктивных возможностей вида. Конечно, этот постепенный рост жр переносится в жт обратного скрещивания. Результатом является более постепенный подъем кривой к асимптотам, чем показано на настоящих графиках, потому что жр не находится на фиксированном уровне с самого начала.
Вклады наследственных генофондов
В разделе «Анализ родословной», использовался для представления вероятностей наследования аутозиготного аллеля более п поколений вниз по ветвям родословной. Эта формула возникла из-за правил, налагаемых половым размножением: (я) два родителя, вносящие практически равные доли аутосомных генов, и (ii) последовательное разбавление для каждого поколения между зиготой и «фокусным» уровнем отцовства. Эти же правила применимы и к любой другой точке зрения происхождения в двуполой репродуктивной системе. Одним из них является доля любого наследственного генофонда (также известного как «зародышевая плазма»), который содержится в генотипе любой зиготы.
Следовательно, доля наследственный генофонд в генотипе есть:
Например, каждый родитель определяет генофонд, способствующий своему потомству; в то время как каждый прадедушка вносит свой вклад своему праправнуку.
Общий генофонд зиготы (Γ) - это, конечно, сумма сексуальных вкладов в его происхождение.
Отношения через наследственные генофонды
Очевидно, что люди, произошедшие от общего генофонда предков, связаны между собой. Это не означает, что они идентичны по своим генам (аллелям), потому что на каждом уровне предка будет происходить сегрегация и ассортимент при производстве гамет. Но они будут происходить из того же пула аллелей, доступного для этих мейозов и последующих оплодотворений. [Эта идея впервые возникла в разделах, посвященных анализу родословных и родственным связям.] Вклад генофонда [см. Раздел выше] их ближайший общий наследственный генофонд(ан наследственный узел), следовательно, можно использовать для определения их отношений. Это приводит к интуитивному определению отношений, которое хорошо согласуется со знакомыми понятиями «родства», обнаруженными в семейной истории; и позволяет сравнивать «степень родства» сложных моделей отношений, проистекающих из такой генеалогии.
Единственные необходимые модификации (по очереди для каждого индивидуума) находятся в Γ и связаны с переходом к «общему общий родословная ", а не" индивидуум " общий происхождение ". Для этого определите Ρ (вместо Γ) ; m = количество общих предков в узле (т.е. только m = 1 или 2); и «индивидуальный индекс» k. Таким образом:
где, как и раньше, n = количество половых поколений между индивидуумом и наследственным узлом.
Примером могут служить два двоюродных брата.Их ближайший общий наследственный узел - это их бабушка и дедушка, которые дали начало их родным братьям и сестрам, и у них обоих общих дедушек и бабушек. [См. Более раннюю родословную.] В этом случае м = 2 и п = 2, поэтому для каждого из них
В этом простом случае каждый двоюродный брат имеет одинаковое число Ρ.
Второй пример может быть между двумя двоюродными братьями, но один (k = 1) имеет три поколения назад до предкового узла (n = 3), а другое (k = 2) только два (n = 2) [т.е. троюродные и двоюродные отношения]. Для обоих m = 2 (они полные кузены).
и
Обратите внимание, у каждого кузена свой Ρ k.
GRC - коэффициент родства генофонда
В любой оценке парных отношений есть одно Ρk для каждого индивидуума: осталось их усреднить, чтобы объединить в единый «Коэффициент родства». Потому что каждый Ρ это доля от общего генофонда, подходящим средним для них является среднее геометрическое [56][57]:34–55 Это среднее значение их Коэффициент родства генного пула- «ГРК».
Для первого примера (два полных двоюродных брата) их GRC = 0,5; для второго случая (полные двоюродные братья и сестры) их GRC = 0,3536.
Все эти отношения (GRC) являются приложениями анализа пути.[55]:214–298 Ниже приводится краткое изложение некоторых уровней взаимоотношений (GRC).
| GRC | Примеры отношений |
|---|---|
| 1.00 | полные сибсы |
| 0.7071 | Родитель ↔ Потомство; Дядя / Тетя ↔ Племянник / Племянница |
| 0.5 | полные двоюродные братья и сестры; полусибсы; grand Parent ↔ grand Offspring |
| 0.3536 | полные кузены Первый ↔ Второй; полные двоюродные братья {1 remove} |
| 0.25 | полные троюродные братья; половина двоюродных братьев и сестер; полные двоюродные братья {2 удаляет} |
| 0.1768 | полный двоюродный брат {3 удаляет}; полные троюродные братья {1 remove} |
| 0.125 | полные троюродные братья; половина троюродных братьев; полные двоюродные братья {4 удаляет} |
| 0.0884 | полные двоюродные братья {5 удаляет}; половина троюродных братьев {1 remove} |
| 0.0625 | полные четвертые кузены; наполовину третьи кузены |
Сходства между родственниками
Они, как и генотипические отклонения, могут быть получены либо с помощью метода генной модели («Матер»), либо с помощью подхода замещения аллеля («Фишер»). Здесь каждый метод демонстрируется для альтернативных случаев.
Ковариация родителей и потомков
Их можно рассматривать либо как ковариацию между любым потомком и кто угодно своих родителей (PO), или как ковариацию между любым потомком и "средний родитель" ценность обоих родителей (MPO).
Неполный родитель и потомство (ПО)
Это можно вывести как сумма перекрестных продуктов между родительскими генными эффектами и одна половина ожиданий потомства с использованием метода замены аллеля. В одна половина ожидания потомства объясняет тот факт, что только один из двух родителей рассматривается. Следовательно, соответствующие родительские генные эффекты представляют собой переопределенные генные эффекты второй стадии, использованные для определения генотипических отклонений ранее, а именно: а ″ = 2q (а - qd) и d ″ = (q-p) a + 2pqd а также (-a) ″ = -2p (a + pd) [см. раздел «Новое определение генных эффектов»]. Точно так же соответствующие эффекты потомства, для ожидания замены аллеля наполовину меньше племенные ценности, последний из которых: аAA = 2qa, и аАа = (д-р) а а также ааа = -2 Па [см. раздел «Замена генотипа - ожидания и отклонения»].
Поскольку все эти эффекты уже определены как отклонения от среднего генотипа, сумма перекрестного произведения с использованием {частота генотипа * эффект родительского гена * полубнительная ценность} немедленно предоставляет ковариация ожидания замещения аллеля между одним из родителей и его потомством. После тщательного сбора терминов и упрощений это становится cov (PO)А = pqa2 = ½ с2А.[13] :132–141[14] :134–147
К сожалению, отклонения замещения аллелей обычно упускаются из виду, но тем не менее они не «перестали существовать»! Напомним, что это отклонения: dAA = -2q2 d, и dАа = 2pq d а также dаа = -2p2 d [см. раздел «Замена генотипа - ожидания и отклонения»]. Следовательно, сумма перекрестного произведения с использованием {частота генотипа * эффект родительского гена * отклонения половинной замены} также сразу же обеспечивает ковариацию отклонений замещения аллелей между одним из родителей и его потомками. Еще раз, после тщательного сбора терминов и упрощений, это становится cov (PO)D = 2p2q2d2 = ½ с2D.
Отсюда следует, что: cov (PO) = cov (PO)А + cov (PO)D = ½ с2А + ½ с2D, когда доминирование нет упускается из виду!
Средний родитель и потомство (MPO)
Поскольку существует множество комбинаций родительских генотипов, существует множество различных способов получения промежуточных родителей и потомков, а также различные частоты получения каждой родительской пары. В этом случае наиболее целесообразен генно-модельный подход. Следовательно, нескорректированная сумма перекрестных продуктов (USCP)—Использование всех продуктов { частота родительской пары * эффект среднего родительского гена * среднее значение генотипа потомства } - корректируется вычитанием {общее среднее значение генотипа}2 в качестве поправочный коэффициент (CF). После умножения всех различных комбинаций, тщательного сбора терминов, упрощения, факторинга и отмены, где это применимо, это становится:
cov (MPO) = pq [a + (q-p) d]2 = pq a2 = ½ с2А, причем в данном случае не было упущено из виду доминирование, поскольку оно использовалось при определении а.[13] :132–141[14] :134–147
Приложения (родитель-потомок)
Наиболее очевидным применением является эксперимент, в котором участвуют все родители и их потомки, с реципрокными скрещиваниями или без них, предпочтительно реплицируемые без предвзятости, что позволяет оценить все подходящие средние значения, дисперсии и ковариации вместе с их стандартными ошибками. Эти оценочные статистические данные затем можно использовать для оценки генетических отклонений. Дважды разница между оценками двух форм (скорректированной) ковариации родителей и потомков дает оценку s2D; и вдвое больше cov (MPO) оценки s2А. При соответствующем экспериментальном дизайне и анализе,[9][49][50] Стандартные ошибки также могут быть получены для этой генетической статистики. Это основная суть эксперимента, известного как Диаллельный анализ, версия которого Мэзера, Джинкса и Хеймана обсуждается в другом разделе.
Второе приложение предполагает использование регрессивный анализ, который оценивает на основе статистики ординату (Y-оценка), производную (коэффициент регрессии) и константу (Y-пересечение) исчисления.[9][49][58][59] В коэффициент регрессии оценивает скорость изменения функции прогнозирования Y из Икс, основанный на минимизации остатков между подобранной кривой и наблюдаемыми данными (MINRES). Никакой альтернативный метод оценки такой функции не удовлетворяет этому основному требованию MINRES. В целом коэффициент регрессии оценивается как отношение ковариации (XY) к дисперсии определителя (X). На практике размер выборки обычно одинаков как для X, так и для Y, поэтому его можно записать как SCP (XY) / SS (X), где все термины были определены ранее.[9][58][59] В данном контексте родители рассматриваются как «определяющая переменная» (X), а потомство как «определяемая переменная» (Y), а коэффициент регрессии - как «функциональная взаимосвязь» (ßPO) между двумя. Принимая cov (MPO) = ½ с2А в качестве cov (XY), и s2п / 2 (дисперсия среднего значения двух родителей - среднего родителя) как s2Икс, видно, что SSMPO = [½ с2А] / [½ с2п] = h2.[60] Далее, используя cov (PO) = [½ с2А + ½ с2D ] в качестве cov (XY), и s2п в качестве s2Икс, видно, что 2 ßPO = [2 (½ с2А + ½ с2D )] / с2п = H2.
Анализ эпистаз ранее предпринималась попытка дисперсия взаимодействия подход типа s2AA, и s2ОБЪЯВЛЕНИЕ а также s2DD. Это было объединено с этими существующими ковариациями, чтобы предоставить оценки дисперсий эпистаза. Однако результаты эпигенетики предполагают, что это не может быть подходящим способом определения эпистаза.
Ковариации братьев и сестер
Ковариация между сводными братьями и сестрами (HS) легко определяется с помощью методов замены аллелей; но, опять же, исторически не учитывалась роль доминирования. Однако, как и в случае ковариации среднего родителя / потомка, ковариация между полноправными братьями и сестрами (FS) требует подхода «родительской комбинации», что требует использования метода скорректированных перекрестных продуктов генной модели; и влияние доминирования исторически не игнорировалось. Превосходство производных генной модели здесь так же очевидно, как и для генотипических вариаций.
Сводные братья и сестры одного общего родителя (HS)
Сумма перекрестных произведений {частота общего родителя * полубесплодная ценность одного полусиба * полувековая ценность любого другого полусиба в той же группе общих родителей} немедленно обеспечивает одну из требуемых ковариаций, поскольку использованные эффекты [племенные ценности- представляющие ожидания замены аллеля] уже определены как отклонения от среднего генотипа [см. Раздел «Замена аллеля - ожидания и отклонения»]. После упрощения. это становится: cov (HS)А = ½ pq a2 = ¼ s2А.[13] :132–141[14] :134–147 Тем не менее отклонения замещения также существуют, определяя сумму перекрестных продуктов {частота общего родителя * половинное отклонение замещения одного полусиба * половинное отклонение замещения любого другого полусиба в той же общей родительской группе}, что в конечном итоге приводит к: cov (HS)D = p2 q2 d2 = ¼ s2D. Добавление двух компонентов дает:
cov (HS) = cov (HS)А + cov (HS)D = ¼ s2А + ¼ с2D.
Полные братья (FS)
Как объяснялось во введении, используется метод, аналогичный тому, который используется для ковариации среднего родителя / потомка. Следовательно, нескорректированная сумма перекрестных продуктов (USCP) с использованием всех продуктов - { частота родительской пары * квадрат среднего значения генотипа потомства } - корректируется вычитанием {общее среднее значение генотипа}2 в качестве поправочный коэффициент (CF). В этом случае перемножение всех комбинаций, тщательный сбор терминов, упрощение, разложение на множители и исключение очень затягиваются. В конечном итоге это становится:
cov (FS) = pq a2 + p2 q2 d2 = ½ с2А + ¼ с2D, при этом не было упущено ни одно доминирование.[13] :132–141[14] :134–147
Приложения (братья и сестры)
Самым полезным приложением для генетической статистики здесь является корреляция между сводными братьями и сестрами. Напомним, что коэффициент корреляции (р) - это отношение ковариации к дисперсии [например, см. раздел «Связанные атрибуты»]. Следовательно, рHS = cov (HS) / с2все HS вместе = [¼ s2А + ¼ с2D ] / с2п = ¼ H2.[61] Корреляция между полноправными братьями и сестрами бесполезна, поскольку рFS = cov (FS) / с2все ФС вместе = [½ с2А + ¼ с2D ] / с2п. Предположение, что он "приближается" (½ часа2) плохой совет.
Конечно, корреляции между братьями и сестрами представляют интерес сами по себе, совершенно независимо от того, какую пользу они могут иметь для оценки наследственности или генотипических отклонений.
Возможно, стоит отметить, что [cov (FS) - cov (HS)] = ¼ s2А. Эксперименты, состоящие из семейств FS и HS, могли бы использовать это, используя внутриклассовую корреляцию, чтобы приравнять экспериментальные компоненты дисперсии к этим ковариациям [см. Раздел «Коэффициент взаимосвязи как внутриклассовая корреляция» для обоснования этого).
Предыдущие комментарии относительно эпистаза снова применимы здесь [см. Раздел «Приложения (Родители-потомки»]).
Выбор
Основные принципы
Отбор работает с атрибутом (фенотипом), так что особи, которые равны или превышают порог отбора (гп) стать эффективными родителями для следующего поколения. В пропорция они представляют базовую популяцию давление отбора. В меньше пропорция, сильнее давление. В среднее значение выбранной группы (Пs) превосходит среднее базовое население (П0) по разнице, называемой дифференциал выбора (S). Все эти количества фенотипичны. Чтобы «связать» с лежащими в основе генами, наследственность (час2) используется, выполняя роль коэффициент детерминации в биометрическом смысле. В ожидаемое генетическое изменение- все еще выражается в фенотипические единицы измерения- называется генетический прогресс (ΔG), и получается как произведение дифференциал выбора (S) и это коэффициент детерминации (час2). Ожидаемый среднее потомство (П1) находится путем добавления генетический прогресс (ΔG) к базовое среднее (P0). Графики справа показывают, насколько (начальный) генетический прогресс больше при более сильном давлении отбора (меньше вероятность). Они также показывают, как прогресс от последовательных циклов отбора (даже при одном и том же давлении отбора) неуклонно снижается, потому что фенотипическая дисперсия и наследственность уменьшаются самим отбором. Это обсуждается ниже.
Таким образом .[14] :1710–181и .[14] :1710–181
В узко-смысловая наследственность (h2) обычно используется, тем самым ссылаясь на генная дисперсия (σ2А) . Однако при необходимости использование наследуемость в широком смысле (H2) подключится к генотипическая дисперсия (σ2грамм) ; и даже возможно аллельная наследуемость [h2Европа = (σ2а) / (σ2п) ] можно было бы рассмотреть, подключившись к (σ2а ). [См. Раздел о наследственности.]
Чтобы применить эти концепции перед выбор действительно имеет место, и поэтому можно предсказать результат альтернатив (например, выбор порог выбора, например), эти фенотипические статистические данные пересматриваются с учетом свойств нормального распределения, особенно тех, которые касаются усечения верхний хвост Распределения. При таком рассмотрении стандартизированный дифференциал выбора (i) ″ и стандартизированный порог отбора (z) ″ используется вместо предыдущих «фенотипических» версий. В фенотипическое стандартное отклонение (σП (0)) тоже нужен. Это описано в следующем разделе.
Следовательно, ΔG = (i σп) ч2, куда (я σП (0)) = S ранее.[14] :1710–181
В тексте выше отмечалось, что последовательные ΔG снижается, потому что "вход" [ фенотипическая дисперсия (σ2п )] уменьшается предыдущим выбором.[14]:1710–181 Наследственность также снижена. Графики слева показывают это снижение за десять циклов повторного выбора, в течение которых подтверждается то же давление выбора. Накопленный генетический прогресс (ΣΔG) практически достигла своей асимптоты к поколению 6 в этом примере. Это сокращение частично зависит от свойств усечения нормального распределения и частично от наследуемости вместе с определение мейоза (б2 ). Последние два пункта определяют степень, в которой усечение "компенсируется" новыми вариациями, возникающими в результате сегрегации и ассортимента во время мейоза.[14] :1710–181[27] Это скоро будет обсуждаться, но здесь обратите внимание на упрощенный результат для недисперсное случайное оплодотворение (f = 0).
Таким образом : σ2П (1) = σ2П (0) [1 - i (i-z) ½ ч.2], куда i (i-z) = K = коэффициент усечения и ½ часа2 = R = коэффициент воспроизводства[14]:1710–181[27] Это можно также записать как σ2П (1) = σ2П (0) [1 - K R], что облегчает более подробный анализ проблем выбора.
Здесь, я и z уже определены, ½ это определение мейоза (б2) за f = 0, а оставшийся символ - наследственность. Они обсуждаются далее в следующих разделах. Также обратите внимание, что в целом R = b2 час2. Если генерал определение мейоза (б2 ) , результаты предыдущего инбридинга могут быть включены в отбор. Уравнение фенотипической дисперсии становится таким:
σ2П (1) = σ2П (0) [1 - i (i-z) b2 час2].
В Фенотипическая дисперсия усечен выбранная группа ( σ2P (S) ) просто σ2П (0) [1 - K], и в нем генная дисперсия является (час20 σ2P (S) ). Предполагая, что выбор не изменил относящийся к окружающей среде дисперсия, генная дисперсия для потомства может быть приблизительно σ2А (1) = (σ2П (1) - σ2E) . Из этого, час21 = (σ2А (1) / σ2П (1) ). Аналогичные оценки можно сделать для σ2G (1) и ЧАС21 , или для σ2а (1) и час2ЕС (1) если необходимо.
Альтернатива ΔG
Следующая перестановка полезна для рассмотрения выбора по нескольким атрибутам (символам). Он начинается с расширения наследуемости до ее компонентов дисперсии. ΔG = i σп (σ2А / σ2п ) . В σп и σ2п частично отменить, оставив соло σп. Далее σ2А внутри наследственность может быть расширена как (σА × σА), что приводит к :
ΔG = i σА (σА / σп ) = я σА час .
Соответствующие изменения могут быть выполнены с использованием альтернативной наследственности, давая ΔG = i σграмм ЧАС или же ΔG = i σа часЕвропа.
Полигенные модели адаптации в популяционной генетике
Этот традиционный взгляд на адаптацию в количественной генетике обеспечивает модель того, как выбранный фенотип изменяется с течением времени в зависимости от дифференциала отбора и наследуемости. Однако он не дает понимания (и не зависит от) каких-либо генетических деталей - в частности, количества задействованных локусов, их частоты аллелей и величины эффекта, а также частотных изменений, вызванных отбором. На этом, напротив, сосредоточена работа над полигенная адаптация[62] в области популяционная генетика. Недавние исследования показали, что такие черты, как рост, развились у людей за последние несколько тысяч лет в результате небольших сдвигов частоты аллелей в тысячах вариантов, которые влияют на рост.[63][64][65]
Фон
Стандартизированный отбор - нормальное распределение
Целиком базовое население очерчивается нормальной кривой[59]:78–89 Направо. Вдоль Ось Z - это каждое значение атрибута от наименьшего к наибольшему, а высота от этой оси до самой кривой - это частота значения на оси ниже. Уравнение для нахождения этих частот для «нормальной» кривой (кривая «обычного опыта») дано в виде эллипса. Обратите внимание, что он включает в себя среднее значение (µ) и дисперсия (σ2). Двигаясь бесконечно малым образом по оси z, частоты соседних значений можно «сложить» рядом с предыдущими, тем самым накапливая область, представляющую вероятность получения всех значений в стеке. [Это интеграция из исчисления.] Выбор фокусируется на такой вероятностной области, являющейся затененной областью из порог выбора (z) до конца верхнего хвоста кривой. Это давление отбора. Выбранная группа (эффективные родители следующего поколения) включает все значения фенотипа из z до «конца» хвоста.[66] Среднее значение выбранная группа является µs, а разница между ним и базовым средним (µ) представляет собой дифференциал выбора (S). Путем частичного интегрирования по интересующим участкам кривой и некоторой перестройки алгебры можно показать, что «дифференциал выбора» равен S = [y (σ / Вероятность)] , куда у это частота значения на «пороге выбора» z (в ордината из z).[13]:226–230 Изменение этих отношений дает S / σ = y / Вероятность., левая часть которого, по сути, дифференциал выбора, деленный на стандартное отклонение-это стандартизированный дифференциал выбора (i). Правая часть отношения обеспечивает «оценку» для я- ордината порог выбора разделенный на давление отбора. Таблицы нормального распределения[49] :547–548 можно использовать, но таблицы я сам имеется также.[67]:123–124 Последняя ссылка также дает значения я с поправкой на небольшую популяцию (400 и меньше),[67]:111–122 где нельзя предполагать "квазибесконечность" (но был предполагается в схеме «Нормальное распределение» выше). В стандартизированный дифференциал выбора (я) известен также как интенсивность отбора.[14]:174 ; 186
Наконец, может быть полезна перекрестная ссылка с другой терминологией из предыдущего подраздела: µ (здесь) = "P0" (там), µS = "PS" и σ2 = "σ2п".
Определение мейоза - анализ репродуктивного пути
В определение мейоза (б2) это коэффициент детерминации мейоза, то есть деления клеток, при котором родители производят гаметы. Следуя принципам стандартизированная частичная регрессия, из которых анализ пути является графически ориентированной версией, Сьюэлл Райт проанализировал пути потока генов во время полового размножения и установил «сильные стороны вклада» (коэффициенты детерминации) различных компонентов к общему результату.[27][37] Анализ пути включает частичные корреляции а также коэффициенты частичной регрессии (последние являются коэффициенты пути). Линии с одной стрелкой являются направленными определяющие пути, а линии с двойными стрелками - это корреляционные связи. Отслеживание различных маршрутов по правила анализа пути имитирует алгебру стандартизированной частичной регрессии.[55]
Схема путей слева представляет собой анализ полового размножения. Из его интересных элементов важным в контексте выбора является мейоз. Вот где происходят сегрегация и ассортимент - процессы, которые частично улучшают усечение фенотипической дисперсии, возникающей в результате отбора. Коэффициенты пути б пути мейоза. Те, что помечены а пути оплодотворения. Соотношение гамет от одного родителя (грамм) это мейотическая корреляция. Между родителями в одном поколении рА. Что между гаметами от разных родителей (ж) впоследствии стал известен как коэффициент инбридинга.[13]:64 Штрих (') обозначает поколение (т-1), а ООНштрих указывает поколение т. Здесь приведены некоторые важные результаты настоящего анализа. Сьюэлл Райт интерпретировал многие с точки зрения коэффициентов инбридинга.[27][37]
Определение мейоза (б2) является ½ (1 + г) и равно ½ (1 + f(т-1)) , подразумевая, что g = f(т-1).[68] При недисперсном случайном внесении удобрений f(т-1)) = 0, что дает б2 = ½, как использовалось в разделе выбора выше. Однако, зная его предысторию, при необходимости можно использовать другие схемы удобрения. Другое определение также включает инбридинг - определение оплодотворения (а2) равно 1 / [2 (1 + fт ) ] . Еще одна корреляция - это показатель инбридинга -рА = 2 жт / (1 + f(т-1) ), также известный как коэффициент родства. [Не путайте это с коэффициент родства- альтернативное название для коэффициент родословной. См. Введение в раздел «Взаимоотношения».] Это рА повторяется в подразделе, посвященном дисперсии и отбору.
Эти связи с инбридингом раскрывают интересные аспекты полового размножения, которые не сразу бросаются в глаза. Графики справа показывают мейоз и сингамия (оплодотворение) коэффициенты детерминации против коэффициента инбридинга. Выявлено, что по мере увеличения инбридинга мейоз становится более важным (увеличивается коэффициент), а сингамии становится менее значимой. Общая роль воспроизводства [произведение двух предыдущих коэффициентов -р2] остается такой же.[69] Этот увеличить в б2 особенно актуален для отбора, поскольку означает, что выборочное усечение фенотипической дисперсии в меньшей степени компенсируется во время последовательности отбора, когда сопровождается инбридингом (что часто имеет место).
Генетический дрейф и отбор
В предыдущих разделах рассматривались разброс в качестве «помощника» отбор, и стало очевидно, что эти двое хорошо работают вместе. В количественной генетике отбор обычно исследуется таким «биометрическим» способом, но изменения средних значений (которые отслеживаются с помощью ΔG) отражают изменения частот аллелей и генотипов под этой поверхностью. Обращение к разделу «Генетический дрейф» напоминает о том, что он также влияет на изменения в частотах аллелей и генотипов и связанных с ними средствах; и что это сопутствующий аспект рассмотренной здесь дисперсии («другая сторона той же медали»). Однако эти две силы изменения частоты редко действуют согласованно и часто могут действовать противоположно друг другу. Один (отбор) является «направленным», управляемым давлением отбора, действующим на фенотип; другой (генетический дрейф) обусловлен «случайностью» оплодотворения (биномиальные вероятности образцов гамет). Если эти два аллеля имеют тенденцию к одной и той же частоте аллелей, их «совпадение» - это вероятность получения этой выборки частот в результате генетического дрейфа: вероятность их «конфликта», однако, равна сумма вероятностей всех альтернативных частотных выборок. В крайних случаях однократная выборка сингамии может свести на нет то, что было достигнуто, и вероятности того, что это произойдет, доступны. Об этом важно помнить. Однако генетический дрейф, приводящий к частотам выборки, аналогичным частотам выборки, не приводит к столь радикальному результату - вместо этого замедляет прогресс в достижении целей отбора.
При совместном наблюдении двух (или более) атрибутов (например рост и масса), можно заметить, что они изменяются вместе при изменении генов или окружающей среды. Эта совместная вариация измеряется ковариация, который может быть представлен как " cov "или θ.[43] Будет положительно, если они будут вместе изменяться в одном направлении; или отрицательный, если они различаются вместе, но в противоположном направлении. Если два атрибута изменяются независимо друг от друга, ковариация будет равна нулю. Степень связи между атрибутами количественно оценивается коэффициент корреляции (символ р или же ρ ). В общем, коэффициент корреляции - это отношение ковариация к среднему геометрическому [70] двух вариантов атрибутов.[59] :196–198 Наблюдения обычно происходят на фенотипе, но в исследованиях они могут также происходить на «эффективном гаплотипе» (эффективном генном продукте) [см. Рисунок справа]. Следовательно, ковариация и корреляция могут быть «фенотипическими», «молекулярными» или любым другим обозначением, которое допускает модель анализа. Фенотипическая ковариация является «самым внешним» слоем и соответствует «обычной» ковариации в биометрии / статистике. Однако его можно разделить с помощью любой подходящей исследовательской модели таким же образом, как и фенотипическая дисперсия. Для каждого разбиения ковариации существует соответствующее разбиение корреляции. Некоторые из этих разделов приведены ниже. Первый индекс (G, A и т. Д.) Указывает раздел. Индексы второго уровня (X, Y) являются «хранителями места» для любых двух атрибутов.
Первый пример - это неразделенный фенотип.
Генетические перегородки (а) «генотипический» (общий генотип),(б) "генный" (ожидания замены) и (c) "аллельный" (гомозиготный) следуют.
(а)
(б)
(c)
При правильно спланированном эксперименте негенетический Также можно получить раздел (среда).
Основные причины корреляции
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Июль 2016) |
Метаболические пути от гена к фенотипу сложны и разнообразны, но причины корреляции между атрибутами лежат внутри них. Контур показан на рисунке справа.
Смотрите также
- Искусственный отбор
- Диаллель крест
- Дуглас Скотт Фалконер
- Формула выборки Ювенса
- Экспериментальная эволюция
- Генетическая архитектура
- Генетическая дистанция
- Наследственность
- Рональд Фишер
Сноски и ссылки
- ^ Андерберг, Майкл Р. (1973). Кластерный анализ приложений. Нью-Йорк: Academic Press.
- ^ Мендель, Грегор (1866). "Versuche über Pflanzen Hybriden". Verhandlungen Naturforschender Verein в Брюнне. iv.
- ^ а б c Мендель, Грегор; Бейтсон, Уильям [переводчик] (1891 г.). «Эксперименты по гибридизации растений». Дж. Рой. Hort. Soc. (Лондон). xxv: 54–78.
- ^ The Mendel G .; Статья Бейтсона В. (1891) с дополнительными комментариями Бейтсона перепечатана в: Sinnott E.W .; Dunn L.C .; Добжанский Т. (1958). «Принципы генетики»; Нью-Йорк, Макгроу-Хилл: 419-443. Сноска 3 на странице 422 идентифицирует Бейтсона как оригинального переводчика и дает ссылку на этот перевод.
- ^ А QTL представляет собой область в геноме ДНК, которая влияет на количественные фенотипические признаки или связана с ними.
- ^ Уотсон, Джеймс Д .; Гилман, Майкл; Витковский, Ян; Золлер, Марк (1998). Рекомбинантная ДНК (Второе (7-е изд.) Изд.). Нью-Йорк: W.H. Фримен (Scientific American Books). ISBN 978-0-7167-1994-6.
- ^ Джайн, Х. К. [редактор]; Харквал, М. К. [редактор] (2004). Селекция растений - от менделевского до молекулярного подходов. Бостон Дордехт Лондон: Kluwer Academic Publishers. ISBN 978-1-4020-1981-4.CS1 maint: дополнительный текст: список авторов (связь)
- ^ а б c d Фишер, Р. А. (1918). «Корреляция между родственниками на основании менделевского наследования». Сделки Королевского общества Эдинбурга. 52 (2): 399–433. Дои:10,1017 / с0080456800012163.
- ^ а б c d е ж грамм Steel, R.G.D .; Торри, Дж. Х. (1980). Принципы и процедуры статистики (2-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 0-07-060926-8.
- ^ Иногда используются и другие символы, но они обычны.
- ^ Эффект аллеля представляет собой среднее фенотипическое отклонение гомозиготы от средней точки двух противоположных гомозиготных фенотипов в одном локусе, когда наблюдается на бесконечности всех фоновых генотипов и сред. На практике параметр заменяется оценками из больших несмещенных выборок.
- ^ Эффект доминирования представляет собой среднее фенотипическое отклонение гетерозиготы от средней точки двух гомозигот в одном локусе, когда наблюдается на бесконечности всех фоновых генотипов и сред. На практике параметр заменяется оценками из больших несмещенных выборок.
- ^ а б c d е ж грамм час я j k л м п о п q р s т ты v ш Икс у z аа ab ac объявление ае аф аг ах Crow, J. F .; Кимура, М. (1970). Введение в теорию популяционной генетики. Нью-Йорк: Харпер и Роу.
- ^ а б c d е ж грамм час я j k л м п о п q р s т ты v ш Икс у z аа ab ac объявление ае аф аг ах ай эй ак аль Falconer, D. S .; Маккей, Труди Ф. С. (1996). Введение в количественную генетику (Четвертое изд.). Харлоу: Лонгман. ISBN 978-0582-24302-6. Сложить резюме – Генетика (журнал) (24 августа 2014 г.).
- ^ Мендель прокомментировал эту особую тенденцию для F1> P1, то есть свидетельство силы гибрида по длине стебля. Однако разница может быть незначительной. (Связь между диапазоном и стандартным отклонением известна [Steel and Torrie (1980): 576], что позволяет провести приблизительный тест на значимость этой текущей разницы.)
- ^ Ричардс, А. Дж. (1986). Системы селекции растений. Бостон: Джордж Аллен и Анвин. ISBN 0-04-581020-6.
- ^ Институт Джейн Гудолл. «Социальная структура шимпанзе». Шимпанзе Централ. Архивировано из оригинал 3 июля 2008 г.. Получено 20 августа 2014.
- ^ Гордон, Ян Л. (2000). «Количественная генетика аллогамного F2: происхождение случайно оплодотворенных популяций». Наследственность. 85: 43–52. Дои:10.1046 / j.1365-2540.2000.00716.x. PMID 10971690.
- ^ F2, полученный самоопыляющиеся особи F1 (ан автогамный F2), однако, не является источником случайно оплодотворенной структуры популяции. См. Gordon (2001).
- ^ Замок, В. Э. (1903). «Закон наследственности Гальтона и Менделя и некоторые законы, регулирующие улучшение расы путем отбора». Труды Американской академии искусств и наук. 39 (8): 233–242. Дои:10.2307/20021870. HDL:2027 / hvd.32044106445109. JSTOR 20021870.
- ^ Харди, Г. Х. (1908). «Менделирующие пропорции в смешанном населении». Наука. 28 (706): 49–50. Bibcode:1908 г., наука .... 28 ... 49H. Дои:10.1126 / science.28.706.49. ЧВК 2582692. PMID 17779291.
- ^ Вайнберг, В. (1908). "Über den Nachweis der Verebung beim Menschen". Джахреш. Верейн Ф. Фатерл. Naturk, Württem. 64: 368–382.
- ^ Обычно в научной этике открытие носит имя человека, который первым его сделал. Замок, однако, похоже, был упущен из виду: позже, когда он был найден заново, название «Харди Вайнберг» стало настолько повсеместным, что казалось, что уже слишком поздно его обновлять. Может быть, равновесие «Замок Харди Вайнберг» было бы хорошим компромиссом?
- ^ а б Гордон, Ян Л. (1999). «Количественная генетика внутривидовых гибридов». Наследственность. 83 (6): 757–764. Дои:10.1046 / j.1365-2540.1999.00634.x. PMID 10651921.
- ^ Гордон, Ян Л. (2001). «Количественная генетика автогамного F2». Наследие. 134 (3): 255–262. Дои:10.1111 / j.1601-5223.2001.00255.x. PMID 11833289.
- ^ Райт, С. (1917). «Среднее соотношение внутри подгрупп населения». J. Wash. Acad. Наука. 7: 532–535.
- ^ а б c d е ж грамм Райт, С. (1921). «Системы спаривания. I. Биометрические отношения между родителем и потомством». Генетика. 6 (2): 111–123. ЧВК 1200501. PMID 17245958.
- ^ Sinnott, Edmund W .; Dunn, L.C .; Добжанский, Феодосий (1958). Принципы генетики. Нью-Йорк: Макгроу-Хилл.
- ^ а б c d е Фишер, Р. А. (1999). Генетическая теория естественного отбора (редакция variorum). Оксфорд: Издательство Оксфордского университета. ISBN 0-19-850440-3.
- ^ а б Кокран, Уильям Г. (1977). Методы отбора проб (Третье изд.). Нью-Йорк: Джон Вили и сыновья.
- ^ Это описано ниже в разделе генотипических отклонений.
- ^ Оба используются обычно.
- ^ См. Предыдущие цитаты.
- ^ Аллард, Р. У. (1960). Принципы селекции растений. Нью-Йорк: Джон Вили и сыновья.
- ^ а б Это читается как «σ 2п и / или σ 2q". В качестве п и q являются дополнительными, σ 2п ≡ σ 2q и σ 2п = σ 2q.
- ^ а б c d е ж грамм час я Гордон, И. (2003). «Уточнения разделения инбредной генотипической дисперсии». Наследственность. 91 (1): 85–89. Дои:10.1038 / sj.hdy.6800284. PMID 12815457.
- ^ а б c d е ж грамм час я j Райт, Сьюэлл (1951). «Генетическая структура популяций». Анналы евгеники. 15 (4): 323–354. Дои:10.1111 / j.1469-1809.1949.tb02451.x. PMID 24540312.
- ^ Помните, что вопрос об авто / алло -зиготности может возникнуть только у гомологичный аллели (то есть А и А, или же а и а), а не для негомологичный аллели (А и а), который не может иметь такое же аллельное происхождение.
- ^ Обычно для этой величины используют «α», а не «β» (например, в уже цитированных ссылках). Последнее используется здесь, чтобы свести к минимуму любую путаницу с «а», которая часто встречается также в этих же уравнениях.
- ^ а б c d Мазер, Кеннет; Джинкс, Джон Л. (1971). Биометрическая генетика (2-е изд.). Лондон: Чепмен и Холл. ISBN 0-412-10220-Х. PMID 5285746.
- ^ По терминологии Мезера дробь перед буквой часть этикетки для компонента.
- ^ В каждой строке этих уравнений компоненты представлены в одинаковом порядке. Следовательно, вертикальное сравнение по компонентам дает определение каждого в различных формах. Таким образом, компоненты Мазера были переведены в фишерские символы, что облегчило их сравнение. Перевод также получен формально. См. Gordon 2003.
- ^ а б Ковариация - это совместная изменчивость между двумя наборами данных. Как и дисперсия, она основана на сумма перекрестных произведений (SCP) вместо СС. Отсюда ясно, что дисперсия - это не более чем особая форма ковариации.
- ^ Хейман, Б. И. (1960). «Теория и анализ диаллельного креста. III». Генетика. 45: 155–172.
- ^ Было замечено, что когда п = q, или когда d = 0, β [= a + (q-p) d] "сводится" к а. В таких обстоятельствах σ2А = σ2а-но только численно. Они до сих пор не становиться одна и та же личность. Это было бы похоже non sequitur к тому, что отмечалось ранее для «отклонений замещения», рассматриваемых как «доминирование» для генной модели.
- ^ Подтверждающие цитаты приводились уже в предыдущих разделах.
- ^ Фишер заметил, что эти остатки возникли из-за эффектов доминирования: но он воздержался от определения их как «дисперсии доминирования». (См. Предыдущие цитаты.) Снова вернитесь к предыдущим обсуждениям здесь.
- ^ При рассмотрении происхождения терминов: Фишер также предложил слово «дисперсия» для этой меры изменчивости. См. Fisher (1999), стр. 311 и Fisher (1918).
- ^ а б c d Снедекор, Джордж В .; Кокран, Уильям Г. (1967). Статистические методы (Шестое изд.). Эймс: Издательство государственного университета Айовы. ISBN 0-8138-1560-6.
- ^ а б c Kendall, M. G .; Стюарт, А. (1958). Продвинутая теория статистики. Том 1 (2-е изд.). Лондон: Чарльз Гриффин.
- ^ Это обычная практика нет иметь индекс экспериментальной дисперсии "ошибки".
- ^ В биометрии это коэффициент дисперсии, при котором часть выражается в виде доли от целого, то есть коэффициент детерминации. Такие коэффициенты используются, в частности, в регрессивный анализ. Стандартная версия регрессионного анализа анализ пути. Здесь стандартизация означает, что данные сначала были разделены на их собственные экспериментальные стандартные ошибки, чтобы унифицировать шкалы для всех атрибутов. Это генетическое использование является еще одним важным проявлением коэффициентов детерминации.
- ^ Гордон, И. Л .; Byth, D.E .; Валаам, Л. Н. (1972). «Дисперсия отношений наследуемости, оцененная по компонентам фенотипической дисперсии». Биометрия. 28 (2): 401–415. Дои:10.2307/2556156. JSTOR 2556156. PMID 5037862.
- ^ Дом М. Р. (2002). «Оценки повторяемости не всегда устанавливают верхний предел наследуемости». Функциональная экология. 16 (2): 273–280. Дои:10.1046 / j.1365-2435.2002.00621.x.
- ^ а б c d Ли, Чинг Чун (1977). Анализ пути - учебник (Второй тираж с исправлениями ред.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-X.
- ^ квадратный корень из их продукта
- ^ Морони, М.Дж. (1956). Факты с цифр (третье изд.). Хармондсворт: Книги Пингвина.
- ^ а б Draper, Norman R .; Смит, Гарри (1981). Прикладной регрессионный анализ (Второе изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 0-471-02995-5.
- ^ а б c d Валаам, Л. Н. (1972). Основы биометрии. Лондон: Джордж Аллен и Анвин. ISBN 0-04-519008-9.
- ^ В прошлом обе формы ковариации родитель-потомок применялись к этой задаче оценки час2, но, как отмечено в подразделе выше, только один из них (cov (MPO)) действительно уместно. В cov (PO) однако полезно для оценки ЧАС2 как показано в основном тексте ниже.
- ^ Обратите внимание, что тексты, игнорирующие компонент доминирования cov (HS), ошибочно предполагают, что rHS "приблизительно" (¼ ч2 ).
- ^ Причард, Джонатан К .; Пикрелл, Джозеф К .; Куп, Грэм (23 февраля 2010 г.). «Генетика адаптации человека: жесткие, мягкие и полигенные адаптации». Текущая биология. 20 (4): R208–215. Дои:10.1016 / j.cub.2009.11.055. ISSN 1879-0445. ЧВК 2994553. PMID 20178769.
- ^ Турчин, Майкл С .; Chiang, Charleston W. K .; Палмер, Камерон Д .; Шанкарараман, Шрирам; Райх, Дэвид; Консорциум по генетическим исследованиям антропометрических признаков (GIANT); Хиршхорн, Джоэл Н. (сентябрь 2012 г.). «Свидетельства широко распространенного отбора вариаций стояния в Европе по SNP, связанным с ростом». Природа Генетика. 44 (9): 1015–1019. Дои:10,1038 / нг. 2368. ISSN 1546-1718. ЧВК 3480734. PMID 22902787.
- ^ Берг, Джереми Дж .; Куп, Грэм (август 2014). «Популяционно-генетический сигнал полигенной адаптации». PLOS Genetics. 10 (8): e1004412. Дои:10.1371 / journal.pgen.1004412. ISSN 1553-7404. ЧВК 4125079. PMID 25102153.
- ^ Поле, Яир; Бойл, Эван А .; Телис, Натали; Гао, Цзыюэ; Голтон, Кайл Дж .; Голан, Дэвид; Йенго, Лоик; Рошело, Гислен; Фрогель, Филипп (11 ноября 2016 г.). «Обнаружение адаптации человека за последние 2000 лет». Наука. 354 (6313): 760–764. Bibcode:2016Научный ... 354..760F. Дои:10.1126 / science.aag0776. ISSN 0036-8075. ЧВК 5182071. PMID 27738015.
- ^ Теоретически хвост бесконечный, но на практике есть квазиконец.
- ^ а б Беккер, Уолтер А. (1967). Руководство по процедурам количественной генетики (Второе изд.). Пуллман: Университет штата Вашингтон.
- ^ Обратите внимание, что это б2 это коэффициент отцовства (жAA) из Анализ родословной переписан с «уровнем поколения» вместо «А» в круглых скобках.
- ^ Небольшое "колебание" возникает из-за того, что б2 меняется на одно поколение позади а2- изучить их уравнения инбридинга.
- ^ Оценивается как квадратный корень из их произведения.
дальнейшее чтение
- Falconer DS и Mackay TFC (1996). Введение в количественную генетику, 4-е издание. Лонгман, Эссекс, Англия.
- Линч М. и Уолш Б. (1998). Генетика и анализ количественных признаков. Синауэр, Сандерленд, Массачусетс.
- Рофф Д.А. (1997). Эволюционная количественная генетика. Чепмен и Холл, Нью-Йорк.
- Сейкора, Тони. Зоотехния 3221 Животноводство. Tech. Миннеаполис: Университет Миннесоты, 2011. Печать.
внешняя ссылка
| Викискладе есть медиафайлы по теме Количественная генетика. |
- Уравнение заводчика
- Количественные генетические ресурсы к Майкл Линч и Брюс Уолш, включая два тома их учебника, Генетика и анализ количественных признаков и Эволюция и выбор количественных признаков.
- Ресурсы по Ник Бартон и другие.. из учебника, Эволюция.
- G-Matrix онлайн

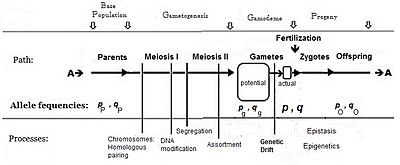

![{ textstyle [p ^ {2} (1-f) + pf]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f1f42f5a9c30f57d018ee039f24e662ebeafb72)

![{ textstyle [д ^ {2} (1-е) + дф]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03c693d0435f960d467b31a0d257d1ac8c647390)













![{ Displaystyle { begin {align} G_ {f} & = a (qp) + [2pqd-f (2pqd)] & = a (pq) + (1-f) 2pqd & = G_ {0 } -f 2pqd end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b62dfeae280dc4f4e334a3478d8481ca3b464b)






















![{ displaystyle sigma _ {t} ^ {2} = p_ {g} q_ {g} left [1- left (1- Delta f right) ^ {t} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e55f249d313eb204b0aad0fdd43789c5c9162df)













![{ textstyle f_ {t} = Delta f left [1 + f_ {t-1} left (2N-1 right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17a24c2fb8d160fe93430b166097b4cc095d60ad)


![{ Displaystyle влево (1-е вправо) влево [р_ {0} + q_ {0} вправо] ^ {2} = влево (1-е вправо) влево [р_ {0} ^ { 2} + q_ {0} ^ {2} right] + left (1-f right) left [2p_ {0} q_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/991c1f0545c26c29bd5dc324a08fd084d599990d)


![{ textstyle left [ left (1-е право) p_ {0} ^ {2} + fp_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c68483dd44cb95ca503376fb095d8cba86179be)
![{ textstyle left [ left (1-е право) q_ {0} ^ {2} + fq_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087333e8a96612e7fb9b5c5da00ac55b23584278)






![{ textstyle p_ {0} ^ {2} -f left [p_ {0} left (1-q_ {0} right) -p_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f31341803ce88db781b4f1c1fdc94e7a19a81488)

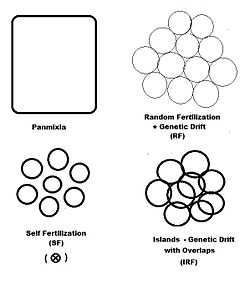








![{ displaystyle m_ {t} = 1- left [{ frac {2N {^ { mathsf {Islands}} Delta f_ {t}}} { left (2N-1 right) {^ { mathsf {острова}} Delta f_ {t} +1}}} right] ^ { tfrac {1} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a63b7a6c5b54623d679828146c2530268c3193c)





![{ Displaystyle бета _ {A} = д влево [а + влево (д-р вправо) д вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a8cb74299e659b83fc9cc07fe4056495b026ed)
![{ Displaystyle бета _ {а} = - п влево [а + влево (д-р вправо) д вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aedc78c372df5239f7f7ef9b28f19c8766374064)









![{ Displaystyle { begin {align} sigma _ {G} ^ {2} & = 2pq left [a + (qp) d right] ^ {2} + left (2pq right) ^ {2} d ^ {2} & = sigma _ {A} ^ {2} + sigma _ {D} ^ {2} & = left [ left ( sigma _ {a} ^ {2} + { mathsf {cov}} _ {ad} + sigma _ {d} ^ {2} right) right] + left [2pq sigma _ {d} ^ {2} right] end { выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c33eb29c59ac7394562c287f1b65e8d3fea9a8d7)


![{ displaystyle sigma _ {G_ {f}} ^ {2} = left (1-f right) sigma _ {G_ {0}} ^ {2} + f sigma _ {G_ {1} } ^ {2} + f left (1-f right) left [G_ {0} -G_ {1} right] ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baa52231a4dac02644cad91c045a5eb586f2502d)






![{ displaystyle sigma _ {G_ {f}} ^ {2} = left (1-f right) left [ sigma _ {A_ {0}} ^ {2} + sigma _ {D_ {0 }} ^ {2} right] + f left (4pq a ^ {2} right) + f left (1-f right) left [2pq d right] ^ {2} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8e77c382254b7230fcc0cb09f36d8a056cba93a)
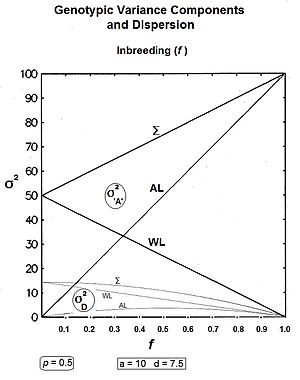







![{ displaystyle { begin {align} H ^ {2} & = { frac { sigma _ {G} ^ {2}} { sigma _ {P} ^ {2}}} & = { frac { sigma _ {A} ^ {2} + sigma _ {D} ^ {2}} { sigma _ {P} ^ {2}}} & = { frac { left [ sigma _ {a} ^ {2} + sigma _ {d} ^ {2} + cov_ {ad} right] + sigma _ {D} ^ {2}} { sigma _ {P} ^ {2} }} end {выровнены}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76a552eecb057ebb771e98bc0b94b39ed29de3c3)