WikiDer > Модель неба Рэлея - Википедия
Эта статья может требовать уборка встретиться с Википедией стандарты качества. (Сентябрь 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В Модель неба Рэлея описывает наблюдаемые поляризация узор дня небо. В атмосфере Рэлеевское рассеяние из свет с воздуха молекулы, вода, пыль и аэрозоли причины свет неба иметь определенную диаграмму поляризации. Такой же упругое рассеяние процессы делают небо синим. Поляризация характеризуется на каждом длина волны своим степень поляризации, и ориентация (угол e-вектора или угол рассеяния).
Картина поляризации неба зависит от небесное положение солнца. В то время как весь рассеянный свет до некоторой степени поляризован, свет сильно поляризован под углом рассеяния 90 ° от источника света. В большинстве случаев источником света является солнце, но и луна создает такой же узор. Степень поляризации сначала увеличивается с увеличением расстояния от Солнца, а затем уменьшается по мере удаления от Солнца. Таким образом, максимальная степень поляризации возникает в круговой полосе, расположенной под углом 90 ° от Солнца. В этом диапазоне обычно достигается степень поляризации около 80%.

Когда солнце находится на зенитполоса максимальной поляризации огибает горизонт. Свет с неба поляризован горизонтально вдоль горизонта. В течение сумерки в весенний или осенний период равноденствие, полоса максимальной поляризации определяется плоскостью Север-Зенит-Юг, или меридиан. В частности, поляризация вертикальна на горизонте на севере и юге, где меридиан пересекает горизонт. Поляризация в сумерках в равноденствие представлена цифрой справа. Красная полоса представляет собой круг в плоскости Север-Зенит-Юг, где небо сильно поляризовано. В стороны света N, E, S, W показаны у отметок 12 часов, 9 часов, 6 часов и 3 часов (против часовой стрелки вокруг небесная сфера поскольку наблюдатель смотрит в небо).
Обратите внимание: поскольку картина поляризации зависит от солнца, она меняется не только в течение дня, но и в течение года. Зимой, когда солнце садится к югу, плоскость Север-Зенит-Юг смещается, при этом «эффективный» север фактически расположен несколько к западу. Таким образом, если солнце садится под азимутом 255 ° (15 ° к югу от запада), диаграмма поляризации будет максимальной вдоль горизонта с азимутом 345 ° (15 ° к западу от севера) и 165 ° (15 ° к востоку от Юг).
В течение одного дня узор вращается вместе с изменением положения солнца. В сумерках он обычно появляется примерно за 45 минут до местного восхода солнца и исчезает через 45 минут после местного заката. После установки он очень стабилен, показывая изменения только в его вращении. Его легко увидеть в любой день в поляризованных солнцезащитных очках.
Многие животные используют поляризационные модели неба в сумерках и в течение дня как навигация инструмент. Поскольку он определяется исключительно положением солнца, его легко использовать в качестве компаса для ориентации животных. Ориентируясь по шаблонам поляризации, животные могут определять местонахождение солнца и, таким образом, определять его стороны света.
Теория
Геометрия
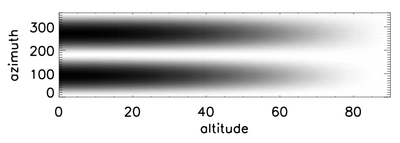
Геометрия поляризации неба может быть представлена в виде небесного треугольника, основанного на Солнце, зените и наблюдаемом наведении (или точке рассеяния). В модели γ - угловое расстояние между наблюдаемым наведением и солнцем, Θs - зенитное расстояние Солнца (90 ° - высота Солнца), Θ - угловое расстояние между наблюдаемым наведением и зенитом (90 ° - наблюдаемая высота), Φ - угол между направлением зенита и направлением Солнца в наблюдаемом наведении, и ψ - угол между направлением на Солнце и наблюдаемым направлением в зенит.
Таким образом, сферический треугольник определяется не только тремя точками, расположенными на Солнце, зените и наблюдаемой точке, но и тремя внутренними углами, а также тремя угловыми расстояниями. В высота-азимут сетка угловое расстояние между наблюдаемым наведением и солнцем и угловое расстояние между наблюдаемым наведением и зенитом изменяются, в то время как угловое расстояние между солнцем и зенитом остается постоянным в один момент времени.
На рисунке слева показаны два изменяющихся угловых расстояния, отображенные на сетке высоты и азимута (с высотой, расположенной на оси x, и азимутом, расположенным на оси y). На верхнем графике показано изменение углового расстояния между наблюдаемым направлением и солнцем, которое противоположно внутреннему углу, расположенному в зените (или углу рассеяния). Когда Солнце находится в зените, это расстояние является наибольшим вдоль горизонта во всех сторонах света. Затем он уменьшается с увеличением высоты, приближаясь к зениту. В сумерках солнце садится на западе. Следовательно, расстояние наибольшее, если смотреть прямо в сторону от солнца вдоль горизонта на востоке, и наименьшее - вдоль горизонта на западе.
Нижний график на рисунке слева представляет угловое расстояние от наблюдаемой точки до зенита, который противоположен внутреннему углу, расположенному на Солнце. В отличие от расстояния между наблюдаемым наведением и солнцем, оно не зависит от азимута, то есть кардинального направления. Просто она больше всего на горизонте на малых высотах и линейно уменьшается с увеличением высоты.
Цифра справа представляет три угловых расстояния. Левый представляет угол в наблюдаемой точке между зенитным направлением и солнечным направлением. Таким образом, это сильно зависит от изменения направления Солнца, когда солнце движется по небу. Средний представляет собой угол на солнце между зенитным направлением и указателем. Опять же, это сильно зависит от изменения направления. Это симметрично между Северным и Южным полушариями. Правый представляет угол в зените между направлением на Солнце и указателем. Таким образом, он вращается вокруг небесной сферы.
Степень поляризации
Модель неба Рэлея предсказывает степень поляризации неба в качестве:
В качестве простого примера можно отобразить степень поляризации на горизонте. Как видно на рисунке справа, она высока на севере (0 ° и 360 °) и на юге (180 °). Затем он напоминает функцию косинуса и уменьшается к востоку и западу, достигая нуля в этих основных направлениях.
Степень поляризации легко понять, если нанести на карту высотно-азимутальную сетку, как показано ниже. Когда солнце садится строго на запад, максимальная степень поляризации видна в плоскости Север-Зенит-Юг. Вдоль горизонта на высоте 0 ° он самый высокий на севере и юге и самый низкий на востоке и западе. Затем по мере приближения высоты к зениту (или плоскости максимальной поляризации) поляризация остается высокой на севере и юге и увеличивается до тех пор, пока снова не станет максимальной на 90 ° на востоке и западе, где она будет затем в зените и в пределах плоскость поляризации.
Щелкните соседнее изображение, чтобы просмотреть анимацию, которая представляет степень поляризации, показанную на небесной сфере. Черный цвет представляет области, где степень поляризации равна нулю, тогда как красный цвет представляет области, где степень поляризации намного больше. Это примерно 80%, что является реалистичным максимумом для ясного рэлеевского неба в дневное время. Таким образом, видео начинается, когда солнце находится немного выше горизонта под азимутом 120 °. Небо сильно поляризовано в эффективной плоскости Север-Зенит-Юг. Это немного смещено, потому что азимут солнца не направлен на восток. Солнце движется по небу, окружая его четкими круговыми поляризационными узорами. Когда солнце находится в зените, поляризация не зависит от азимута и уменьшается с увеличением высоты (по мере приближения к солнцу). Затем картина продолжается, когда солнце снова приближается к горизонту для заката. Видео заканчивается тем, что солнце скрывается за горизонтом.
Угол поляризации
Плоскость рассеяния - это плоскость, проходящая через Солнце, наблюдателя и наблюдаемую точку (или точку рассеяния). Угол рассеяния γ - это угловое расстояние между Солнцем и наблюдаемой точкой. Уравнение для угла рассеяния выводится из закон косинусов к сферическому треугольнику (см. рисунок выше в разделе геометрии). Выдается:
В приведенном выше уравнении ψs и θs - соответственно азимут и зенитный угол Солнца, а ψ и θ - соответственно азимут и зенитный угол наблюдаемой точки.
Это уравнение распадается в зените, где угловое расстояние между наблюдаемым наведением и зенитом, θs равно 0. Здесь ориентация поляризации определяется как разница в азимуте между наблюдаемым наведением и солнечным азимутом.
Угол поляризации (или угол поляризации) определяется как относительный угол между вектором, касательным к меридиану наблюдаемой точки, и углом, перпендикулярным плоскости рассеяния.
Углы поляризации показывают регулярный сдвиг угла поляризации с азимутом. Например, когда солнце садится на западе, углы поляризации продолжаются вокруг горизонта. В это время степень поляризации постоянна в круговых полосах с центром вокруг Солнца. Таким образом, степень поляризации, а также соответствующий ей угол явно смещаются вокруг горизонта. Когда солнце находится в зените, горизонт представляет собой постоянную степень поляризации. Соответствующий угол поляризации по-прежнему смещается в разные стороны к зениту из разных точек.
Видео справа представляет угол поляризации, нанесенный на небесную сферу. Он начинается с Солнца, расположенного аналогичным образом. Угол равен нулю по линии от солнца к зениту и увеличивается по часовой стрелке к востоку, когда наблюдаемая точка перемещается по часовой стрелке к востоку. Когда солнце встает на востоке, угол действует аналогичным образом, пока солнце не начинает двигаться по небу. Когда солнце движется по небу, угол равен нулю и высок вдоль линии, определяемой солнцем, зенитом и антисолнцем. Это ниже к югу от этой линии и выше к северу от этой линии. Когда солнце находится в зените, угол либо полностью положительный, либо 0. Эти два значения вращаются в сторону запада. Затем видео повторяется аналогичным образом, когда солнце садится на западе.
Q- и U-параметры Стокса
Угол поляризации можно развернуть на Q и U Параметры Стокса. Q и U определяются как линейно поляризованные интенсивности вдоль позиционных углов 0 ° и 45 ° соответственно; -Q и -U находятся по позиционным углам 90 ° и -45 °.
Если солнце расположено на горизонте строго на запад, тогда степень поляризации будет вдоль плоскости Север-Зенит-Юг. Если наблюдатель смотрит на Запад и смотрит в зенит, поляризация горизонтальна относительно наблюдателя. В этом направлении Q равно 1, а U равно 0. Если наблюдатель все еще смотрит на запад, но вместо этого смотрит на север, то поляризация вертикальна по отношению к нему. Таким образом, Q равно -1, а U остается 0. Вдоль горизонта U всегда 0. Q всегда -1, за исключением Востока и Запада.
Угол рассеяния (угол в зените между направлением на Солнце и направлением наблюдателя) вдоль горизонта представляет собой круг. С востока через запад он равен 180 °, а с запада через восток - 90 ° в сумерках. Когда солнце садится на западе, угол составляет 180 ° с востока на запад и только 90 ° с запада на восток. Угол рассеяния на высоте 45 ° постоянный.
Входные параметры стоксов q и u тогда относятся к северу, но в системе отсчета высоты и азимута. Мы можем легко развернуть q, предполагая, что он находится в направлении + altitude. Из основного определения мы знаем, что + Q - это угол 0 °, а -Q - угол 90 °. Следовательно, Q вычисляется по синусоидальной функции. Аналогичным образом U рассчитывается из функции косинуса. В угол поляризации всегда перпендикулярна плоскости рассеяния. Следовательно, к обоим углам рассеяния добавляется 90 °, чтобы найти углы поляризации. Отсюда определяются Q- и U-параметры Стокса:
и
Угол рассеяния, полученный из закона косинусов, относится к Солнцу. Угол поляризации - это угол относительно зенита или положительной высоты. Есть линия симметрии, определяемая солнцем и зенитом. Он проходит от Солнца через зенит к другой стороне небесной сферы, где могло бы быть «антисолнце». Это также эффективный самолет Восток-Зенит-Запад.
Первое изображение справа представляет вход q, нанесенный на небесную сферу. Он симметричен относительно линии, определяемой солнцем-зенит-антисолнцем. В сумерках в плоскости Север-Зенит-Юг он отрицательный, потому что он вертикален со степенью поляризации. Она горизонтальна или положительна в плоскости Восток-Зенит-Запад. Другими словами, она положительна в направлении ± высоты и отрицательна в направлении ± азимута. Когда солнце движется по небу, значение q остается высоким вдоль линии солнце-зенит-антисолнце. Он остается нулевым по кругу, основанному на Солнце и зените. Проходя зенит, он поворачивается к югу и повторяет ту же схему до заката.
Второе изображение справа представляет вход u, нанесенный на небесную сферу. Параметр u-Стокса меняет знаки в зависимости от того, в каком квадранте он находится. Четыре квадранта определяются линией симметрии, эффективной плоскостью Восток-Зенит-Запад и плоскостью Север-Зенит-Юг. Он не симметричен, потому что определяется углами ± 45 °. В некотором смысле он образует два круга вокруг линии симметрии, а не только один.
Это легко понять, если сравнить с вводом q. Если вход q находится на полпути между 0 ° и 90 °, вход u либо положительный при + 45 °, либо отрицательный при -45 °. Аналогично, если вход q положительный при 90 ° или отрицательный при 0 °, вход u находится на полпути между + 45 ° и -45 °. Это видно по несимметричным кружкам вокруг линии симметрии. Затем он следует той же схеме по небу, что и ввод q.
Нейтральные точки и линии
Области, где степень поляризации равна нулю (световой люк неполяризован), называются нейтральными точками. Здесь параметры Стокса Q и U также равны нулю по определению. Следовательно, степень поляризации увеличивается с увеличением расстояния от нейтральных точек.
Эти условия выполняются в нескольких определенных местах на небе. Точка Араго расположена выше антисолнечной точки, а точки Бабине и Брюстера расположены выше и ниже Солнца соответственно. Зенитное расстояние точек Бабине или Араго увеличивается с увеличением зенитного расстояния Солнца. Эти нейтральные точки могут отклоняться от своих обычных положений из-за помех от пыли и других аэрозолей.
Поляризация светового люка переключается с отрицательной на положительную при прохождении нейтральной точки параллельно солнечному или антисолнечному меридиану. Линии, разделяющие области положительного Q и отрицательного Q, называются нейтральными линиями.
Деполяризация
Небо Рэлея вызывает четко выраженную картину поляризации во многих различных обстоятельствах. Однако степень поляризации не всегда остается постоянной и может уменьшаться в различных ситуациях. Небо Рэлея может подвергнуться деполяризации из-за близлежащих объектов, таких как облака и большие отражающие поверхности, такие как океан. Он также может меняться в зависимости от времени суток (например, в сумерках или ночью).
Ночью поляризация залитого лунным светом неба очень сильно снижается при наличии городской световое загрязнение, потому что рассеянный городской свет не сильно поляризован.[2]
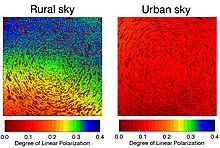
Обширные исследования показывают, что угол поляризации в ясном небе сохраняется под облаками, если воздух под облаком напрямую освещен солнцем. Рассеяние прямых солнечных лучей этими облаками приводит к той же картине поляризации. Другими словами, пропорция неба, соответствующая модели неба Рэлея, высока как для ясного, так и для облачного неба. Узор также хорошо виден на небольших видимых участках неба. Небесный угол поляризации не зависит от облаков.
Шаблоны поляризации остаются неизменными, даже если на небе нет солнца. Образцы сумерек создаются в период времени между началом астрономических сумерек (когда солнце находится на 18 ° ниже горизонта) и восходом или закатом и концом астрономических сумерек. Продолжительность астрономических сумерек зависит от длины пути, пройденного солнцем за горизонтом. Таким образом, это зависит от времени года, а также от местоположения, но может длиться до 1,5 часов.
Картина поляризации, вызванная сумерками, остается довольно постоянной в течение этого периода времени. Это связано с тем, что солнце движется ниже горизонта почти перпендикулярно ему, и поэтому его азимут изменяется очень медленно в течение этого периода времени.
В сумерках рассеянный поляризованный свет исходит из верхних слоев атмосферы, а затем проходит через всю нижнюю атмосферу, прежде чем достигнет наблюдателя. Это обеспечивает множественные возможности рассеяния и вызывает деполяризацию. Было замечено, что поляризация увеличивается примерно на 10% от наступления сумерек до рассвета. Таким образом, картина остается неизменной, а степень немного меняется.
Не только модели поляризации остаются неизменными, когда солнце движется по небу, но и когда луна движется по небу ночью. Луна создает такую же картину поляризации. Таким образом, можно использовать поляризационные диаграммы в качестве инструмента для навигации в ночное время. Единственная разница в том, что степень поляризации не такая сильная.
Основные свойства поверхности могут влиять на степень поляризации дневного неба. Степень поляризации сильно зависит от свойств поверхности. По мере увеличения отражательной способности поверхности или оптической толщины степень поляризации уменьшается. Следовательно, небо Рэлея у океана может быть сильно деполяризованным.
Наконец, в рэлеевском рассеянии наблюдается четкая зависимость от длины волны. Он наиболее высок на коротких волнах, тогда как поляризация светового люка наиболее высока на средних и длинных волнах. Первоначально он максимален в ультрафиолете, но по мере того, как свет движется к поверхности Земли и взаимодействует посредством многолучевого рассеяния, он становится высоким в диапазоне от средних до длинных волн. Угол поляризации не меняется в зависимости от длины волны.
Использует
Многие животные, обычно насекомые, чувствительны к поляризации света и поэтому могут использовать поляризационные модели дневного неба в качестве инструмента для навигации. Эта теория была впервые предложена Карл фон Фриш при взгляде на небесную ориентацию пчел. Картина естественной поляризации неба служит легко обнаруживаемым компасом. Судя по диаграммам поляризации, эти виды могут ориентироваться, определяя точное положение солнца без использования прямых солнечных лучей. Таким образом, под облачным небом или даже ночью животные могут найти дорогу.
Однако использование поляризованного света в качестве компаса - непростая задача. Животное должно уметь обнаруживать и анализировать поляризованный свет. Эти виды имеют специализированные фоторецепторы в их глазах, которые реагируют на ориентацию и степень поляризации вблизи зенита. Они могут извлекать информацию о интенсивность и ориентация степени поляризации. Затем они могут использовать это визуально, чтобы ориентироваться и распознавать различные свойства поверхностей.
Есть явные доказательства того, что животные могут ориентироваться даже в сумерках, когда солнце находится за горизонтом. Насколько хорошо насекомые могут ориентироваться с помощью ночных поляризационных моделей, все еще остается предметом исследования. Пока что известно, что у ночных сверчков есть датчики поляризации с широким полем поля, и они должны иметь возможность использовать ночные поляризационные диаграммы для ориентации. Также было замечено, что ночные перелетные птицы дезориентируются, когда картина поляризации в сумерках неясна.
Лучшим примером является пчела Megalopta genalis, который населяет тропические леса в Центральной Америке и собирает мусор до восхода и после захода солнца. Эта пчела покидает свое гнездо примерно за 1 час до восхода солнца, собирает корм до 30 минут и точно возвращается в гнездо до восхода солнца. Аналогично действует и сразу после захода солнца.
Таким образом, эта пчела является примером насекомого, которое может воспринимать поляризационные модели в астрономических сумерках.[3] Этот случай не только иллюстрирует тот факт, что поляризационные узоры присутствуют в сумерках, но и остается прекрасным примером того, что при неблагоприятных условиях освещения пчела ориентируется на себя на основе поляризационных узоров сумеречного неба.
Было высказано предположение, что Викинги могли ориентироваться в открытом море аналогичным образом, используя двулучепреломляющий кристалл Исландский лонжерон, который они назвали «солнечным камнем», чтобы определить ориентацию поляризации неба.[4][5][6][7][8] Это позволило бы навигатору определить местонахождение солнца, даже когда оно было закрыто облачным покровом. Реальный пример такого «солнечного камня» был найден на затонувшем (тюдоровском) корабле, датируемом 1592 годом, в непосредственной близости от навигационного оборудования корабля.[9]
Неполяризованные объекты
Как искусственные, так и естественные объекты в небе бывает очень сложно обнаружить, используя только интенсивность света. К таким объектам относятся облака, спутники и самолеты. Однако поляризация этих объектов из-за резонансной рассеяние, выброс, отражение, или другие явления могут отличаться от фонового освещения. Таким образом, их можно легче обнаружить с помощью поляризационного изображения. Существует широкий выбор дистанционное зондирование приложения, в которых поляризация полезна для обнаружения объектов, которые иначе трудно увидеть.
Примечания и ссылки
- Поляризационные картины сумеречного неба. Кронин Т.В. и др., 2005, SPIE, 5888, 389
- Поляризационные картины летнего неба и его нейтральные точки, измеренные с помощью поляриметрии полного неба в финской Лапландии к северу от Полярного круга. Gál J. et al. 2001, Proc. R. Soc. Лондон. 457, 1385
- Измерение распределения поляризованного сияния в крыше. Лю Ю. и Восс К., 1997, ApOpt, 36, 8753
- Как угол поляризации при ясном небе продолжается под облаками: измерения на всем небе и их значение для ориентации животных. Pomozi, I. et al., 2001, J. Exp. Биол., 204, 2933
- ^ Колсон, Кинселл (1988). Поляризация и интенсивность света в атмосфере.. A. Deepak Pub.
- ^ Kyba, C. C. M .; Ruhtz, T .; Фишер, Дж .; Хёлькер, Ф. (17 декабря 2011 г.). «Сигнал поляризации лунного фонаря, загрязненный городским освещением». Журнал геофизических исследований. 116 (D24): н / д. Bibcode:2011JGRD..11624106K. Дои:10.1029 / 2011JD016698.
- ^ Cronin, T.W .; Warrant, E.J .; Грейнер, Б. (2006). "Небесные поляризационные картины в сумерках". Appl. Опт. 45 (22): 5582. Bibcode:2006ApOpt..45.5582C. Дои:10.1364 / АО.45.005582. PMID 16855654.
- ^ Сухай, Б .; Хорват, Г. (2004). «Насколько хорошо модель Рэлея описывает распределение E-вектора света в крыше в ясных и облачных условиях? Поляриметрическое исследование всего неба». JOSA A. 21 (9): 1669. Bibcode:2004JOSAA..21.1669S. Дои:10.1364 / josaa.21.001669.
- ^ Солнечный камень викингов, с сайта Polarization.net. Проверено 8 февраля 2007 года.
- ^ Тайны навигаторов викингов, Лейф К. Карлсен. One Earth Press, 2003. ISBN 978-0-9721515-0-4
- ^ Могли ли викинги перемещаться в условиях тумана и облачности за счет поляризации окна в крыше? Об атмосферно-оптических предпосылках поляриметрической навигации викингов в условиях туманного и облачного неба Рамон Хегедюс и др.[1]
- ^ Хорват, Г. и др. (2011). «По следам викингов с поляризованным просветом: экспериментальное исследование оптических условий атмосферы, позволяющих поляриметрическую навигацию моряками викингов» Фил. Пер. R. Soc. B (2011) 366, 772–782 DOI: 10.1098 / rstb.2010.0194
- ^ Уэйд, Лиззи (5 марта 2013 г.). "Солнечный камень, обнаруженный при кораблекрушении". Наука. Американская ассоциация развития науки. Архивировано из оригинал 9 марта 2013 г.. Получено Одиннадцатое марта, 2013.