WikiDer > Алгоритм обратного удаления
| График и дерево алгоритмы поиска |
|---|
| Списки |
| похожие темы |
В алгоритм обратного удаления является алгоритм в теория графов используется для получения минимальное остовное дерево из данного подключенного, реберно-взвешенный граф. Впервые он появился в Крускал (1956), но его не следует путать с Алгоритм Краскала который появляется в той же статье. Если граф отключен, этот алгоритм найдет минимальное остовное дерево для каждой отключенной части графа. Набор этих минимальных остовных деревьев называется минимальным остовным лесом, который содержит каждую вершину в графе.
Этот алгоритм представляет собой жадный алгоритм, выбирая лучший выбор в любой ситуации. Это наоборот Алгоритм Краскала, который представляет собой еще один жадный алгоритм поиска минимального остовного дерева. Алгоритм Краскала начинается с пустого графа и добавляет ребра, в то время как алгоритм обратного удаления начинается с исходного графа и удаляет ребра из него. Алгоритм работает следующим образом:
- Начнем с графа G, который содержит список ребер E.
- Пройдите через E в порядке убывания веса ребер.
- Для каждого ребра проверьте, приведет ли удаление ребра к дальнейшему отключению графа.
- Выполните любое удаление, не приводящее к дополнительному отключению.
Псевдокод
функция ReverseDelete (края [] E) является Сортировать E в порядке убывания Определите индекс я ← 0 пока я < размер(E) делать Определять край ← E[я] Удалить E[я] если график не связан тогда E[я] ← край я ← я + 1 возвращаться края [] E
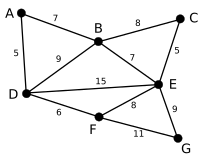
В приведенном выше графике есть множество ребер E с каждым ребром, содержащим вес, и связанные вершины v1 и v2.
Пример
В следующем примере зеленые края оцениваются алгоритмом, а красные края удалены.
Продолжительность
Можно показать, что алгоритм работает в О(E бревно V (журнал журнала V)3) время (используя нотация big-O), куда E количество ребер и V количество вершин. Эта оценка достигается следующим образом:
- Сортировка краев по весу с использованием сравнительной сортировки требует О(E бревно E) время, которое можно упростить до О(E бревно V) используя тот факт, что наибольшая E может быть это V2.
- Есть E итерации цикла.
- Удаление ребра, проверка связности результирующего графа и (если он отключен) повторная вставка ребра могут быть выполнены в О(бревноV (журнал журнала V)3) время на операцию (Thorup 2000).
Доказательство правильности
Рекомендуется ознакомиться с доказательством Алгоритм Краскала первый.
Доказательство состоит из двух частей. Во-первых, доказывается, что ребра, оставшиеся после применения алгоритма, образуют остовное дерево. Во-вторых, доказано, что остовное дерево имеет минимальный вес.
Остовное дерево
Оставшийся подграф (g), созданный алгоритмом, не отсоединяется, так как алгоритм проверяет это в строке 7. Результирующий подграф не может содержать цикл, поскольку в этом случае при движении по ребрам мы столкнемся с максимальным ребром в цикле, и мы удалим это ребро. Таким образом, g должно быть остовным деревом основного графа G.
Минимальность
Покажем, что следующее предложение п истинно по индукции: если F - это множество ребер, оставшихся в конце цикла while, то существует некоторое минимальное остовное дерево, которое (его ребра) являются подмножеством F.
- Четко п удерживается перед началом цикла while. поскольку взвешенный связный граф всегда имеет минимальное остовное дерево и поскольку F содержит все ребра графа, то это минимальное остовное дерево должно быть подмножеством F.
- Теперь предположим п верно для некоторого неокончательного набора ребер F и разреши Т быть минимальным остовным деревом, которое содержится в Ф. мы должны показать, что после удаления ребра e в алгоритме существует некоторое (возможно, другое) остовное дерево T ', которое является подмножеством F.
- если следующее удаленное ребро e не принадлежит T, то T = T 'является подмножеством F и п держит. .
- в противном случае, если e принадлежит T: сначала обратите внимание, что алгоритм удаляет только те ребра, которые не вызывают разъединения в F., поэтому e не вызывает разъединения. Но удаление e вызывает отключение в дереве T (так как оно является членом T). Предположим, что e разделяет T на подграфы t1 и t2. Поскольку весь граф связан после удаления e, тогда должен существовать путь между t1 и t2 (кроме e), поэтому должен существовать цикл C в F (до удаления e). теперь у нас должно быть другое ребро в этом цикле (назовем его f), которое не находится в T, но находится в F (поскольку, если бы все ребра цикла были в дереве T, то оно больше не было бы деревом). Теперь мы утверждаем, что T '= T - e + f - минимальное остовное дерево, являющееся подмножеством F.
- сначала докажем, что T '- остовное дерево . мы знаем, что удаляя ребро в дереве и добавляя другое ребро, которое не вызывает цикла, мы получаем другое дерево с теми же вершинами. так как T было остовным деревом, то T 'должно быть остовное дерево тоже. так как добавление «f» не вызывает никаких циклов, поскольку «e» удаляется (обратите внимание, что дерево T содержит все вершины графа).
- во-вторых, мы доказываем, что T 'является минимум остовное дерево. у нас есть три случая для ребер «e» и «f». wt - весовая функция.
- wt (f)
- wt (f)> wt (e) это тоже невозможно. с тех пор, когда мы проходим ребра в порядке убывания их весов, мы должны сначала увидеть "f". так как у нас есть цикл C, удаление "f" не вызовет разъединения в F., поэтому алгоритм удалил бы его из F раньше. поэтому "f" не существует в F, что невозможно (мы доказали, что f существует на шаге 4.
- так wt (f) = wt (e), так что T 'также минимум остовное дерево. так снова п держит.
- wt (f)
- так п выполняется, когда цикл while завершен (то есть когда мы видели все ребра), и мы доказали, что в конце F становится остовное дерево и мы знаем, что у F есть минимум остовное дерево как его подмножество. так что F должен быть минимальное остовное дерево сам .
Смотрите также
Рекомендации
- Клейнберг, Джон; Тардос, Ива (2006), Разработка алгоритма, Нью-Йорк: Pearson Education, Inc..
- Крускал, Джозеф Б. (1956), «О кратчайшем остовном поддереве графа и проблеме коммивояжера», Труды Американского математического общества, 7 (1): 48–50, Дои:10.2307/2033241, JSTOR 2033241.
- Торуп, Миккель (2000), "Почти оптимальная полностью динамическая связность графов", Proc. 32-й симпозиум ACM по теории вычислений, стр. 343–350, Дои:10.1145/335305.335345.