WikiDer > Линейчатая поверхность

Определение линейчатой ​​поверхности: каждая точка лежит на прямой

В геометрия, а поверхность S является управлял (также называемый прокрутка) если через каждую точку S есть прямая линия, которая лежит на S. Примеры включают самолет, боковая поверхность цилиндр или же конус, а коническая поверхность с эллиптический директриса, то правый коноид, то геликоид, а касательная разворачивающаяся гладкой изгиб в космосе.

Линейчатую поверхность можно описать как набор точек, проходящих по движущейся прямой. Например, конус формируется путем фиксации одной точки линии при перемещении другой точки вдоль линии. круг. Поверхность дважды управляемый если через каждую из его точек проходят две различные прямые, лежащие на поверхности. В гиперболический параболоид и гиперболоид одного листа являются двояковыпуклыми поверхностями. Плоскость - единственная поверхность, которая содержит не менее трех различных линий, проходящих через каждую из своих точек (Фукс и Табачников 2007).

Свойства быть управляемым или дважды управляемым сохраняются проективные карты, и поэтому являются концепциями проективная геометрия. В алгебраической геометрии линейчатые поверхности иногда рассматриваются как поверхности в аффинном или проективном пространстве над полем, но они также иногда рассматриваются как абстрактные алгебраические поверхности без вложения в аффинное или проективное пространство, и в этом случае «прямая линия» означает аффинная или проективная линия.

Определение и параметрическое представление

Линейчатая поверхность, образованная двумя кривыми Безье как направляющими (красный, зеленый)

Двумерный дифференцируемое многообразие называется линейчатая поверхность, если это союз однопараметрического семейства линий. Линии этого семейства являются генераторы линейчатой ​​поверхности.

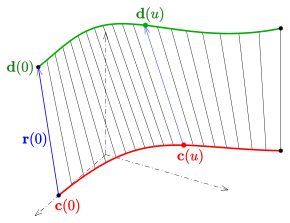
Линейчатая поверхность может быть описана параметрическое представление формы

• (CR) ${ displaystyle quad mathbf {x} (u, v) = { color {красный} mathbf {c} (u)} + v ; { color {blue} mathbf {r} (u)} , v in mathbb {R} ,}$.

Любая кривая ${ Displaystyle ; v mapsto mathbf {x} (u_ {0}, v) ;}$ с фиксированным параметром ${ displaystyle u = u_ {0}}$ образующая (линия) и кривая ${ Displaystyle ; и mapsto mathbf {c} (и) ;}$ это директриса представительства. Векторы ${ Displaystyle ; mathbf {r} (и) neq { bf {0 ;}}}$ Опишите направления генераторов.

Директриса может свернуться в точку (в случае конуса см. Пример ниже).

В качестве альтернативы линейчатая поверхность (CR) можно описать

• (CD) ${ displaystyle quad mathbf {x} (u, v) = (1-v) ; { color {красный} mathbf {c} (u)} + v ; { color {зеленый} mathbf {d} (u)} }$

со второй директрисой ${ Displaystyle ; mathbf {d} (u) = mathbf {c} (u) + mathbf {r} (u) ;}$.

Как вариант, можно начать с двух непересекающихся кривых. ${ Displaystyle mathbf {с} (и), mathbf {d} (и)}$ в качестве директрис и обойтись (CD) линейчатая поверхность с направлением линий ${ Displaystyle ; mathbf {r} (u) = mathbf {d} (u) - mathbf {c} (u) .}$

Для создания линейчатой ​​поверхности двумя направляющими (или одной направляющей и векторами направлений линий) важна не только геометрическая форма этих кривых, но и их специальные параметрические представления влияют на форму линейчатой ​​поверхности (см. Примеры ), г)).

Для представления теоретических исследований (CR) более выгодно, потому что параметр ${ displaystyle v}$ появляется только один раз.

Примеры

цилиндр, конус

а) Правый круговой цилиндр:

${ Displaystyle х ^ {2} + у ^ {2} = а ^ {2} }$:

${ displaystyle mathbf {x} (u, v) = (a cos u, a sin u, v) ^ {T}}$

${ displaystyle = { color {красный} (a cos u, a sin u, 0) ^ {T}} ; + ; v ; { color {blue} (0,0,1) ^ {T}}}$

${ displaystyle = (1-v) ; { color {red} (a cos u, a sin u, 0) ^ {T}} ; + ; v ; { color {green} ( a cos u, a sin u, 1) ^ {T}} .}$

с

${ displaystyle mathbf {c} (u) = (a cos u, a sin u, 0) ^ {T} , mathbf {r} (u) = (0,0,1) ^ { T} , mathbf {d} (u) = (a cos u, a sin u, 1) ^ {T} .}$

б) Правый круговой конус:

${ displaystyle x ^ {2} + y ^ {2} = z ^ {2} }$:

${ Displaystyle mathbf {х} (и, v) = ( соз и, грех и, 1) ^ {Т} ; + ; v ; ( соз и, грех и, 1) ^ { T}}$

${ Displaystyle = (1-v) ; ( соз и, грех и, 1) ^ {Т} ; + ; v ; (2 соз и, 2 грех и, 2) ^ {Т }.}$

с ${ displaystyle quad mathbf {c} (u) = ( cos u, sin u, 1) ^ {T} ; = ; mathbf {r} (u) , quad mathbf {d } (u) = (2 cos u, 2 sin u, 2) ^ {T} .}$
В этом случае можно было бы использовать вершину как направляющую, то есть: ${ Displaystyle mathbf {c} (u) = (0,0,0) ^ {T} }$ и ${ Displaystyle mathbf {г} (и) = ( соз и, грех и, 1) ^ {Т} }$ как направления линии.

Для любого конуса можно выбрать вершину в качестве направляющей. Этот случай показывает: Направляющая линейчатой ​​поверхности может вырождаться в точку.

геликоид

в) Геликоид:

${ Displaystyle mathbf {х} (и, v) = ; (v соз и, v грех и, ку) ^ {Т} ;}$

${ Displaystyle = ; (0,0, ку) ^ {T} ; + ; v ; ( соз и, грех и, 0) ^ {T} }$

${ displaystyle = ; (1-v) ; (0,0, ку) ^ {T} ; + ; v ; ( cos u, sin u, ku) ^ {T} .}$

Директриса ${ Displaystyle mathbf {с} (и) = (0,0, ку) ^ {Т} ;}$ ось z, направления линий ${ Displaystyle ; mathbf {г} (и) = ( соз и, грех и, 0) ^ {Т} ;}$ и вторая директриса ${ Displaystyle mathbf {d} (и) = ( соз и, грех и, ку) ^ {Т} }$ это спираль.

Геликоид - это частный случай линейчатые обобщенные геликоиды.

г) Цилиндр, конус и гиперболоиды:

гиперболоид одного листа для ${ displaystyle varphi = 63 ^ { circ}}$

Параметрическое представление

${ Displaystyle mathbf {х} (и, v) = (1-v) ; ( соз (и- varphi), sin (и- varphi), - 1) ^ {T} ; + ; v ; ( cos (u + varphi), sin (u + varphi), 1) ^ {T}}$

имеет два горизонтальных круга в качестве направляющих. Дополнительный параметр ${ displaystyle varphi}$ позволяет изменять параметрические представления окружностей. За

${ displaystyle varphi = 0 }$ каждый получает цилиндр ${ displaystyle x ^ {2} + y ^ {2} = 1}$, за

${ displaystyle varphi = pi / 2 }$ один получает конус ${ displaystyle x ^ {2} + y ^ {2} = z ^ {2}}$ и для

${ displaystyle 0 < varphi < pi / 2 }$ получается гиперболоид из одного листа с уравнением ${ displaystyle { tfrac {x ^ {2} + y ^ {2}} {a ^ {2}}} - { tfrac {z ^ {2}} {c ^ {2}}} = 1 }$ и полуоси ${ Displaystyle а = соз varphi ;, ; с = cot varphi}$.

Гиперболоид из одного листа - это вдвойне линейчатая поверхность.

Гиперболический параболоид

д) Гиперболический параболоид:

Если две директрисы в (CD) линии

${ displaystyle mathbf {c} (u) = (1-u) mathbf {a} _ {1} + u mathbf {a} _ {2}, quad mathbf {d} (u) = ( 1-u) mathbf {b} _ {1} + u mathbf {b} _ {2}}$

один получает

${ displaystyle mathbf {x} (u, v) = (1-v) { big (} (1-u) mathbf {a} _ {1} + u mathbf {a} _ {2} { big)} + v { big (} (1-u) mathbf {b} _ {1} + u mathbf {b} _ {2} { big)} }$,

который является гиперболическим параболоидом, который интерполирует 4 точки ${ displaystyle mathbf {a} _ {1}, ; mathbf {a} _ {2}, ; mathbf {b} _ {1}, ; mathbf {b} _ {2} }$ билинейно.^[1]

Очевидно, линейчатая поверхность - это двояковыпуклая поверхность, потому что любая точка лежит на двух линиях поверхности.

Для примера, показанного на диаграмме:

${ Displaystyle mathbf {a} _ {1} = (0,0,0) ^ {T}, ; mathbf {a} _ {2} = (1,0,0) ^ {T}, ; mathbf {b} _ {1} = (0,1,0) ^ {T}, ; mathbf {b} _ {2} = (1,1,1) ^ {T} }$.

Гиперболический параболоид имеет уравнение ${ displaystyle z = xy}$.

Лента Мебиуса

е) Лента Мебиуса:

Линейчатая поверхность

${ Displaystyle mathbf {x} (u, v) = mathbf {c} (u) + v ; mathbf {r} (u)}$

с

${ displaystyle mathbf {c} (u) = ( cos 2u, sin 2u, 0) ^ {T} }$ (кружок как директриса),

${ Displaystyle mathbf {r} (u) = ( соз и соз 2u, соз и грех 2u, грех и) ^ {T} , quad 0 leq u < pi ,}$

содержит ленту Мёбиуса.

На диаграмме показана лента Мёбиуса для ${ displaystyle -0,3 leq v leq 0,3}$.

Простой расчет показывает ${ displaystyle det ( mathbf { dot {c}} (0) ;, ; mathbf { dot {r}} (0) ;, ; mathbf {r} (0)) ; neq ; 0 }$ (см. следующий раздел). Следовательно, данная реализация ленты Мёбиуса есть не разворачивается. Но есть разворачивающиеся ленты Мёбиуса.^[2]

Касательные плоскости, развертываемые поверхности

Для нижеследующих соображений предполагается, что существует любая необходимая производная.

Для определения вектора нормали в точке требуется частные производные представительства ${ displaystyle quad mathbf {x} (u, v) = mathbf {c} (u) + v ; mathbf {r} (u)}$ :

${ displaystyle mathbf {x} _ {u} = mathbf { dot {c}} (u) + v ; mathbf { dot {r}} (u) }$ ,${ Displaystyle quad mathbf {x} _ {v} = ; mathbf {r} (u)}$

Следовательно, нормальный вектор

• ${ displaystyle mathbf {n} = mathbf {x} _ {u} times mathbf {x} _ {v} = mathbf { dot {c}} times mathbf {r} + v ( mathbf { dot {r}} times mathbf {r}) .}$

Потому что ${ Displaystyle mathbf {п} cdot mathbf {r} = 0}$ (Смешанное произведение с двумя равными векторами всегда равно 0!), Vector ${ Displaystyle mathbf {r} (и_ {0})}$ является касательным вектором в любой точке ${ Displaystyle mathbf {х} (и_ {0}, v)}$. Касательные плоскости вдоль этой линии все одинаковы, если ${ displaystyle mathbf { dot {r}} times mathbf {r}}$ кратно ${ displaystyle mathbf { dot {c}} times mathbf {r}}$ . Это возможно, только если три вектора ${ Displaystyle mathbf { точка {с}} ;, ; mathbf { точка {r}} ;, ; mathbf {r} }$ лежат в плоскости, т.е. линейно зависимы. Линейную зависимость трех векторов можно проверить с помощью определителя этих векторов:

• Касательные плоскости вдоль линии ${ displaystyle mathbf {x} (u_ {0}, v) = mathbf {c} (u_ {0}) + v ; mathbf {r} (u_ {0})}$ равны, если

${ displaystyle det ( mathbf { dot {c}} (u_ {0}) ;, ; mathbf { dot {r}} (u_ {0}) ;, ; mathbf {r } (u_ {0})) ; = ; 0 .}$

Важность этого определяющего условия показывает следующее утверждение:

• Линейчатая поверхность ${ displaystyle quad mathbf {x} (u, v) = mathbf {c} (u) + v ; mathbf {r} (u)}$ является развивающийся в плоскость, если для любой точки Кривизна Гаусса исчезает. Это именно тот случай, если

${ displaystyle det ( mathbf { dot {c}} ;, ; mathbf { dot {r}} ;, ; mathbf {r}) ; = ; 0 quad}$

в любой момент верно.^[3]

Образующие любой линейчатой ​​поверхности сливаются с одним семейством ее асимптотических прямых. Для складывающихся поверхностей они также составляют одно семейство линии кривизны. Можно показать, что любой развивающийся поверхность - это конус, цилиндр или поверхность, образованная всеми касательными к пространственной кривой.^[4]

Дальнейшие примеры

• Коноид
• Каталонская поверхность
• Раздвижные ролики (олоид, сферикон)

Применение и история складывающихся поверхностей

Развивающееся соединение двух эллипсов и его развитие

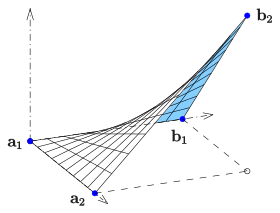
Детерминантное условие для развертывающихся поверхностей используется для определения численно складываемых связей между пространственными кривыми (директрисами). Схема показывает развивающуюся связь между двумя эллипсами, находящимися в разных плоскостях (одна горизонтальная, другая вертикальная), и ее развитие.^[5]

Впечатление от использования разворачивающихся поверхностей в Системы автоматизированного проектирования (CAD) дан в Интерактивный дизайн складывающихся поверхностей^[6]

А исторический обзор складывающихся поверхностей можно найти в Разрабатываемые поверхности: их история и применение^[7]

Линейчатые поверхности в алгебраической геометрии

В алгебраическая геометрия, линейчатые поверхности изначально были определены как проективные поверхности в проективное пространство содержащая прямую линию, проходящую через любую заданную точку. Это сразу означает, что есть проективная линия на поверхности, проходящая через любую заданную точку, и это условие теперь часто используется как определение линейчатой ​​поверхности: линейчатые поверхности определяются как абстрактные проективные поверхности, удовлетворяющие этому условию, что существует проективная линия. через любую точку. Это эквивалентно тому, что они бирациональный произведению кривой и проективной прямой. Иногда линейчатую поверхность определяют как поверхность, удовлетворяющую более сильному условию: расслоение над кривой, слои которой являются проективными прямыми. Это исключает проективную плоскость, которая имеет проективную прямую через каждую точку, но не может быть записана как такое расслоение.

Линейчатые поверхности появляются в Классификация Энрикес проективных комплексных поверхностей, потому что каждая алгебраическая поверхность Кодаира измерение ${ displaystyle - infty}$ - линейчатая поверхность (или проективная плоскость, если использовать ограничительное определение линейчатой ​​поверхности). Любая минимальная проективная линейчатая поверхность, отличная от проективной плоскости, является проективным расслоением 2-мерного векторного расслоения над некоторой кривой. Линейчатые поверхности с базовой кривой рода 0 являются Поверхности Хирцебруха.

Линейчатые поверхности в архитектуре

Поверхности с двойной линией - это вдохновение для изогнутых гиперболоидные структуры который может быть построен с решетка прямых элементов, а именно:

• Гиперболические параболоиды, такие как односкатные крыши.
• Гиперболоиды одного листа, например градирни и немного мусорные ведра.

В RM-81 Agena ракетный двигатель нанят прямо каналы охлаждения которые были выложены на линейчатой ​​поверхности, чтобы сформировать горло сопло раздел.

• 

  Охлаждение гиперболические башни в Электростанция Дидкот, ВЕЛИКОБРИТАНИЯ; поверхность может быть двоякой.

• 

  Дважды управляемая водонапорная башня с тороидальный танк, автор Ян Богуславский в Цеханув, Польша

• 

  Гиперболоид Башня порта Кобе, Кобе, Япония, с двойным решением.

• 

  Гиперболоидная водонапорная башня, 1896 г. Нижний Новгород.

• 

  В сетка из Шуховская башня в Москве, секции которой управляются двояко.

• 

  Винтовая лестница в линейку внутри Кремонас Торраццо.

• 

  Деревенская церковь в Село, Словения: и крыша (коническая), и стена (цилиндрическая) являются линейчатыми поверхностями.

• 

  А гиперболический параболоид крыша Железнодорожная станция Варшава-Охота в Варшава, Польша.

• 

  Управляемый коническая шляпа.

• 

  Гофрированная черепица, разделенная параллельными линиями в одном направлении, и синусоидальный в перпендикулярном направлении

• 

  Построение плоской поверхности линовкой (стяжка) конкретный

Рекомендации

• Ду Карму, Манфредо П.: Дифференциальная геометрия кривых и поверхностей., Прентис-Холл; 1 издание, 1976 г. ISBN 978-0132125895
• Barth, Wolf P .; Хулек, Клаус; Питерс, Крис А.М .; Ван де Вен, Антониус (2004), Компактные сложные поверхности, Ergebnisse der Mathematik и ихрер Гренцгебиете. 3. Folge., 4, Springer-Verlag, Берлин, Дои:10.1007/978-3-642-57739-0, ISBN 978-3-540-00832-3, МИСТЕР 2030225
• Бовиль, Арно (1996), Комплексные алгебраические поверхности, Студенческие тексты Лондонского математического общества, 34 (2-е изд.), Издательство Кембриджского университета, Дои:10.1017 / CBO9780511623936, ISBN 978-0-521-49510-3, МИСТЕР 1406314
• Эдж, В. Л. (1931), Теория линейчатых поверхностей, Cambridge University Press - через Интернет-архив. Рассмотрение: Бюллетень Американского математического общества 37 (1931), 791-793, Дои:10.1090 / S0002-9904-1931-05248-4
• Fuchs, D .; Табачников Серж (2007), «16.5 Нет неплоских трехлинейчатых поверхностей», Математический омнибус: тридцать лекций по классической математике, Американское математическое общество, стр. 228, ISBN 9780821843161.
• Ли, Ta-chʻien (ред.) (2011), Проблемы и решения математики, 3103 (2-е изд.), Всемирная научная издательская компанияCS1 maint: дополнительный текст: список авторов (связь).
• Гильберт, Дэвид; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN 978-0-8284-1087-8.
• Исковских, В.А. (2001) [1994], «Рифленая поверхность», Энциклопедия математики, EMS Press
• Шарп, Джон (2008), D-формы: удивительные новые трехмерные формы из плоских изогнутых форм, Тарквин, ISBN 978-1-899618-87-3. Обзор: Séquin, Карло Х. (2009), Журнал математики и искусств 3: 229–230, Дои:10.1080/17513470903332913

внешняя ссылка

• Вайсштейн, Эрик В. «Линейчатая поверхность». MathWorld.
• Изображения с линейчатой ​​поверхностью из Университета Аризоны
• Примеры развертываемых поверхностей на сайте Rhino3DE