WikiDer > Знак (математика)
Эта статья нужны дополнительные цитаты для проверка. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В математика, Концепция чего-либо знак происходит из того свойства, что каждый настоящий номер либо положительно, отрицательный или же нуль. В зависимости от местных соглашений ноль не считается ни положительным числом, ни отрицательным числом (не имеющим знака или собственного знака), либо принадлежащим как отрицательным, так и положительным числам (имеющим оба знака).[нужна цитата] Всякий раз, когда это специально не упомянуто, эта статья придерживается первой конвенции.
В некоторых случаях имеет смысл рассматривать подписанный ноль (Такие как представления с плавающей запятой действительных чисел в компьютерах). В математике и физике фраза «смена знака» связана с возникновением Противоположное число (отрицание или умножение на −1) любого объекта, который позволяет такое построение, и не ограничивается действительными числами. Он применяется среди других объектов к векторам, матрицам и комплексным числам,[1] которым не предписывается быть только положительным, отрицательным или нулевым. Слово «знак» также часто используется для обозначения других двоичных аспектов математических объектов, которые напоминают положительность и отрицательность, например нечетные и четные (знак перестановки), Чувство ориентация или вращение (ч / ч), односторонние ограничения, и другие концепции, описанные в § Прочие значения ниже.
Знак числа
Числа из различных систем счисления, например целые числа, рациональные, сложные числа, кватернионы, октонионы, ... может иметь несколько атрибутов, фиксирующих определенные свойства числа. Если система счисления имеет структуру заказанное кольцонапример, целые числа, он должен содержать число, которое не меняет ни одно число при добавлении к нему (добавка элемент идентичности). Это число обычно обозначается как 0. Из-за общий заказ в этом кольце есть числа больше нуля, называемые положительный числа. Для других свойств, требуемых внутри кольца, для каждого такого положительного числа существует число меньше, чем 0 которое при добавлении к положительному числу дает результат 0. Эти цифры меньше, чем 0 называются отрицательный числа. Цифры в каждой такой паре соответствуют им. аддитивное обратное. Этот атрибут числа, будучи исключительно либо нуль (0), положительный (+), или же отрицательный (−), называется его знак, и часто кодируется в действительные числа 0, 1, и −1, соответственно (аналогично тому, как функция знака определено).[2] Поскольку рациональные и действительные числа также являются упорядоченными кольцами (даже поля), эти системы счисления имеют одинаковые знак атрибут.
Пока в арифметика, знак минус обычно считается представлением бинарной операции вычитания в алгебра, обычно считается, что унарная операция уступая Противоположное число (иногда называют отрицание) операнда. Пока 0 является собственной аддитивной инверсией (−0 = 0), аддитивное обратное положительное число отрицательно, а аддитивное обратное отрицательное число положительно. Двойное применение этой операции записывается как −(−3) = 3. Знак плюс в основном используется в алгебре для обозначения бинарной операции сложения и лишь изредка для того, чтобы подчеркнуть положительность выражения.
В общем цифровое обозначение (используется в арифметика и в других местах), знак числа часто делается явным, помещая знак плюс или минус перед числом. Например, +3 обозначает «положительную тройку», и −3 обозначает «отрицательную тройку» (алгебраически: аддитивная инверсия 3). Без определенного контекста (или когда не указан явный знак) число по умолчанию интерпретируется как положительное. Эта запись устанавливает сильную ассоциацию знака минус "−"с отрицательными числами, и знак плюс" + "с положительными числами.
Знак нуля
В рамках соглашения нуль не будучи ни положительным, ни отрицательным, конкретное знаковое значение 0 может быть присвоено числовое значение 0. Это эксплуатируется в -функция, как определено для действительных чисел.[2] В арифметике +0 и −0 оба обозначают одно и то же число 0. Обычно нет опасности спутать значение с его знаком, хотя соглашение о присвоении обоих знаков 0 не сразу допускает эту дискриминацию.
В некоторых контекстах, особенно в вычисление, полезно рассматривать подписанные версии нуля, с подписанные нули ссылаясь на различные представления дискретных чисел (см. представление числа со знаком для большего).
Символы +0 и −0 редко появляются в качестве замены 0+ и 0−, используется в исчисление и математический анализ за односторонние ограничения (правый предел и левый предел соответственно).[3] Это обозначение относится к поведению функции при приближении ее реальной входной переменной. 0 по положительным (соответственно отрицательным) значениям; эти два ограничения могут не существовать или согласовываться.
Терминология знаков
Когда 0 не считается ни положительным, ни отрицательным, следующие фразы могут относиться к знаку числа:
- Число положительный если он больше нуля.
- Число отрицательный если он меньше нуля.
- Число неотрицательный если он больше или равен нулю.
- Число неположительный если он меньше или равен нулю.
Когда 0 считается как положительным, так и отрицательным, измененные фразы используются для обозначения знака числа:
- Число строго положительный если он больше нуля.
- Число строго отрицательный если он меньше нуля.
- Число положительный если он больше или равен нулю.
- Число отрицательный если он меньше или равен нулю.
Например, абсолютная величина действительного числа всегда «неотрицательно», но не обязательно «положительно» в первой интерпретации, тогда как во второй интерпретации оно называется «положительным», хотя и не обязательно «строго положительным».
Та же терминология иногда используется для функции которые дают действительные или другие значения со знаком. Например, функция будет называться положительная функция если его значения положительны для всех аргументов его домена, или неотрицательная функция если все его значения неотрицательны.
Сложные числа
Комплексные числа невозможно упорядочить, поэтому они не могут нести структуру упорядоченного кольца и, соответственно, не могут быть разделены на положительные и отрицательные комплексные числа. Однако у них есть общий атрибут с вещественными числами, который называется абсолютная величина или же величина. Величины всегда являются неотрицательными действительными числами, и любому ненулевому числу принадлежит положительное действительное число, его абсолютная величина.
Например, абсолютное значение −3 и абсолютное значение 3 оба равны 3. Это записывается символами как |−3| = 3 и |3| = 3.
В общем, любое произвольное действительное значение можно определить по его величине и знаку. Используя стандартное кодирование, любое действительное значение дается произведением величины и знака в стандартном кодировании. Это соотношение можно обобщить, чтобы определить знак для комплексных чисел.
Поскольку действительные и комплексные числа образуют поле и содержат положительные действительные числа, они также содержат обратные величины всех ненулевых чисел. Это означает, что любое ненулевое число можно умножить на величину, обратную его величине, то есть разделить на его величину. Непосредственно частное любого ненулевого действительного числа по его величине дает в точности его знак. По аналогии знак комплексного числа z можно определить как частное из z и это величина |z|. Поскольку величина комплексного числа равна разделен, получившийся знак комплексного числа в некотором смысле представляет его сложный аргумент. Это нужно сравнивать со знаком действительных чисел, за исключением Для определения сложной знак-функции. видеть § Комплексная знаковая функция ниже.
Знаковые функции
При работе с числами часто бывает удобно иметь их знак в виде числа. Это достигается функциями, которые извлекают знак любого числа и сопоставляют его с предопределенным значением, прежде чем сделать его доступным для дальнейших вычислений. Например, было бы полезно сформулировать сложный алгоритм только для положительных значений и позаботиться о знаке только после этого.
Функция вещественного знака
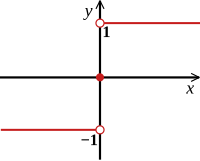
В функция знака или же сигнум функция извлекает знак действительного числа, сопоставляя набор действительных чисел с набором из трех действительных чисел Его можно определить так:[2]
Таким образом sgn (Икс) равно 1, когда Икс положительный, и sgn (Икс) равно -1, когда Икс отрицательный. Для ненулевых значений Икс, эту функцию также можно определить по формуле
- ,
куда |Икс| это абсолютная величина из Икс.
Комплексная знаковая функция
В то время как действительное число имеет одномерное направление, комплексное число имеет двумерное направление. Для сложной знаковой функции требуется величина своего аргумента z = Икс + иу, который можно рассчитать как
Аналогично предыдущему, сложная знаковая функция извлекает комплексный знак комплексного числа, отображая набор ненулевых комплексных чисел в набор унимодулярных комплексных чисел, и 0 к 0: Его можно определить следующим образом:
Позволять z быть также выраженным его величиной и одним из его аргументов φ в качестве z = |z|⋅еiφ, тогда[4]
Это определение также может быть распознано как нормализованный вектор, то есть вектор, направление которого не меняется, а длина фиксирована на единство. Если исходное значение было R, θ в полярной форме, то sign (R, θ) равно 1 θ. Расширение sign () или signum () до любого количества измерений очевидно, но это уже было определено как нормализация вектора.
Знаков по соглашению
В ситуациях, когда существует ровно две равноправные возможности для атрибута, они часто по соглашению обозначаются как плюс и минус, соответственно. В некоторых контекстах выбор этого присвоения (то есть, какой диапазон значений считается положительным, а какой отрицательным) является естественным, тогда как в других контекстах выбор является произвольным, что делает необходимым явное соглашение о знаках, единственное требование - последовательное использование конвенция.
Знак угла

Во многих контекстах принято связывать знак с мерой угол, особенно ориентированный угол или угол вращение. В такой ситуации знак указывает, находится ли угол в по часовой стрелке или против часовой стрелки. Хотя могут использоваться разные условные обозначения, в математика чтобы углы против часовой стрелки считались положительными, а углы по часовой стрелке считались отрицательными.[5]
Также можно связать знак с углом поворота в трех измерениях, предполагая, что ось вращения был ориентирован. В частности, правша вращение вокруг ориентированной оси обычно считается положительным, в то время как левое вращение считается отрицательным.
Признак изменения
Когда количество Икс меняется со временем, изменять в стоимости Икс обычно определяется уравнением
Используя это соглашение, увеличение Икс считается положительным изменением, а уменьшение Икс считается отрицательным изменением. В исчисление, это же соглашение используется в определении производная. В результате любые возрастающая функция имеет положительную производную, в то время как любая убывающая функция имеет отрицательную производную.
Знак направления
В аналитическая геометрия и физика, некоторые направления принято обозначать как положительные или отрицательные. В качестве базового примера числовая строка обычно рисуется с положительными числами справа и отрицательными числами слева:
В результате при обсуждении линейное движение, смещение или же скорость, движение вправо обычно считается положительным, в то время как аналогичное движение влево считается отрицательным.
На Декартова плоскость, правое и восходящее направления обычно считаются положительными, а правое - положительным. Икс-направление, а вверх - положительное у-направление. Если смещение или скорость вектор разделен на компоненты вектора, тогда горизонтальная часть будет положительной для движения вправо и отрицательной для движения влево, а вертикальная часть будет положительной для движения вверх и отрицательной для движения вниз.
Подпись в вычислениях
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Большинство компьютеров используют два дополнения для представления знака целого числа. | |||||||||
В вычисление, целочисленное значение может быть со знаком или без знака, в зависимости от того, отслеживает ли компьютер знак для числа. Ограничивая целое число Переменная только на неотрицательные значения, еще одно кусочек может использоваться для хранения значения числа. Поскольку целочисленные арифметические операции выполняются на компьютерах, представление числа со знаком обычно не хранят знак как отдельный независимый бит, вместо этого используя, например, два дополнения.
Напротив, действительные числа хранятся и обрабатываются как плавающая точка значения. Значения с плавающей запятой представлены тремя отдельными значениями: мантиссой, показателем степени и знаком. Имея этот отдельный знаковый бит, можно представлять как положительный, так и отрицательный ноль. Большинство языков программирования обычно рассматривают положительный ноль и отрицательный ноль как эквивалентные значения, хотя они предоставляют средства, с помощью которых можно обнаружить различие.
Другие значения
Помимо знака действительного числа, слово «знак» также используется по-разному в математике и других науках:
- Слова вплоть до знак означает, что для количества q, известно, что либо q = Q или же q = −Q для некоторых Q. Часто это выражается как q = ±Q. Для действительных чисел это означает, что только абсолютная величина |q| количество известно. За сложные числа и векторов, величина, известная до знака, является более сильным условием, чем величина с известными величина: в стороне Q и −Q, есть много других возможных значений q такой, что |q| = |Q|.
- В знак перестановки определяется как положительное, если перестановка четное, и отрицательное, если перестановка нечетное.
- В теория графов, а подписанный граф - это граф, в котором каждое ребро помечено положительным или отрицательным знаком.
- В математический анализ, а подписанная мера является обобщением концепции мера в котором мера набора может иметь положительные или отрицательные значения.
- В представление цифр со знаком, каждая цифра числа может иметь положительный или отрицательный знак.
- Идеи подписанная область и подписанный том иногда используются, когда определенные области или объемы удобно считать отрицательными. Это особенно верно в теории детерминанты. В (аннотации) ориентированное векторное пространствокаждый упорядоченный базис векторного пространства можно классифицировать как положительно или отрицательно ориентированный.
- В физика, любой электрический заряд идет со знаком, положительным или отрицательным. По соглашению, положительный заряд - это заряд того же знака, что и у протон, а отрицательный заряд - это заряд того же знака, что и у электрон.
Смотрите также
Рекомендации
- ^ «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-26.
- ^ а б c Вайсштейн, Эрик В. "Знак". mathworld.wolfram.com. Получено 2020-08-26.
- ^ «Список математических и аналитических символов». Математическое хранилище. 2020-05-11. Получено 2020-08-26.
- ^ «СигнумФункция». www.cs.cas.cz. Получено 2020-08-26.
- ^ «Знак углов | Что такое угол? | Положительный угол | Отрицательный угол». Математика только математика. Получено 2020-08-26.