WikiDer > Сингулярная функция

Singular function
О шотландской горной тропе на Гленко см. Аонах Игах.
График числа намотки круговая карта является примером сингулярной функции.

В математика, а функция с действительным знаком ж на интервал [а, б] называется единственное число если он имеет следующие свойства:

  • ж является непрерывный на [а, б]. (**)
  • существует набор N из мера 0 такой, что для всех Икс вне N то производная ж ′(Икс) существует и равна нулю, то есть производная от ж исчезает почти всюду.
  • ж непостоянна на [а, б].

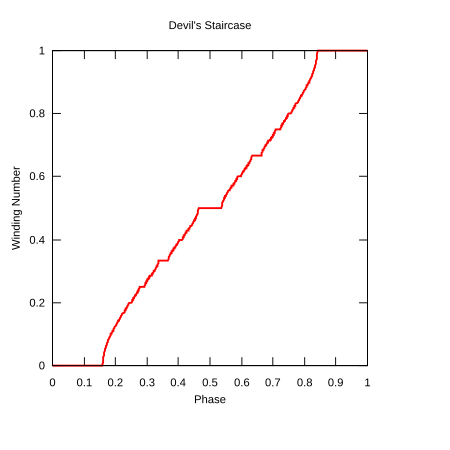
Стандартный пример сингулярной функции - это Функция Кантора, который иногда называют лестницей дьявола (термин также используется для сингулярных функций в целом). Однако есть и другие функции, получившие это имя. Один определяется с точки зрения круговая карта.

Если ж(Икс) = 0 для всех Икс ≤ а и ж(Икс) = 1 для всех Икс ≥ б, то функцию можно представить как кумулятивная функция распределения для случайная переменная что не является ни дискретная случайная величина (поскольку вероятность равен нулю для каждой точки), ни абсолютно непрерывная случайная величина (поскольку плотность вероятности равен нулю везде, где он существует).

Сингулярные функции возникают, например, как последовательности пространственно модулированных фаз или структур в твердые вещества и магниты, описанный в прототипе Модель Френкеля – Конторовой. и по Модель ANNNI, а также в некоторых динамические системы. Пожалуй, самое известное то, что они лежат в центре дробный квантовый эффект Холла.

При обращении к функциям с особенностью

При обсуждении математический анализ в целом или более конкретно реальный анализ или комплексный анализ или дифференциальные уравнения, это обычное явление для функции, содержащей математическая особенность называться «сингулярной функцией». Это особенно верно при обращении к функциям, которые расходятся до бесконечности в точке или на границе. Например, можно сказать: "1 / х становится сингулярным в начале координат, поэтому 1 / х является сингулярной функцией ".

Продвинутые методы работы с функциями, содержащими особенности, разработаны в теме под названием распределительный или обобщенная функция анализ. А слабая производная определено, что позволяет использовать сингулярные функции в уравнения в частных производных, так далее.

Смотрите также

использованная литература

(**) Это условие зависит от использованная литература[1]

  1. ^ сингулярная функция - Интернет-справочник Springer