WikiDer > Последовательность Спекера

Последовательность Спекера. В п^th цифра x_k является 4 если п ≤ k и вычисление {п}(п) останавливается после k шаги; в противном случае это 3.

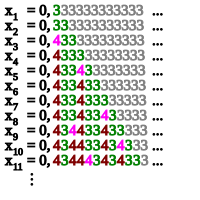
В теория вычислимости, а Последовательность Спекера это вычислимый, монотонно возрастающий, ограниченный последовательность из рациональное число чья супремум это не вычислимое действительное число. Первый пример такой последовательности был построен Эрнст Шпекер (1949).

Существование последовательностей Шпекера имеет последствия для вычислимый анализ. Тот факт, что такие последовательности существуют, означает, что набор всех вычислимых действительных чисел не удовлетворяет принцип наименьшей верхней границы реального анализа, даже если рассматривать только вычислимые последовательности. Обычный способ решить эту проблему - рассматривать только последовательности, сопровождаемые модуль сходимости; никакая последовательность Шпекера не имеет вычислимого модуля сходимости. В более общем смысле последовательность Спекера называется рекурсивный контрпример принципу наименьшей верхней границы, то есть конструкции, которая показывает, что эта теорема неверна при ограничении вычислимыми действительными числами.

Принцип наименьшей верхней границы также был проанализирован в программе обратная математика, где была определена точная сила этого принципа. В терминологии этой программы принцип наименьшей верхней границы эквивалентен ACA₀ через RCA₀. Фактически, доказательство прямой импликации, то есть того, что принцип наименьшей верхней границы влечет ACA₀, легко получается из хрестоматийного доказательства (см. Simpson, 1999) невычислимости супремума в принципе точной верхней границы.

строительство

Следующая конструкция описана Кушнером (1984). Позволять А быть любым рекурсивно перечислимый набор из натуральные числа это не разрешимый, и разреши (а_я) - вычислимое перечисление А без повторения. Определите последовательность (q_п) рациональных чисел с правилом

${displaystyle q_ {n} = sum _ {i = 0} ^ {n} 2 ^ {- a_ {i} -1}.}$

Понятно, что каждый q_п неотрицательна и рациональна, и что последовательность q_п строго увеличивается. Более того, поскольку а_я не имеет повторов, можно оценить каждый q_п против серии

${displaystyle sum _ {i = 0} ^ {infty} 2 ^ {- i-1} = 1.}$

Таким образом, последовательность (q_п) ограничено сверху числом 1. Классически это означает, что q_п имеет супремум Икс.

Показано, что Икс не является вычислимым действительным числом. Доказательство использует конкретный факт о вычислимых действительных числах. Если Икс были вычислимы, тогда было бы вычислимая функция р(п) такой, что |q_j - q_я| < 1/п для всех я,j > р(п). Вычислить рсравните двоичное разложение Икс с двоичным разложением q_я для все больших и больших значений я. Определение q_я заставляет единственную двоичную цифру каждый раз переходить от 0 до 1 я увеличивается на 1. Таким образом, будет несколько п где достаточно большой начальный сегмент Икс уже определено q_п что никакие дополнительные двоичные цифры в этом сегменте не могут быть включены, что приводит к оценке расстояния между q_я и q_j для я,j > п.

Если есть такая функция р были вычислимы, это привело бы к процедуре принятия решения для А, следующим образом. Учитывая ввод k, вычислить р(2^k+1). Если k должны были появиться в последовательности (а_я), это вызовет последовательность (q_я) увеличить на 2^−k-1, но этого не может произойти, если все элементы (q_я) находятся в пределах 2^−k-1 друг друга. Таким образом, если k будет перечислен в а_я, он должен быть пронумерован для значения я меньше, чем р(2^k+1). Это оставляет конечное число возможных мест, где k можно перечислить. Чтобы завершить процедуру принятия решения, проверьте их эффективным образом и верните 0 или 1 в зависимости от того, k найден.

Смотрите также

• Расчет в пределе

использованная литература

• Дуглас Бриджес и Фред Ричман. Разновидности конструктивной математики, Оксфорд, 1987.
• Б.А. Кушнер (1984), Лекции по конструктивному математическому анализу, Американское математическое общество, Переводы математических монографий т. 60.
• Якоб Г. Симонсен (2005), «Повторное посещение последовательностей Шпекера», Mathematical Logic Quarterly, v. 51, pp. 532–540. Дои:10.1002 / malq.200410048
• С. Симпсон (1999), Подсистемы арифметики второго порядка, Springer.
• Э. Спекер (1949), "Nicht konstruktiv beweisbare Sätze der Analysis" Журнал символической логики, т. 14, с. 145–158.