WikiDer > Т-норма

В математика, а t-норма (также Т-норма или, без сокращений, треугольная норма) является своего рода бинарная операция используется в рамках вероятностные метрические пространства И в многозначная логикаособенно в нечеткая логика. T-норма обобщает пересечение в решетка и соединение в логика. Название треугольная норма относится к тому факту, что в рамках вероятностных метрических пространств t-нормы используются для обобщения неравенство треугольника обычных метрические пространства.

Определение

T-норма - это функция T: [0, 1] × [0, 1] → [0, 1], который удовлетворяет следующим свойствам:

• Коммутативность: T (а, б) = Т (б, а)
• Монотонность: T (а, б) ≤ T (c, d) если а ≤ c и б ≤ d
• Ассоциативность: T (а, Т (б, c)) = T (T (а, б), c)
• Число 1 действует как элемент идентичности: T (а, 1) = а

Поскольку t-норма - это бинарная алгебраическая операция на интервале [0, 1] также распространены инфиксные алгебраические обозначения, при этом t-норма обычно обозначается через${ displaystyle *}$.

Определяющие условия t-нормы в точности соответствуют условиям частично упорядоченного абелева моноида на вещественном единичном интервале [0, 1]. (См.упорядоченная группа.) Моноидальная операция любого частично упорядоченного абелева моноида L поэтому некоторые авторы называют треугольная норма на L.

Мотивы и приложения

T-нормы являются обобщением обычных двузначных логическое соединение, изучаемых классической логикой, для нечеткая логика. Действительно, классическая булева конъюнкция коммутативна и ассоциативна. Свойство монотонности гарантирует, что степень правды соединения не уменьшается, если ценности истины союзов увеличиваются. Требование, чтобы 1 был тождественным элементом, соответствует интерпретации 1 как истинный (и, следовательно, 0 при ложный). Непрерывность, которая часто требуется и от нечеткого соединения, выражает идею о том, что, грубо говоря, очень небольшие изменения истинностных значений конъюнктов не должны макроскопически влиять на истинностное значение их соединения.

T-нормы также используются для построения пересечение из нечеткие множества или в качестве основы для операторов агрегирования (см. операции с нечеткими множествами). В вероятностные метрические пространства, t-нормы используются для обобщения неравенство треугольника обычных метрических пространств. Индивидуальные t-нормы, конечно, могут часто встречаться в дальнейших дисциплинах математики, так как класс содержит много знакомых функций.

Классификация t-норм

T-норма называется непрерывный если это непрерывный как функция, в обычной интервальной топологии на [0, 1]². (Аналогично для оставили- и право-непрерывность.)

T-норма называется строгий если он непрерывен и строго монотонный.

T-норма называется нильпотентный если он непрерывен и каждый Икс в открытом интервале (0, 1) его нильпотентный элемент, т.е. есть натуральное число п такой, что Икс ${ displaystyle *}$ ... ${ displaystyle *}$ Икс (п раз) равно 0.

T-норма ${ displaystyle *}$ называется Архимедов если у него есть Архимедова собственность, т.е. если для каждого Икс, у в открытом интервале (0, 1) есть натуральное число п такой, что Икс ${ displaystyle *}$ ... ${ displaystyle *}$ Икс (п раз) меньше или равно у.

Обычное частичное упорядочение t-норм поточечное, т. Е.

Т₁ ≤ т₂ Если T₁(а, б) ≤ T₂(а, б) для всех а, б в [0, 1].

Как функции, поточечные большие t-нормы иногда называют сильнее чем те точечно меньшие. Однако в семантике нечеткой логики чем больше t-норма, тем слабее (с точки зрения логической силы) соединение, которое оно представляет.

Выдающиеся примеры

График минимальной t-нормы (3D и контуры)

• Минимальная t-норма ${ displaystyle top _ { mathrm {min}} (a, b) = min {a, b },}$ также называется Т-норма Гёделя, поскольку это стандартная семантика для конъюнкции в Нечеткая логика Гёделя. Кроме того, он встречается в большинстве нечетких логик, основанных на t-норме, как стандартная семантика для слабой конъюнкции. Это поточечная наибольшая t-норма (см. свойства t-норм ниже).

График t-нормы продукта

• T-норма продукта ${ displaystyle top _ { mathrm {prod}} (a, b) = a cdot b}$ (обычное произведение действительных чисел). Помимо других применений, t-норма продукта является стандартной семантикой для сильной конъюнкции в нечеткая логика продукта. Это строгая архимедова t-норма.

График t-нормы Лукасевича

• Лукасевич t-норма ${ displaystyle top _ { mathrm {Luk}} (a, b) = max {0, a + b-1 }.}$ Название происходит от того факта, что t-норма является стандартной семантикой для сильной конъюнкции в Нечеткая логика Лукасевича. Это нильпотентная архимедова t-норма, поточечно меньшая, чем t-норма произведения.

График резкой t-нормы. Функция разрывна на линиях 0 < Икс = 1 и 0 < у = 1.

• Резкая t-норма

${ displaystyle top _ { mathrm {D}} (a, b) = { begin {cases} b & { mbox {if}} a = 1 a & { mbox {if}} b = 1 0 & { mbox {в противном случае.}} End {case}}}$

Название отражает тот факт, что экстремальная t-норма - это поточечно наименьшая t-норма (см. свойства t-норм ниже). Это непрерывная справа архимедова t-норма.

График нильпотентного минимума. Функция разрывная на прямой 0 < Икс = 1 − у < 1.

• Нильпотентный минимум

${ displaystyle top _ { mathrm {nM}} (a, b) = { begin {cases} min (a, b) & { mbox {if}} a + b> 1 0 & { mbox {иначе}} end {case}}}$

является стандартным примером t-нормы, которая непрерывна слева, но не непрерывна. Несмотря на свое название, нильпотентный минимум не является нильпотентной t-нормой.

График продукта Hamacher

• Продукция Hamacher

${ displaystyle top _ { mathrm {H} _ {0}} (a, b) = { begin {cases} 0 & { mbox {if}} a = b = 0 { frac {ab} {a + b-ab}} & { mbox {иначе}} end {case}}}$

является строгой архимедовой t-нормой и важным представителем параметрических классов Т-нормы Hamacher и T-нормы Швейцера – Склара.

Свойства t-норм

Резкая t-норма - это поточечная наименьшая t-норма, а минимальная - поточечная наибольшая t-норма:

${ displaystyle top _ { mathrm {D}} (a, b) leq top (a, b) leq mathrm { top _ {min}} (a, b),}$ для любой t-нормы ${ displaystyle top}$ и все а, б в [0, 1].

Для каждой t-нормы T число 0 действует как нулевой элемент: T (а, 0) = 0 для всех а в [0, 1].

T-норма T имеет делители нуля если и только если у него есть нильпотентный элементы; каждый нильпотентный элемент T также является делителем нуля T. Множество всех нильпотентных элементов представляет собой интервал [0,а] или [0,а), для некоторых а в [0, 1].

Свойства непрерывных t-норм

Хотя действительные функции двух переменных могут быть непрерывными по каждой переменной, но не по [0, 1]², это не относится к t-нормам: t-норма T непрерывна тогда и только тогда, когда она непрерывна по одной переменной, т. е. тогда и только тогда, когда функции ж_у(Икс) = Т (Икс, у) непрерывны для каждого у в [0, 1]. Аналогичные теоремы верны для непрерывности t-нормы слева и справа.

Непрерывная t-норма архимедова тогда и только тогда, когда 0 и 1 являются ее единственными идемпотенты.

Непрерывная архимедова t-норма является строгой, если 0 является ее единственным нильпотентный элемент; в противном случае он нильпотентен. Более того, по определению непрерывная архимедова t-норма T нильпотентна тогда и только тогда, когда каждый Икс <1 является нильпотентным элементом T. Таким образом, с непрерывной архимедовой t-нормой T либо все, либо ни один из элементов (0, 1) нильпотентны. Если все элементы в (0, 1) нильпотентны, то t-норма изоморфна t-норме Лукасевича; т.е. существует строго возрастающая функция ж такой, что

${ displaystyle top (x, y) = f ^ {- 1} ( top _ { mathrm {Luk}} (f (x), f (y))).}$

С другой стороны, если в T нет нильпотентных элементов, t-норма изоморфна t-норме произведения. Другими словами, все нильпотентные t-нормы изоморфны, t-норма Лукасевича является их прототипическим представителем; и все строгие t-нормы изоморфны, а t-норма произведения является их прототипом. T-норма Лукасевича сама изоморфна t-норме произведения с подрезкой в ​​0,25, т. Е. Функции п(Икс, у) = макс (0,25, Икс · у) на [0.25, 1]².

Для каждой непрерывной t-нормы множество ее идемпотентов является замкнутым подмножеством [0, 1]. Его дополнение - множество всех элементов, которые не являются идемпотентными, - поэтому объединение счетного числа неперекрывающихся открытых интервалов. Ограничение t-нормы на любой из этих интервалов (включая его конечные точки) архимедово и, следовательно, изоморфно t-норме Лукасевича или t-норме произведения. Для таких Икс, у которые не попадают в тот же открытый интервал неидемпотентов, t-норма оценивается как минимум Икс и у. Эти условия фактически дают характеристику непрерывных t-норм, называемых Теорема Мостерта – Шилдса, так как таким образом может быть разложена всякая непрерывная t-норма, и описанная конструкция всегда дает непрерывную t-норму. Теорема также может быть сформулирована следующим образом:

T-норма непрерывна тогда и только тогда, когда она изоморфна порядковая сумма минимума, Лукасевича и t-нормы произведения.

Аналогичная характеризационная теорема для прерывных t-норм неизвестна (даже для непрерывных слева), только некоторые неисчерпывающие методы для построение t-норм были найдены.

Остаток

Для любой непрерывной слева t-нормы ${ displaystyle top}$, есть уникальная бинарная операция ${ displaystyle Rightarrow}$ на [0, 1] такие, что

${ Displaystyle верх (г, х) leq у}$ если и только если ${ Displaystyle г Leq (х Rightarrow у)}$

для всех Икс, у, z в [0, 1]. Эта операция называется остаток t-нормы. В префиксной записи остаток до t-нормы ${ displaystyle top}$ часто обозначается как ${ displaystyle { vec { top}}}$ или буквой Р.

Интервал [0, 1], снабженный t-нормой и его остатком, образует остаточная решетка. Отношение между t-нормой T и ее остатком R является примером примыкание (в частности, Связь Галуа): остаток образует правый сопряженный R (Икс, -) к функтору T (-, Икс) для каждого Икс в решетке [0, 1], взятой в качестве категория poset.

В стандартной семантике нечетких логик, основанных на t-норме, где конъюнкция интерпретируется t-нормой, остаток играет роль импликации (часто называемой R-импликация).

Основные свойства остатка

Если ${ displaystyle Rightarrow}$ является вычетом непрерывной слева t-нормы ${ displaystyle top}$, тогда

${ displaystyle (x Rightarrow y) = sup {z mid top (z, x) leq y }.}$

Следовательно, для всех Икс, у в единичном интервале,

${ Displaystyle (х Rightarrow y) = 1}$ если и только если ${ displaystyle x leq y}$

и

${ displaystyle (1 Rightarrow y) = y.}$

Если ${ displaystyle *}$ является непрерывной слева t-нормой и ${ displaystyle Rightarrow}$ его остаток, то

${ displaystyle { begin {array} {rcl} min (x, y) & geq & x * (x Rightarrow y) max (x, y) & = & min ((x Rightarrow y) ) Rightarrow y, (y Rightarrow x) Rightarrow x). End {array}}}$

Если ${ displaystyle *}$ непрерывно, то в первом равенство выполняется.

Вычетов выдающихся непрерывных слева t-норм

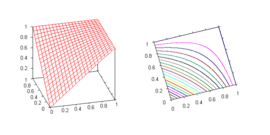
Если Икс ≤ у, то R (Икс, у) = 1 для любого остатка R. Поэтому в следующей таблице приведены значения выдающегося остатка только для Икс > у.

Остаток	Имя	Значение для Икс > у	График
Минимальная t-норма	Стандартная импликация Гёделя	у	Стандартная импликация Гёделя. Функция разрывная на линии у = Икс < 1.
T-норма продукта	Гогуэн значение	у / Икс	Смысл Гогена. Функция разрывна в точке Икс = у = 0.
Лукасевич t-норма	Стандартная импликация Лукасевича	1 – Икс + у	Стандартная импликация Лукасевича.
Нильпотентный минимум		макс (1 - Икс, у)	Остаток нильпотентного минимума. Функция разрывная на прямой 0 < у = Икс < 1.

Т-конормы

Т-конормы (также называемый S-нормы) двойственны t-нормам при операции изменения порядка, которая присваивает 1 - Икс к Икс на [0, 1]. Учитывая t-норму ${ displaystyle top}$, дополнительная конорма определяется формулой

${ displaystyle bot (a, b) = 1- top (1-a, 1-b).}$

Это обобщает Законы де Моргана.

Отсюда следует, что t-конорма удовлетворяет следующим условиям, которые можно использовать для эквивалентного аксиоматического определения t-конорм независимо от t-норм:

• Коммутативность: ⊥ (а, б) = ⊥(б, а)
• Монотонность: ⊥ (а, б) ≤ ⊥(c, d) если а ≤ c и б ≤ d
• Ассоциативность: ⊥ (а, ⊥(б, c)) = ⊥(⊥(а, б), c)
• Элемент идентичности: ⊥ (а, 0) = а

Т-конормы используются для представления логическая дизъюнкция в нечеткая логика и союз в теория нечетких множеств.

Примеры т-конорм

Важными t-конормами являются те, которые двойственны известным t-нормам:

График максимальной t-конормы (3D и контуры)

• Максимальный t-конорм ${ displaystyle bot _ { mathrm {max}} (a, b) = max {a, b }}$, двойственная минимальной t-норме, является наименьшей t-конормой (см. свойства т-конорм ниже). Это стандартная семантика дизъюнкции в Нечеткая логика Гёделя и для слабой дизъюнкции во всех нечетких логиках, основанных на t-норме.

График вероятностной суммы

• Вероятностная сумма ${ displaystyle bot _ { mathrm {sum}} (a, b) = a + b-a cdot b = 1- (1-a) cdot (1-b)}$ двойственна t-норме произведения. В теория вероятности он выражает вероятность объединения независимых События. Это также стандартная семантика для сильной дизъюнкции в таких расширениях нечеткая логика продукта в которых она определима (например, содержащие инволютивное отрицание).

График t-конормы ограниченной суммы

• Ограниченная сумма ${ displaystyle bot _ { mathrm {Luk}} (a, b) = min {a + b, 1 }}$ двойственна t-норме Лукасевича. Это стандартная семантика сильной дизъюнкции в Нечеткая логика Лукасевича.

График резкого т-конорма. На линиях 1> функция разрывная. Икс = 0 и 1> у = 0.

• Резкий т-конорм

${ displaystyle bot _ { mathrm {D}} (a, b) = { begin {cases} b & { mbox {if}} a = 0 a & { mbox {if}} b = 0 1 & { mbox {в противном случае}} end {case}}}$

двойственная к радикальной t-норме, является наибольшей t-конормой (см. свойства т-конорм ниже).

График нильпотентного максимума. Функция разрывная на прямой 0 < Икс = 1 – у < 1.

• Нильпотентный максимум, двойственный нильпотентному минимуму:

${ displaystyle bot _ { mathrm {nM}} (a, b) = { begin {cases} max (a, b) & { mbox {if}} a + b <1 1 & { mbox {иначе.}} end {case}}}$

График суммы Эйнштейна

• Сумма Эйнштейна (сравните формула сложения скоростей по специальной теории относительности)

${ displaystyle bot _ { mathrm {H} _ {2}} (a, b) = { frac {a + b} {1 + ab}}}$

является двойником к одному из Т-нормы Hamacher.

Свойства т-конорм

Многие свойства t-конорм могут быть получены путем дуализации свойств t-норм, например:

• Для любой t-конормы ⊥ число 1 является аннулирующим элементом: ⊥ (а, 1) = 1, для любого а в [0, 1].
• По отношению к t-нормам все t-конормы ограничены максимумом и сильной t-конормой:

${ displaystyle mathrm { bot _ {max}} (a, b) leq bot (a, b) leq bot _ { mathrm {D}} (a, b)}$, для любого т-конорма ${ displaystyle bot}$ и все а, б в [0, 1].

Дальнейшие свойства являются результатом отношений между t-нормами и t-конормами или их взаимодействием с другими операторами, например:

• T-норма T распределяет над t-конормой ⊥, т. е.

Т (Икс, ⊥(у, z)) = ⊥ (T (Икс, у), Т (Икс, z)) для всех Икс, у, z в [0, 1],

тогда и только тогда, когда ⊥ - максимальная t-конорма. Соответственно, любая t-конорма распределяется по минимуму, но не по любой другой t-норме.

Нестандартные отрицатели

А отрицатель ${ displaystyle n: [0,1] по [0,1]}$ это однообразный падение, я. е. отображение обратного порядка с ${ Displaystyle п (0) = 1}$ и ${ Displaystyle п (1) = 0}$ (в других обозначениях: ${ displaystyle 0 mapsto 1}$ и ${ displaystyle 1 mapsto 0}$). Негатор n называется

• строгий в случае строгой монотонности
• сильный если он строгий и инволютивный (см .: инволюция): ${ displaystyle forall}$ ${ Displaystyle х в [0,1]: п (п (х)) = х}$.

Стандартный (канонический) отрицатель - это ${ Displaystyle п (х) = 1-х, х в [0,1]}$, который одновременно строг и силен. Поскольку в приведенном выше определении пары t-норма / t-конорма используется стандартный отрицатель, его можно обобщить следующим образом:

А Де Морган Триплет является тройкой (T, ⊥, n) если только (если и только если)

1. T - t-норма
2. ⊥ является t-конормой в соответствии с аксиоматическим определением t-конорм, упомянутым выше.
3. n - сильный отрицатель
4. ${ displaystyle forall a, b in [0,1]: , n ( perp (a, b)) = top (n (a), n (b))}$.

^[1]

Смотрите также

• Построение t-норм
• Нечеткие логики T-нормы

Рекомендации

• Клемент, Эрих Петер; Месияр, Радько; и Пап, Эндре (2000), Треугольные нормы. Дордрехт: Клувер. ISBN 0-7923-6416-3.
• Гайек, Петр (1998), Метаматематика нечеткой логики. Дордрехт: Клувер. ISBN 0-7923-5238-6
• Cignoli, Roberto L.O .; D'Ottaviano, Itala M.L .; и Мундичи, Даниэле (2000), Алгебраические основы многозначного мышления. Дордрехт: Клувер. ISBN 0-7923-6009-5
• Фодор, Янош (2004), «Непрерывные слева t-нормы в нечеткой логике: обзор». Acta Polytechnica Hungarica 1(2), ISSN 1785-8860 [1]