WikiDer > Геометрия такси

Taxicab geometry

Геометрия такси в сравнении с евклидовым расстоянием: в геометрии такси красный, желтый и синий пути имеют одинаковую длину кратчайшего пути, равную 12. В евклидовой геометрии зеленая линия имеет длину.

{ displaystyle 6 { sqrt {2}} приблизительно 8,49}

и это единственный кратчайший путь.

А геометрия такси это форма геометрия в котором обычная функция расстояния или метрика из Евклидова геометрия заменяется новой метрикой, в которой расстояние между двумя точками - это сумма абсолютные различия от их Декартовы координаты. В метрика такси также известен как прямолинейное расстояние, L₁ расстояние, L¹ расстояние или ${ displaystyle ell _ {1}}$ норма (увидеть L^п Космос), змея расстояние, расстояние до городского квартала, Манхэттенское расстояние или Манхэттенская длина, с соответствующими вариациями в названии геометрии.^[1] Последние имена ссылаются на сетка большинства улиц на острове Манхэттен, который определяет кратчайший путь, по которому машина может пройти между двумя перекрестками в район иметь длину, равную расстоянию перекрестков в геометрии такси.

Геометрия использовалась в регрессивный анализ с 18 века, и сегодня его часто называют ЛАССО. Геометрическая интерпретация датируется неевклидова геометрия 19 века и связано с Герман Минковски.

Формальное определение

Расстояние такси, ${ displaystyle d_ {1}}$ , между двумя векторами ${ Displaystyle mathbf {p}, mathbf {q}}$ в п-размерный настоящий векторное пространство с фиксированной Декартова система координат, - сумма длин выступов отрезок между точками на оси координат. Более формально

{ Displaystyle d_ {1} ( mathbf {p}, mathbf {q}) = | mathbf {p} - mathbf {q} | _ {1} = sum _ {i = 1} ^ {n} | p_ {i} -q_ {i} |,}

где ${ Displaystyle ( mathbf {p}, mathbf {q})}$ находятся векторов

{ displaystyle mathbf {p} = (p_ {1}, p_ {2}, dots, p_ {n}) { text {and}} mathbf {q} = (q_ {1}, q_ {2 }, точки, q_ {n}) ,}

Например, в самолет, расстояние такси между ${ displaystyle (p_ {1}, p_ {2})}$ и ${ displaystyle (q_ {1}, q_ {2})}$ является ${ displaystyle | p_ {1} -q_ {1} | + | p_ {2} -q_ {2} |.}$

Свойства

Расстояние такси зависит от вращение системы координат, но не зависит от ее отражение вокруг координатной оси или ее перевод. Геометрия такси удовлетворяет всем Аксиомы Гильберта (формализация Евклидова геометрия) за исключением аксиома стороны-угла-стороны, поскольку два треугольника с одинаковыми «длинными» сторонами и одинаковым углом между ними обычно не конгруэнтный если только указанные стороны не параллельны.

Круги

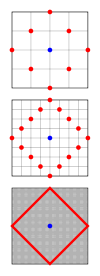
Круги в дискретной и непрерывной геометрии такси

А круг представляет собой набор точек с фиксированным расстоянием, называемый радиус, из точки, называемой центр. В геометрии такси расстояние определяется другой метрикой, чем в евклидовой геометрии, и форма кругов также изменяется. Круги такси квадраты со сторонами, ориентированными под углом 45 ° к осям координат. На изображении справа показано, почему это так, красным цветом показаны все точки с фиксированным расстоянием от центра, показанные синим цветом. По мере уменьшения размеров городских кварталов количество точек становится больше, и они превращаются в повернутый квадрат в непрерывной геометрии такси. Хотя каждая сторона будет иметь длину ${ displaystyle { sqrt {2}} r}$ с помощью Евклидова метрика, где р - радиус круга, его длина в геометрии такси равна 2р. Таким образом, длина окружности равна 8р. Таким образом, значение геометрического аналога ${ displaystyle pi}$ равно 4 в этой геометрии. Формула для единичного круга в геометрии такси: ${ displaystyle | x | + | y | = 1}$ в Декартовы координаты и

{ Displaystyle г = { гидроразрыва {1} {| грех тета | + | соз тета |}}}

в полярные координаты.

Окружность радиуса 1 (на этом расстоянии) - это район фон Неймана своего центра.

Круг радиуса р для Чебышевская дистанция (L_∞ метрика) на плоскости также есть квадрат со стороной 2р параллельно осям координат, поэтому планарное расстояние Чебышева можно рассматривать как эквивалентное путем вращения и масштабирования до планарного расстояния такси. Однако эта эквивалентность L₁ и я_∞ показатели не распространяются на более высокие измерения.

Всякий раз, когда каждая пара в наборе этих кругов имеет непустое пересечение, существует точка пересечения для всего набора; следовательно, расстояние Манхэттена образует инъективное метрическое пространство.

Приложения

Меры дистанций в шахматах

В шахматы, расстояние между квадратами на шахматная доска для грачи измеряется расстоянием такси; короли и королевы использовать Чебышевская дистанция, и епископы используйте расстояние такси (между квадратами одного цвета) на шахматной доске, повернутой на 45 градусов, то есть с ее диагоналями в качестве осей координат. Чтобы добраться от одной клетки до другой, только короли требуют, чтобы количество ходов было равно их соответствующему расстоянию; для ладей, ферзей и слонов требуется один-два хода (на пустой доске и при условии, что этот ход вообще возможен в случае слона).

Сжатое зондирование

При решении недоопределенная система линейных уравнений регуляризация член для вектора параметров выражается через ${ displaystyle ell _ {1}}$ -норма (геометрия такси) вектора.^[2] Этот подход появляется в структуре восстановления сигнала, называемой сжатое зондирование.

Отличия частотных распределений

Геометрию такси можно использовать для оценки различий в дискретных частотных распределениях. Например, в Сплайсинг РНК позиционное распределение гексамеры, которые показывают вероятность появления каждого гексамера в каждом заданном нуклеотид рядом с местом стыка, можно сравнить с расстоянием L1. Каждое распределение положений может быть представлено в виде вектора, где каждая запись представляет вероятность того, что гексамер начинается с определенного нуклеотида. Большое расстояние L1 между двумя векторами указывает на значительную разницу в характере распределений, в то время как небольшое расстояние указывает на распределения схожей формы. Это эквивалентно измерению площади между двумя кривыми распределения, поскольку площадь каждого сегмента представляет собой абсолютную разницу между вероятностями двух кривых в этой точке. При суммировании для всех сегментов он дает ту же меру, что и расстояние L1.^[3]

История

В L¹ метрика использовалась в регрессивный анализ в 1757 г. Роджер Джозеф Боскович.^[4] Геометрическая интерпретация датируется концом 19 века и развитием неевклидовы геометрии, в частности Герман Минковски и его Неравенство Минковского, из которых эта геометрия является частным случаем, особенно используемым в геометрия чисел, (Минковский 1910). Формализация L^п пробелы зачисляется на (Рис 1910).

Смотрите также

Заметки

^ Блэк, Пол Э. "Манхэттенское расстояние". Словарь алгоритмов и структур данных. Получено 6 октября, 2019.
^ Донохо, Дэвид Л. (23 марта 2006 г.). "Для большинства больших недоопределенных систем линейных уравнений минимальный ${ displaystyle ell _ {1}}$ -нормальное решение также является самым редким решением ". Сообщения по чистой и прикладной математике. 59 (6): 797–829. Дои:10.1002 / cpa.20132.
^ Лим, Киан Хуат; Феррарис, Лучиана; Filloux, Madeleine E .; Рафаэль, Бенджамин Дж .; Fairbrother, Уильям Г. (5 июля 2011 г.). «Использование позиционного распределения для идентификации элементов сплайсинга и прогнозирования дефектов процессинга пре-мРНК в генах человека». Труды Национальной академии наук Соединенных Штатов Америки. 108 (27): 11093–11098. Bibcode:2011PNAS..10811093H. Дои:10.1073 / pnas.1101135108. ЧВК 3131313. PMID 21685335.
^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 г.. Издательство Гарвардского университета. ISBN 9780674403406. Получено 6 октября, 2019.

использованная литература

Краузе, Юджин Ф. (1987). Геометрия такси. Дувр. ISBN 978-0-486-25202-5.
Минковский, Германн (1910). Geometrie der Zahlen (на немецком). Лейпциг и Берлин: Р. Г. Тойбнер. JFM 41.0239.03. Г-Н 0249269. Получено 6 октября, 2019.
Рис, Фриджес (1910). "Untersuchungen über Systeme integrierbarer Funktionen". Mathematische Annalen (на немецком). 69 (4): 449–497. Дои:10.1007 / BF01457637. HDL:10338.dmlcz / 128558.

внешние ссылки

Вайсштейн, Эрик В. «Метрика такси». MathWorld.
Малькевич, Джо (1 октября 2007 г.). "Такси!". Американское математическое общество. Получено 6 октября, 2019.

[1] Блэк, Пол Э. "Манхэттенское расстояние". Словарь алгоритмов и структур данных. Получено 6 октября, 2019.

[2] Донохо, Дэвид Л. (23 марта 2006 г.). "Для большинства больших недоопределенных систем линейных уравнений минимальный ${ displaystyle ell _ {1}}$ -нормальное решение также является самым редким решением ". Сообщения по чистой и прикладной математике. 59 (6): 797–829. Дои:10.1002 / cpa.20132.

[lim-3] Лим, Киан Хуат; Феррарис, Лучиана; Filloux, Madeleine E .; Рафаэль, Бенджамин Дж .; Fairbrother, Уильям Г. (5 июля 2011 г.). «Использование позиционного распределения для идентификации элементов сплайсинга и прогнозирования дефектов процессинга пре-мРНК в генах человека». Труды Национальной академии наук Соединенных Штатов Америки. 108 (27): 11093–11098. Bibcode:2011PNAS..10811093H. Дои:10.1073 / pnas.1101135108. ЧВК 3131313. PMID 21685335.

[Stigler1986-4] Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 г.. Издательство Гарвардского университета. ISBN 9780674403406. Получено 6 октября, 2019.

[1]

[2]

[3]

[4]

Navigation