WikiDer > Теория трехфазного движения
Теория трехфазного движения это теория из транспортный поток разработан Борис Кернер с 1996 по 2002 гг.[1][2][3] Основное внимание в нем уделяется объяснению физики нарушения дорожного движения и возникающей в результате перегруженности автомагистралей. Кернер описывает три фазы трафика, в то время как классические теории, основанные на фундаментальной диаграмме транспортного потока, имеют две фазы: свободное течение и перегруженный трафик. Теория Кернера делит перегруженный трафик на две отдельные фазы: синхронизированный поток и широкая подвижная пробка, доведя общее количество фаз до трех:
- Свободное течение (F)
- Синхронизированный поток (S)
- Широкое подвижное застревание (J)
Слово «широкий» используется даже в том случае, если речь идет о длине пробки.
А фаза определяется как состояние в пространстве и времени.
Свободное течение (F)
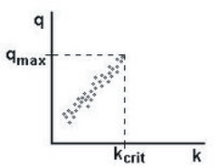
В условиях свободного транспортного потока эмпирические данные показывают положительный корреляция между скоростью потока (в транспортных средствах в единицу времени) и плотности транспортных средств (в транспортных средствах на единицу расстояния). Эта связь останавливается при максимальном свободном потоке с соответствующей критической плотностью . (См. Рисунок 1.)
Перегруженный трафик
Данные показывают более слабую связь между потоком и плотностью в условиях перегруженности. Таким образом, Кернер утверждает, что фундаментальная диаграмма, используемый в классической теории дорожного движения, не может адекватно описать сложную динамику автомобильного движения. Вместо этого он делит скопление на синхронизированный поток и широкие подвижные пробки.
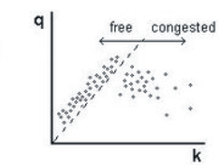
В загруженном транспортном потоке скорость автомобиля ниже минимальной скорости автомобиля. встречается в свободном потоке, т. е. на линии с наклоном минимальной скорости в свободном потоке (пунктирная линия на рисунке 2) разделяет эмпирические данные на плоскости плотности потока на две области: слева точки данных свободного потока и справа точки данных, соответствующие перегруженному трафику.
Определения [J] и [S] фаз J и S в загруженном трафике
В теории Кернера фазы J и S в загруженном трафике наблюдаются результаты во всех пространственно-временные особенности реальных данных трафика. Фазы J и S определены через определения [J] и [S] следующее:
Фаза «широкого движущегося затора» [J]
Так называемая «широкая пробка» движется вверх по течению по любой магистрали. узкие места. При этом средняя скорость фронта вниз по потоку поддерживается. Это характерная особенность широкого движущегося заедания, определяющая фазу J.
Период, термин широкая подвижная пробка предназначен для отражения характерной особенности пробки, распространяющейся через любое другое состояние транспортного потока и через любые горлышко бутылки при сохранении скорости нижнего фронта затора. Фраза движущийся джем отражает распространение затора в целом локализованную структуру на дороге. Чтобы отличить широкие движущиеся заторы от других движущихся заторов, которые обычно не поддерживают среднюю скорость фронта затора ниже по потоку, Кернер использовал термин широкий. Период, термин широкий отражает тот факт, что если движущийся затор имеет ширину (в продольном направлении дороги), значительно превышающую ширину фронтов затора, и если скорость транспортного средства внутри затора равна нулю, затор всегда проявляет характерную особенность поддержания скорости переднего фронта застревания (см. п. 7.6.5 книги[4]Таким образом, термин широкий не имеет ничего общего с шириной варенья, но на самом деле относится к его длине, которая значительно больше, чем переходные зоны на его голове и хвосте. Исторически Кернер использовал термин широкий из качественной аналогии широкой движущейся пробки в транспортном потоке с широкий автосолитоны встречающиеся во многих системах естествознания (например, газовая плазма, электронно-дырочная плазма в полупроводниках, биологические системы и химические реакции): как широкая движущаяся блокировка, так и широкий автосолитон обладают некоторыми характерными особенностями, которые не зависят от начальных условий, при которых эти локализованные шаблоны произошли.
Фаза «синхронизированного потока» [S]
В «синхронизированном потоке» нижний фронт, где транспортные средства ускоряются до свободного потока, не демонстрирует этой характерной особенности широкого движущегося затора. В частности, нижний фронт синхронизированного потока часто фиксируется в узком месте.
Термин «синхронизированный поток» предназначен для отражения следующих характеристик этой фазы движения: (i) Это непрерывный поток движения без значительных остановок, как это часто бывает внутри широкой движущейся пробки. Термин «поток» отражает эту особенность. (ii) В этом потоке наблюдается тенденция к синхронизации скоростей транспортных средств по разным полосам движения на многополосной дороге. Кроме того, существует тенденция к синхронизации скоростей транспортных средств на каждой из полос движения (скопление транспортных средств) в синхронизированном потоке. Это связано с относительно низкой вероятностью прохождения. Термин «синхронизированный» отражает этот эффект синхронизации скорости.
Объяснение определений фаз трафика на основе измеренных данных трафика
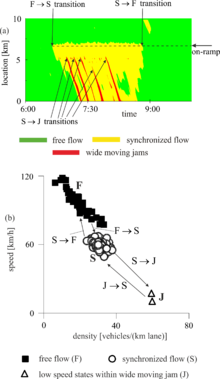
Измеренные данные об усредненных скоростях транспортного средства (рис. 3 (а)) иллюстрируют определения фаз [J] и [S]. На Рисунке 3 (а) показаны две пространственно-временные модели загруженного движения с низкой скоростью транспортных средств. Один паттерн распространяется вверх по потоку с почти постоянной скоростью нижнего фронта, двигаясь прямо через узкое место на автостраде. Согласно определению [J], эта модель скопления относится к фазе «широкого движущегося затора». Напротив, нижний фронт другого рисунка фиксируется в узком месте. Согласно определению [S], этот паттерн принадлежит к фазе «синхронизированного потока» (рис. 3 (а) и (б)). Другие эмпирические примеры проверки определений фазы трафика [J] и [S] можно найти в книгах[4] и,[5][6] в статье[7] а также в эмпирическом исследовании данные плавающего автомобиля[8] (данные о плавающих автомобилях также называются данные о транспортном средстве).
Определение фазы движения на основе эмпирических данных об одном транспортном средстве
В разд. 6.1 книги[5] было показано, что определения фазы трафика [S] и [J] являются источником большинства гипотез трехфазной теории и связанных с ней трехфазных микроскопических моделей транспортных потоков. Определения фазы трафика [J] и [S] являются нелокальными макроскопическими, и они применимы только после того, как макроскопические данные были измерены в пространстве и времени, то есть в "автономном" исследовании. Это связано с тем, что для окончательного различия фаз J и S через определения [J] и [S] необходимо изучение распространения заторов через узкое место. Это часто считается недостатком определений фазы трафика [S] и [J]. Однако существуют локальные микроскопические критерии различения фаз. J и S без изучения распространения перегруженного трафика через узкое место. Микроскопические критерии таковы (см. Раздел 2.6 книги[5]): Если в одиночном автомобиле (микроскопический) данные, относящиеся к перегруженному движению, "интервал прерывания потока", то есть наблюдается временной интервал между двумя автомобилями, следующими друг за другом, который намного больше, чем средняя временная задержка ускорения транспортного средства из широкой движущейся пробки (последняя составляет примерно 1,3–2,1 с), то соответствующий интервал прерывания потока соответствует фазе широкого движущегося затора. После того, как по этому критерию в перегруженном трафике были обнаружены все широкие движущиеся пробки, все оставшиеся перегруженные состояния связаны с фазой синхронизированного потока.
Гипотеза Кернера о двумерных (2D) состояниях транспортного потока
Устойчивые состояния синхронизированного потока
Однородный синхронизированный поток - это гипотетический состояние синхронизированного потока идентичных транспортных средств и водителей, в котором все транспортные средства движутся с одинаковой, не зависящей от времени скоростью и имеют одинаковые промежутки в пространстве (промежуток - это расстояние между одним транспортным средством и тем, что находится за ним), т. е. этот синхронизированный поток равен однородный во времени и пространстве.
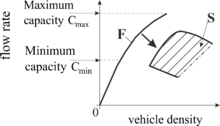
Гипотеза Кернера состоит в том, что однородный синхронизированный поток может возникать где угодно в двумерной области (2D) плоскости плотности потока (2D-область S на рисунке 4 (а)). Набор возможных состояний свободного потока (F) перекрывает по плотности транспортного средства набор возможных состояний однородного синхронизированного потока. Состояния свободного потока на многополосной дороге и состояния однородного синхронизированного потока разделены промежутком в расходе и, следовательно, промежутком в скорости при заданной плотности: при каждой заданной плотности синхронизированная скорость потока ниже чем скорость свободного потока.
В соответствии с этой гипотезой трехфазной теории Кернера, при заданной скорости в синхронизированном потоке водитель может сделать произвольный выбор Что касается промежутка в пространстве по отношению к предыдущему транспортному средству, в пределах диапазона, связанного с двухмерной областью однородного синхронизированного потока (рис. 4 (b)): водитель принимает разные промежутки в пространстве в разное время и не использует какой-то один уникальный промежуток.

Гипотеза трехфазной теории движения Кернера о двухмерной области устойчивых состояний синхронизированного потока противоречит гипотезе более ранних теорий транспортных потоков, включающих принципиальная схема транспортного потока, которые предполагают одномерную зависимость между плотностью транспортного средства и расходом.
Следование за автомобилем в теории трехфазного движения
Согласно трехфазной теории Кернера, транспортное средство ускоряется, когда пространство к предыдущему автомобилю больше, чем зазор в пространстве синхронизации , я ем (помечено ускорение на рисунке 5); автомобиль замедляется, когда разрыв грамм меньше безопасного пространства , я ем (помечено замедление на рисунке 5).

Если зазор меньше грамм, водитель стремится адаптировать свою скорость к скорости движущегося впереди автомобиля, не заботясь о точном зазоре, при условии, что этот зазор не меньше безопасного зазора. (помечено адаптация скорости на рисунке 5). Таким образом, космический разрыв в соответствии с трехфазной теорией Кернера в автомобиле может быть любой космический зазор в диапазоне пространственного зазора. .
Автономное вождение в рамках теории трехфазного движения
В рамках трехфазной теории гипотеза о двумерных областях состояний синхронизированного потока также была применена для разработки модели автономное вождение автомобиль (также называемый автоматизированное вождение, беспилотный или автономный автомобиль).[9]
Распределение трафика - a F → S фаза перехода
Согласно данным измерений, заторы на дорогах чаще всего возникают вблизи узких мест на автомагистралях, например, на съездах, съездах или дорожных работах. Переход от свободного потока к перегруженному трафику известен как нарушение трафика. В теории трехфазного трафика Кернера разрушение трафика объясняется фазовым переходом от свободного потока к синхронизированному потоку (так называемый фазовый переход F → S). Это объяснение подтверждается доступными измерениями, поскольку в измеренных данных трафика после сбоя трафика в узком месте нижний фронт перегруженного трафика фиксируется в узком месте. Следовательно, возникающий в результате перегрузки трафика после его сбоя удовлетворяет определению [S] фазы «синхронизированного потока».
Эмпирические спонтанные и индуцированные F → S переходы
Кернер отмечает, используя эмпирические данные, что синхронизированный поток может образовываться в свободном потоке самопроизвольно (спонтанный фазовый переход F → S) или может быть вызван извне (индуцированный фазовый переход F → S).
Спонтанный фазовый переход F → S означает, что пробой происходит, когда до этого был свободный поток в узком месте, а также как вверх, так и после него. Это означает, что спонтанный фазовый переход F → S происходит за счет роста внутреннего возмущения свободного потока в окрестности узкого места.
Напротив, индуцированный фазовый переход F → S происходит через область перегруженного движения, которая первоначально возникла в другом месте дороги ниже по течению от узкого места. Обычно это происходит в связи с распространением области синхронизированного потока вверх по потоку или широкой движущейся пробкой. Эмпирический пример вызванного пробоя в узком месте, ведущего к синхронизированному потоку, можно увидеть на рисунке 3: синхронизированный поток возникает в результате распространения широкого движущегося затора вверх по потоку. Существование эмпирического вызванного пробоя трафика (т. Е. Эмпирического индуцированного F → S фазы переход) означает, что фазовый переход F → S происходит в метастабильный состояние свободного потока на узком месте магистрали. Период, термин метастабильный Свободный поток означает, что, когда в свободном потоке возникают небольшие возмущения, состояние свободного потока остается стабильным, то есть свободный поток сохраняется в узком месте. Однако, когда большие возмущения возникают в свободном потоке вблизи узкого места, свободный поток становится нестабильным, и синхронизированный поток возникает в узком месте.
Физическое объяснение пробоя трафика в трехфазной теории
Кернер объясняет природу фазовых переходов F → S конкуренцией «адаптации к скорости» и «чрезмерного ускорения». Адаптация к скорости определяется как замедление транспортного средства до скорости более медленного движущегося впереди транспортного средства. Чрезмерное ускорение определяется как ускорение транспортного средства, даже если предыдущее транспортное средство не движется быстрее, чем транспортное средство, а предыдущее транспортное средство дополнительно не ускоряется. В теории Кернера вероятность чрезмерного ускорения является прерывистой функцией скорости транспортного средства: при одинаковой плотности транспортного средства вероятность чрезмерного ускорения в свободном потоке больше, чем в синхронизированном потоке. Когда в пределах локального возмущения скорости адаптация скорости сильнее, чем чрезмерное ускорение, происходит фазовый переход F → S. В противном случае, когда чрезмерное ускорение сильнее адаптации скорости, начальное возмущение со временем затухает. В области синхронизированного потока сильное избыточное ускорение отвечает за возвратный переход от синхронизированного потока к свободному потоку (переход S → F).
Механизмов перегрузки автомобиля может быть несколько. Можно предположить, что на многополосной дороге наиболее вероятным механизмом чрезмерного ускорения является смена полосы движения на более быструю. В этом случае фазовые переходы F → S объясняются взаимодействием ускорения, а обгон более медленное транспортное средство (чрезмерное ускорение) и замедление до скорости более медленного транспортного средства впереди (адаптация скорости). Обгон способствует поддержанию свободного потока. «Адаптация скорости», с другой стороны, приводит к синхронизированному потоку. Если обгон невозможен, произойдет адаптация скорости. Кернер утверждает, что вероятность обгона прерванная функция плотности транспортного средства (Рисунок 6): при данной плотности транспортного средства вероятность обгона в свободном потоке намного выше, чем в синхронизированном потоке.
Обсуждение объяснения Кернером пробоя трафика
Объяснение Кернером нарушения дорожного движения в узком месте автомагистрали фазовым переходом F → S в метастабильном свободном потоке связано со следующими фундаментальными эмпирическими характеристиками нарушения дорожного движения в узком месте, обнаруженными в реальных измеренных данных: (i) Спонтанное нарушение дорожного движения в начальном свободный поток в узком месте приводит к появлению перегруженного трафика, входящий фронт которого фиксируется в узком месте (по крайней мере, в течение некоторого интервала времени), т. е. этот перегруженный трафик удовлетворяет определению [S] для фазы синхронизированного потока. Другими словами, самопроизвольный сбой трафика всегда является фазовым переходом F → S. (ii) Вероятность этого спонтанного нарушения движения является возрастающей функцией скорости потока в узком месте. (iii) В одном и том же узком месте нарушение трафика может быть спонтанным или индуцированным (см. эмпирические примеры этих фундаментальных особенностей распределения трафика в разделах 2.2.3 и 3.1 книги).[5]); по этой причине фазовый переход F → S происходит в метастабильный свободный поток в узком месте шоссе. Как объяснялось выше, смысл термина метастабильный свободный поток выглядит следующим образом. Достаточно малые возмущения в метастабильном распаде свободного потока. Однако, когда в узком месте возникает достаточно большое возмущение, происходит фазовый переход F → S. Такое возмущение, которое инициирует фазовый переход F → S в метастабильном свободном потоке в узком месте, можно назвать ядром срыва трафика. Другими словами, реальный пробой трафика (фазовый переход F → S) на узком месте шоссе демонстрирует зарождение природа. Кернер рассматривает эмпирическую природу зарождения нарушения дорожного движения (фазовый переход F → S) в узком месте дороги как эмпирическую основу науки о дорожном движении и транспорте.
Причина теории Кернера и его критики классических теорий транспортных потоков
Эмпирический характер зарождения нарушения дорожного движения в узких местах на шоссе не может быть объяснен классическими теориями и моделями дорожного движения. Поиск объяснения эмпирической природы зародышеобразования при разрыве трафика (фазовый переход F → S) в узком месте шоссе стал причиной развития трехфазной теории Кернера.
В частности, в двухфазных моделях транспортных потоков, в которых разбивка трафика связана с нестабильностью свободного потока, эта нестабильность модели приводит к фазовому переходу F → J, т.е. в этих моделях транспортного потока нарушение трафика определяется спонтанным возникновением широкого движения. заторы в начальном свободном потоке (см. критику Кернера по таким двухфазным моделям, а также по другим классическим моделям и теориям транспортных потоков в главе 10 книги[5] а также в критических обзорах,[10][11][12]).
Основное предсказание трехфазной теории Кернера
Кернер разработал трехфазную теорию как объяснение эмпирической природы нарушения дорожного движения в узких местах шоссе: случайный (вероятностный) фазовый переход F → S, который происходит в метастабильном состоянии свободного потока. Херуит Кернер объяснил главное предсказание, что эта метастабильность свободного течения относительно фазового перехода F → S определяется зарождающейся природой неустойчивости синхронизированного течения. Объяснение этому - достаточно большое локальное увеличение скорости в синхронизированном потоке (называемое нестабильностью S → F), то есть растущая волна скорости локального увеличения скорости в синхронизированном потоке в узком месте. Развитие неустойчивости S → F приводит к локальному фазовому переходу от синхронизированного потока к свободному течению в узком месте (переход S → F). Для объяснения этого явления Кернер разработал микроскопическую теорию S → F-неустойчивости.[13]
Ни одна из классических теорий и моделей транспортных потоков не учитывает S → F-нестабильность трехфазной теории.
Основной результат трехфазной теории о зарождающейся природе нарушения трафика (переход F → S) показывает, что трехфазная теория несоизмерима со всеми более ранними теориями и моделями транспортных потоков (см. Пояснения ниже).
Как уже упоминалось, основной причиной теории трехфазного трафика Кернера является объяснение эмпирической природы зарождения сбоев трафика (переход F → S) в узком месте. Для достижения этой цели в перегруженном трафике была введена новая фаза трафика, называемая синхронизированным потоком. Основная особенность фазы синхронизированного потока движения, сформулированная в теории трехфазного движения, приводит к зарождающейся природе перехода F → S. В этом смысле синхронизированная фаза движения потока Кернера, которая обеспечивает зарождающуюся природу перехода F → S в узком месте на шоссе, и теория трехфазного движения Кернера могут считаться синонимами.
Первоначально разработанный для дорожного движения, Кернер расширил теорию трех фаз для описания городского движения в 2011–2014 годах.[14][15]
Диапазон пропускной способности магистрали
В теории трехфазного трафика нарушение трафика объясняется переходом F → S, происходящим в метастабильный свободное течение. Вероятно, наиболее важным последствием этого является наличие диапазона пропускной способности магистрали от максимальной до минимальной.
Максимальная и минимальная пропускная способность шоссе
Самопроизвольный срыв трафика, т.е. самопроизвольный фазовый переход F → S, может происходить в широком диапазоне расходов в свободном потоке. Кернер утверждает, основываясь на эмпирических данных, что из-за возможности спонтанных или вызванных сбоев движения на том же узком месте автострады в любой момент узкое место занимает несколько магистралей. Этот диапазон пропускной способности автострады находится между минимальной пропускной способностью. и максимальная вместимость свободного потока (рисунок 7).
Шоссе мощности и метастабильность свободного потока
Максимальная пропускная способность трассы : Если расход близок к максимальной производительности , то даже небольшие возмущения свободного потока в узком месте приведут к спонтанному фазовому переходу F → S. С другой стороны, только очень большие возмущения свободного потока в узком месте приведут к спонтанному фазовому переходу F → S, если скорость потока близка к минимальной. (см., например, п. 17.2.2 книги[4]). Вероятность меньшего нарушения свободного потока намного выше, чем вероятность большего нарушения. Следовательно, чем выше скорость потока в свободном потоке в узком месте, тем выше вероятность спонтанного фазового перехода F → S. Если расход в свободном потоке ниже минимальной производительности , в узком месте не будет сбоев трафика (без фазового перехода F → S).
Бесконечное количество пропускных способностей магистралей в узких местах можно проиллюстрировать метастабильностью свободного потока при расходах. с
Метастабильность свободного потока означает, что при малых возмущениях свободный поток остается стабильным (свободный поток сохраняется), но при больших возмущениях поток становится нестабильным и происходит фазовый переход F → S в синхронизированный поток.
Обсуждение определений емкости
Таким образом, основной теоретический результат трехфазной теории о понимании стохастической пропускной способности свободного потока в узком месте выглядит следующим образом: В любой момент, в узком месте находится бесконечное количество пропускных способностей магистрали свободного потока. Бесконечное количество скоростей потока, при которых может возникнуть нарушение движения в узком месте, - это бесконечное количество пропускных способностей магистрали. Эти мощности находятся в диапазоне расхода от минимальной до максимальной (Рисунок 7).
Диапазон пропускной способности шоссе в узком месте в теории трехфазного движения Кернера в корне противоречит классическому пониманию стохастической пропускной способности шоссе, а также теориям и методам управления движением и управлению движением, которые в любое время предполагают существование частности пропускная способность шоссе. Напротив, в теории трехфазного трафика Кернера в любое время существует диапазон пропускной способности магистрали, которая находится между минимальной пропускной способностью и максимальная мощность . Ценности и может существенно зависеть от параметров движения (процент длинных транспортных средств в транспортном потоке, погодные условия, характеристики узких мест и т. д.).
Существование в любой момент Теория Кернера, определяющая пропускную способность различных магистралей, в корне меняет методологии управления движением, динамического распределения и управления движением. В частности, чтобы удовлетворить зарождающуюся природу сбоя трафика, Кернер ввел принцип минимизации пробоев (Принцип BM) для оптимизации и управления транспортными сетями.
Широкие подвижные застревания (J)
Движущееся застревание назовем «широким», если его длина (в направлении потока) явно превышает длину фронтов застревания. Средняя скорость автомобиля в широких движущихся заторах намного ниже средней скорости в свободном потоке. Внизу по потоку автомобили разгоняются до скорости свободного потока. На переднем фронте затора транспортные средства идут со свободным или синхронным потоком и должны снизить свою скорость. Согласно определению [J] широкий движущийся затор всегда имеет одинаковую среднюю скорость выходного фронта , даже если пробка распространяется через другие фазы трафика или узкие места. В широком движущемся заторе скорость потока резко снижается.
Характерные параметры широких подвижных заторов
Эмпирические результаты Кернера показывают, что некоторые характерные черты широких движущихся заторов не зависят от объема трафика и характеристик узких мест (например, где и когда образовалась затор). Однако эти характерные особенности зависят от погодных условий, дорожных условий, технологии транспортного средства, процента длинномерных транспортных средств и т. Д. Скорость движения впереди широкого движущегося затора. (в восходящем направлении) является характеристическим параметром, как и расход сразу после затора. (со свободным потоком в этом месте, см. рисунок 8). Это означает, что многие широкие подвижные заторы в одинаковых условиях имеют схожие характеристики. Эти параметры относительно предсказуемы. Движение фронта затора ниже по потоку можно проиллюстрировать в плоскости плотности потока линией, которая называется «линией J» (линия J на рисунке 8). Наклон линии J - это скорость фронта затора ниже по потоку. .
Минимальная пропускная способность трассы и отток из-за широкого движущегося затора
Кернер подчеркивает, что минимальная емкость и истечение широкого движущегося затора описать два качественно разные особенности свободного потока: минимальная производительность характеризует фазовый переход F → S в узком месте, т.е. пробой трафика. Напротив, вытекание широкого движущегося затора определяет условие существования широкой движущейся пробки, т. е. фазы движения J в то время как затор распространяется в свободном потоке: Действительно, если затор распространяется в свободном потоке (то есть как до, так и после затора возникают свободные потоки), то широкое движущееся затор может сохраняться, только когда затор втекает равно или больше оттока затора ; в противном случае варенье со временем растворится. В зависимости от параметров движения, таких как погода, процент длинных транспортных средств и т. Д., И характеристик узкого места, где может произойти фазовый переход F → S, минимальная пропускная способность может быть меньше (как на рисунке 8) или больше, чем выход замятия .
Синхронизированная фаза потока (S)
В отличие от широких движущихся заторов, как скорость потока, так и скорость транспортного средства могут значительно изменяться в фазе синхронизированного потока. Фронт синхронизированного потока ниже по потоку часто фиксируется в пространстве (см. Определение [S]), обычно в узком месте в определенном месте дороги. Скорость потока в этой фазе может оставаться аналогичной скорости потока в свободном потоке, даже если скорость транспортного средства резко снизится.
Поскольку синхронизированная фаза потока не имеет характерных особенностей фазы широкого движущегося затора JТеория трехфазного движения Кернера предполагает, что гипотетические однородные состояния синхронизированного потока покрывают двумерную область в плоскости плотности потока (пунктирные области на рисунке 8).
S → J фаза перехода
Широкие движущиеся заторы не возникают самопроизвольно в свободном потоке, но могут возникать в областях синхронизированного потока. Этот фазовый переход называется фазовым переходом S → J.
«Застревание без очевидной причины» - фазовые переходы F → S → J
В 1998 г.[1] Кернер обнаружил, что в реальных полевых данных о трафике возникновение широкой движущейся пробки в свободном потоке наблюдается как каскад фазовых переходов F → S → J (рисунок 9): сначала возникает область синхронизированного потока в области свободного потока. поток. Как объяснялось выше, такой фазовый переход F → S происходит в основном в узком месте. В фазе синхронизированного потока происходит дальнейшее «самосжатие», и плотность транспортного средства увеличивается, а скорость транспортного средства уменьшается. Это самосжатие называется «пинч-эффектом». В «защемленных» областях синхронизированного течения возникают узкие движущиеся заторы. Если эти узкие подвижные застревания увеличиваются, появляются широкие подвижные застревания, обозначенные S → J на Рисунке 9). Таким образом, широкие движущиеся пробки возникают позже, чем произошел перерыв в движении (переход F → S), и на другом участке дороги выше узкого места. Следовательно, когда фазовые переходы Кернера F → S → J, происходящие в реальном движении (рисунок 9 (a)), представлены в плоскости скорость-плотность (рисунок 9 (b)) (или в плоскости скорость-поток, или же в плоскости плотности потока) , следует помнить, что состояния синхронизированного потока и состояния низкой скорости в широком движущемся заторе измеряются в разных местах дороги. Кернер отмечает, что частота появления широких движущихся заторов увеличивается, если плотность синхронизированного потока увеличивается. Широкие движущиеся заторы распространяются дальше вверх по потоку, даже если они распространяются через области синхронизированного потока или узкие места. Очевидно, что также возможна любая комбинация обратных фазовых переходов (переходы S → F, J → S и J → F, показанные на рисунке 9).
Физика S → J переход
Для дальнейшей иллюстрации фазовых переходов S → J: в теории трехфазного движения Кернера линия J делит однородные состояния синхронизированного потока на две части (рис. 8). Состояния однородного синхронизированного потока над линией J метастабильны. Состояния однородного синхронизированного потока ниже линии J являются стабильными состояниями, в которых не может происходить фазовый переход S → J. Метастабильный однородный синхронизированный поток означает, что при небольших помехах состояние трафика остается стабильным. Однако, когда возникают большие возмущения, синхронизированный поток становится нестабильным и происходит фазовый переход S → J.
Схема движения S и J
Наблюдаются очень сложные картины скопления, вызванные фазовыми переходами F → S и S → J.
Классификация шаблонов синхронизированного потока трафика (SP)
Шаблон перегрузки синхронизированного потока (Synchronized Flow Pattern (SP)) с фиксированным нисходящим потоком и не непрерывно распространяющимся восходящим фронтом называется локализованным синхронизированным шаблоном потока (LSP).
Часто восходящий фронт SP распространяется вверх по течению. Если только восходящий фронт распространяется в восходящем направлении, связанный SP называется расширяющейся синхронизированной структурой потока (WSP). Фронт ниже по потоку остается узким местом, а ширина SP увеличивается.
Возможно, что и восходящий, и нисходящий фронт распространяются вверх по течению. Фронт ниже по потоку больше не является узким местом. Этот шаблон был назван шаблоном движущегося синхронизированного потока (MSP).
Эффект отлова синхронизированного потока на узком месте на шоссе
Разница между SP и широким движущимся затором становится очевидной в том, что, когда WSP или MSP достигают узкого места выше по потоку, может возникнуть так называемый «эффект захвата». SP будет пойман в узком месте, и в результате появится новая модель перегруженности. Широкая движущаяся пробка не будет застревать в узком месте и будет двигаться дальше вверх по потоку. В отличие от широких движущихся заторов, синхронизированный поток, даже если он движется как МСП, не имеет характерных параметров. Например, скорость нижнего фронта MSP может значительно различаться и может отличаться для разных MSP. Эти особенности SP и широких движущихся заторов являются следствием фазовых определений [S] и [J].
Общая картина перегруженного трафика (GP)
Часто встречающаяся модель перегрузки - это та, которая содержит обе фазы перегрузки, [S] и [J]. Такой узор с [S] и [J] называется общим шаблоном (GP). Эмпирический пример GP показан на Рисунке 9 (а).
Во многих инфраструктурах автострад узкие места очень близки друг к другу. Шаблон перегрузки, синхронизированный поток которого охватывает два или более узких места, называется расширенным шаблоном (EP). EP может содержать только синхронизированный поток (называемый ESP: Expanded Synchronized Flow Pattern), но обычно в синхронизированном потоке образуются широкие движущиеся заторы. В таких случаях EP называется EGP (расширенный общий шаблон) (см. Рисунок 10).
Применение теории трехфазного движения в транспортной технике
Одним из приложений теории трехфазного трафика Кернера являются методы, называемые ASDA / FOTO (Аutomatische SтауDynamikАnalyse (автоматическое отслеживание широких движущихся заторов) и Fдобыча руды Ож Трафтинг Оbjects). ASDA / FOTO - это программный инструмент, способный быстро и эффективно обрабатывать большие объемы данных о дорожном движении в сетях автострад (см. Примеры из трех стран, рисунок 11). ASDA / FOTO работает в онлайн-системе управления трафиком на основе измеренных данных трафика. Распознавание, отслеживание и прогнозирование [S] и [J] выполняются с использованием особенностей теории трехфазного трафика Кернера.
Дальнейшие применения теории видны в разработке имитационных моделей трафика, системы измерения скорости движения (ANCONA), коллективного управления дорожным движением, помощи при движении, автономного вождения и определения состояния дорожного движения, как описано в книгах Кернера.[4][5][6]
Математические модели транспортного потока в рамках теории трехфазного движения Кернера.
А не математическая модель из транспортный потокТрехфазная теория Кернера - это качественная теория транспортных потоков, состоящая из нескольких гипотез. Гипотезы трехфазной теории Кернера должны качественно объяснить пространственно-временные явления трафика в транспортных сетях, обнаруженные в реальных полевых данных о трафике, которые измерялись на протяжении многих лет на различных автомагистралях в разных странах. Некоторые из гипотез теории Кернера были рассмотрены выше. Можно ожидать, что большое количество разнообразных математические модели транспортного потока можно разработать в рамках трехфазной теории Кернера.
Первый математическая модель транспортного потока в рамках трехфазной теории Кернера, что математическое моделирование может показать и объяснить нарушение трафика фазовым переходом F → S в метастабильном свободном потоке в узком месте, была модель Кернера-Кленова, введенная в 2002 году.[16] Модель Кернера – Кленова - это микроскопическая стохастическая модель в рамках теории трехфазного движения Кернера. В модели Кернера-Кленова транспортные средства движутся в соответствии со стохастическими правилами движения транспортных средств, которые можно индивидуально выбрать для каждого из транспортных средств. Несколько месяцев спустя Кернер, Кленов и Вольф разработали клеточный автомат (CA) модель транспортного потока в рамках трехфазной теории Кернера.[17]
Стохастическая трехфазная модель транспортного потока Кернера-Кленова в рамках теории Кернера получила дальнейшее развитие для различных приложений, в частности, для моделирования учета на рампе, управления ограничением скорости, динамического распределения трафика в транспортных и транспортных сетях, трафика в тяжелых условиях. узкие места и движущиеся узкие места, особенности неоднородного транспортного потока, состоящего из разных транспортных средств и водителей, методы предупреждения о пробках, связь между транспортными средствами (V2V) для совместного вождения, производительность беспилотных транспортных средств в смешанном потоке движения, нарушение дорожного движения на сигналы в городском потоке, перенасыщенный городской транспорт, расход топлива автотранспортом в транспортных сетях (см. ссылки в п. 1.7 обзора[12]).
Со временем несколько научных групп разработали новые математические модели в рамках трехфазной теории Кернера. В частности, новые математические модели в рамках трехфазной теории Кернера были введены в работах Цзян, Ву, Гао и др.,[18][19] Дэвис,[20] Ли, Барлович, Шрекенберг и Ким[21] (другие ссылки на математические модели в рамках теории трехфазного трафика Кернера и результаты их исследований см. в разделе 1.7 обзора[12]).
Критика теории
Теорию критиковали по двум основным причинам. Во-первых, теория почти полностью основана на измерениях Bundesautobahn 5 в Германии. Может быть, эта дорога имеет такой же рисунок, но другие дороги в других странах имеют другие характеристики. Будущие исследования должны показать обоснованность теории на других дорогах в других странах мира. Во-вторых, неясно, как данные были интерполированный. Кернер использует измерения с фиксированной точкой (детекторы петель), но свои выводы делает по автомобилю траектории, которые охватывают всю исследуемую дорогу. Эти траектории можно измерить напрямую, только если данные плавающего автомобиля используется, но, как сказано, используются только измерения петлевого детектора. Как промежуточные данные были собраны или интерполированы, не ясно.
На приведенную выше критику был дан ответ в недавнем исследовании данных, измеренных в США и Великобритании, которое подтверждает выводы, сделанные на основе измерений на Bundesautobahn 5 в Германии.[7] Более того, недавно была подтверждена теория, основанная на данных о плавающих автомобилях.[22] В этой статье также можно найти методы пространственно-временной интерполяции данных, измеренных детекторами дороги (см. Приложения к статье).
Были высказаны и другие критические замечания, например, что понятие фаз не было четко определено и что так называемые двухфазные модели также успешно имитируют существенные особенности, описанные Кернером.[23]
На эту критику был дан ответ в обзоре[10] следующее. Наиболее важной особенностью теории Кернера является объяснение эмпирической природы зарождения пробоев на дороге в узком месте перехода F → S. Эмпирическая зарождающаяся природа нарушения трафика не можешь можно объяснить с помощью более ранних теорий транспортных потоков, включая двухфазные модели транспортных потоков, изученные в.[23]
Несоизмеримость теории трехфазного движения и классических теорий транспортных потоков
Объяснение нарушения дорожного движения в узком месте на шоссе переходом F → S в метастабильный свободный поток в узком месте является основным предположением трехфазной теории Кернера.[10] Тем не мение, никто из более ранних теорий транспортного потока включает переход F → S в метастабильный свободный поток в узком месте. Таким образом, ни одна из классических теорий транспортных потоков не согласуется с эмпирической природой зарождения реального пробоя трафика в узком месте на шоссе.
Фазовый переход F → S в метастабильном свободном потоке в узком месте магистрали действительно объясняет эмпирические свидетельства индуцированного перехода от свободного потока к синхронизированному потоку вместе с зависимостью вероятности разрушения от расхода. В соответствии с классической книгой Куна,[24] это показывает несоизмеримость трехфазной теории и классических теорий транспортных потоков (подробнее см.[25]):
Минимальная пропускная способность магистрали , при котором фазовый переход F → S все еще может быть вызван в узком месте на шоссе, как указано в теории Кернера, имеет нет смысл других теорий и моделей транспортных потоков.
Существование этих двух фаз F и S при той же скорости потока не является следствием стохастического характера движения: даже если в автомобильном движении не было стохастических процессов, состояния F и S существуют с той же скоростью потока. Однако классические стохастические подходы к управлению трафиком не предполагают возможность фазового перехода F → S в метастабильном свободном потоке. По этой причине эти стохастические подходы не могут решить проблему несовместимости классических теорий с зарождающейся природой реальных нарушений трафика.
По словам Кернера, это несоответствие может объяснить, почему подходы к оптимизации и управлению сетью, основанные на этих основах и методологиях, потерпели неудачу в своих приложениях в реальном мире. Даже несколько десятилетий очень интенсивных усилий по улучшению и проверке моделей оптимизации сети не увенчались успехом. Действительно, не существует примеров, когда онлайн-реализации моделей оптимизации сети, основанные на этих основах и методологиях, могли бы уменьшить перегрузку в реальных сетях трафика и транспортных сетях.
Это связано с тем, что фундаментальные эмпирические особенности распределения трафика на узких местах автомагистралей были изучены только в течение последних 20 лет. Напротив, общепринятые основы и методологии теории движения и транспорта были внедрены в 50–60-е годы. Примерами этой классической теории транспортных потоков являются модель Лайтхилла – Уизема – Ричардса (LWR),[26][27] Модель транспортного потока General Motors (GM) Германа, Газиса, Монтролла, Поттса и Ротери,[28][29] а также принципы Уордропа по оптимизации транспортных сетей.[30] Таким образом, ученые, чьи идеи привели к этим классическим основам и методологиям теории дорожного движения и транспорта, не могли знать зарождающуюся природу реальных нарушений дорожного движения. Многие из разнообразных поведенческих характеристик водителей, связанных с реальным трафиком, а также некоторые математические подходы к моделированию транспортных потоков, которые были обнаружены в классических подходах к теории транспортных потоков, также используются в теории трехфазного движения и связанных с ней микроскопических транспортных потоков. модели (подробнее см. раздел 11 обзора[10]).
Смена парадигмы в транспортной науке
Период, термин "несоизмеримость" упомянутое выше было введено Куном в его классической книге[24] объяснить смена парадигмы Смена парадигмы в науке о дорожном движении и транспорте - это фундаментальное изменение значения стохастической пропускной способности автомагистралей, поскольку значение пропускной способности автомагистралей является основой для разработки любого метода управления движением, управления и организации движения. сеть, а также приложения интеллектуальные транспортные системы[31][32][33][34][35]. Парадигма стандартных теорий дорожного движения и транспорта такова:[33][35] что в любой момент времени есть значение стохастической пропускной способности магистрали. Когда скорость потока в узком месте превышает значение пропускной способности в этот момент времени, в узком месте должен происходить сбой трафика.
Новая парадигма науки о дорожном движении и транспорте, вытекающая из эмпирической природы зародыша разрушения трафика (переход F → S) и теории трехфазного движения Кернера, в корне меняет смысл стохастической пропускной способности шоссе следующим образом[4][5][6][36][37]. В любой момент времени существует диапазон значений пропускной способности магистрали между минимальной и максимальной пропускной способностью магистрали, которые сами по себе являются стохастическими значениями. Когда скорость потока в узком месте находится в пределах диапазона пропускной способности, относящегося к данному моменту времени, нарушение трафика может произойти в узком месте только с некоторой вероятностью, то есть в некоторых случаях происходит сбой трафика, в других случаях этого не происходит.
Смотрите также
- Активное управление трафиком
- Принципиальная схема
- Интеллектуальная транспортная система
- Микроскопическая модель транспортного потока
- Узкое место трафика
- Транспортный поток
- Волна трафика
- Заторы на дорогах
- Пробки: реконструкция на основе трехфазной теории Кернера
- Принцип минимизации поломки Кернера
- Прогнозирование перевозок
Примечания
- ^ а б Кернер, Б. С (1998). «Экспериментальные особенности самоорганизации в транспортном потоке». Письма с физическими проверками. 81 (17): 3797–3800. Bibcode:1998ПхРвЛ..81.3797К. Дои:10.1103 / PhysRevLett.81.3797.
- ^ Кернер, Борис С (1999). «Физика дорожного движения». Мир физики. 12 (8): 25–30. Дои:10.1088/2058-7058/12/8/30.
- ^ Кернер, Борис (1999). «Перегруженный транспортный поток: наблюдения и теория». Отчет о транспортных исследованиях: журнал Совета по исследованиям в области транспорта. 1678: 160–167. Дои:10.3141/1678-20.
- ^ а б c d е Б.С. Кернер, Физика дорожного движения, Springer, Берлин, Нью-Йорк 2004[страница нужна]
- ^ а б c d е ж грамм Б.С. Кернер, Введение в современную теорию транспортных потоков и управление ими: долгий путь к теории трехфазного движения, Springer, Берлин, Нью-Йорк 2009
- ^ а б c Борис С. Кернер, «Разбивка транспортных сетей: основы транспортной науки», Springer, Берлин, 2017 г.[страница нужна]
- ^ а б Реборн, Хуберт; Кленов, Сергей Л; Палмер, Йохен (2011). «Эмпирическое исследование общих характеристик транспортных заторов на основе данных о дорожном движении, измеренных в США, Великобритании и Германии». Physica A: Статистическая механика и ее приложения. 390 (23–24): 4466. Bibcode:2011PhyA..390.4466R. Дои:10.1016 / j.physa.2011.07.004.
- ^ Р.-П. Шефер и др., «Исследование данных о транспортном средстве TomTom с использованием теории трехфазного движения». Управление дорожным движением, Том 52, № 5, страницы 225–231, 2011 г.
- ^ Кернер, Борис С (2018). «Физика автоматизированного вождения в рамках теории трехфазного движения». Физический обзор E. 97 (4): 042303. arXiv:1710.10852. Bibcode:2018PhRvE..97d2303K. Дои:10.1103 / PhysRevE.97.042303. PMID 29758629.
- ^ а б c d Кернер, Борис С (2013). «Критика общепринятых основ и методологий теории дорожного движения и транспорта: краткий обзор». Physica A: Статистическая механика и ее приложения. 392 (21): 5261–5282. Bibcode:2013PhyA..392.5261K. Дои:10.1016 / j.physa.2013.06.004.
- ^ Кернер, Борис С (2015). «Несостоятельность классических теорий транспортных потоков: критический обзор». Elektrotechnik und Informationstechnik. 132 (7): 417–433. Дои:10.1007 / s00502-015-0340-3.
- ^ а б c Кернер, Борис С (2016). «Несостоятельность классических теорий транспортных потоков: стохастическая пропускная способность шоссе и автоматическое вождение». Physica A: Статистическая механика и ее приложения. 450: 700–747. arXiv:1601.02585. Bibcode:2016PhyA..450..700K. Дои:10.1016 / j.physa.2016.01.034.
- ^ Кернер, Борис С (2015). «Микроскопическая теория нестабильности транспортного потока, определяющая нарушение движения в узких местах автомагистралей: нарастающая волна увеличения скорости в синхронизированном потоке». Физический обзор E. 92 (6): 062827. arXiv:1511.04912. Bibcode:2015PhRvE..92f2827K. Дои:10.1103 / PhysRevE.92.062827. PMID 26764764.
- ^ Кернер, Борис С (2011). «Физика пробок в городе». Физический обзор E. 84 (4): 045102. arXiv:1108.4310. Bibcode:2011PhRvE..84d5102K. Дои:10.1103 / PhysRevE.84.045102. PMID 22181213.
- ^ Кернер, Борис С (2014). «Трехфазная теория городского движения: движение синхронизированных схем потока в условиях недостаточной насыщенности городского движения по сигналам». Physica A: Статистическая механика и ее приложения. 397: 76–110. Bibcode:2014PhyA..397 ... 76K. Дои:10.1016 / j.physa.2013.11.009.
- ^ Кернер, Борис С; Кленов, Сергей Л (2002). «Микроскопическая модель фазовых переходов в транспортном потоке». Журнал физики A: математические и общие. 35 (3): L31. Дои:10.1088/0305-4470/35/3/102.
- ^ Кернер, Борис С; Кленов, Сергей Л; Вольф, Дитрих Э (2002). «Клеточный автоматный подход к теории трехфазного трафика». Журнал физики A: математические и общие. 35 (47): 9971. arXiv:cond-mat / 0206370. Bibcode:2002JPhA ... 35.9971K. Дои:10.1088/0305-4470/35/47/303.
- ^ Цзян, Руи; У, Цин-Сун (2004). «Пространственно-временные модели на изолированном въезде в новую модель клеточного автомата, основанную на теории трехфазного движения». Журнал физики A: математические и общие. 37 (34): 8197. Bibcode:2004JPhA ... 37.8197J. Дои:10.1088/0305-4470/37/34/001.
- ^ Гао, Кун; Цзян, Руи; Ху, Шоу-Синь; Ван, Бинг-Хун; У, Цин-Сун (2007). «Клеточно-автоматная модель со скоростной адаптацией в рамках трехфазной теории трафика Кернера». Физический обзор E. 76 (2): 026105. Bibcode:2007PhRvE..76b6105G. Дои:10.1103 / PhysRevE.76.026105. PMID 17930102.
- ^ Дэвис, Л. С. (2004). «Многополосное моделирование фаз движения». Физический обзор E. 69 (1 балл 2): 016108. Bibcode:2004PhRvE..69a6108D. Дои:10.1103 / PhysRevE.69.016108. PMID 14995668.
- ^ Ли, Хён Гын; Барлович, Роберт; Шрекенберг, Майкл; Ким, Дучул (2004). «Механическое ограничение против чрезмерной реакции человека, вызывающей перегруженные состояния дорожного движения». Письма с физическими проверками. 92 (23): 238702. arXiv:cond-mat / 0404315. Bibcode:2004PhRvL..92w8702L. Дои:10.1103 / PhysRevLett.92.238702. PMID 15245199.
- ^ Кернер, Борис С; Реборн, Хуберт; Шефер, Ральф-Петер; Кленов, Сергей Л; Палмер, Йохен; Лорковски, Стефан; Витте, Николаус (2013). «Динамика движения в эмпирических данных о транспортных средствах, изученных с помощью трехфазной теории: пространственно-временная реконструкция фаз движения и генерация предупреждающих сообщений о пробках». Physica A: Статистическая механика и ее приложения. 392 (1): 221–251. Bibcode:2013PhyA..392..221K. Дои:10.1016 / j.physa.2012.07.070.
- ^ а б Трейбер, Мартин; Кестинг, Арне; Хелбинг, Дирк (2010). «Теория трехфазного движения и двухфазные модели с фундаментальной схемой в свете стилизованных эмпирических фактов». Транспортные исследования, часть B: методологические. 44 (8–9): 983. arXiv:1004.5545. Bibcode:2010arXiv1004.5545T. CiteSeerX 10.1.1.186.2970. Дои:10.1016 / j.trb.2010.03.004.
- ^ а б Т.С. Кун, "Структура научных революций". Четвертый выпуск. (Издательство Чикагского университета, Чикаго, Лондон, 2012 г.)[страница нужна]
- ^ Кернер, Борис С; Кленов, Сергей Л; Шрекенберг, Майкл (2014). «Вероятностные физические характеристики фазовых переходов на узких местах автомагистралей: несоизмеримость трехфазной и двухфазной теории транспортных потоков». Физический обзор E. 89 (5): 052807. Bibcode:2014PhRvE..89e2807K. Дои:10.1103 / PhysRevE.89.052807. PMID 25353844.
- ^ Лайтхилл, М. Дж .; Уизем, Г. Б. (1955). «О кинематических волнах. II. Теория транспортных потоков на длинных переполненных дорогах». Труды Королевского общества A: математические, физические и инженерные науки. 229 (1178): 317. Bibcode:1955RSPSA.229..317L. Дои:10.1098 / rspa.1955.0089.
- ^ Ричардс, Павел I (1956). «Ударные волны на шоссе». Исследование операций. 4: 42–51. Дои:10.1287 / opre.4.1.42.
- ^ Герман, Роберт; Montroll, Elliott W; Поттс, Ренфри Б.; Ротери, Ричард У (1959). «Динамика движения: анализ устойчивости при следовании за автомобилем». Исследование операций. 7: 86–106. Дои:10.1287 / opre.7.1.86.
- ^ Газис, Денос С; Герман, Роберт; Ротери, Ричард У (1961).«Нелинейные модели транспортного потока с опорой на лидера». Исследование операций. 9 (4): 545. Дои:10.1287 / opre.9.4.545.
- ^ Уордроп, Дж. Г. (1952). «Дорожная бумага. Некоторые теоретические аспекты исследования дорожного движения». Труды института инженеров-строителей. 1 (3): 325–362. Дои:10.1680 / ipeds.1952.11259.
- ^ А. Д. Мэй, Основы движения трафика, Prentice-Hall, Inc., Englewood Cliffs, 1990 г.
- ^ Н. Х. Гартнер, К. Дж. Мессер, А. Рати (редакторы) Теория транспортных потоков: новейший отчет. Совет транспортных исследований, Вашингтон, округ Колумбия, 2001 г.
- ^ а б Руководство по пропускной способности шоссе, Шестое издание, Национальный исследовательский совет. Совет по транспортным исследованиям, Вашингтон, округ Колумбия, 2016 г.
- ^ Р. П. Рёсс, E.S. Прассас, Руководство по пропускной способности шоссе: концептуальная история и история исследований, Springer, Берлин, 2014 г.
- ^ а б Л. Элефтериаду, Введение в теорию транспортного потока. Оптимизация Springer и ее приложения, том 84. Springer, Берлин, 2014 г.
- ^ Б.С. Кернер (ред.), Комплексная динамика управления трафиком, Серия «Энциклопедия сложности и системологии», Springer, Berlin, New York, 2019
- ^ Б.С. Кернер, «Комплексная динамика управления: введение», Springer Science + Business Media LLC, R.A. Мейерс (ред.), Энциклопедия сложности и системологии, Springer, Берлин (2019). DOI: 10.1007 / 978-3-642-27737-5_78-3
Рекомендации
- Лье, Генри (2005). «Физика дорожного движения: эмпирические особенности схемы автострад, инженерные приложения и теория». Физика сегодня. 58 (11): 54–56. Bibcode:2005ФТ .... 58к..54К. Дои:10.1063/1.2155762.
- Гао, Кун; Цзян, Руи; Ху, Шоу-Синь; Ван, Бинг-Хун; У, Цин-Сун (2007). «Клеточно-автоматная модель со скоростной адаптацией в рамках трехфазной теории трафика Кернера». Физический обзор E. 76 (2): 026105. Bibcode:2007PhRvE..76b6105G. Дои:10.1103 / PhysRevE.76.026105. PMID 17930102.
- Шёнхоф, Мартин; Хелбинг, Дирк (2009). «Критика теории трехфазного движения» (PDF). Транспортные исследования, часть B: методологические. 43 (7): 784. CiteSeerX 10.1.1.475.3565. Дои:10.1016 / j.trb.2009.02.004.
- Х. Реборн, С. Кленов, "Прогнозирование загруженных шаблонов трафика", В: Р. Мейерс (Ред.): Энциклопедия сложности и системологии, Springer, Нью-Йорк, 2009.
- Х. Реборн, Дж. Палмер, «Использование ASDA и FOTO для генерации сообщений трафика RDS / TMC», Traffic Engineering and Control, июль 2008 г., стр. 261–266.
- Дэвис, Л. Крейг (2010). «Введение в современную теорию и управление транспортными потоками: долгий путь к теории трехфазного движения». Физика сегодня. 63 (3): 53. Bibcode:2010ФТ .... 63с..53К. Дои:10.1063/1.3366241.
- Трейбер, Мартин; Кестинг, Арне; Хелбинг, Дирк (2010). «Теория трехфазного движения и двухфазные модели с фундаментальной схемой в свете стилизованных эмпирических фактов». Транспортные исследования, часть B: методологические. 44 (8–9): 983. arXiv:1004.5545. Bibcode:2010arXiv1004.5545T. CiteSeerX 10.1.1.186.2970. Дои:10.1016 / j.trb.2010.03.004.
- Хартенштейн, Ханнес (2010). «Теория транспортных потоков: три, а не две фазы» [обзор книги «Введение в современную теорию транспортных потоков и управление ими: долгий путь к трехфазной теории движения»; Kerner, B.S .; 2009)] ». Журнал IEEE Vehicular Technology Magazine. 5 (3): 91. Дои:10.1109 / MVT.2010.937837.