WikiDer > Транспортный поток
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
В математика и транспортная техника, транспортный поток представляет собой исследование взаимодействия между путешественниками (включая пешеходов, велосипедистов, водителей и их транспортные средства) и инфраструктурой (включая шоссе, указатели и устройства управления движением) с целью понимания и разработки оптимальной транспортной сети с эффективным движением движение и минимальный заторы на дорогах проблемы.
История
Попытки создать математическую теорию транспортных потоков относятся к 1920-м годам, когда Фрэнк Найт сначала провел анализ равновесия трафика, который был уточнен в Первый и второй принципы Уордропа равновесия в 1952 г.
Тем не менее, даже с появлением значительной вычислительной мощности компьютера, на сегодняшний день не существует удовлетворительной общей теории, которая могла бы быть последовательно применена к реальным условиям потока. ток модели движения использовать смесь эмпирический и теоретический техники. Эти модели затем развиваются в прогнозы движения, и принять во внимание предлагаемые местные или серьезные изменения, такие как увеличение использования транспортных средств, изменения в землепользование или изменения в вид транспорта (например, люди переходят от автобуса к поезду или машине), а также для определения областей скопление где сеть нужно настроить.
Обзор
Трафик ведет себя сложным и нелинейным образом, в зависимости от взаимодействия большого количества автомобили. Из-за индивидуальных реакций водителей-людей, транспортные средства не взаимодействуют просто по законам механики, а скорее отображают кластер. формирование и ударная волна распространение[нужна цитата] как вперед, так и назад, в зависимости от автомобиля плотность. Некоторые математические модели транспортного потока используют вертикальная очередь допущение, при котором транспортные средства, идущие по перегруженному звену, не возвращаются назад по его длине.
В свободной сети, теория транспортного потока относится к таким переменным, как скорость, поток и концентрация транспортного потока. Эти отношения в основном связаны с непрерывным транспортным потоком, в основном на автомагистралях или скоростных автомагистралях.[1] Условия потока считаются "свободными", если на дороге находится менее 12 автомобилей на милю на полосу движения. «Стабильный» иногда описывается как 12–30 автомобилей на милю на полосу движения. По достижении максимальной плотности массовый расход (или поток) и превышает оптимальную плотность (более 30 автомобилей на милю на полосу), транспортный поток становится нестабильным, и даже незначительное происшествие может привести к постоянному Остановись и иди условия вождения. Состояние «поломки» возникает, когда движение становится нестабильным и превышает 67 автомобилей на милю на полосу.[2] «Плотность пробок» относится к экстремальной плотности движения, когда транспортный поток полностью прекращается, обычно в диапазоне 185–250 автомобилей на милю на полосу.[3]
Однако расчеты перегруженных сетей более сложны и в большей степени основываются на эмпирических исследованиях и экстраполяциях фактических подсчетов дорог. Поскольку они часто бывают городскими или пригородными по своей природе, на оптимальные условия также влияют другие факторы (такие как безопасность участников дорожного движения и экологические соображения).
Существуют общие пространственно-временные эмпирические характеристики заторов, которые качественно одинаковы для разных автомагистралей в разных странах, измеренные в течение многих лет наблюдений за дорожным движением. Некоторые из этих общих черт перегруженности движения определяют синхронизированный поток и фазы движения с широкими движущимися заторами для перегруженного трафика в КернерС теория трехфазного движения транспортного потока (см. также Реконструкция пробок с помощью трехфазной теории Кернера).
Динамика одиночного автомобиля
Движение как функция времени
Позволять быть траекторией транспортного средства. Потом,
Или, что то же самое,
где всем переменным с индексом "0" заданы начальные условия в момент времени .
Движение как функция расстояния
В некоторых приложениях удобно использовать расстояние как независимую переменную. Траектория транспортного средства представлена , обратная функция .
- Если дано, можно получить как: .
- Если дано, можно получить с помощью цепного правила: , или . Это также можно записать как , или лучше как , которые можно интегрировать, чтобы получить . Следовательно,
Движение как функция скорости
Модели кинематики автомобиля дают «желаемое ускорение» что водитель навязывает транспортному средству при движении со скоростью вовремя в безнапорных условиях. Желаемая модель ускорения фиксирует как поведение водителя, так и физические ограничения, накладываемые геометрией проезжей части на двигатель.
Отмечая, что у нас есть , что в результате интегрирования дает . Позиция можно получить с помощью цепного правила:
Это дает и, следовательно
Модель линейного ускорения и безразмерная формулировка
Для легковых автомобилей хорошее приближение - это линейно убывающая функция скорости:
где имеет единицы и можно интерпретировать как желаемую скорость. Разумное типичное значение[4] из 0,06.
Безразмерные формулировки удобны тем, что уменьшают количество параметров, входящих в задачу. Определить, что означает, что мы измеряем время в единицах , а скорость в единицах . Количество
- это временной масштаб проблемы. Это означает, что время достижения системой равновесия от возмущения сравнимо с .
Соответствующее преобразование для пространственной переменной
получается заменой переменной с учетом того, что
Модель линейного ускорения теперь
с начальным условием . Настройка уравнения движения становятся
и единственный параметр - начальное условие .
Полностью беспараметрическая формулировка дается преобразованием
Модель ускорения становится с начальным условием ; это дает
Свойства потока трафика
Эта документация требует внимания специалиста по математике. (Июнь 2011 г.) |
Транспортный поток обычно ограничивается одномерным маршрутом (например, полосой движения). Пространственно-временная диаграмма графически показывает движение транспортных средств по пути во времени. Время отображается по горизонтальной оси, а расстояние - по вертикальной оси. Транспортный поток на пространственно-временной диаграмме представлен отдельными линиями траектории отдельных транспортных средств. Транспортные средства, следующие друг за другом по заданной полосе движения, будут иметь параллельные траектории, и траектории будут пересекаться, когда одно транспортное средство проезжает мимо другого. Временно-пространственные диаграммы являются полезными инструментами для отображения и анализа характеристик транспортного потока на данном участке дороги с течением времени (например, для анализа загруженности транспортного потока).
Существует три основных переменных для визуализации транспортного потока: скорость (v), плотность (обозначается k; количество транспортных средств на единицу пространства) и поток.[требуется разъяснение] (указано q; количество автомобилей в единицу времени).
Скорость
Скорость - это расстояние, пройденное за единицу времени. Невозможно отследить скорость каждого транспортного средства; Итак, на практике средняя скорость измеряется путем отбора проб транспортных средств в заданном районе за определенный период времени. Идентифицируются два определения средней скорости: «средняя скорость по времени» и «средняя космическая скорость».
- «Средняя скорость по времени» измеряется в контрольной точке на проезжей части за определенный период времени. На практике это измеряется с помощью петлевых детекторов. Детекторы петель, когда они распределены по контрольной области, могут идентифицировать каждое транспортное средство и отслеживать его скорость. Однако измерения средней скорости, полученные с помощью этого метода, неточны, потому что мгновенные значения скорости, усредненные для нескольких транспортных средств, не учитывают разницу во времени движения транспортных средств, которые движутся с разными скоростями на одном и том же расстоянии.[требуется разъяснение]
где м представляет количество транспортных средств, проезжающих фиксированную точку, и vя это скорость яй автомобиль.
- «Средняя космическая скорость» измеряется на всем отрезке дороги. Последовательные изображения или видео сегмента проезжей части позволяют отслеживать скорость отдельных транспортных средств, а затем рассчитывается средняя скорость. Считается более точным, чем средняя скорость по времени. Данные для космического расчета средней космической скорости могут быть взяты из спутниковых снимков, камеры или того и другого.
где п представляет количество транспортных средств, проезжающих по участку проезжей части.
Таким образом, "средняя космическая скорость" - это гармоническое среднее скоростей. Средняя по времени скорость никогда не меньше средней космической скорости: , где это дисперсия средней космической скорости[5]
На пространственно-временной диаграмме мгновенная скорость, v = dx / dt, транспортного средства равна наклону вдоль траектории транспортного средства. Средняя скорость транспортного средства равна наклону линии, соединяющей конечные точки траектории, где транспортное средство входит и покидает сегмент проезжей части. Вертикальное разделение (расстояние) между параллельными траекториями - это расстояние между ведущим и ведомым транспортным средством. Точно так же горизонтальное разделение (время) представляет собой движение транспортного средства (ч). Пространственно-временная диаграмма полезна для соотнесения длины пути и расстояния с потоком и плотностью движения соответственно.
Плотность
Плотность (k) определяется как количество транспортных средств на единицу длины проезжей части. В транспортном потоке двумя наиболее важными значениями плотности являются критическая плотность (kc) и плотности заедания (kj). Максимально достижимая плотность при свободном потоке составляет kc, в то время как kj максимальная плотность, достигаемая в условиях скопления. В целом плотность заедания в семь раз превышает критическую плотность. Плотность обратно пропорциональна расстоянию (ям), которое представляет собой межцентровое расстояние между двумя транспортными средствами.
Плотность (k) в пределах проезжей части (L) в данный момент (т1) равняется обратной величине среднего шага п транспортных средств.
На пространственно-временной диаграмме плотность может быть оценена в области A.
где тт общее время в пути А.
поток
Поток (q) - количество автомобилей, проезжающих контрольную точку за единицу времени, автомобилей в час. Обратный поток - это движение вперед (час), то есть время, которое проходит между яый автомобиль проезжает контрольную точку в пространстве и (я + 1) -й автомобиль. В заторе, час остается постоянным. Когда образуется пробка, час приближается к бесконечности.
Течение (q) прохождение неподвижной точки (Икс1) в интервале (Т) равно величине, обратной средней величине пути м транспортных средств.
На пространственно-временной диаграмме поток может быть оценен в области B.
где тд это общее расстояние, пройденное за B.
Обобщенная плотность и поток на пространственно-временной диаграмме
Более общее определение потока и плотности на пространственно-временной диаграмме проиллюстрировано областью C:
где:
Ударная волна скопления
В дополнение к предоставлению информации о скорости, потоке и плотности транспортных потоков, пространственно-временные диаграммы могут иллюстрировать распространение перегрузки вверх по потоку от узкого места трафика (ударная волна). Ударные волны перегрузки будут различаться по длине распространения в зависимости от восходящего потока трафика и плотности. Однако ударные волны обычно распространяются вверх по течению со скоростью примерно 20 км / ч.
Стационарный трафик
Движение на участке дороги называется стационарным, если наблюдатель не обнаруживает движения в произвольной области пространственно-временной диаграммы. Движение является стационарным, если все траектории транспортного средства параллельны и равноудалены. Он также является стационарным, если представляет собой суперпозицию семейств траекторий с этими свойствами (например, быстрые и медленные драйверы). Используя очень маленькое отверстие в шаблоне, можно иногда просматривать пустую область диаграммы, а иногда нет, так что даже в этих случаях можно сказать, что движение не было стационарным. Понятно, что при таком мелком уровне наблюдения стационарного движения не существует. Микроскопический уровень наблюдения должен быть исключен из определения, если трафик кажется похожим через большие окна. Фактически, мы еще больше ослабляем определение, требуя только, чтобы величины т (А) и d (А) быть примерно одинаковыми вне зависимости от того, где находится "большое" окно (А) размещен.
Методы анализа
Аналитики подходят к проблеме тремя основными способами, соответствующими трем основным шкалам наблюдения в физике:
- Микроскопическая шкала: На самом базовом уровне каждый автомобиль рассматривается как личность. Для каждого можно написать уравнение, обычно обыкновенное дифференциальное уравнение (ODE). Также можно использовать модели сотовой автоматизации, где дорога разделена на ячейки, каждая из которых содержит движущийся автомобиль или пуста. В Модель Нагеля – Шрекенберга простой пример такой модели. Когда автомобили взаимодействуют, он может моделировать коллективные явления, такие как пробки.
- Макроскопический масштаб: Аналогично моделям динамика жидкостей, считается полезным использовать систему уравнения в частных производных, которые балансируют законы для некоторых валовых количеств процентов; например, плотность транспортных средств или их средняя скорость.
- Мезоскопическая (кинетическая) шкала: Третья, промежуточная возможность - определить функцию который выражает вероятность наличия транспортного средства во время на позиции который бежит со скоростью . Эта функция, следуя методам статистическая механика, можно вычислить с помощью интегро-дифференциального уравнения, такого как Уравнение Больцмана.
Инженерный подход к анализу проблем транспортных потоков на автомагистралях в первую очередь основан на эмпирический анализ (т.е. наблюдение и математическая подгонка кривой). Одна из основных ссылок, используемых американскими проектировщиками, - это Руководство по пропускной способности шоссе,[6] опубликовано Совет по транспортным исследованиям, который является частью Национальная академия наук США. Это рекомендует моделировать потоки трафика, используя все время прохождения по каналу с использованием функции задержки / потока, включая эффекты постановки в очередь. Этот метод используется во многих моделях трафика в США и в модели SATURN в Европе.[7]
Во многих частях Европы используется гибридный эмпирический подход к планированию трафика, сочетающий макро-, микро- и мезоскопические характеристики. Вместо того, чтобы моделировать устойчивое состояние потока на поездку, моделируются переходные "пики спроса" или заторы. Они моделируются с использованием небольших «временных интервалов» в сети в течение рабочего дня или выходных. Обычно сначала оцениваются пункты отправления и назначения для поездок, и модель движения создается перед калибровкой путем сравнения математической модели с наблюдаемыми подсчетами фактических потоков движения, классифицированных по типам транспортных средств. Затем к модели применяется «матричная оценка» для достижения лучшего соответствия наблюдаемому количеству ссылок перед любыми изменениями, а пересмотренная модель используется для создания более реалистичного прогноза трафика для любой предложенной схемы. Модель будет запускаться несколько раз (включая текущий базовый уровень, прогноз «среднего дня», основанный на ряде экономических параметров и поддерживаемый анализом чувствительности), чтобы понять последствия временных блокировок или инцидентов в сети. На основе моделей можно просуммировать время, затраченное на работу всех водителей различных типов транспортных средств в сети, и таким образом определить средний расход топлива и выбросы.
Большая часть практики органов власти Великобритании, Скандинавии и Нидерландов заключается в использовании программы моделирования CONTRAM для крупных схем, которая разрабатывалась в течение нескольких десятилетий под эгидой Великобритании. Лаборатория транспортных исследований, а в последнее время при поддержке Шведское дорожное управление.[8] Моделируя прогнозы дорожной сети на несколько десятилетий в будущем, можно рассчитать экономические выгоды от изменений дорожной сети, используя оценки стоимости времени и других параметров. Результаты этих моделей можно затем использовать в программе анализа затрат и выгод.[9]
Кривые совокупного количества транспортных средств (N-кривые)
Было предложено, чтобы этот раздел был Трещина в новую статью под названием Кривая накопленного количества транспортных средств. (Обсудить) (Май 2020 г.) |
Кривая накопленного количества транспортных средств, N-кривая, показывает совокупное количество транспортных средств, проезжающих определенное место Икс по времени т, измеренный от проезда некоторого эталонного транспортного средства.[10] Эту кривую можно построить, если известно время прибытия отдельных транспортных средств, приближающихся к месту. Икс, а время отправления также известно, поскольку они отправляются с места Икс. Получение этого времени прибытия и отправления может включать сбор данных: например, можно установить два точечных датчика в местах. Икс1 и Икс2, и подсчитайте количество транспортных средств, которые проезжают этот сегмент, а также запишите время прибытия каждого транспортного средства в Икс1 и отходит от Икс2. Результирующий график представляет собой пару кумулятивных кривых, где вертикальная ось (N) представляет собой совокупное количество транспортных средств, которые проезжают две точки: Икс1 и Икс2, а горизонтальная ось (т) представляет собой время, прошедшее с Икс1 и Икс2.
Если транспортные средства не задерживаются при движении из Икс1 к Икс2, затем прибытие автомобилей на место Икс1 представлен кривой N1 и прибытие транспортных средств на место Икс2 представлен N2 на рисунке 8. Чаще кривая N1 известен как кривая прибытия транспортных средств на месте Икс1 и кривая N2 известен как кривая прибытия транспортных средств на месте Икс2. На примере однополосного сигнального подхода к перекрестку, где Икс1 расположение стоп-бара на подходе и Икс2 представляет собой произвольную линию на полосе приема, расположенную прямо напротив перекрестка, когда светофор зеленый, транспортные средства могут проехать через обе точки без задержки, а время, необходимое для прохождения этого расстояния, равно времени движения в свободном потоке. Графически это показано двумя отдельными кривыми на рисунке 8.
Однако, когда светофор красный, автомобили прибывают к полосе остановки (Икс1) и задерживаются на красный свет перед пересечением Икс2 через некоторое время после того, как сигнал станет зеленым. В результате у полосы остановки выстраивается очередь по мере того, как на перекресток прибывают новые автомобили, а светофор все еще остается красным. Таким образом, до тех пор, пока машина, прибывающая на перекресток, все еще находится в очереди, кривая N2 больше не представляет собой прибытие транспортных средств на место Икс2; теперь он представляет автомобили » виртуальное прибытие на месте Икс2, или другими словами, представляет собой прибытие автомобилей в Икс2 если они не задерживаются. Прибытие автомобилей на место Икс2, с учетом задержки от светофора, теперь представлена кривой N ′2 на рисунке 9.
Однако концепция виртуальная кривая прибытия ошибочен. Эта кривая неправильно показывает длину очереди, возникшую в результате прерывания движения (т. Е. Красный сигнал). Предполагается, что все автомобили все еще достигают стоп-бара, прежде чем их задержит красный свет. Другими словами, виртуальная кривая прибытия изображает штабелирование автомобилей вертикально у стоп-бара. Когда светофор становится зеленым, эти автомобили обслуживаются в порядке очереди (FIFO). Однако для многополосного подхода заказ на обслуживание не обязательно является FIFO. Тем не менее, интерпретация по-прежнему полезна из-за озабоченности по поводу средней общей задержки вместо общих задержек для отдельных транспортных средств.[11]
Ступенчатая функция против гладкой функции
На примере светофора N-кривые как гладкие функции. Однако теоретически построение графика N-кривые из собранных данных должны привести к ступенчатой функции (рисунок 10). Каждый шаг представляет собой прибытие или отправление одного транспортного средства в этот момент времени.[11] Когда N-кривая рисуется в более крупном масштабе, отражающем период времени, охватывающий несколько циклов, затем шаги для отдельных автомобилей можно игнорировать, и тогда кривая будет выглядеть как плавная функция (рисунок 8).
N-curve: характеристики транспортного потока
В N-curve может использоваться в ряде различных анализов трафика, включая узкие места на автострадах и динамическое назначение трафика. Это связано с тем, что ряд характеристик транспортного потока может быть получен из графика совокупных кривых подсчета транспортных средств. На рисунке 11 показаны различные характеристики транспортного потока, которые могут быть получены из N-кривые.
На рисунке 11 представлены различные характеристики транспортного потока:
| Символ | Определение |
|---|---|
| N1 | совокупное количество транспортных средств, прибывающих на место Икс1 |
| N2 | виртуальное совокупное количество транспортных средств, прибывающих на место Икс2, или совокупное количество транспортных средств, которые хотели бы пересечь Икс2 по времени т |
| N ′2 | фактическое совокупное количество транспортных средств, прибывающих на место Икс2 |
| TTFF | время, необходимое для поездки с места Икс1 к месту Икс2 в безнапорных условиях |
| ш(я) | задержка транспортного средства я как он путешествует из Икс1 к Икс2 |
| TT(я) | общее время, необходимое для поездки из Икс1 к Икс2 включая задержки (TTFF + ш(я)) |
| Q(т) | очередь в любое время т, или количество автомобилей, задерживаемых во время т |
| п | общее количество автомобилей в системе |
| м | общее количество задержанных автомобилей |
| TD | общая задержка, испытанная м транспортных средств (площадь между N2 и N ′2) |
| т1 | время, когда начинается скопление |
| т2 | время, когда перегрузка заканчивается |
На основе этих переменных средняя задержка, испытываемая каждым автомобилем, и средняя длина очереди в любой момент времени. т можно рассчитать, используя следующие формулы:
Гамильтон Якоби PDE
В зоне транспортного потока альтернативный способ решения кинематической волновой модели - рассматривать ее как Уравнение Гамильтона – Якоби, что особенно полезно при определении сохраняемых величин для механических систем.
Предположим, мы заинтересованы в нахождении кумулятивной кривой как функции времени и пространства, N (t, x). Основываясь на определении кумулятивной кривой, относится к потоку и относится к плотности. Обратите внимание, что соглашение о знаках должно быть согласованным. Тогда фундаментальная плотность потока () уравнение: может быть выражено в форме совокупного подсчета как:
- , где - известная граница.
Теперь для общей случайной точки на пространственно-временной диаграмме решение приведенного выше уравнения в частных производных эквивалентно решению следующей задачи оптимизации, которая минимизирует количество проезжающих транспортных средств:, где случайная точка на границе .
Функция определяется как максимальная скорость прохождения наблюдателей. В случае треугольной фундаментальная диаграмма, у нас есть . Скорость наблюдателя .Здесь обозначения соответствует емкости, соответствует критической плотности, и - скорость свободного потока и скорость волны соответственно.
С учетом сказанного, приведенная выше функция минимизации упрощается до: , где случайная точка на границе . Здесь мы ограничиваем обсуждение решения начальными задачами (IVP) и краевыми задачами (BVP).
Проблема начального значения
Проблема с начальным значением возникает, когда граничное условие задается в фиксированное время, например в и граница . Поскольку скорость наблюдателя ограничена , потенциальное решение ограничено двумя линиями и .
Таким образом, IVP определяется следующим образом:
Точка локального минимума возникает, когда производная первого порядка равна 0, а производная второго порядка больше 0. Или минимум происходит на границах. Итак, набор возможных решений выглядит следующим образом:
- это и
- и .
Решение будет минимально соответствующим всех кандидатских баллов. и все из условия 1).
В частности, если начальное условие - линейная функция,
Краевая задача
Точно так же краевая задача указывает, что граничное условие задано в фиксированном месте, например . Тем не менее, скорость наблюдателя ограничена . Для случайной точки , верхняя оценка кандидатов в решения: если , ; еще, .
BVP определяется следующим образом:
Производная первого порядка: всегда меньше 0, поскольку потоки не превышают пропускную способность. Таким образом, минимум происходит на верхней границе временной оси.
На практике люди используют этот метод для оценки состояния трафика на между двумя петлевыми детекторами, которые можно рассматривать как комбинацию двух краевых задач (одна на входе и одна на выходе). Обозначьте расположение петлевого детектора выше по потоку как и положение детектора контура ниже по потоку как . Основываясь на приведенном выше заключении, минимальное значение приходится на верхнюю границу по оси времени.
- , с участием
Приложения
Модель узкого места
Одно приложение N-curve - это модель узкого места, где кумулятивное количество транспортных средств известно в точке перед узкое место (т.е. это место Икс1). Однако общее количество транспортных средств на данный момент неизвестно. после узкое место (т.е. это место Икс2), а скорее только емкость узкого места или скорость разгрузки, μ, известен. Модель узких мест может быть применена к реальным ситуациям узких мест, например, возникающих в результате проблемы проектирования проезжей части или дорожного происшествия.
Возьмем участок проезжей части с узким местом, например, на рисунке 12. В каком-то месте Икс1 перед узким местом подъезжающие автомобили следуют регулярному N-кривая. Если узкое место отсутствует, скорость отправления автомобилей на месте Икс2 практически такая же, как и скорость прибытия на Икс1 в более позднее время (т.е. во время TTFF - безнапорный время в пути). Однако из-за узкого места система на месте Икс2 теперь может иметь скорость вылета только μ. При построении графика этого сценария мы, по сути, имеем ту же ситуацию, что и на рисунке 9, где кривая прибытия транспортных средств N1кривая вылета автомобилей без узкого места N2, а ограниченная кривая вылета автомобилей с учетом узкого места N ′2. Скорость разряда μ наклон кривой N ′2, и все те же характеристики транспортного потока, что и на рисунке 11, можно определить из этой диаграммы. Максимальную задержку и максимальную длину очереди можно найти в точке M на рисунке 13, где наклон N2 такой же, как наклон N ′2; т.е. когда виртуальная скорость прибытия равна скорости разгрузки / отправления μ.
В N-кривую в модели узкого места также можно использовать для расчета выгод от устранения узкого места, будь то с точки зрения увеличения пропускной способности или устранения инцидента на обочине проезжей части.
Тандемные очереди
Как было сказано в предыдущем разделе, N-кривая является применимой моделью для оценки задержки движения во времени путем установки совокупной кривой подсчета прибытия и отправления. Поскольку кривая может представлять различные характеристики движения и состояние дороги, ситуации задержки и очереди в этих условиях можно будет распознать и смоделировать с помощью N-кривых. Тандемные очереди возникают, когда между пунктами прибытия и отправления существует несколько узких мест. На рисунке 14 представлена качественная планировка участка проезжей части тандемной очереди с определенным начальным заездом. Узкие места вдоль ручья имеют свою пропускную способность ».μя [veh / time], а отправка определяется на нижнем конце всего сегмента.
Чтобы определить окончательный отъезд, D(т), это может быть доступный метод исследования отдельных отклонений, Dя(т). Как показано на рисунке 15, если пренебречь временем пробега свободного потока, отклонение BNя−1 будет виртуальный приезд Б.Н.я, который также можно представить как Dя−1(т) = Ая(т). Таким образом, N-образная кривая проезжей части с двумя узкими местами (минимальное количество BN вдоль проезжей части с тандемной очередью) может быть построена, как на рисунке 15, с μ1 < μ2. В этом случае D2(t) будет конечным выездом на эту проезжую часть с тандемной очередью 2-BN.
Относительно проезжей части тандемной очереди 3 БН с μ1 < μ2, если μ1 < μ2 < μ3, как и в случае 2-BN, D3(t) будет конечным выездом на эту проезжую часть с тандемной очередью 3-BN. Если, однако, μ1 < μ3 < μ2, D2Тогда (t) будет по-прежнему конечным выездом на проезжую часть тандемной очереди 3-BN. Таким образом, можно резюмировать, что устранение узкого места с минимальной мощностью будет окончательным отклонением всей системы, независимо от других возможностей и количества узких мест. На рисунке 16 показан общий случай с n BN.
Описанная выше модель N-образной кривой представляет собой важную характеристику тандемных систем очередей, заключающуюся в том, что окончательное отклонение зависит только от узкого места с минимальной пропускной способностью. С практической точки зрения, когда ресурсы (экономия, усилия и т. Д.) Инвестиций в системы тандемной очереди ограничены, вложения могут в основном сосредоточиться на узком месте с наихудшим состоянием.
Светофор
Сигнальный перекресток будет иметь особое поведение при выезде. Говоря упрощенно, постоянная пропускная способность свободного потока, μsсуществует во время зеленых фаз. Напротив, отпускающая способность во время красных фаз должна быть равна нулю. Таким образом, N-образная кривая вылета независимо от прибытия будет выглядеть, как на Рисунке 17 ниже: количество увеличивается с наклоном μs во время зеленого цвета и остаются такими же во время красного.
Насыщенный случай светофора возникает при полном использовании высвобождающей емкости. Этот случай обычно существует, когда поступающий спрос относительно велик. N-образное представление насыщенного случая показано на рисунке 18.
Ненасыщенный случай светофора возникает, когда высвобождение мощности используется не полностью. Этот случай обычно существует, когда поступающий спрос относительно невелик. Представление N-кривой ненасыщенного случая показано на рисунке 19. Если есть узкое место с пропускной способностью μб(<μs) ниже по потоку, окончательным отклонением системы "свет-узкое место" будет выходное узкое место.
Распределение динамического трафика
Распределение динамического трафика также можно решить с помощью N-кривая. Есть два основных подхода к решению этой проблемы: системный оптимум и пользовательское равновесие. Это приложение будет обсуждаться далее в следующем разделе.
Теория трехфазного трафика Кернера
Kerner’s теория трехфазного движения является альтернативной теорией транспортного потока. Вероятно, наиболее важным результатом трехфазной теории является то, что в любой момент времени существует диапазон пропускной способности магистрали свободного потока в узком месте. Диапазон производительности составляет от некоторой максимальной до минимальной производительности. Теория трехфазного движения противоречит фундаментальным классическим теориям движения, а также методам управления движением и управления движением, которые в любой момент времени предполагают наличие конкретный детерминированная или стохастическая пропускная способность магистрали свободного потока в узком месте.
Назначение трафика
Целью анализа транспортного потока является создание и реализация модели, которая позволила бы транспортным средствам добраться до места назначения в кратчайшие сроки, используя максимальную пропускную способность проезжей части. Это четырехэтапный процесс:
- Генерация - программа оценивает, сколько поездок будет сгенерировано. Для этого программе необходимы статистические данные о населенных пунктах, местонахождении рабочих мест и т. Д .;
- Распространение - после генерации он создает разные пары "источник-пункт назначения" (OD) между местоположением, найденным на шаге 1;
- Модальное разделение / выбор режима - система должна решить, какой процент населения будет разделен между различными видами доступного транспорта, например автомобили, автобусы, рельсы и т.д .;
- Назначение маршрута - наконец, маршруты назначаются транспортным средствам на основе правил минимальных критериев.
Этот цикл повторяется до схождения решения.
Есть два основных подхода к решению этой проблемы с конечными целями:
Оптимальная система
Короче говоря, сеть находится в системном оптимуме (SO), когда общая стоимость системы является минимальной среди всех возможных назначений.
Оптимальная система основана на предположении, что маршруты всех транспортных средств будут контролироваться системой, и что изменение маршрута будет основано на максимальном использовании ресурсов и минимальной общей стоимости системы. (Стоимость может быть интерпретирована как время в пути.) Следовательно, в алгоритме маршрутизации System Optimum все маршруты между заданной парой OD имеют одинаковые предельные затраты. В традиционной экономике транспорта оптимальная система определяется равновесием функции спроса и функции предельных затрат. . При таком подходе предельные издержки грубо изображаются как возрастающая функция в условиях загруженности дорог. В подходе, основанном на транспортных потоках, предельные затраты на поездку могут быть выражены как сумма затрат (время задержки, w), которые испытывает водитель, и внешних факторов (e), которые водитель накладывает на остальных пользователей.[12]
Предположим, есть автострада (0) и альтернативный маршрут (1), по которым пользователи могут выехать на съезд. Оператор знает общую скорость прибытия (A (t)), пропускную способность автострады (μ_0) и пропускную способность альтернативного маршрута (μ_1). С момента t_0, когда автострада перегружена, некоторые пользователи начинают переходить на альтернативный маршрут. Однако при "t_1" альтернативный маршрут также заполнен. Теперь оператор определяет количество автомобилей (N), которые будут использовать альтернативный маршрут. Оптимальное количество транспортных средств (N) может быть получено путем расчета вариации, чтобы сделать предельную стоимость каждого маршрута равной. Таким образом, оптимальным условием является T_0 = T_1 + ∆_1. На этом графике мы видим, что очередь на альтернативном маршруте должна очистить ∆_1 единиц времени, прежде чем она очистится от автострады. Это решение не определяет, как мы должны распределять транспортные средства, прибывающие между t_1 и T_1, мы просто можем сделать вывод, что оптимальное решение не является уникальным. Если оператор хочет, чтобы автострада не была перегружена, оператор может наложить плату за перегрузку, e_0-e_1, которая является разницей между внешним видом автострады и альтернативным маршрутом. В этой ситуации автострада будет поддерживать скорость свободного потока, однако альтернативный маршрут будет чрезвычайно загружен.
Пользовательское равновесие
Короче говоря, сеть находится в пользовательском равновесии (UE), когда каждый драйвер выбирает маршруты с наименьшими затратами между исходной точкой и пунктом назначения независимо от того, минимизирована ли общая стоимость системы.
Оптимальное равновесие для пользователей предполагает, что все пользователи выбирают свой собственный маршрут к месту назначения на основе времени в пути, которое будет затрачено на различные варианты маршрута. Пользователи выберут маршрут, требующий наименьшего времени в пути. Пользовательская оптимальная модель часто используется при моделировании влияния узких мест на шоссе на распределение трафика. Когда на шоссе возникает затор, увеличивается время задержки при движении по шоссе и увеличивается время в пути. В соответствии с оптимальным предположением пользователя, пользователи предпочтут подождать, пока время в пути по определенной автостраде не сравняется со временем в пути по городским улицам, и, следовательно, достигается равновесие. Это равновесие называется пользовательским равновесием, равновесием Уордропа или равновесием Нэша.
Основной принцип пользовательского равновесия заключается в том, что все используемые маршруты между данной парой OD имеют одинаковое время прохождения. Параметр альтернативного маршрута активируется, когда фактическое время в пути в системе достигает времени свободного движения по этому маршруту.
Для оптимальной модели пользователя шоссе, рассматривающей один альтернативный маршрут, типичный процесс распределения трафика показан на рисунке 15. Когда потребность в трафике остается ниже пропускной способности шоссе, время задержки на шоссе остается нулевым. Когда потребность в трафике превышает пропускную способность, на трассе появляется очередь автомобилей и время задержки увеличивается. Некоторые пользователи повернутся к городским улицам, когда время задержки достигнет разницы между временем свободного движения по шоссе и временем свободного движения по городским улицам. Это означает, что пользователи, оставшиеся на шоссе, потратят на дорогу столько же времени, сколько и те, кто свернут на городские улицы. На этом этапе время в пути как по шоссе, так и по альтернативному маршруту остается неизменным. Эта ситуация может закончиться, когда спрос упадет ниже пропускной способности дороги, то есть время в пути по шоссе начнет уменьшаться, и все пользователи останутся на шоссе. Сумма участков 1 и 3 представляет собой преимущества альтернативного маршрута.Сумма области 4 и области 2 показывает общую стоимость задержки в системе, в которой область 4 - это общая задержка, возникающая на шоссе, а область 2 - это дополнительная задержка из-за переключения движения на улицы города.
Функция навигации в Карты Гугл можно назвать типичным промышленным приложением динамического распределения трафика на основе пользовательского равновесия, поскольку оно предоставляет каждому пользователю вариант маршрутизации с наименьшими затратами (время в пути).
Временная задержка
И User Optimum, и System Optimum можно разделить на две категории на основе подхода к временной задержке, принятого для их решения:
Прогнозируемая временная задержка
Прогнозируемая временная задержка предполагает, что пользователь системы точно знает, как долго будет задержка. Прогнозирующая задержка знает, когда будет достигнут определенный уровень перегрузки и когда задержка этой системы будет больше, чем задержка другой системы, поэтому решение о перенаправлении может быть принято вовремя. На диаграмме количества транспортных средств прогнозируемая задержка в момент времени t представляет собой горизонтальный отрезок линии на правильно сторона времени t, между кривой прибытия и отправления, показанная на рисунке 16. соответствующая координата y - это номер n-го транспортного средства, которое уходит система в момент времени t.
Реактивное время задержки
Реактивная временная задержка - это когда пользователь не знает об условиях движения впереди. Пользователь ждет момента, когда наблюдается задержка, и решение о перенаправлении является реакцией на этот опыт в данный момент. Прогнозирующая задержка дает значительно лучшие результаты, чем метод реактивной задержки. На диаграмме количества транспортных средств и времени прогнозируемая задержка в момент времени t представляет собой горизонтальный отрезок линии на осталось сторона времени t, между кривой прибытия и отправления, показанная на рисунке 16. соответствующая координата y - это номер n-го транспортного средства, которое входит система в момент времени t.
Принцип Кернера минимизации сбоев сети (BM)
Кернер представил альтернативный подход к распределению трафика на основе своей сети принцип минимизации пробоев (BM). Вместо явной минимизации времени в пути, цель Оптимальная система и Пользовательское равновесие, принцип BM сводит к минимуму вероятность возникновения перегрузки в сети трафика.[13] При достаточном спросе на трафик применение принципа BM должно привести к неявной минимизации времени в пути в сети.
Назначение регулируемого ограничения скорости
Это предстоящий подход к устранению ударной волны и повышению безопасности транспортных средств. Концепция основана на том факте, что риск аварии на проезжей части увеличивается с увеличением разницы скоростей между движущимися вверх и вниз по потоку транспортными средствами. Два типа риска столкновения, которые могут быть уменьшены с помощью внедрения VSL, - это авария сзади и авария при смене полосы движения. Регулируемые ограничения скорости стремятся к равномерному распределению скорости, что приводит к более постоянному потоку.[14] Исследователи реализовали различные подходы к созданию подходящего алгоритма VSL.
Изменяемые ограничения скорости обычно применяются, когда датчики на проезжей части обнаруживают, что заторы или погодные явления превысили пороговые значения. Затем ограничение скорости на проезжей части будет уменьшено с шагом 5 миль в час за счет использования знаков над проезжей частью (динамические знаки сообщений), контролируемых Министерством транспорта. Целью этого процесса является как повышение безопасности за счет уменьшения количества аварий, так и предотвращение или отсрочка возникновения заторов на проезжей части. Идеальный результирующий транспортный поток в целом медленнее, но меньше остановок и остановок, что приводит к меньшему количеству аварий сзади и при смене полосы движения. При использовании VSL также регулярно используются плечевые полосы, разрешенные для перевозки только в густонаселенных штатах, на борьбу с которыми этот процесс направлен. Необходимость в ограничении переменной скорости показана справа на диаграмме плотности потока.
На этом рисунке («Диаграмма скорости потока для типичной проезжей части») точка кривой представляет оптимальное движение транспортного потока как по потоку, так и по скорости. Однако после этой точки скорость движения быстро достигает порогового значения и начинает быстро снижаться. Чтобы снизить потенциальный риск такого резкого снижения скорости, регулируемые ограничения скорости снижают скорость более плавно (с шагом 5 миль в час), позволяя водителям иметь больше времени для подготовки и адаптации к замедлению из-за заторов / Погода. Обеспечение постоянной скорости движения снижает вероятность неустойчивого поведения водителя и, следовательно, аварий.
На основе исторических данных, полученных на площадках VSL, было определено, что внедрение этой практики снижает количество аварий на 20-30%.[14]
Помимо вопросов безопасности и эффективности, VSL также может принести экологические выгоды, такие как снижение выбросов, шума и расхода топлива. Это связано с тем, что транспортные средства более экономичны при постоянной скорости движения, чем в состоянии постоянного ускорения и замедления, как это обычно бывает в условиях перегруженности.[15]
Ключевая теория фона
Фундаментальные отношения между объемом (q), скоростью (u) и плотностью (k) транспортного потока могут объяснить эффективность VSL. Взаимосвязь между этими переменными рассматривается в разделе «Свойства потока трафика» на этой странице, но в качестве важного вывода для целей объяснения VSL q = u * k. Упрощенная теория транспортного потока Ньюэлла также используется для этой модели, чтобы показать взаимосвязь, отображаемую на графике плотности потока, озаглавленном «Диаграмма идеальной плотности потока».[16]
Рисунок «Диаграмма идеальной плотности потока» показывает, что существует пиковая плотность, которую проезжая часть может выдержать в незагруженном состоянии, но если эта плотность будет превышена, то проезжая часть перейдет в состояние перегруженного движения. Эта плотность известна как критическая плотность или KC. Теория ударной волны используется в модели VSL для описания эффекта замедления потока из-за перегрузки. Ударные волны возникают на границе между двумя различными транспортными потоками, и их скорость может быть показана как отношение разности плотности к разнице объемов в двух состояниях движения.
VSL часто создает пустоту на пространственно-временной диаграмме в пространстве между траекторией транспортного средства при нормальной скорости и транспортным средством на пониженной скорости в пределах эффективных границ VSL. Ниже показаны две формы переменного ограничения скорости.
Начальный поток («qA»)> Перегруженный восходящий поток («qU») (случай 1)
Когда начальный поток на проезжей части больше, чем перегруженный поток вверх по потоку, за счет реализации VSL образуется ударная волна. Пространственно-временная диаграмма и плотность потока фундаментальная диаграмма (упрощенная до треугольной диаграммы) показаны справа. Эти диаграммы представляют состояние перегрузки. Обратите внимание, что хотя диаграммы не соответствуют друг другу, наклоны, представляющие скорость транспортного средства, одинаковы в каждом состоянии, одинаковы на обеих диаграммах.
Как видно на диаграммах случая 1, введение переменного ограничения скорости, когда начальный поток больше, чем перегруженный восходящий поток, приводит к пустоте в зоне VSL (состояние движения «O»). Зона VSL показана горизонтальными линиями. Нормальная скорость свободного потока u прерывается VSL, что приводит к новой скорости «v». Введение VSL приводит к возникновению ударной волны, как показано на обеих диаграммах. Реализация VSL также вводит новое состояние трафика «U» для скорости потока VSL (вместо «A» в начальных условиях) и новое состояние трафика «D» для нисходящих потоков. Состояния трафика «D» и «U» имеют одинаковую скорость потока, но с разной плотностью. Увеличение скорости обратно до «u» после зоны VSL приводит к снижению плотности в состоянии «D». Ударная волна, вызванная снижением скорости VSL, начинает воздействовать на проезжую часть с состоянием движения «U» после определенного времени активности. Это представляет собой возврат контролируемой задержки, установленной VSL. Состояние трафика «U» имеет более высокую плотность, но тот же поток, что и состояние «D», которое возникает после прохождения зоны VSL.
Перегруженный восходящий поток «(qU»)> Начальный поток («qA») (Случай 2)
Если перегруженный поток вверх по течению (обозначенный на следующих диаграммах как «U») больше, чем начальный поток на проезжей части вверх по течению («A»), то VSL поможет уменьшить количество остановок и движения, гомогенизируя поток движения, что приведет к состояние трафика «А» после его реализации. На диаграммах справа для случая 2 предположим, что все наклоны равны, несмотря на масштаб.
На диаграммах варианта 2 реализация VSL приводит к снижению скорости в указанной зоне. Однако в результате существующих состояний трафика с qU> qA трафик возвращается в исходное состояние «A» после зоны VSL. Расстояние между транспортными средствами «H» можно рассчитать между траекториями транспортных средств на пространственно-временной диаграмме или во время qA / v на основе плотности потока. фундаментальная диаграмма. В этой форме модели не формируется альтернативное состояние нисходящего трафика и не возникает ударная волна из-за перегрузки на VSL. Треугольник меньшего размера на диаграмме плотности потока представляет собой фундаментальную диаграмму для зоны VSL. В этой зоне транспортный поток нормализуется с более высокой плотностью, но более низким потоком, чем начальное условие «А» из-за пониженной скорости движения.
Теория VSL
При демонстрации эффективности VSL делается несколько ключевых предположений.
- На шоссе анализа нет пандусов въезда / выезда
- Анализ транспортного потока основан на траектории транспортного средства без ускорения / замедления.
- Учитываются только легковые автомобили
- Полное соответствие VSL от всех драйверов
- Сосредоточьтесь на уменьшении заторов
Определение эффективности VSL
Эффективность VSL может быть подтверждена количественно путем анализа ударных волн, образованных перегрузкой, с реализацией и без нее. В исследовании, цитируемом в этом разделе, для этого сравнения использовались ударные волны для инцидента вверх по течению. Одна ударная волна образовалась из-за перегрузки, вызванной инцидентом выше по течению, а другая - за счет очистки и восстановления этого инцидента, чтобы вернуться к нормальному потоку. Было установлено, что две ударные волны для системы с реализацией VSL привели к гораздо более короткой задержке и длине очереди из-за гомогенизации потока за счет более быстрого рассеивания первой ударной волны. В этом исследовании доказана эффективность VSL в снижении перегрузки, хотя и с ограничивающими предположениями, описанными выше.
Ограничения VSL
Реализация VSL наиболее идеальна в условиях сильной перегрузки. Если сокращенный VSL реализован в состояниях трафика с критической плотностью, это приведет к снижению общего потока за счет увеличения времени в пути. Таким образом, преимущества VSL должны быть реализованы с осторожностью только в пороговых состояниях, которые зависят от существующих данных трафика на проезжей части. Следовательно, датчики должны быть эффективно настроены, чтобы определять, когда начнется застойное состояние, на основе исторических данных. VSL также должен начинаться до того, как будут достигнуты постоянные перегруженные состояния трафика, чтобы быть эффективным.
Эффективность VSL также почти полностью зависит от соответствия драйверов. Этого можно добиться с помощью принудительного исполнения и динамических указателей. Водители должны понимать легитимность VSL, чтобы она была эффективной; причины нового ограничения скорости должны быть объяснены с помощью указателей, чтобы обеспечить соответствие. Если драйверы не считают VSL обязательным, он не будет работать эффективно. Если VSL уменьшится на значительную величину, соответствие значительно снизится. По этой причине большинство скоростей VSL на автострадах превышает 40 миль в час. Несколько исторических примеров показывают, что соответствие снижается гораздо быстрее, когда новое ограничение скорости падает ниже этого порога.
Системы VSL ограничены стоимостью детекторов и вывесок, которая может превышать 5 миллионов долларов. Сокращение задержек и аварий часто компенсирует первоначальные затраты на внедрение. Как правило, для эффективного установления VSL с соблюдением требований драйверов требуется 1-2 года. 17
Дорожные развязки
Большое внимание уделяется пропускной способности дороги при проектировании развязок. Допуская длинные «плетеные участки» на слегка изогнутых дорогах на неровных перекрестках, транспортные средства часто могут перемещаться по полосам, не создавая значительных помех для потока. Однако это дорого и занимает много земли, поэтому часто используются другие схемы, особенно в городских или очень сельских районах. Большинство больших моделей используют грубое моделирование перекрестков, но компьютерное моделирование доступно для моделирования определенных наборов светофоров, кольцевых развязок и других сценариев, когда поток прерывается или используется другими типами участников дорожного движения или пешеходов. Хорошо спроектированная развязка может обеспечить значительно больший транспортный поток при различной плотности движения в течение дня. Согласовав такую модель с «интеллектуальной транспортной системой», трафик может передаваться непрерывными «пакетами» транспортных средств с заданной скоростью через серию поэтапных светофоров. TRL разработала программы моделирования соединений для небольших местных схем, которые могут учитывать детальную геометрию и линии обзора; АРКАДИЯ для каруселей, ПИКАДИ для приоритетных перекрестков и OSCADY и TRANSYT для сигналов. Многие другие программные пакеты для анализа соединений[17] существуют такие как Сидра и LinSig и Synchro.
Кинематическая волновая модель
В кинематическая волна Впервые модель была применена к транспортному потоку Лайтхиллом и Уиземом в 1955 году. В их статье, состоящей из двух частей, впервые была разработана теория кинематических волн на примере движения воды. Во второй половине они распространили теорию на движение по «переполненным магистралям». Этот документ был в первую очередь посвящен развитию идеи «неровностей» (увеличения потока) и их влиянию на скорость, особенно через узкие места.[18]
Авторы начали с обсуждения предыдущих подходов к теории транспортных потоков. Они отмечают, что в то время проводилась некоторая экспериментальная работа, но что «теоретические подходы к предмету [находились] в зачаточном состоянии». В частности, один исследователь, Джон Глен Уордроп, в первую очередь интересовался статистическими методами исследования, такими как средняя космическая скорость, средняя скорость по времени, а также «влияние увеличения потока на обгон» и связанное с этим уменьшение скорости, которое это может вызвать. Другое предыдущее исследование было сосредоточено на двух отдельных моделях: одна связала скорость движения с потоком транспорта, а другая - скорость движения между транспортными средствами.[18]
С другой стороны, цель Лайтхилла и Уизема состояла в том, чтобы предложить новый метод исследования, «предложенный теориями потока о сверхзвуковых снарядах и движения паводка в реках». Результирующая модель будет отражать обе вышеупомянутые взаимосвязи, скорость-поток и скорость-движение, в единую кривую, которая «суммирует все свойства участка дороги, которые имеют отношение к его способности справляться с потоком перегруженный трафик ». Представленная ими модель соотносила транспортный поток с концентрацией (теперь обычно известной как плотность). Они писали: «Основная гипотеза теории состоит в том, что в любой точке дороги поток q (автомобилей в час) является функцией концентрации k (транспортных средств на милю)». Согласно этой модели, транспортный поток напоминал поток воды в том смысле, что «небольшие изменения потока распространяются обратно через поток транспортных средств вдоль« кинематических волн », скорость которых относительно дороги представляет собой наклон графика потока в зависимости от концентрации. ” Авторы включили пример такого графика; этот график зависимости расхода от концентрации (плотности) используется и сегодня (см. рисунок 3 выше).[18]
Авторы использовали эту модель концентрации потока, чтобы проиллюстрировать концепцию ударных волн, которые замедляют въезжающие в них транспортные средства, и условия, которые их окружают. Они также обсудили узкие места и пересечения, относящиеся как к их новой модели. Для каждой из этих тем были включены диаграммы концентрации потока и времени-пространства. Наконец, авторы отметили, что согласованного определения пропускной способности не существует, и утверждали, что ее следует определять как «максимальный поток, на который способна дорога». Лайтхилл и Уизем также признали, что их модель имеет существенное ограничение: она подходит только для использования на длинных, многолюдных дорогах, поскольку подход «непрерывного потока» работает только с большим количеством транспортных средств.[18]
Компоненты кинематической волновой модели теории транспортных потоков
Кинематическая волновая модель теории транспортного потока - это простейшая динамическая модель транспортного потока, воспроизводящая распространение волны движения. Он состоит из трех компонентов: фундаментальная диаграмма, уравнение сохранения и начальные условия. Закон сохранения - это фундаментальный закон, регулирующий кинематическую волновую модель:
Принципиальная схема кинематической волновой модели связывает транспортный поток с плотностью, как показано на рисунке 3 выше. Это можно записать так:
Наконец, необходимо определить начальные условия для решения проблемы с использованием модели. Граница определяется как , представляющий плотность как функцию времени и положения. Эти границы обычно принимают две разные формы, что приводит к проблемам начального значения (IVP) и краевым проблемам (BVP). Задачи с начальным значением дают плотность трафика во время , так что , где - заданная функция плотности. Краевые задачи дают некоторую функцию что представляет собой плотность на положение, такое что . Модель имеет множество применений в транспортном потоке. Одно из основных применений - моделирование узких мест трафика, как описано в следующем разделе.
Транспортное уравнение
Предполагая постоянную скорость волны, , то кинематическая волна Модель можно иначе назвать уравнением переноса, которое является ключевым строительным блоком для более упрощенного решения KW.
Проблема начального значения
Во-первых, рассмотрим проблема начального значения (IVP), то есть , для уравнения переноса:
k, таким образом, можно решить как . Это называется Раствор IVP. Это означает, что вдоль линий с одинаковым наклоном w на пространственно-временной диаграмме плотность k постоянна. Эти строки называются характеристики. Более конкретно:
Краевая задача
Рассмотрим Краевая задача (BVP), то есть , для уравнения переноса:
k, таким образом, можно решить как . Это называется BVP решение. Подобно решению IVP, это означает, что вдоль линий с одинаковым наклоном w на пространственно-временной диаграмме, или так называемых характеристики, плотность k остается постоянной.
Предполагается, что, когда начальные условия кусочно-постоянные, скорость волны каждого куска также постоянна, поэтому уравнение переноса выполняется.
Проблема Римана
В Проблема Римана обеспечивает основу для разработки численных решений кинематической волновой модели. Рассмотрим начальные значения:
Случай 1:
Это процесс замедления, когда трафик меняется со скоростью волны к , а плотность от к . Замедление приводит к прерывистости дорожного движения и возникновению "ударной волны":
Эффект ударной волны показан на Рисунке 17. Состояние движения меняется от U (свободный поток) к D (перегруженный). Наклон s этой ударной волны на пространственно-временной диаграмме представлен прямой линией, соединяющей точки U и D.
Случай 2:
Это процесс ускорения, когда трафик идет от скорости волны к , а плотность от к . Наклон s этой ударной волны может быть таким же, как в случае 1, но это решение не является уникальным, и состояние трафика не возвращается обратно по прямой от точки D к U. Трафик восстанавливается вдоль кривой фундаментальной диаграммы, а не возвращается в скорость свободного потока сразу. Это приводит к множеству различных «ударных волн решения», исходящих от заданного x0. Эти механизмы показаны на рисунке 18.
В этом случае часто условие энтропии (EC) используется для выбора единственного решения. EC находит решение, которое максимизирует поток в каждом месте, используя метод исчезающей вязкости.
Модели слияния Newell-Daganzo
В условиях, когда транспортные потоки выходят из двух ответвлений проезжей части и сливаются в единый поток через одну проезжую часть, определение потоков, которые проходят через процесс объединения, и состояния каждой ответвления дорог становится важной задачей для инженеров-транспортников. Модель слияния Ньюэлла-Даганзо - хороший подход для решения этих проблем. Эта простая модель является результатом описания Гордоном Ньюэллом процесса слияния.[19] и Даганзо модель передачи ячеек.[20] Чтобы применить модель для определения потоков, которые выходят из двух ветвей дорог, и состояния каждой ветки дорог, необходимо знать пропускную способность двух входных ветвей дорог, выходную пропускную способность, потребности для каждой ветки дорог. , и количество полос проезжей части. Коэффициент объединения будет рассчитан для определения доли двух входных потоков, когда обе ветви дороги работают в условиях перегруженности.
Как видно на упрощенной модели процесса слияния,[21] выходная пропускная способность системы определяется как μ, пропускная способность двух входных ветвей дорог определяется как μ1 и μ2, а потребности для каждой ветви дорог определены как q1D и q2D. Q1 и q2 являются выходными данными модели, которые представляют собой потоки, проходящие через процесс слияния. Процесс модели основан на предположении, что сумма пропускных способностей двух входных ветвей дорог меньше, чем выходная пропускная способность системы μ1+ μ2 ≤ μ.
Решение для модели слияния Newell-Daganzo
Потоки, проходящие через процесс слияния, q1 и q2, определяются приоритетом разделения или коэффициентом объединения. Состояние каждой ветви автомобильных дорог определяется графически с вводом заявок на каждую ветку автомобильных дорог, q1D и q2D. Система слияния может иметь четыре возможных состояния: оба впускных канала в режиме свободного потока, один из входных отверстий в состоянии перегрузки и оба входа находятся в состоянии перегрузки.
Обычный подход к вычислению коэффициента объединения p называется «правилом застежки-молнии», при котором p рассчитывается на основе количества полос на одной проезжей части, когда оба входа находятся в заторе. Если на одной проезжей части n полос, то по правилу застежки-молнии p = 1 / (2n-1). Этот коэффициент объединения также является отношением минимальных пропускных способностей входов μ1* и μ2*. μ1* + μ2* = μ. В результате q1= (μ1*/ μ) * μ и q2= (μ2*/ μ) * μ.
Состояние каждой ветки проезжей части определяется графическим решением, которое показано справа. По оси абсцисс отложено возможное значение q1 а по оси ординат - возможное значение q2Возможная область требований определяется максимально возможными значениями q1D и q2D которые являются μ1 и μ2. В возможный регион для q1 и q2 определяется как пересечение линии q1 + q2 = μ и возможный регион требований. Коэффициент слияния p откладывается от начала координат до линии q1 + q2 = μ.
Четыре возможных состояния системы слияния показаны на графике областями, отмеченными A1, A2, A3 и A4. Конкретные состояния системы слияния определяются областью, в которую попадают входные данные. Область A1 представляет состояние, когда и вход 1, и вход 2 находятся в свободном потоке. Область A2 представляет состояние, когда входное отверстие 1 находится в свободном потоке, а входное отверстие 2 находится в состоянии перегрузки. Область A3 представляет состояние, когда вход 1 находится в состоянии перегрузки, а вход 2 находится в свободном потоке. Область A4 представляет состояние, когда и вход 1, и вход 2 находятся в перегрузке.
Узкое место трафика
Узкие места движения - это нарушения движения на проезжей части, вызванные либо конструкцией дороги, светофором, либо авариями. Есть два основных типа узких мест: стационарные и подвижные. Стационарные узкие места - это те, которые возникают из-за нарушения, возникающего из-за стационарной ситуации, такой как сужение проезжей части или аварии. С другой стороны, движущиеся узкие места - это те транспортные средства или поведение транспортных средств, которые вызывают нарушения в транспортных средствах, движущихся впереди транспортного средства. Как правило, движущиеся узкие места возникают из-за тяжелых грузовиков, поскольку они являются медленно движущимися автомобилями с меньшим ускорением и также могут менять полосу движения.
Узкие места являются важными факторами, поскольку они влияют на поток транспорта и среднюю скорость транспортных средств. Основное последствие возникновения узкого места - немедленное снижение пропускной способности проезжей части. Федеральное управление автомобильных дорог заявило, что 40% всех заторов возникает из-за узких мест. На рисунке 16 показана круговая диаграмма для различных причин заторов. Рисунок 17[22] показывает общие причины скопления или узких мест.
Стационарное узкое место
Общей причиной стационарных узких мест является падение с полосы движения, которое происходит, когда многополосная дорога теряет одну или несколько полос. Это приводит к слиянию автомобильного движения на конечных полосах движения с другими полосами движения.
Представьте себе участок шоссе с двумя полосами движения в одном направлении. Предположим, что фундаментальная диаграмма моделируется, как показано здесь. Пиковая пропускная способность автострады составляет Q автомобилей в час, что соответствует плотности k.c автомобилей на милю. Трасса обычно забита на kj автомобилей на милю.
До того, как будет достигнута пропускная способность, трафик может идти со скоростью A автомобилей в час или более высокой скоростью B автомобилей в час. В любом случае скорость транспортных средств равна vж, или «свободный поток», потому что проезжая часть не имеет пропускной способности.
Теперь предположим, что в некотором месте x0, шоссе сужается до одной полосы движения. Максимальная вместимость теперь ограничена D 'или половиной Q, поскольку доступна только одна дорожка из двух. D имеет ту же скорость потока, что и состояние D ', но его транспортная плотность выше.
Используя пространственно-временную диаграмму, мы можем смоделировать событие узкого места. Предположим, что в момент времени 0 трафик начинает движение со скоростью B и скоростью vж. По истечении времени t1 транспортные средства прибывают с меньшим расходом A.
Прежде, чем первые машины достигнут точки x0, транспортный поток беспрепятственный. Однако после x0, проезжая часть сужается, уменьшая пропускную способность вдвое - и ниже, чем в состоянии B. Из-за этого транспортные средства начнут стоять в очереди перед x0. Это представлено состоянием высокой плотности D. Скорость автомобиля в этом состоянии меньше v.d, как взято из фундаментальной диаграммы. После узкого места транспортные средства переходят в состояние D ', где они снова движутся со скоростью свободного потока vж.
Как только машины прибудут со скоростью A, начиная с момента t1, очередь начнет очищаться и в конечном итоге исчезнет. Состояние A имеет скорость потока ниже пропускной способности одной полосы состояний D и D '.
На пространственно-временной диаграмме примерная траектория транспортного средства представлена пунктирной стрелкой. Диаграмма может легко представить задержку транспортного средства и длину очереди. Достаточно просто провести горизонтальные и вертикальные измерения в области состояния D.
Перемещение узкого места
Как объяснялось выше, движущиеся узкие места возникают из-за медленно движущихся транспортных средств, которые вызывают нарушение движения. Движущиеся узкие места могут быть активными или неактивными. Если приведенная емкость (qты), вызванное движущимся узким местом, превышает фактическую пропускную способность (μ) на выходе из транспортного средства, то это узкое место считается активным узким местом. На рисунке 20 показан случай, когда грузовик движется со скоростью «v» и приближается к месту ниже по потоку с грузоподъемностью «μ». Если уменьшенная грузоподъемность грузовика (qты) меньше, чем мощность на выходе, то грузовик становится неактивным узким местом.
Laval 2009, представляет основу для оценки аналитических выражений для сокращения пропускной способности, вызванного подмножеством транспортных средств, вынужденных замедляться на горизонтальных / вертикальных кривых на многополосной автостраде. На каждой полосе неэффективный поток описывается с точки зрения его желаемого распределения скорости и моделируется согласно кинематической волновой теории Ньюэлла для движущихся узких мест. Смена полосы движения при наличии грузовиков может положительно или отрицательно сказаться на пропускной способности. Если целевая полоса пуста, смена полосы увеличивает пропускную способность.
В этом примере рассмотрим три полосы движения в одном направлении. Предположим, грузовик начинает движение со скоростью v, меньшей скорости свободного потока vж. Как показано на фундаментальная диаграмма ниже qты представляет собой уменьшенную пропускную способность (2/3 Q или 2 из 3 имеющихся полос) вокруг грузовика.
Состояние A представляет собой нормальный приближающийся транспортный поток, снова на скорости v.ж. Состояние U, с расходом qты, соответствует очереди перед грузовиком. На основной диаграмме скорость автомобиля vты медленнее, чем vж. Но как только водители объезжают грузовик, они могут снова ускориться и перейти в состояние D вниз по потоку. В то время как это состояние движется со свободным потоком, плотность транспортных средств меньше, поскольку меньшее количество транспортных средств преодолевает узкое место.
Предположим, что в момент времени t грузовик замедляется от свободного движения до v. За грузовиком выстраивается очередь, представленная состоянием U. В области состояния U транспортные средства движутся медленнее, как показано на примере траектории. Поскольку состояние U ограничивается меньшим потоком, чем состояние A, очередь возвращается за грузовиком и в конечном итоге вытесняет всю трассу (уклон s отрицательный). Если бы у состояния U был более высокий поток, все равно была бы растущая очередь. Однако он не сможет вернуться назад, потому что наклон s будет положительным.
Проблема Римана
Представьте себе сценарий, в котором дорога с двумя полосами движения превращается в одну полосу движения в точке. Иксо отсюда пропускная способность дороги снижается до половины от первоначальной (½µ), Случай I. Позже по дороге в точке Икс1 2-я полоса открывается, и емкость восстанавливается до исходной (µ), Случай II.
- Случай I
Существует узкое место, ограничивающее поток транспорта, что приводит к увеличению плотности автомобилей (k) в месте (Иксо). Это приводит к замедлению всех встречных автомобилей, движущихся со скоростью u, до замедления до скорости. vd. Эта ударная волна будет распространяться со скоростью наклона линии U-D на фундаментальной диаграмме. Скорость волны можно рассчитать как vшок = (qD − qU)/(kD−kU). Эта линия отделяет трафик с перегрузкой от встречного свободного движения. Если наклон U-D на фундаментальной диаграмме положительный, затор продолжится вниз по течению от шоссе. Если он имеет отрицательный наклон, затор продолжится вверх по течению (см. Рисунок а[22]). Это замедление является случаем I задачи Римана (см. Рисунки b и c).
- Дело II
В случае II проблемы Римана движение переходит от заторов к свободному потоку, и автомобили ускоряются по мере снижения плотности. Опять же, наклон этих ударных волн можно рассчитать по той же формуле vшок = (qD − qU)/(kD−kU). На этот раз разница заключается в том, что транспортный поток движется по основной диаграмме не по прямой линии, а по множеству уклонов между различными точками изогнутой основной диаграммы (см. Рисунок d). Это вызывает множество линий, исходящих из точки Икс1 все в форме веера, называемой разрежением (см. рисунок е). Эта модель подразумевает, что позже пользователям потребуется больше времени для ускорения, когда они встретятся с каждой из линий. Вместо этого лучшим приближением является треугольная диаграмма, на которой движение резко увеличивается, как если бы водитель увидел перед собой проход (см. Рисунки f и g).
Критика
В критическом обзоре[23] Кернер объяснил, что общепринятые классические основы и методики теории дорожного движения и транспорта несовместимы с набором фундаментальных эмпирических характеристик распределения трафика на узких местах шоссе.
Набор фундаментальных эмпирических характеристик распределения трафика на узких местах шоссе
Набор фундаментальных эмпирических характеристик распределения трафика на узком месте шоссе выглядит следующим образом:
- Нарушение движения на узком месте автомагистрали - это локальный фазовый переход от свободного (F) для перегруженного трафика, входящий фронт которого обычно фиксируется в узком месте. Такой перегруженный трафик называется синхронизированным потоком (S). В нижнем фронте синхронизированного потока транспортные средства ускоряются от синхронизированного потока перед узким местом до свободного потока за узким местом.
- В то же время нарушение трафика может быть спонтанным или вынужденным.
- Вероятность нарушения трафика - это возрастающая функция расхода.
- Существует хорошо известное явление гистерезиса, связанное с перебоями в потоке: когда пробой произошел при некоторых скоростях потока, что привело к формированию перегруженной структуры перед узким местом, то возвратный переход к свободному потоку в узком месте обычно наблюдается при значительно меньших расходах. .
Происходит самопроизвольный сбой трафика, когда есть свободные потоки как вверх, так и вниз по потоку от узкого места до того, как произойдет сбой. Напротив, вызванный сбой трафика вызван распространением схемы перегруженности, которая возникла ранее, например, в другом узком месте ниже по потоку.
Эмпирические данные, которые иллюстрируют набор фундаментальных эмпирических характеристик распределения трафика в узких местах на автомагистралях, а также объяснения эмпирических данных можно найти в статье Википедии. Принцип минимизации поломки Кернера и в обзоре.[23]
Классические теории транспортных потоков
Общепринятыми классическими основами и методологиями теории дорожного движения и транспорта являются:
- Модель Лайтхилла-Уизема-Ричардса (LWR), представленная в 1955–56 гг.[18][24] Даганзо представил модель передачи клеток (CTM), которая согласуется с моделью LWR.[25]
- Неустойчивость транспортного потока, вызывающая нарастающую волну локального снижения скорости транспортного средства. Эта классическая нестабильность транспортного потока была введена в 1959–61 в модели следования за автомобилем General Motors (GM) Германом, Газисом, Монтроллом, Поттсом и Ротери.[26][27] Классическая нестабильность транспортного потока модели GM была включена в огромное количество моделей транспортных потоков, таких как модель Гиппса, модель Пейна, модель оптимальной скорости Ньюэлла (OV), модель Видемана, модель Уизема, клеточный автомат Нагеля-Шрекенберга (NaSch). (CA) модель, Bando et al. Модель OV, IDM Трейбера, модель Краусса, модель Aw-Rascle и многие другие хорошо известные микроскопические и макроскопические модели транспортных потоков, которые являются основой моделирование движения инструменты, широко используемые инженерами и исследователями трафика (см., например, ссылки в обзоре[23]).
- Понимание пропускной способности магистрали как конкретный ценность. Такое понимание пропускной способности дорог, вероятно, появилось в 1920–1935 гг. (См. [28]). В настоящее время предполагается, что пропускная способность автострады в свободном потоке в узком месте автострады является стохастической величиной. Однако в соответствии с классическим пониманием пропускной способности автострады предполагается, что в данный момент времени может быть только одно конкретное значение этой стохастической пропускной способности автострады (см. Ссылки в книге[29]).
- Принципы пользовательского равновесия (UE) и системного оптимума (SO) Wardrop для оптимизации и контроля трафика и транспортной сети.[30]
Несостоятельность классических теорий транспортных потоков
Кернер объясняет несостоятельность общепринятых классических теорий транспортных потоков следующим образом:[23]
- Теория LWR терпит неудачу, потому что эта теория не может показать эмпирические нарушения трафика, наблюдаемые в реальном движении. Соответственно, все приложения теории LWR к описанию распределения трафика в узких местах на автомагистралях (например, связанные приложения модели передачи ячеек Даганзо, кривые совокупного количества транспортных средств (N-кривые), модель узких мест, модели пропускной способности шоссе, а также связанные с ними приложения кинематической волновой теории) также несовместимы с набором фундаментальных эмпирических характеристик распределения трафика.
- Двухфазные модели транспортных потоков класса GM-моделей (см. Ссылки в[23]) терпят неудачу, поскольку обрыв трафика в моделях класса GM является фазовым переходом от свободного потока (F) к движущейся пробке (J) (называемый переходом F → J): в модели транспортного потока, принадлежащей классу моделей GM, из-за разбивки трафика движущиеся пробки возникают спонтанно в изначально свободном потоке в узком месте на шоссе. В отличие от этого результата модели, реальный сбой трафика - это фазовый переход от свободного потока (F) в синхронизированный поток (S) (так называемый переход F → S): вместо движущихся заторов из-за перебоев в реальном трафике возникает синхронизированный поток, нижний фронт которого фиксируется в узком месте.
- Понимание пропускной способности автодороги как особой величины (см. Ссылки в книге [29]) не работает, поскольку это предположение о характере пропускной способности шоссе противоречит эмпирическим свидетельствам того, что нарушение дорожного движения может быть вызвано узким местом на шоссе.
- Динамическое назначение трафика и / или любые виды оптимизации и управления трафиком, основанные на принципах SO или UE Wardrop, не работают из-за возможных случайных переходов между свободным потоком и синхронизированным потоком в узких местах магистрали. Из-за таких случайных переходов минимизация стоимости проезда в транспортной сети невозможна.
По словам Кернера,[23] Несоответствие общепринятых классических основ и методологий теории дорожного движения и транспорта с набором фундаментальных эмпирических характеристик распределения трафика в узких местах на автомагистралях может объяснить, почему подходы к оптимизации и контролю сети, основанные на этих основах и методологиях, потерпели неудачу при их применении в реальных условиях. Мир. Даже несколько десятилетий очень интенсивных усилий по улучшению и проверке моделей оптимизации сети не увенчались успехом. В самом деле, не существует примеров, когда онлайн-реализации моделей оптимизации сети, основанные на этих основах и методологиях, могли бы уменьшить перегрузку в реальных сетях трафика и транспортных сетях.
Это связано с тем, что фундаментальные эмпирические особенности распределения трафика на узких местах автомагистралей были изучены только в течение последних 20 лет. Напротив, общепринятые основы и методики теории дорожного движения и транспорта были внедрены в 50-60-е годы. Таким образом, ученые, идеи которых привели к этим классическим основам и методологиям теории дорожного движения и транспорта, не могли знать набор эмпирических характеристик реальной структуры дорожного движения.
Несоизмеримость теории трехфазного движения Кернера и классических теорий транспортного потока
Объяснение пробоя трафика в узком месте на шоссе переходом F → S в метастабильный свободный поток в узком месте является основным предположением Кернера. теория трехфазного движения.[23] Теория трехфазного трафика согласуется с набором фундаментальных эмпирических характеристик распределения трафика.Никто из более ранних теорий транспортного потока включает переход F → S в метастабильный свободный поток в узком месте. Следовательно, как упоминалось выше, ни одна из классических теорий транспортных потоков не согласуется с набором эмпирических характеристик реальной структуры трафика в узких местах шоссе. Фазовый переход F → S в метастабильном свободном потоке в узком месте магистрали действительно объясняет эмпирические свидетельства индуцированного перехода от свободного потока к синхронизированному потоку вместе с зависимостью вероятности разрушения от расхода. Согласно классической книге Куна,[31] это показывает несоизмеримость трехфазной теории и классических теорий транспортных потоков (подробнее см. [32]):
Минимальная пропускная способность магистрали , при котором фазовый переход F → S все еще может быть вызван в узком месте на шоссе, как указано в теории Кернера, имеет нет смысл других теорий и моделей транспортных потоков.
Период, термин "несоизмеримость" был введен Куном в его классической книге[31] объяснить смена парадигмы в научной сфере. Наличие этих двух фаз движения, свободный поток (F) и синхронизированный поток (S) при той же скорости потока не является следствием стохастического характера движения: даже если в движении транспортных средств не было стохастических процессов, состояния F и S существуют с той же скоростью потока. Однако классические стохастические подходы к управлению трафиком не предполагают возможность фазового перехода F → S в метастабильном свободном потоке. По этой причине эти стохастические подходы не могут решить проблему несовместимости классических теорий с набором эмпирических характеристик реальной структуры трафика.
Автомобильные модели
Модели слежения за автомобилем описывают, как одно транспортное средство следует за другим в непрерывном транспортном потоке.
Введение в три представления транспортного потока
Существует три представления транспортного потока, все эти три представления соответствуют одной и той же поверхности в трехмерном пространстве номера транспортного средства, положения и времени:
- N(т,Икс): количество транспортных средств, пересекших локацию Икс к тому времени т, представленные в эйлеровых координатах (т,Икс).
- Икс(т,п): положение автомобиля п в это время т, представленные в лагранжевых координатах (т,п).
- Т(п,Икс): время автомобиля п пересекает позицию Икс, представленные в лагранжевых координатах (п,Икс).
На основе теории Уравнение Гамильтона-Якоби вышеупомянутые решения (Хопф-Лакс формулу) трех моделей можно представить в виде:
Для N(т,Икс) модель Гамильтона-Якоби в частных производных основана на фундаментальной диаграмме плотности потока, функция Лагранжа может быть представлена как , в случае фундаментальной диаграммы траншеи , скорость волны, критическая плотность, это емкость. Икс(т,п) модель Гамильтона-Якоби в частных производных основана на фундаментальной диаграмме разнесения-скорости, функция Лагранжа может быть представлена как , в случае фундаментальной диаграммы траншеи , это волновой поток, критический интервал, - скорость свободного потока. Т(п,Икс) модель Гамильтона-Якоби в частных производных основана на фундаментальной диаграмме темп-прогресс, функция Лагранжа может быть представлена как , в случае фундаментальной диаграммы траншеи , расстояние между волнами, скорость свободного потока, это емкость.
Обратите внимание, что каждой модели описано в таблице ниже:
| Проблема начального значения | Краевая задача | |
|---|---|---|
| : совокупный профиль автомобиля в | : совокупная кривая cout при | |
| : положение автомобиля п в | : траектория ведущего автомобиля | |
| : траектория ведущего автомобиля | : время для автомобиля п выехать на участок дороги |
X-модели
Рассматривая треугольную фундаментальную диаграмму плотности потока, мы можем получить и , и соответственно модель слежения за автомобилем может быть описана через модель:
где - это расстояние между транспортными средствами, и расстояние между бампером и бампером, при котором происходит заклинивание транспортных средств, можно получить как . Решение может быть графически показано на рисунках 28 и 29.
Когда применяется постоянный интервал, исходные данные являются линейными, и модель следования за автомобилем может быть упрощена до:
Тогда, если мы разделим пространственно-временную плоскость на сетки , и мы интерпретируем начало координат (0,0) как , общая следующая модель автомобиля становится:
Решение можно интуитивно интерпретировать на пространственно-временной диаграмме на рисунке 30: траектория транспортного средства п - нижняя граница между (i) траекторией движения ведущего транспортного средства по характеристикам уклона , и (ii) собственная траектория в условиях свободного потока.
Однако обычная модель следования за автомобилем предполагает бесконечное ускорение транспортного средства, что непрактично. Чтобы компенсировать этот недостаток, мы можем включить модель кинематики транспортного средства в модель слежения за автомобилем. Кинематику транспортного средства можно выразить в виде модели линейного ускорения:
в котором - коэффициент ускорения, желаемая скорость.
Определить как результирующее смещение во времени для автомобиля начиная со скоростью в момент времени 0 следующая модель обычного автомобиля с границами ускорения будет:
Примеры моделей, следующих за автомобилем
Модель следования за автомобилем Ньюэлла
Вспомните общую модель следования за автомобилем, которую мы получаем из X-модели выше, модель следования за автомобилем Ньюэлла может быть получена с помощью настройки и :
в котором представляет траекторию движения транспортного средства в условиях свободного потока, а - траектория движения транспортного средства в условиях загруженности.
Некоторые дополнительные объяснения и примеры можно найти на веб-странице Википедии. Модель следования за автомобилем Ньюэлла.
Модель труб
Луи А. Пайпс начал исследования и получил признание общественности в начале 1950-х годов. Трубы автомобильные модели [33] основан на правилах безопасного вождения в Калифорнийский кодекс транспортных средств, и в этой модели использовалось предположение о безопасном расстоянии: хорошее правило для следования за другим транспортным средством состоит в том, чтобы выделить расстояние между транспортными средствами, равное по крайней мере длине автомобиля, на каждые десять миль в час скорости транспортного средства. Математически безопасное расстояние в модели Pipes, следующей за автомобилем, может быть получено как:
в котором расстояние между автомобилями и предшествующий автомобиль , и это абсолютное положение автомобиля и автомобиль соответственно, это скорость автомобиля , и это длина автомобиля и автомобиль соответственно, - коэффициент преобразования единицы из миль в час в м / с.
В частности, безопасный интервал и безопасное время вперед В Трубах автомобиль-следующая модель может быть выражена как:
Нелинейная модель Ньюэлла
Чтобы зафиксировать потенциальные нелинейные эффекты в динамике следования за автомобилем, Дж. Ф. Ньюэлл предложил нелинейную модель следования за автомобилем.[34] на основании эмпирических данных.В отличие от модели Pipes, основанной исключительно на правилах безопасного вождения, нелинейная модель Newell нацелена на получение правильной формы фундаментальных диаграмм (например, плотность-скорость, скорость потока, плотность-поток, интервал-скорость, темп-прогресс и т. Д. ). Нелинейную модель Ньюэлла можно описать как:
в котором это скорость автомобиля , время восприятия-реакции водителя , желаемая скорость, параметр, связанный с драйвером , расстояние между автомобилями и предшествующий автомобиль , это длина автомобиля .
Модель оптимальной скорости
Модель оптимальной скорости (OVM) была представлена Bando et al. в 1995 г. [35] основан на предположении, что каждый водитель пытается достичь оптимальной скорости в соответствии с разницей между транспортными средствами и разницей скоростей между предшествующим транспортным средством. В OVM ускорение / замедление транспортного средства п является функцией расстояния между автомобилями , скорость движущегося впереди автомобиля , а коэффициент чувствительности (который представляет чувствительность водителя к ускорению, большое значение указывает на агрессивного водителя, а маленькое значение означает осторожного водителя):
в котором - функция оптимальной скорости (OV-функция), ее можно выразить как:
OV-функция имеет два следующих свойства:
- OV-функция - это монотонно возрастающая функция.
- имеет верхнюю границу:
Модель интеллектуального водителя
Модель интеллектуального водителя широко используется в исследованиях Connected Vehicle (CV) и Connected and Autonomous Vehicle (CAV). Дополнительные сведения об этой модели, следующей за автомобилем, см. На веб-странице Википедии. Модель интеллектуального водителя.
Смотрите также
- Парадокс Браесса
- Поток данных
- Алгоритм Дейкстры
- Эпидемиология дорожно-транспортных происшествий
- Плавающие данные об автомобиле
- Инфракрасный регистратор трафика
- Ограничение полосы движения для грузовиков
- Управление дорожным движением
- Безопасность дорожного движения # Статистика
- Правило 184
- Счетчик трафика
- Транспортная инженерия
- Счетчики поворотных движений
использованная литература
- ^ Генри Лью (январь – февраль 1999 г.). "Теория транспортных потоков". Общественные дороги (Том 62, №4).
- ^ Райн, Джон. «Вместимость дорог» (PDF). В развитии. Получено 22 июля 2014.
- ^ В.Л. Knoop и W. Daamen (2017). «Процедура автоматической подгонки фундаментальной диаграммы». Transportmetrica B: Транспортная динамика. 5 (2): 133–148. Дои:10.1080/21680566.2016.1256239.
- ^ Лаваль, Хорхе А .; Тот, Кристофер С .; Чжоу, И (2014-12-01). «Экономная модель для формирования колебаний в моделях, следующих за автомобилем». Транспортные исследования, часть B: методологические. 70: 228–238. Дои:10.1016 / j.trb.2014.09.004. ISSN 0191-2615.
- ^ Линт, Дж. В. К. В., "Надежное прогнозирование времени в пути для автострад", докторская диссертация, Нидерландская исследовательская школа TRAIL, 2004 г.
- ^ Руководство по пропускной способности шоссе 2000
- ^ Сайт транспортного программного обеспечения SATURN ITS
- ^ Введение в Contram
- ^ Великобритания Департамент транспортаРуководство WebTag по проведению транспортных исследований
- ^ Кэссиди, M.J .; Бертини, Р.Л. (1999). "Некоторые особенности движения на узких местах автострады". Транспортные исследования, часть B: методологические. 33 (1): 25–42. Дои:10.1016 / S0191-2615 (98) 00023-X.
- ^ а б Питстик, Марк Э. «Измерение задержки и моделирование производительности на изолированных сигнальных пересечениях с использованием кумулятивных кривых». Отчет о транспортных исследованиях 1287 (1990)
- ^ Хуан Карлос Муньос и Хорхе А. Лаваль. «Метод графического решения оптимального динамического распределения трафика для перегруженной автострады и одного пункта назначения». Транспортные исследования, часть B: методологические (2006)
- ^ Минимизация вероятности возникновения перегрузки трафика в сети трафика
- ^ а б Сюй, Ван (2016). «Внедрение регулируемых ограничений скорости: предварительные испытания на Уайтмуд Драйв, Эдмонтон, Канада». Журнал транспортной инженерии. 142 (12): 05016007. Дои:10.1061 / (ASCE) TE.1943-5436.0000895.
- ^ Техасский транспортный институт A&M. «Пределы переменной скорости» (PDF). Управление движением. Техас A&M. Получено 2018-12-03.
- ^ Лаваль, Хорхе (2018). Теория транспортного потока.
- ^ Махмуд, Хизир; Город, Грэм Э. (июнь 2016 г.). «Обзор компьютерных инструментов для моделирования требований к энергии электромобилей и их влияния на распределительные сети». Прикладная энергия. 172: 337–359. Дои:10.1016 / j.apenergy.2016.03.100.
- ^ а б c d е Лайтхилл, М.Дж .; Whitham, G.B. (1955). «На кинематических волнах. I: Движение половодья в длинных реках. II: Теория транспортного потока на длинных переполненных дорогах». Труды Королевского общества. 229A (4): 281–345.
- ^ Ньюэлл, Гордон (1982). Приложения теории массового обслуживания (2-е изд.). Лондон: Чепмен и Холл.
- ^ Даганзо, Карлос (1994). «Модель передачи ячеек, часть II: сетевой трафик». Транспортные исследования, часть B: методологические. 28 (2): 279–293.
- ^ Кэссиди, Майкл Дж .; Ан, Соён (2005). «Поведение водителей с учетом очередности при слиянии перегруженных автострад» (PDF). Отчет о транспортных исследованиях: журнал Совета по исследованиям в области транспорта. 1934: 140–147. CiteSeerX 10.1.1.367.2080. Дои:10.3141/1934-15.
- ^ а б фигура отсутствует
- ^ а б c d е ж г Кернер, Борис С. (2013). «Критика общепринятых основ и методологий теории дорожного движения и транспорта: краткий обзор». Physica A: Статистическая механика и ее приложения. 392 (21): 5261–5282. Bibcode:2013PhyA..392.5261K. Дои:10.1016 / j.physa.2013.06.004.
- ^ ПИ. Ричардс, «Ударные волны на шоссе». Опер. Рез., 4, 42-51 (1956).
- ^ Даганзо, Карлос Ф. (1994). «Модель передачи ячеек: динамическое представление дорожного движения в соответствии с гидродинамической теорией». Транспортные исследования, часть B: методологические. 28 (4): 269–287. Дои:10.1016/0191-2615(94)90002-7.
- ^ Р. Херман, Э. В. Монтролл, Р. Б. Поттс и Р. В. Ротери, "Динамика движения: анализ устойчивости при следовании за автомобилем". Опер. Res., 7, 86-106 (1959).
- ^ Д.К. Газис, Р. Херман и Р. В. Ротери. «Нелинейные модели движения за лидером». Опер. Res., 9, 545-567 (1961).
- ^ Гриншилдс, Б. «Исследование пропускной способности». Слушания Совета по исследованиям шоссе, 14, 448–477 (1935))
- ^ а б Элефтериаду, Л. "Введение в теорию транспортных потоков". Оптимизация Springer и ее приложения, Vol. 84 (Springer, Берлин, 2014 г.)
- ^ J.G. Wardrop, "Некоторые теоретические аспекты исследования дорожного движения", в Proc. Инст. гражданского инж. II., 1, 325—362 (1952)
- ^ а б Т.С. Кун, "Структура научных революций". Четвертый выпуск. (Издательство Чикагского университета, Чикаго, Лондон, 2012 г.)
- ^ Кернер, Борис С .; Кленов, Сергей Л .; Шрекенберг, Майкл (2014). «Вероятностные физические характеристики фазовых переходов на узких местах автомагистралей: несоизмеримость трехфазной и двухфазной теории транспортных потоков». Phys. Ред. E. 89 (5): 052807. Bibcode:2014PhRvE..89e2807K. Дои:10.1103 / PhysRevE.89.052807. PMID 25353844.
- ^ Трубы, Луи А. (1953). «Оперативный анализ динамики движения». Журнал прикладной физики. 24 (3): 274–281. Bibcode:1953JAP .... 24..274P. Дои:10.1063/1.1721265.
- ^ Ньюэлл, Г. Ф. (1961). «Нелинейные эффекты в динамике следования за автомобилем». Исследование операций. 9 (2): 209–229. Дои:10.1287 / opre.9.2.209. JSTOR 167493.
- ^ Bando, M .; Hasebe, K .; Накаяма, А .; Шибата, А .; Сугияма, Ю. (1995). «Динамическая модель загруженности дорог и численное моделирование». Физический обзор E. 51 (2): 1035–1042. Bibcode:1995PhRvE..51.1035B. Дои:10.1103 / PhysRevE.51.1035. PMID 9962746.
дальнейшее чтение
Обзор современного состояния моделирования транспортных потоков:
- Н. Белломо, В. Кошиа, М. Делитала, О математической теории транспортных потоков I. Гидродинамическое и кинетическое моделирование. Математика. Мод. Meth. Приложение. Sc., Vol. 12, № 12 (2002) 1801–1843
- С. Маэривэ, Моделирование движения на автомагистралях: новейшие технологии, численный анализ данных и динамическое распределение трафика, Католический университет Лёвена, 2006 г.
- М. Гаравелло и Б. Пикколи, Поток трафика в сетях, Американский институт математических наук (AIMS), Спрингфилд, Миссури, 2006. стр. Xvi + 243 ISBN 978-1-60133-000-0
- Карлос Даганцо, «Основы транспорта и транспортных операций», Пергамон-Эльзевьер, Оксфорд, Великобритания (1997)
- Б.С. Кернер, Введение в современную теорию транспортных потоков и управление ими: долгий путь к теории трехфазного движения, Springer, Берлин, Нью-Йорк 2009
- Кэссиди, М.Дж. и Р.Л. Бертини. «Наблюдения на узком месте автострады». Транспорт и теория движения (1999).
- Даганзо, Карлос Ф. «Простая процедура анализа трафика». Сети и пространственная экономика 1.i (2001): 77–101.
- Линдгрен, Роджер В.Ф. «Анализ характеристик потока в очереди движения на немецкой автостраде». Государственный университет Портленда (2005).
- Ni, B. и J.D. Леонард. «Прямые методы определения характеристик потока трафика по определению». Отчет о транспортных исследованиях (2006).
Полезные книги с физической точки зрения:
- М. Трейбер и А. Кестинг, «Динамика транспортного потока», Springer, 2013 г.
- Б.С. Кернер, Физика дорожного движения, Springer, Берлин, Нью-Йорк 2004
- Поток трафика на arxiv.org
- Мэй, Адольф. Основы движения трафика. Прентис Холл, Энглвуд Клиффс, Нью-Джерси, 1990.
- Тейлор, Николас. Модель динамического распределения трафика Contram TRL 2003

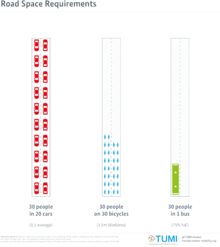

![{ displaystyle { begin {align} [rlr] v (t) & = x '(t) & { text {(speed)}} a (t) & = v' (t) = x '' (t) & { text {(ускорение)}} j (t) & = a '(t) = v' '(t) = x' '' (t) & { text {(рывок)} } конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9953552678a2b027fabc20905634d8d683082d3)









![{ textstyle a (x) = { frac {d [{ frac {1} {2}} v ^ {2}]} {dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8986488f8515c4a0a9afda31970d8f6e11967620)
![{ textstyle d [{ frac {1} {2}} v (x) ^ {2}] = a (x) dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7952f91c7cc6b138413ce44e3d8670f00de082ac)

































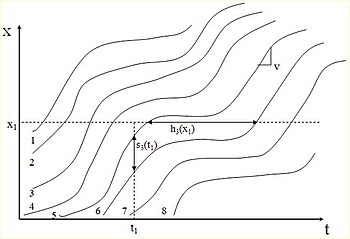










































![{ displaystyle v in [-w, u]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1dbb5f7ac403621be88071ce516db6fa548ee73)





































































































































































