WikiDer > Тимсорт

Тимсорт

Учебный класс	Алгоритм сортировки
Структура данных	Множество
Худший случай спектакль	${ Displaystyle О (п журнал п)}$[1][2]
Лучший случай спектакль	${ Displaystyle О (п)}$[3]
Средний спектакль	${ Displaystyle О (п журнал п)}$
Худший случай космическая сложность	${ Displaystyle О (п)}$

Тимсорт это гибридный стабильный алгоритм сортировки, происходит от Сортировка слиянием и вставка сортировки, предназначенный для хорошей работы с различными типами реальных данных. Это было реализовано Тим Питерс в 2002 году для использования в Язык программирования Python. Алгоритм находит подпоследовательности данных, которые уже упорядочены (запускаются), и использует их для более эффективной сортировки остатка. Это делается путем объединения прогонов до тех пор, пока не будут выполнены определенные критерии. Timsort является стандартным алгоритмом сортировки Python начиная с версии 2.3. Он также используется для сортировки массивов непримитивного типа в Java SE 7,^[4] на Платформа Android,^[5] в GNU Octave,^[6] на V8,^[7] Быстрый,^[8] и Ржавчина.^[9]

В нем используются методы из статьи Питера Макилроя 1993 года «Оптимистическая сортировка и теоретическая сложность информации».^[10]

Операция

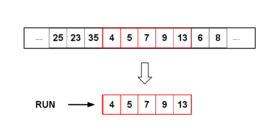
Timsort был разработан для использования бежит последовательных упорядоченных элементов, которые уже существуют в большинстве реальных данных, естественные пробеги. Он выполняет итерацию по элементам сбора данных в прогоны и одновременно помещает эти прогоны в стек. Каждый раз, когда пробеги на вершине стека соответствуют критерий слияния, они объединены. Это продолжается до тех пор, пока не будут пройдены все данные; затем все прогоны объединяются по два за раз, и остается только один отсортированный прогон. Преимущество объединения упорядоченных прогонов вместо слияния подсписок фиксированного размера (как это делается при традиционной сортировке слиянием) состоит в том, что оно уменьшает общее количество сравнений, необходимых для сортировки всего списка.

Каждый прогон имеет минимальный размер, который зависит от размера входных данных и определяется в начале алгоритма. Если серия меньше этого минимального размера, вставка сортировки используется для добавления дополнительных элементов в серию, пока не будет достигнут минимальный размер серии.

Критерии слияния

Прогоны вставляются в куча. Если |Z| ≤ |Y| + |Икс|, тогда Икс и Y объединяются и заменяются в стеке. Таким образом, слияние продолжается, пока все прогоны не удовлетворяют я. |Z| > |Y| + |Икс| и II. |Y| > |Икс|.

Timsort - это стабильный алгоритм сортировки (сохраняется порядок элементов с одинаковым ключом), который стремится выполнять сбалансированные слияния (слияние, таким образом, объединяет прогоны одинакового размера).

Чтобы добиться стабильности сортировки, объединяются только последовательные прогоны. Между двумя непоследовательными запусками может быть элемент с одним и тем же ключом элементов внутри прогонов, и объединение этих двух прогонов изменит порядок равных ключей. Пример этой ситуации ([] - это упорядоченные прогоны): [1 2 2] 1 4 2 [0 1 2]

В поисках сбалансированных слияний Timsort рассматривает три прогона на вершине стека, Икс, Y, Z, и поддерживает инварианты:

Если какой-либо из этих инвариантов нарушается, Y сливается с меньшим из Икс или же Z и инварианты снова проверяются. Как только инварианты сохранятся, можно начинать поиск нового прогона в данных.^[12] Эти инварианты поддерживают слияния как приблизительно сбалансированные, сохраняя при этом компромисс между откладыванием слияния для баланса и использованием новых запусков в кэш-память и относительно просто принимать решения о слиянии.

Объединить накладные расходы на пространство

Для слияния Timsort копирует элементы меньшего массива (X на этом рисунке) во временную память, затем сортирует и заполняет элементы в окончательном порядке в объединенное пространство X и Y.

Исходная реализация сортировки слиянием не на месте, и у нее накладные расходы на пространство N (размер данных). Существуют реализации сортировки слиянием на месте, но они требуют больших затрат времени. Чтобы достичь среднего срока, Timsort выполняет сортировку слиянием с небольшими затратами времени и меньшими затратами места, чем N.

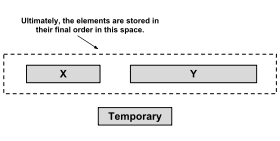
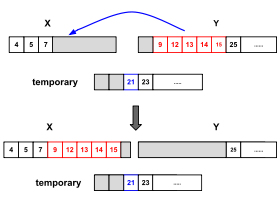
Сначала Timsort выполняет бинарный поиск чтобы найти место, где первый элемент второго прогона будет вставлен в первый упорядоченный прогон, сохраняя его в порядке. Затем он выполняет тот же алгоритм, чтобы найти место, где последний элемент первого прогона будет вставлен во второй упорядоченный прогон, сохраняя его упорядоченным. Элементы до и после этих местоположений уже находятся на своих местах, и их не нужно объединять. Затем меньший из оставшихся элементов двух прогонов копируется во временную память, а элементы объединяются с большей серией в теперь свободное пространство. Если первый прогон меньше, слияние начинается с самого начала; если второй меньше, слияние начинается в конце. Эта оптимизация снижает количество необходимых перемещений элементов, время работы и временные накладные расходы на пространство в общем случае.

Пример: необходимо объединить два прогона [1, 2, 3, 6, 10] и [4, 5, 7, 9, 12, 14, 17]. Обратите внимание, что оба прогона уже отсортированы по отдельности. Наименьший элемент второго прогона - 4, и его нужно будет добавить в 4-ю позицию первого прогона, чтобы сохранить его порядок (при условии, что первая позиция прогона равна 1). Самый большой элемент первого прогона - 10, и его нужно будет добавить в 5-ю позицию второго прогона, чтобы сохранить его порядок. Следовательно, [1, 2, 3] и [12, 14, 17] уже находятся в своих конечных положениях, и прогоны, в которых требуются перемещения элементов, - это [6, 10] и [4, 5, 7, 9]. Зная это, нам нужно только выделить временный буфер размером 2 вместо 5.

Направление слияния

Слияние может выполняться в обоих направлениях: слева направо, как при традиционной сортировке слиянием, или справа налево.

Галопирующий режим при слиянии

Элементы (отмеченные синей стрелкой) сравниваются, и меньший элемент перемещается в свое окончательное положение (указано красной стрелкой).

При отдельном объединении прогонов R1 и R2 сохраняется количество последовательных элементов, выбранных из прогона. Когда это число достигнет минимальный порог скачки (min_gallop), Timsort считает, что вполне вероятно, что многие последовательные элементы все еще могут быть выбраны из этого цикла, и переключается в режим галопирования. Предположим, что R1 отвечает за его запуск. В этом режиме алгоритм выполняет экспоненциальный поиск, также известный как поиск скачком, для следующего элемента x бега R2 в беге R1. Это делается в два этапа: первый находит диапазон (2^k − 1, 2^{к + 1} - 1) где x. На втором этапе выполняется двоичный поиск элемента x в диапазоне, найденном на первом этапе. Галопирующий режим - это попытка адаптировать алгоритм слияния к шаблону интервалов между элементами в прогонах.

Все красные элементы меньше синих (здесь 21). Таким образом, они могут быть перемещены куском в окончательный массив.

Галоп не всегда эффективен. В некоторых случаях режим галопирования требует большего количества сравнений, чем простой линейный поиск. Согласно тестам, проведенным разработчиком, галопирование выгодно только тогда, когда начальный элемент одного запуска не является одним из первых семи элементов другого запуска. Это подразумевает начальный порог 7. Чтобы избежать недостатков режима галопирования, предпринимаются два действия: (1) Когда галопирование оказывается менее эффективным, чем бинарный поиск, режим скачки выходит. (2) Успех или неудача галопа используются для корректировки min_gallop. Если выбранный элемент принадлежит к тому же массиву, который ранее возвращал элемент, min_gallop уменьшается на единицу, что способствует возвращению в режим галопом. В противном случае значение увеличивается на единицу, препятствуя возврату в режим галопирования. В случае случайных данных значение min_gallop становится настолько большим, что режим "галоп" никогда не повторяется.^[13]

По убыванию

Чтобы также использовать данные, отсортированные в порядке убывания, Timsort инвертирует строго убывающие прогоны, когда находит их, и добавляет их в стек прогонов. Поскольку нисходящие прогоны позже слепо меняются местами, исключение прогонов с равными элементами поддерживает стабильность алгоритма; т.е. равные элементы не будут перевернуты.

Минимальный размер тиража

Алгоритм Timsort ищет упорядоченные последовательности минимального размера, minruns, для выполнения сортировки.

Поскольку слияние наиболее эффективно, когда количество прогонов равно или немного меньше степени двойки, и заметно менее эффективно, когда количество прогонов немного больше, чем степень двойки, Timsort выбирает Minrun стараться обеспечить прежнее состояние.^[11]

Minrun выбирается из диапазона от 32 до 64 включительно, так что размер данных, деленный на Minrun, равна или немного меньше степени двойки. Последний алгоритм берет шесть наиболее значимых битов размера массива, добавляет один, если установлен какой-либо из оставшихся битов, и использует этот результат в качестве Minrun. Этот алгоритм работает для всех массивов, включая массивы меньше 64; для массивов размером 63 или меньше это устанавливает Minrun равным размеру массива, и Timsort сводится к сортировке вставкой.^[11]

Анализ

в худший случай, Timsort берет ${ Displaystyle О (п журнал п)}$ сравнения для сортировки массива п элементы. В лучшем случае, когда ввод уже отсортирован, он выполняется за линейное время, что означает, что это адаптивная сортировка алгоритм.^[3]

Это выгодно по сравнению с Quicksort для сортировки ссылок на объекты или указателей, потому что они требуют дорогостоящего косвенного обращения к памяти для доступа к данным и выполнения сравнений, а преимущества согласованности кэша Quicksort значительно снижаются.

Формальная проверка

В 2015 году голландские и немецкие исследователи из проекта EU FP7 ENVISAGE обнаружили ошибку в стандартной реализации Timsort.^[14]

В частности, инварианты для размеров серии стека обеспечивают жесткую верхнюю границу максимального размера требуемого стека. Реализация предварительно выделила стек, достаточный для сортировки 2⁶⁴ байтов ввода и избежать дальнейших проверок переполнения.

Однако гарантия требует, чтобы инварианты применялись к каждый группа из трех последовательных прогонов, но реализация проверила ее только для трех лучших.^[14] С использованием Ключ инструмент для формальная проверка программного обеспечения Java, исследователи обнаружили, что этой проверки недостаточно, и они смогли найти длины прогона (и входные данные, которые генерировали эти длины прогона), которые привели бы к нарушению инвариантов глубже в стеке после того, как вершина стека была слились.^[15]

Как следствие, для определенных входов выделенный размер недостаточен для хранения всех несвязанных прогонов. В Java это создает для этих входных данных исключение выхода за пределы массива. Наименьший вход, который вызывает это исключение в Java и Android v7, имеет размер 67108864 (2²⁶). (Более старые версии Android уже вызывали это исключение для определенных входов размера 65536 (2¹⁶))

Реализация Java была исправлена ​​путем увеличения размера предварительно выделенного стека на основе обновленного анализа наихудшего случая. В статье также показано формальными методами, как установить предполагаемый инвариант, проверив, что четыре самые верхние прогоны в стеке удовлетворяют двум правилам, указанным выше. Этот подход был принят Python^[16] и Android.

Рекомендации

дальнейшее чтение

• Оже, Николас; Никауд, Кирилл; Пивото, Карин (2015). «Стратегии слияния: от сортировки слиянием до TimSort». hal-01212839.
• Оже, Жуже, Нико, Пивото (2018). «О сложности TimSort в наихудшем случае». ESA 2018.
• Сэм Басс, Александр Кноп. «Стратегии стабильной сортировки слиянием». SODA 2019.

внешняя ссылка

• timsort.txt - оригинальное объяснение Тима Питерса