WikiDer > Изменение давления по вертикали
Изменение давления по вертикали это вариация в давление как функция высота. В зависимости от жидкость в рассматриваемом контексте и в контексте, на который делается ссылка, он также может значительно различаться по размерам, перпендикулярным высоте, и эти вариации имеют значение в контексте сила градиента давления и его эффекты. Однако вертикальное отклонение особенно велико, так как оно является результатом натяжения сила тяжести на жидкости; а именно, для того же самого данного флюида уменьшение высоты внутри него соответствует более высокому столбу флюида, утяжеляющемуся в этой точке.
Основная формула
Относительно простая версия [1] изменения вертикального давления жидкости просто состоит в том, что разница давлений между двумя высотами является продуктом изменения высоты, силы тяжести и плотность. Уравнение выглядит следующим образом:
- , и
куда
- п давление,
- ρ это плотность,
- грамм является ускорение свободного падения, и
- час высота.
Символ дельты указывает на изменение данной переменной. С грамм отрицательно, увеличение высоты будет соответствовать уменьшению давления, что согласуется с ранее упомянутыми рассуждениями о весе столба жидкости.
Когда плотность и сила тяжести приблизительно постоянны (то есть при относительно небольших изменениях высоты), простое умножение разницы высот, силы тяжести и плотности даст хорошее приближение разницы давления. Если разные жидкости накладываются друг на друга, общий перепад давления может быть получен путем сложения двух перепадов давления; первая - от точки 1 до границы, вторая - от границы до точки 2; который просто включал бы замену ρ и Δчас значения для каждой жидкости и взятие суммы результатов. Если плотность жидкости зависит от высоты, математическая интеграция потребуется.
Могут ли плотность и гравитация считаться постоянными или нет, зависит от уровня точность необходимо, но и на шкала длины разницы в высоте, поскольку сила тяжести и плотность также уменьшаются с увеличением высоты. В частности, для плотности имеет значение рассматриваемая жидкость; морская вода, например, считается несжимаемая жидкость; его плотность может меняться с высотой, но гораздо менее значительно, чем у воздуха. Таким образом, плотность воды можно более разумно считать постоянной, чем плотность воздуха, и при одинаковой разнице высот перепады давления в воде примерно одинаковы на любой высоте.
Гидростатический парадокс
| Викискладе есть медиафайлы по теме Гидростатический парадокс. |
Барометрическая формула зависит только от высоты жидкостной камеры, а не от ее ширины или длины. При достаточно большой высоте можно добиться любого давления. Эта особенность гидростатики получила название гидростатический парадокс. По выражению В. Х. Безант,[2]
- Любое количество жидкости, даже небольшое, может выдерживать любой вес, даже большой.
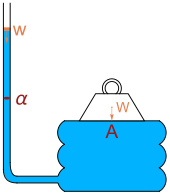
Голландский ученый Саймон Стевин был первым, кто объяснил парадокс математически.[3] В 1916 г. Ричард Глейзбрук упомянул гидростатический парадокс, когда описал устройство, которое он приписал Паскаль: тяжелый вес W лежит на доске с площадью А покоится на камере для жидкости, соединенной с вертикальной трубкой с площадью поперечного сечения α. Лить воду веса ш вниз по трубке поднимет тяжелый груз. Баланс сил приводит к уравнению
Глейзбрук говорит: «Сделав значительную площадь доски и маленькой трубы, мы получили большой вес. W может поддерживаться небольшим весом ш воды. Этот факт иногда называют гидростатическим парадоксом ».[4]
При обучении этому феномену используются демонстрации гидростатического парадокса.[5][6]
В контексте атмосферы Земли
Если нужно проанализировать изменение вертикального давления атмосфера Земли, масштаб длины очень значителен (тропосфера одинокие несколько километров высокий; термосфера несколько сотен километров), а вовлеченная жидкость (воздух) сжимаема. Гравитацию все еще можно обоснованно считать константой, потому что масштабы длин порядка километров все еще малы по сравнению с радиусом Земли, который в среднем составляет около 6371 км.[7] а гравитация - это функция расстояния от ядра Земли.[8]
С другой стороны, плотность меняется более существенно с ростом. Это следует из закон идеального газа который
куда
- м средний масса за воздух молекула,
- п давление в данной точке,
- k это Постоянная Больцмана,
- Т это температура в кельвины.
Проще говоря, плотность воздуха зависит от давления воздуха. Учитывая, что давление воздуха также зависит от плотности воздуха, было бы легко создать впечатление, что это было круговое определение, но это просто взаимозависимость разных переменных. Это дает более точную формулу вида
куда
- пчас давление на высоте час,
- п0 давление в контрольной точке 0 (обычно на уровне моря),
- м масса, приходящаяся на молекулу воздуха,
- грамм это ускорение силы тяжести,
- час это высота от опорной точки 0,
- k это Постоянная Больцмана,
- Т это температура в кельвинах.
Поэтому вместо давления линейный функция высоты, как и следовало ожидать от более простой формулы, приведенной в разделе "Основная формула", она более точно представлена как экспоненциальная функция высоты.
Обратите внимание, что в этом упрощении температура считается постоянной, хотя температура также изменяется с высотой. Однако изменение температуры в нижних слоях атмосферы (тропосфера, стратосфера) только в десятках степеней, в отличие от их термодинамическая температура, который исчисляется сотнями, поэтому изменение температуры достаточно мало и поэтому игнорируется. Для небольших перепадов высот, в том числе сверху вниз даже самых высоких зданий (например, Си-Эн Тауэр) или для гор сопоставимого размера изменение температуры легко будет в пределах однозначных цифр. (Смотрите также скорость отклонения.)
Альтернативный вывод, представленный Аэрокосмическим обществом Портленда,[9] вместо этого используется для определения высоты как функции давления. Это может показаться нелогичным, поскольку давление зависит от высоты, а не наоборот, но такая формула может быть полезна для определения высоты на основе разницы давлений, когда известно последнее, а не первое. Для разных приближений представлены разные формулы; для сравнения с предыдущей формулой первой в статье будет ссылка на формулу, в которой применяется такое же приближение постоянной температуры; в таком случае:
где (со значениями, использованными в статье)
- z высота в метрах,
- р это удельная газовая постоянная = 287,053 Дж / (кг · К)
- Т абсолютная температура в градусах Кельвина = 288,15 К на уровне моря,
- грамм ускорение свободного падения = 9.80665 РС2 на уровне моря,
- п давление в данной точке на высоте z в Паскалях, и
- п0 давление в опорной точке = 101,325 Па на уровне моря.
Более общая формула, полученная в той же статье, учитывает линейное изменение температуры как функцию высоты (градиент) и сводится к приведенному выше значению, когда температура постоянна:
куда
- L - атмосферный градиент (изменение температуры, деленное на расстояние) = −6.5×10−3 К / м, и
- Т0 - температура в той же контрольной точке, для которой п = п0
а остальные количества такие же, как указано выше. Это рекомендуемая формула.
Смотрите также
Рекомендации
- ^ «Барометрическая формула».
- ^ Безант, В. Х. (1900). Элементарная гидростатика. Интернет-архив. Джордж Белл и сыновья. п. 11.
- ^ Ру, Софи (25 сентября 2012 г.). Механизация естественной философии. Springer Science & Business Media. п. 160. ISBN 9400743459.
Стевин представляет собой оригинальную математическую демонстрацию так называемого гидростатического парадокса.
- ^ Глейзбрук, Ричард (1916). Гидростатика: базовый учебник, теоретический и практический. Интернет-архив. Издательство Кембриджского университета. п. 42.
- ^ Гринслейд младший, Томас Б. «Гидростатический парадокс». Kenyon College.
- ^ Объяснение на YouTube
- ^ «Радиус Земли».
- ^ "Закон всемирного тяготения Ньютона".
- ^ «Быстрый вывод, связывающий высоту с атмосферным давлением» (PDF). Архивировано из оригинал (PDF) на 2011-09-28. Получено 2011-11-30.
- Мерлино, Роберт Л. (2003). «Статика - жидкости в состоянии покоя». Получено 2014-11-20.