WikiDer > Лемма Витали о покрытии

В математика, то Лемма Витали о покрытии это комбинаторно-геометрический результат обычно используется в теория меры из Евклидовы пространства. Эта лемма представляет собой промежуточный шаг, представляющий самостоятельный интерес, в доказательстве Теорема Витали о покрытии. Теорема о покрытии принадлежит Итальянский математик Джузеппе Витали.^[1] Теорема утверждает, что можно покрыть с точностью до Набор пренебрежимо малый по Лебегу, данное подмножество E из р^d несвязной семьей, извлеченной из Виталий покрытие из E.

Лемма Витали о покрытии

Визуализация леммы в ${displaystyle mathbb {R} ^ {1}}$.

Вверху: набор шаров; зеленые шары - непересекающиеся подколлекции. Внизу: подколлекция с трехкратным радиусом покрывает все шары.

Утверждение леммы

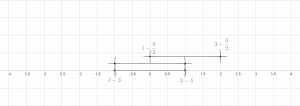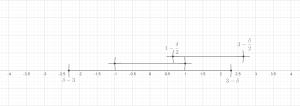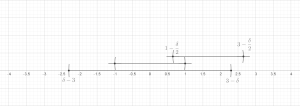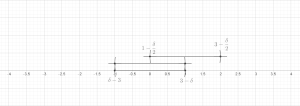
• Конечная версия: Позволять ${displaystyle B_ {1}, ldots, B_ {n}}$ быть любым конечным набором мячи содержится в d-размерный Евклидово пространство р^d (или, в более общем смысле, в произвольной метрическое пространство). Тогда существует подколлекция ${displaystyle B_ {j_ {1}}, B_ {j_ {2}}, точки, B_ {j_ {m}}}$ этих шаров, которые непересекающийся и удовлетворить

${displaystyle B_ {1} чашка B_ {2} чашка ldots чашка B_ {n} substeq 3B_ {j_ {1}} чашка 3B_ {j_ {2}} чашка ldots чашка 3B_ {j_ {m}}}$

куда ${displaystyle 3B_ {j_ {k}}}$ обозначает шар с тем же центром, что и ${displaystyle B_ {j_ {k}}}$ но с трехкратным радиусом.

• Бесконечная версия: Позволять ${displaystyle {B_ {j}: jin J}}$ - произвольный набор шаров из р^d (или, в более общем смысле, в сепарабельном метрическом пространстве) такое, что

${displaystyle sup, {mathrm {rad} (B_ {j}): jin J}$

куда ${displaystyle mathrm {rad} (B_ {j})}$ обозначает радиус шара B_j. Тогда существует счетная подгруппа

${displaystyle {B_ {j}: jin J '}, quad J'subset J}$

шаров из исходной коллекции, которые не пересекаются и удовлетворяют

${displaystyle igcup _ {jin J} B_ {j} substeq igcup _ {jin J '} 5, B_ {j}.}$

Комментарии.

• Шары могут иметь форму B = {у : d(у, c) < р} (открытый шар с центром c и радиус р) или же B = {у : d(у, c) ≤ р}. Тогда 3B (или 5B) обозначает шар той же формы, с 3р (или 5р) замена р. Обратите внимание, что определение мячей требует р > 0.
• в бесконечная версия, набор шаров можно счетный или же бесчисленный.
• Результат может потерпеть неудачу, если радиусы не ограничены: рассмотрим семейство всех шаров с центром в 0 в р^d; любое непересекающееся подсемейство состоит только из одного шара B, и 5B не содержит всех мячей в этом семействе.
• В контексте общего метрического пространства (т. Е. Необязательно разделимого) результирующая подгруппа не может быть счетно бесконечной.

Доказательство

Конечная версия

Без ограничения общности будем предполагать, что набор шаров не пустой; то есть, п > 0. Пусть ${displaystyle B_ {j_ {1}}}$ быть шаром наибольшего радиуса. Индуктивно предположим, что ${displaystyle B_ {j_ {1}}, точки, B_ {j_ {k}}}$ были выбраны. Если есть мяч в ${displaystyle B_ {1}, точки, B_ {n}}$ это не пересекается с ${displaystyle B_ {j_ {1}} чашка B_ {j_ {2}} чашка cdots чашка B_ {j_ {k}}}$, позволять ${displaystyle B_ {j_ {k + 1}}}$ - такой шар с максимальным радиусом (произвольно разрывая связи), иначе положим м := k и закончим индуктивное определение.

Теперь установите ${displaystyle X: = igcup _ {k = 1} ^ {m} 3, B_ {j_ {k}}}$. Осталось показать, что ${displaystyle B_ {i} subset X}$ для каждого ${displaystyle i = 1,2, dots, n}$. Это ясно, если ${displaystyle iin {j_ {1}, dots, j_ {m}}}$. В противном случае обязательно найдутся ${displaystyle kin {1, dots, m}}$ такой, что B_я пересекает ${displaystyle B_ {j_ {k}}}$ и радиус ${displaystyle B_ {j_ {k}}}$ по крайней мере такой же большой, как у B_я. В неравенство треугольника тогда легко следует, что ${displaystyle B_ {i} подмножество 3, B_ {j_ {k}} подмножество X}$, по мере необходимости. Это завершает доказательство конечной версии.

Бесконечная версия

Позволять F обозначим совокупность всех шаров B_j, j ∈ J, которые приведены в заявлении лемма о покрытии. Следующий результат дает некоторую непересекающуюся подколлекцию грамм из F. Если эта подколлекция грамм описывается как ${displaystyle {B_ {j}, jin J '}}$, собственность грамм, изложенное ниже, легко доказывает, что

${displaystyle igcup _ {jin J} B_ {j} substeq igcup _ {jin J '} 5, B_ {j}.}$

Точная форма леммы о покрытии. Позволять  F - набор (невырожденных) шаров в метрическом пространстве с ограниченными радиусами. Существует непересекающаяся подгруппа  грамм из  F со следующим свойством:

каждый шар B в  F пересекает шар C в  грамм такое, что B ⊂ 5 C.

(Вырожденные шары содержат только центр; они исключены из этого обсуждения.)
Позволять р - супремум радиусов шаров в F. Рассмотрим разбиение F в подколлекции F_п, п ≥ 0, состоящий из шаров B радиус которого находится в (2^−п−1р, 2^−пр]. Последовательность грамм_п, с грамм_п ⊂ F_п, определяется индуктивно следующим образом. Сначала установите ЧАС₀ = F₀ и разреши грамм₀ - максимальное непересекающееся подмножество ЧАС₀. При условии, что грамм₀,...,грамм_п были выбраны, пусть

${displaystyle mathbf {H} _ {n + 1} = {Bin mathbf {F} _ {n + 1}: Bcap C = emptyset, forall Cin mathbf {G} _ {0} cup mathbf {G} _ {1} чашка ldots cup mathbf {G} _ {n}},}$

и разреши грамм_п+1 - максимальное непересекающееся подмножество ЧАС_п+1. Подколлекция

${displaystyle mathbf {G}: = igcup _ {n = 0} ^ {infty} mathbf {G} _ {n}}$

из F удовлетворяет требованиям: грамм является непересекающимся набором, и каждый шар B ∈ F пересекает мяч C ∈ грамм такой, что B ⊂ 5 C.
Действительно, пусть п быть таким, чтобы B принадлежит F_п. Либо B не принадлежит ЧАС_п, что означает п > 0 и означает, что B пересекает шар из объединения грамм₀,...,грамм_п−1, или же B ∈ ЧАС_п и по максимальности грамм_п, B пересекает мяч в грамм_п. В любом слючае, B пересекает мяч C что принадлежит к союзу грамм₀,...,грамм_п. Такой мяч C имеет радиус> 2^−п−1р. Поскольку радиус B ≤ 2^−пр, это в два раза меньше, чем у C и заключение B ⊂ 5 C следует из неравенства треугольника, как и в конечном варианте.^[2]

Замечания

• Константа 5 не оптимальна. Если масштаб c^−п, c > 1, используется вместо 2^−п для определения F_п, окончательное значение 1 + 2c вместо 5. Любая константа больше 3 дает правильную формулировку леммы, но не 3.
• В наиболее общем случае произвольного метрического пространства для выбора максимальной непересекающейся подгруппы требуется форма Лемма Цорна.
• Используя более тонкий анализ, когда исходная коллекция F это Виталий покрытие подмножества E из р^d, показывает, что подколлекция грамм, определенная в приведенном выше доказательстве, покрывает E вплоть до пренебрежимо малого по Лебегу множества. ^[3]

Приложения и метод использования

Применение леммы Витали состоит в доказательстве Максимальное неравенство Харди – Литтлвуда. Как и в этом доказательстве, лемма Витали часто используется, когда мы, например, рассматриваем d-размерный Мера Лебега, ${displaystyle lambda _ {d}}$, из набор E ⊂ р^d, который, как мы знаем, содержится в объединении некоторого набора шаров ${displaystyle {B_ {j}: jin J}}$, каждый из которых имеет меру, которую нам легче вычислить, или особое свойство, которое хотелось бы использовать. Следовательно, если мы вычислим меру этого объединения, у нас будет верхняя оценка меры E. Однако трудно вычислить меру объединения всех этих шаров, если они перекрываются. По лемме Витали мы можем выбрать подколлекцию ${displaystyle {B_ {j}: jin J '}}$ который не пересекается и такой, что ${displaystyle igcup _ {jin J '} 5B_ {j} supset igcup _ {jin J} B_ {j} supset E}$. Следовательно,

${displaystyle lambda _ {d} (E) leq lambda _ {d} {Bigl (} igcup _ {jin J} B_ {j} {Bigr)} leq lambda _ {d} {Bigl (} igcup _ {jin J ' } 5B_ {j} {Bigr)} leq sum _ {jin J '} lambda _ {d} (5B_ {j}).}$

Теперь, так как увеличение радиуса d-мерный шар в 5 раз увеличивает его объем в 5 раз^d, мы знаем это

${displaystyle sum _ {jin J '} lambda _ {d} (5B_ {j}) = 5 ^ {d} sum _ {jin J'} lambda _ {d} (B_ {j})}$

и поэтому

${displaystyle lambda _ {d} (E) leq 5 ^ {d} sum _ {jin J '} lambda _ {d} (B_ {j}).}$

Теорема Витали о покрытии

В теореме о покрытии цель состоит в том, чтобы покрыть, вплоть до «ничтожный набор», данный набор E ⊆ р^d непересекающейся подколлекцией, извлеченной из Виталий покрытие заE : а Виталий класс или же Виталий покрытие ${displaystyle {mathcal {V}}}$ за E набор таких множеств, что для каждого Икс ∈ E и δ > 0 существует множество U в коллекции ${displaystyle {mathcal {V}}}$ такой, что Икс ∈ U и диаметр из U не равно нулю и меньше чемδ.

В классическом сеттинге Виталия,^[1] ничтожный набор - это Незначительный набор Лебега, но меры, отличные от меры Лебега, и пространства, отличные от р^d также учитывались, как показано в соответствующем разделе ниже.

Полезно следующее наблюдение: если ${displaystyle {mathcal {V}}}$ накрывает Витали E и если E содержится в открытом наборе Ω ⊆ р^d, то подколлекция множеств U в ${displaystyle {mathcal {V}}}$ которые содержатся в Ω также покрытие Витали для E.

Теорема Витали о покрытии меры Лебега

Следующая теорема о покрытии для меры Лебега λ_d связано с Лебег (1910). Коллекция ${displaystyle {mathcal {V}}}$ измеримых подмножеств р^d это обычная семья (в смысле Лебег), если существует постоянная C такой, что

${displaystyle mathrm {diam} (V) ^ {d} leq C, lambda _ {d} (V)}$

для каждого набора V в коллекции ${displaystyle {mathcal {V}}}$.
Семья кубиков - пример правильной семьи ${displaystyle {mathcal {V}}}$, как и семья ${displaystyle {mathcal {V}}}$(м) прямоугольников в р² так, чтобы соотношение сторон оставалось между м⁻¹ и м, для некоторых фиксированных м ≥ 1. Если на р^d, семейство шаров для метрики, связанной с нормой, является другим примером. Напротив, семья все прямоугольники в р² является нет обычный.

Теорема. Позволять E ⊆ р^d - измеримое множество с конечной мерой Лебега, и пусть ${displaystyle {mathcal {V}}}$ регулярное семейство замкнутых подмножеств р^d это накрытие Витали для E. Тогда существует конечная или счетно бесконечная непересекающаяся подгруппа ${displaystyle {U_ {j}} substeq {mathcal {V}}}$ такой, что

${displaystyle lambda _ {d} {Bigl (} Esetminus igcup _ {j} U_ {j} {Bigr)} = 0.}$

Исходный результат Виталий (1908) является частным случаем этой теоремы, в котором d = 1 и ${displaystyle {mathcal {V}}}$ представляет собой набор интервалов, который является покрытием Витали для измеримого подмножества E вещественной прямой конечной меры.
Приведенная выше теорема остается верной без предположения, что E имеет конечную меру. Это достигается применением результата о покрытии в случае конечной меры для любого целого числа п ≥ 0, на долю E содержится в открытом кольцевом пространстве Ω_п очков Икс такой, что п < |Икс| < п+1.^[4]

Схожая теорема о покрытии - это Теорема Безиковича о покрытии. К каждой точке а подмножества А ⊆ р^d, евклидов шар B(а, р_а) с центром а и положительный радиус р_а назначается. Затем, как в теореме Витали, выбирается подколлекция этих шаров, чтобы покрыть А определенным образом. Основные отличия от теоремы Витали о покрытии заключаются в том, что, с одной стороны, требование Витали о непересекаемости ослаблено до того факта, что число N_Икс выбранных шаров, содержащих произвольную точку Икс ∈ р^d ограничено константой B_d в зависимости только от размера d; с другой стороны, выбранные шары покрывают набор А всех данных центров.^[5]

Теорема Витали о покрытии для меры Хаусдорфа

У кого-то может быть аналогичная цель при рассмотрении Мера Хаусдорфа вместо меры Лебега. В этом случае применима следующая теорема.^[6]

Теорема. Позволять ЧАС^s обозначать s-мерная мера Хаусдорфа, пусть E ⊆ р^d быть ЧАС^s-измеримый установить и ${displaystyle {mathcal {V}}}$ класс замкнутых множеств Витали для E. Тогда существует (конечное или счетно бесконечное) непересекающееся подмножество ${displaystyle {U_ {j}} substeq {mathcal {V}}}$ так что либо

${displaystyle H ^ {s} left (E ackslash igcup _ {j} U_ {j} ight) = 0 {mbox {or}} sum _ {j} mathrm {diam} (U_ {j}) ^ {s} = infty.}$

Кроме того, если E имеет конечный s-мерная мера Хаусдорфа, то для любой ε > 0, мы можем выбрать эту подколлекцию {U_j} такой, что

${displaystyle H ^ {s} (E) leq sum _ {j} mathrm {diam} (U_ {j}) ^ {s} + varepsilon.}$

Из этой теоремы следует приведенный выше результат Лебега. Действительно, когда s = d, мера Хаусдорфа ЧАС^s на р^d совпадает с кратным d-мерная мера Лебега. Если непересекающаяся коллекция ${displaystyle {U_ {j}}}$ является регулярным и содержится в измеримой области B с конечной мерой Лебега, то

${displaystyle sum _ {j} mathrm {diam} (U_ {j}) ^ {d} leq Csum _ {j} lambda _ {d} (U_ {j}) leq C, lambda _ {d} (B) < + infty}$

что исключает вторую возможность первого утверждения предыдущей теоремы. Следует, что E покрывается с точностью до множества, которым можно пренебречь по Лебегу, выбранной непересекающейся подгруппой.

От леммы о покрытии к теореме о покрытии

Лемму о покрытии можно использовать как промежуточный шаг в доказательстве следующей основной формы теоремы Витали о покрытии. На самом деле нужно еще немного, а именно точная форма леммы о покрытии полученный в «доказательство бесконечной версии».

Теорема. Для каждого подмножества E из  р^d и все каверы Виталия на E по сборнику  F замкнутых шаров существует непересекающаяся подгруппа  грамм покрывающее E до множества, пренебрежимо малым по Лебегу.

Без ограничения общности можно считать, что все шары в F невырождены и имеют радиус ≤ 1. По Уточненная форма леммы о покрытиисуществует непересекающаяся подгруппа грамм из F так что каждый мяч B ∈ F пересекает мяч C ∈ грамм для которого B ⊂ 5 C. Позволять р > 0, и пусть Z обозначим множество точек z ∈ E которые не содержатся ни в одном шаре из грамм и принадлежат к открыто мяч B(р) радиуса р, с центром в 0. Достаточно показать, что Z пренебрежимо мало по Лебегу, для каждого данного р.

Позволять грамм обозначим подколлекцию этих шаров в грамм это встреча B(р). Рассмотрим разбиение грамм в наборы грамм_п, п ≥ 0, состоящий из шаров радиуса в (2^{−n − 1}, 2⁻ⁿ]. Любой мяч B в F что встречает B(р) содержится в B(р+2). Из свойства дизъюнктности грамм который

${displaystyle sum {lambda _ {d} (C): Cin G} = sum _ {n = 0} ^ {infty} {Bigl (} sum {lambda _ {d} (C): Cin G_ {n}} { Bigr)} leq lambda _ {d} (B (r + 2)) <+ infty.}$

Отсюда следует, что грамм_п является конечным множеством для каждого п. Данныйε > 0, мы можем выбрать N такой, что

${displaystyle sum {lambda _ {d} (C): Cin G_ {n} ,, n> N}$

Позволять z ∈ Z быть исправленным. По определению Z, эта точка z не принадлежит закрытому множеству K равный (конечному) объединению шаров в грамм_k, k ≤ N. По свойству покрытия Витали можно найти мяч B ∈ F содержащий z, содержалась в B(р) и не пересекаются с K. В собственности грамм, шар B встречает C и входит в 5C для какого-то мяча C ∈ грамм. Видно, что C ∈ грамм потому что C пересекает B(р), но C не принадлежит ни к какой семье грамм_k, k ≤ N, поскольку B встречает C но не пересекается с K. Это доказывает, что каждая точка z ∈ Z содержится в объединении 5C, когда C варьируется в грамм_п, п > N, следовательно

${displaystyle Zsubset U_ {N}: = igcup, {5, C: Cin G_ {n} ,, n> N}}$

и

${displaystyle lambda _ {d} (U_ {N}) leq sum {lambda _ {d} (5, C): Cin G_ {n} ,, n> N} = 5 ^ {d} sum {lambda _ {d } (C): Cin G_ {n} ,, n> N} <5 ^ {d} varepsilon.}$

С ε > 0 произвольно, это показывает, что Z незначительно.^[7]

Бесконечномерные пространства

Теорема Витали о покрытии не верна в бесконечномерных условиях. Первый результат в этом направлении дал Дэвид Прейсс в 1979 г .:^[8] существует Гауссова мера γ на (бесконечномерном) отделяемый Гильбертово пространство ЧАС так что теорема Витали о покрытии неверна для (ЧАС, Борель (ЧАС), γ). Этот результат был усилен в 2003 году Ярославом Тишером: теорема Витали о покрытии фактически неверна для каждый бесконечномерная гауссовская мера на любом (бесконечномерном) сепарабельном гильбертовом пространстве.^[9]

Смотрите также

• Теорема Безиковича о покрытии

Примечания

Рекомендации

• Эванс, Лоуренс С .; Гариепи, Рональд Ф. (1992), Теория меры и тонкие свойства функций, Исследования по высшей математике, Бока-Ратон, Флорида: CRC Press, стр. viii + 268, ISBN 0-8493-7157-0, МИСТЕР 1158660, Zbl 0804.28001
• Фалконер, Кеннет Дж. (1986), Геометрия фрактальных множеств, Кембриджские трактаты по математике, 85, Кембридж: Издательство Кембриджского университета, стр. xiv + 162, ISBN 0-521-25694-1, МИСТЕР 0867284, Zbl 0587.28004
• "Теорема Витали", Энциклопедия математики, EMS Press, 2001 [1994]
• Лебег, Анри (1910), "Sur l'intégration des fonctions прекращается", Научные Анналы Высшей Нормальной Школы, 27: 361–450, Дои:10.24033 / asens.624, JFM 41.0457.01
• Натансон, И. П. (1955), Теория функций действительного переменного, Нью-Йорк: Издательство Frederick Ungar Publishing Co., п. 277, г. МИСТЕР 0067952, Zbl 0064.29102
• Прейсс, Дэвид (1979), "Гауссовские меры и теоремы о покрытии", Commentatione Mathematicae Universitatis Carolinae, 20 (1): 95–99, ISSN 0010-2628, МИСТЕР 0526149, Zbl 0386.28015
• Штейн, Элиас М.; Шакарчи, Рами (2005), Реальный анализ. Теория меры, интегрирование и гильбертовы пространства, Принстонские лекции по анализу, III, Принстон, штат Нью-Джерси: Princeton University Press, pp. Xx + 402, ISBN 0-691-11386-6, МИСТЕР 2129625, Zbl 1081.28001
• Тишер, Ярослав (2003), "Теорема Витали о покрытии в гильбертовом пространстве", Труды Американского математического общества, 355 (8): 3277–3289 (электронная), Дои:10.1090 / S0002-9947-03-03296-3, МИСТЕР 1974687, Zbl 1042.28014
• Витали, Джузеппе (1908) [17 декабря 1907], "Sui gruppi di punti e sulle funzioni di variabili reali", Atti dell'Accademia delle Scienze di Torino (на итальянском), 43: 75–92, JFM 39.0101.05 (Перевод названия) "О группах точек и функциях вещественных переменных"- статья, содержащая первое доказательство Теорема Витали о покрытии.