WikiDer > Волновод - Википедия

А волновод это структура, которая направляет волны, такие как электромагнитные волны или же звук, с минимальными потерями энергии за счет ограничения передачи энергии в одном направлении. Без физического ограничения волновода амплитуды волн уменьшаются согласно закон обратных квадратов поскольку они расширяются в трехмерное пространство.
Существуют разные типы волноводов для разных типов волн. Оригинальный и самый распространенный[1] значение - полая проводящая металлическая труба, используемая для передачи высоких частот радиоволны, особенно микроволны. Диэлектрические волноводы используются на более высоких радиочастотах, а прозрачные диэлектрические волноводы и оптические волокна служат волноводами для света. В акустика, воздуховоды и рога используются в качестве волноводов для звука в музыкальных инструментах и музыкальные колонки, а металлические стержни специальной формы проводят ультразвуковые волны в ультразвуковая обработка.
Геометрия волновода отражает его функцию; В дополнение к более распространенным типам, которые направляют волну в одном измерении, существуют двумерные пластинчатые волноводы, которые ограничивают волны в двух измерениях. Частота проходящей волны также определяет размер волновода: каждый волновод имеет длина волны отсечки определяется своими размерами и не проводит волны большей длины; ан оптоволокно что направляет свет не будет передавать микроволны которые имеют гораздо большую длину волны. Некоторые естественные структуры также могут действовать как волноводы. В ГНФАР канал слой в океане может направлять звук китовая песня через огромные расстояния.[2] Любая форма поперечного сечения волновода может поддерживать электромагнитные волны. Неправильные формы трудно анализировать. Обычно используются волноводы прямоугольной и круглой формы.
Принцип

В открытом космосе волны распространяются во всех направлениях как сферические волны. Мощность волны падает с расстоянием р от источника как квадрат расстояния (закон обратных квадратов). Волновод ограничивает распространение волны в одном измерении, так что в идеальных условиях волна не теряет мощности при распространении. отражение у стенок волны ограничены внутренней частью волновода.
Использует
Использование волноводов для передачи сигналов было известно еще до появления этого термина. Явление звуковых волн, проходящих через натянутый провод, было известно давно, как и звук через полую трубу, такую как пещера или медицинские стетоскоп. Другое использование волноводов - передача мощности между компонентами системы, такими как радио, радары или оптические устройства. Волноводы - фундаментальный принцип волноводные испытания (GWT), один из многих методов неразрушающая оценка.
Конкретные примеры:
- Оптические волокна передают свет и сигналы на большие расстояния с низким затуханием и широким используемым диапазоном длин волн.
- В микроволновая печь волновод передает мощность от магнетрон, где образуются волны, в варочную камеру.
- В радаре волновод передает радиочастотную энергию к антенне и от нее, где сопротивление должны быть согласованы для эффективной передачи энергии (см. ниже).
- Прямоугольные и круглые волноводы обычно используются для подключения источников параболических антенн к их электронике, будь то малошумящие приемники или усилители / передатчики мощности.
- Волноводы используются в научных инструментах для измерения оптических, акустических и упругих свойств материалов и объектов. Волновод можно соприкасать с образцом (как в медицинское УЗИ), и в этом случае волновод обеспечивает сохранение мощности испытательной волны, или образец может быть помещен внутрь волновода (как при измерении диэлектрической проницаемости[3]), чтобы можно было тестировать более мелкие объекты и повышать точность.
- Линии передачи это особый тип волновода, который очень часто используется.
История
Эта секция дубликаты объем других разделов, конкретно, Волновод (электромагнетизм) # История. (Ноябрь 2020) |
Первая структура для направляющих волн была предложена Дж. Дж. Томсон в 1893 г. и впервые экспериментально проверен Оливер Лодж в 1894 году. Первый математический анализ электромагнитных волн в металлическом цилиндре был проведен Лорд Рэйли в 1897 г.[4]Для звуковых волн лорд Рэлей опубликовал полный математический анализ режимы распространения в его основополагающей работе «Теория звука».[5] Джагадиш Чандра Босе исследовал миллиметровые длины волн используя волноводы, и в 1897 году описал Королевскому институту в Лондоне свое исследование, проведенное в Калькутте.[6]
Изучение диэлектрических волноводов (таких как оптические волокна, см. Ниже) началось еще в 1920-х годах несколькими людьми, самыми известными из которых являются Рэлей, Зоммерфельд и Дебай.[7] Оптическое волокно стало привлекать особое внимание в 1960-х годах из-за его важности для индустрии связи.
Развитие радиосвязи первоначально происходило на более низких частотах, потому что их легче было распространять на большие расстояния. Длинные волны делали эти частоты непригодными для использования в полых металлических волноводах из-за того, что требовались трубы непрактично большого диаметра. Следовательно, исследования полых металлических волноводов застопорились, и работа лорда Рэлея была на время забыта, и другим пришлось заново открывать ее. Практические исследования, возобновленные в 1930-х гг. Джордж К. Саутворт в Bell Labs и Уилмер Л. Барроу в Массачусетский технологический институт. Саутворт сначала взял теорию из статей о волнах в диэлектрических стержнях, потому что работы лорда Рэлея были ему неизвестны. Это несколько ввело его в заблуждение; некоторые из его экспериментов потерпели неудачу, потому что он не знал о феномене частота среза волновода уже найден в работе лорда Рэлея. Серьезной теоретической работой занимались Джон Р. Карсон и Салли П. Мид. Эта работа привела к открытию, что для TE01 В кольцевом волноводе потери падают с частотой, и одно время это был серьезный соперник для формата для дальней связи.[8]
Важность радар в Вторая Мировая Война дала большой импульс исследованиям волноводов, по крайней мере, на Союзник сторона. В магнетрон, разработанная в 1940 г. Джон Рэндалл и Гарри Бут в Университете Бирмингема в Соединенном Королевстве, обеспечил хороший источник энергии и сделал возможным использование микроволновых радаров. Важнейший центр исследований США находился в Радиационная лаборатория (Rad Lab) в Массачусетский технологический институт но многие другие принимали участие в США и Великобритании, например, Учреждение телекоммуникационных исследований. Руководителем группы фундаментального развития Rad Lab был Эдвард Миллс Перселл. Его исследователи включали Джулиан Швингер, Натан Маркувиц, Кэрол Грей Монтгомери и Роберт Х. Дике. Большая часть работы Rad Lab была сосредоточена на поиске модели с сосредоточенными элементами волноводных структур, так что компоненты в волноводе могут быть проанализированы с помощью стандартной теории схем. Ганс Бете также некоторое время проработал в Rad Lab, но там он разработал свою теорию малой апертуры, которая оказалась важной для фильтры резонатора волновода, впервые разработанная в Rad Lab. Немецкая сторона, с другой стороны, в значительной степени игнорировала потенциал волноводов в радарах до самого конца войны. Настолько, что когда части радара сбитого британского самолета были отправлены в Сименс и Гальске для анализа, даже если они были признаны микроволновыми компонентами, их назначение не удалось определить.
В то время в Германии очень пренебрегали микроволновыми технологиями. Обычно считалось, что это бесполезно для радиоэлектронной борьбы, и тем, кто хотел провести исследовательскую работу в этой области, не разрешалось это делать.
— Х. Майер, вице-президент Siemens & Halske во время войны
Немецким ученым даже разрешили продолжать публично публиковать свои исследования в этой области, потому что они не считались важными.[9]
Сразу после Второй мировой войны волновод стал предпочтительной технологией в области СВЧ. Однако есть некоторые проблемы; он громоздкий, дорогой в производстве, а эффект частоты среза затрудняет производство широкополосных устройств. Ребристый волновод может увеличить полосу пропускания за пределы октавы, но лучшим решением является использование технологии, работающей в ТЕМ режим (то есть не волновод), такой как коаксиальный проводники, так как TEM не имеют частоты среза. Также может использоваться экранированный прямоугольный проводник, который имеет определенные производственные преимущества по сравнению с коаксиальным кабелем и может рассматриваться как предшественник планарных технологий (полоса и микрополоска). Тем не менее, планарные технологии начали набирать обороты с появлением печатных схем. Эти методы значительно дешевле, чем волноводные, и в значительной степени заняли свое место в большинстве диапазонов. Тем не менее, волновод по-прежнему пользуется популярностью в более высоких микроволновых диапазонах. Группа Ku вверх.[10]
Характеристики
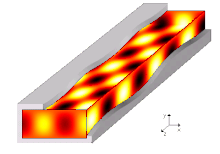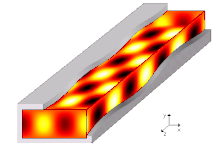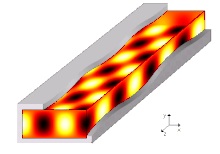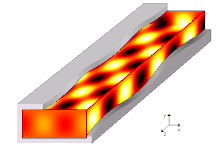
Режимы распространения и частоты среза
А режим распространения в волноводе - это одно из решений волновых уравнений, или, другими словами, форма волны.[7] Из-за ограничений граничные условия, существуют только ограниченные частоты и формы для волновой функции, которая может распространяться в волноводе. Самая низкая частота, на которой может распространяться определенная мода, - это частота среза этого режима. Режим с самой низкой частотой отсечки является основной модой волновода, а его частота отсечки - частотой отсечки волновода.
Режимы распространения рассчитываются путем решения Уравнение Гельмгольца наряду с набором граничных условий в зависимости от геометрической формы и материалов, ограничивающих область. Обычное предположение для бесконечно длинных однородных волноводов позволяет нам предположить распространяющуюся форму волны, то есть утверждая, что каждый компонент поля имеет известную зависимость от направления распространения (т. Е. ). В частности, общий подход состоит в том, чтобы сначала заменить все неизвестные изменяющиеся во времени неизвестные поля (предполагая для простоты описание полей в декартов компоненты) с их комплексом фазоры представление , достаточного для полного описания любого бесконечно длинного однотонального сигнала на частоте , (угловая частота ), и перепишем уравнение Гельмгольца и граничные условия соответственно. Затем каждое неизвестное поле вынуждено иметь форму вроде , где член представляет собой постоянную распространения (еще неизвестную) вдоль направления, вдоль которого волновод простирается на бесконечность. Уравнение Гельмгольца можно переписать так, чтобы оно соответствовало такой форме, и полученное равенство необходимо решить для и , что в конечном итоге дает уравнение на собственные значения для и соответствующая собственная функция для каждого решения первого.[11]
Постоянная распространения волноводной волны в целом сложна. Для случая без потерь постоянная распространения может принимать реальные или мнимые значения в зависимости от выбранного решения уравнения собственных значений и угловой частоты. . Когда является чисто реальным, мода называется "ниже пороговой", так как амплитуда векторов поля имеет тенденцию экспоненциально уменьшаться с распространением; воображаемый вместо этого представляет режимы, которые, как говорят, находятся «в распространении» или «выше порогового значения», поскольку комплексная амплитуда векторов не изменяется с .[12]
Согласование импеданса
В теория цепей, то сопротивление является обобщением электрическое сопротивление в случае переменный ток, и измеряется в Ом ().[7]Волновод в теории цепей описывается линия передачи имеющий длину и характеристическое сопротивление. Другими словами, импеданс показывает отношение напряжения к току компонента схемы (в данном случае волновода) во время распространения волны. Это описание волновода изначально предназначалось для переменного тока, но оно также подходит для электромагнитных и звуковых волн, так как волна и свойства материала (например, давление, плотность, диэлектрическая постоянная) правильно преобразованы в электрические термины (Текущий и импеданс, например).
Согласование импеданса важно, когда компоненты электрической цепи подключены (например, волновод к антенне): отношение импеданса определяет, какая часть волны передается вперед, а какая отражается. При подключении волновода к антенне обычно требуется полная передача, поэтому стараются согласовать их импедансы.
Коэффициент отражения можно рассчитать с помощью: , куда (Гамма) - коэффициент отражения (0 означает полное пропускание, 1 - полное отражение и 0,5 - отражение половины входящего напряжения), и - импеданс первой составляющей (из которой входит волна) и второй составляющей соответственно.
Несовпадение импеданса создает отраженную волну, которая, добавленная к приходящим волнам, создает стоячую волну. Несоответствие импеданса также можно количественно оценить с помощью коэффициент стоячей волны (КСВ или КСВ для напряжения), который связан с отношением импеданса и коэффициентом отражения посредством: , куда - минимальное и максимальное значения напряжения абсолютная величина, а VSWR - это коэффициент стоячей волны по напряжению, значение которого 1 означает полное пропускание без отражения и, следовательно, без стоячей волны, в то время как очень большие значения означают высокое отражение и характер стоячей волны.
Электромагнитные волноводы
Радиочастотные волноводы
Волноводы могут быть сконструированы так, чтобы переносить волны через широкую часть электромагнитный спектр, но особенно полезны в микроволновая печь и оптический частотные диапазоны. В зависимости от частоты они могут быть построены либо из проводящий или же диэлектрик материалы. Волноводы используются для передачи обоих мощность и коммуникационные сигналы.

Оптические волноводы
Волноводы, используемые на оптических частотах, обычно представляют собой диэлектрические волноводы, структуры, в которых диэлектрик материал с высоким диэлектрическая проницаемость, и, следовательно, высокий показатель преломления, окружен материалом с более низкой диэлектрической проницаемостью. Структура направляет оптические волны полное внутреннее отражение. Примером оптического волновода является оптоволокно.
Также используются другие типы оптических волноводов, в том числе фотонно-кристаллическое волокно, который направляет волны с помощью любого из нескольких различных механизмов. Направляющие в виде полой трубы с сильно отражающей внутренней поверхностью также использовались в качестве световые трубы для освещения. Внутренние поверхности могут быть из полированного металла или могут быть покрыты многослойной пленкой, которая направляет свет через Отражение Брэгга (это частный случай фотонно-кристаллического световода). Можно также использовать небольшие призмы вокруг трубы, которые отражают свет за счет полного внутреннего отражения [2]- такое ограничение неизбежно несовершенно, поскольку полное внутреннее отражение никогда не может по-настоящему направлять свет в пределах ниже-индексный сердечник (в случае призмы часть света просачивается по углам призмы).
Акустические волноводы
An акустический волновод физическая структура для направления звуковых волн. Канал для распространения звука также ведет себя как линия передачи. Канал содержит некоторую среду, например воздух, которая способствует распространению звука.
Математические волноводы
Волноводы - интересный объект исследования со строго математической точки зрения. Волновод (или трубка) определяется как тип граничного условия в волновом уравнении, при котором волновая функция должна быть равна нулю на границе и что допустимая область конечна во всех измерениях, кроме одного (бесконечно длинный цилиндр является примером .) Из этих общих условий можно получить большое количество интересных результатов. Оказывается, что любая трубка с выпуклостью (где ширина трубки увеличивается) допускает по крайней мере одно связанное состояние, которое существует внутри модовых промежутков. Частоты всех связанных состояний можно определить по короткому по времени импульсу. Это можно показать с помощью вариационных принципов. Интересный результат Джеффри Голдстоун и Роберт Джаффе [13] состоит в том, что любая трубка постоянной ширины с закруткой допускает связанное состояние.
Звуковой синтез
Звуковой синтез использует цифровые линии задержки в качестве вычислительных элементов для моделирования распространение волн в тюбиках духовые инструменты и вибрирующие струны из струнные инструменты.
Смотрите также
Рекомендации
- ^ Институт инженеров по электротехнике и электронике, «Стандартный словарь терминов по электротехнике и электронике IEEE»; 6-е изд. Нью-Йорк, штат Нью-Йорк, Институт инженеров по электротехнике и радиоэлектронике, c1997. IEEE Std 100-1996. ISBN 1-55937-833-6 [изд. Координационный комитет по стандартам 10, Термины и определения; Джейн Радац, (председатель)]
- ^ ОРИЕНТАЦИЯ С ПОМОЩЬЮ ДАЛЬНЕЙШИХ АКУСТИЧЕСКИХ СИГНАЛОВ У КИТОВ, Р. Пейн, Д. Уэбб, в Annals NY Acad. Наук, 188:110-41 (1971)
- ^ Дж. Р. Бейкер-Джарвис, "Измерения диэлектрической проницаемости линий передачи / отражения и короткого замыкания", NIST tech. нота 1341, июль 1990 г.
- ^ Н. В. Маклахлан, Теория и приложения функций Матье, с. 8 (1947) (перепечатано Dover: New York, 1964).
- ^ Теория звука, Дж. У. С. Рэлей, (1894)
- ^ Эмерсон, Д. Т. (1997). «Работа Джагадиса Чандры Боса: 100 лет исследований MM-волн». 1997 г., дайджест Международного симпозиума по микроволновому излучению IEEE MTT-S. Протоколы IEEE по теории и исследованиям микроволн. 45. С. 2267–2273. Bibcode:1997imsd.conf..553E. CiteSeerX 10.1.1.39.8748. Дои:10.1109 / MWSYM.1997.602853. ISBN 9780986488511. S2CID 9039614. перепечатано в сборнике Игоря Григорова, Под ред. Антентоп, Vol. 2, №3, с. 87–96.
- ^ а б c Передовая инженерная электромагнетизм В архиве 2009-05-14 на Wayback Machine, автор: К. А. Баланис, John Wiley & Sons (1989).
- ^ Олинер, стр. 544-548.
- ^ Олинер, стр. 548-554.
- Леви и Кон, стр. 1055, 1057
- ^ Олинер, стр. 556-557.
- Хан и Хван, стр. 21-7, 21-50.
- ^ Д. Позар, «Микроволновая техника», третье издание, Джон Вили и сыновья, 2005 г., глава 3.
- ^ Рамо, Саймон; Whinnery, John R .; Ван Дузер, Теодор (1994). Поля и волны в коммуникационной электронике. Нью-Йорк: Joh Wiley and Sons. С. 321–324. ISBN 978-0-471-58551-0.
- ^ *[1] Связанные состояния в скрученных трубках, Дж. Голдстоун, Р.Л. Джаффе, Департамент физики Массачусетского технологического института.
- Хан, C C; Hwang, Y, "Спутниковые антенны", in, Lo, Y T; Ли, SW, Справочник по антеннам: применение тома III, глава 21, Springer, 1993 ISBN 0442015941.
- Леви, Р; Кон, С. Б., «История исследований, проектирования и разработки микроволновых фильтров», IEEE Transactions: теория и методы микроволнового излучения, страницы 1055–1067, том 32, выпуск 9, 1984 г.
- Олинер, Артур А., «Эволюция электромагнитных волноводов: от полых металлических волноводов до микроволновых интегральных схем», глава 16 в, Sarkar и другие., История беспроводной связи, Wiley, 2006 г. ISBN 0471783013.
внешняя ссылка
| Искать волновод в Викисловаре, бесплатном словаре. |
| Викискладе есть медиафайлы по теме Волноводы. |
- Волновод Очень простое объяснение того, что такое волновод
- Основы волновода Несколько страниц с подробным руководством
- Электромагнитные волны и антенны: волноводы Софокл Дж. Орфанидис, факультет электротехники и вычислительной техники, Университет Рутгерса
- Связанные состояния в скрученных трубках, Дж. Голдстоун, Р.Л. Джаффе, Департамент физики Массачусетского технологического института