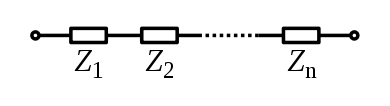WikiDer > Электрический импеданс

Статьи о
Электромагнетизм
Электричество Магнетизм История Учебники
Электростатика Электрический заряд Закон Кулона Дирижер Плотность заряда Разрешающая способность Электрический дипольный момент Электрическое поле Электрический потенциал Электрический поток / потенциальная энергия Электростатический разряд Закон Гаусса Индукция Изолятор Плотность поляризации Статичное электричество Трибоэлектричество
Магнитостатика Закон Ампера Закон Био – Савара Закон Гаусса для магнетизма Магнитное поле Магнитный поток Магнитный дипольный момент Магнитная проницаемость Магнитный скалярный потенциал Намагничивание Магнитодвижущая сила Правило правой руки
Электродинамика Закон силы Лоренца Электромагнитная индукция Закон Фарадея Закон Ленца Ток смещения Магнитный векторный потенциал Уравнения Максвелла Электромагнитное поле Электромагнитный импульс Электромагнитное излучение Тензор Максвелла Вектор Пойнтинга Потенциал Льенара – Вихерта Уравнения Ефименко Вихревой ток Уравнения Лондона Математические описания электромагнитного поля
Электрическая сеть Переменный ток Емкость Постоянный ток Электрический ток Электролиз Плотность тока Джоулевое нагревание Электродвижущая сила Импеданс Индуктивность Закон Ома Параллельная схема Сопротивление Резонансные полости Последовательная схема Напряжение Волноводы
Ковариантная формулировка Электромагнитный тензор (тензор энергии-импульса) Четырехтоковый Электромагнитный четырехпотенциальный
Ученые Ампер Биот Кулон Дэви Эйнштейн Фарадей Физо Гаусс Хевисайд Генри Герц Джоуль Ленц Лоренц Максвелл Ørsted Ом Ричи Savart Певица Тесла Вольта Вебер
v т е

В электротехника, электрический импеданс это мера сопротивления, которое цепь представляет текущий когда Напряжение применены.

Количественно импеданс двухполюсника элемент схемы - отношение комплексного представления синусоидальный напряжение между его выводами, до комплексного представления тока, протекающего через него.^[1] В общем, это зависит от частота синусоидального напряжения.

Импеданс расширяет понятие сопротивление к переменный ток (AC) цепи, и обладает как величиной, так и фаза, в отличие от сопротивления, которое имеет только величину. Когда цепь приводится в движение постоянный ток (DC) нет различия между импедансом и сопротивлением; последнее можно рассматривать как импеданс с нулевым угол фазы.

Импеданс - это комплексное число, с теми же единицами измерения, что и сопротивление, для которых Единица СИ это ом (ΩЕго символ обычно Z, и его можно представить, записав его величину и фазу в полярный форма |Z|∠θ. Однако, декартово представление комплексных чисел часто более эффективен для анализа схем.

Понятие импеданса полезно для выполнения анализа переменного тока электрические сети, поскольку он позволяет связывать синусоидальные напряжения и токи простым линейным законом. В нескольких порт сетей, двухполюсное определение импеданса неадекватно, но сложные напряжения на портах и ​​токи, протекающие через них, все еще остаются линейно связанный посредством матрица импеданса.^[2]

В взаимный импеданса допуск, чья SI единица Сименс, ранее назывался Мхо.

Инструменты, используемые для измерения электрического импеданса, называются анализаторы импеданса.

Введение

Период, термин сопротивление был придуман Оливер Хевисайд в июле 1886 г.^[3][4] Артур Кеннелли был первым, кто представил импеданс в виде комплексных чисел в 1893 году.^[5]

В дополнение к сопротивлению, которое наблюдается в цепях постоянного тока, полное сопротивление в цепях переменного тока включает эффекты индукции напряжений в проводниках из-за магнитные поля (индуктивность), а также электростатическое накопление заряда, вызванное напряжениями между проводниками (емкость). Импеданс, вызванный этими двумя эффектами, в совокупности называется реактивное сопротивление и формирует воображаемый часть комплексного импеданса, тогда как сопротивление формирует настоящий часть.

Импеданс определяется как частотная область отношение напряжения к току.^[6] Другими словами, это отношение напряжения к току для одного комплексная экспонента на определенной частоте ω.

Для входа синусоидального тока или напряжения полярная форма комплексного импеданса связывает амплитуду и фазу напряжения и тока. Особенно:

• Величина комплексного импеданса - это отношение амплитуды напряжения к амплитуде тока;
• Фаза комплексного импеданса - это сдвиг фазы на что ток отстает от напряжения.

Комплексный импеданс

Графическое представление плоскость комплексного импеданса

Импеданс двухконтактного элемента схемы представлен как сложный количество ${ displaystyle Z}$. В полярная форма удобно фиксирует как амплитудные, так и фазовые характеристики как

${ Displaystyle Z = | Z | е ^ {j arg (Z)}}$

где величина ${ displaystyle | Z |}$ представляет собой отношение амплитуды разности напряжений к амплитуде тока, а аргумент ${ Displaystyle arg (Z)}$ (обычно обозначается символом ${ displaystyle theta}$) дает разность фаз между напряжением и током. ${ displaystyle j}$ это мнимая единица, и используется вместо ${ displaystyle i}$ в этом контексте, чтобы избежать путаницы с символом электрический ток.

В Декартова форма, импеданс определяется как

${ Displaystyle Z = R + jX}$

где реальная часть импеданса это сопротивление ${ displaystyle R}$ и мнимая часть это реактивное сопротивление ${ displaystyle X}$.

Там, где необходимо добавить или вычесть импедансы, более удобна декартова форма; но когда количества умножаются или делятся, расчет становится проще, если используется полярная форма. Расчет схемы, такой как определение полного импеданса двух параллельных импедансов, может потребовать преобразования между формами несколько раз во время расчета. Преобразование между формами происходит по обычному правила преобразования комплексных чисел.

Комплексное напряжение и ток

Обобщенные импедансы в цепи могут быть обозначены тем же символом, что и резистор (US ANSI или DIN Euro), или маркированной рамкой.

Для упрощения расчетов синусоидальный Волны напряжения и тока обычно представляют как комплексные функции времени, обозначаемые как ${ displaystyle V}$ и ${ displaystyle I}$.^[7][8]

${ Displaystyle { begin {align} V & = | V | e ^ {j ( omega t + phi _ {V})}, I & = | I | e ^ {j ( omega t + phi _ { I})}. End {выравнивается}}}$

Импеданс биполярной цепи определяется как отношение этих величин:

${ displaystyle Z = { frac {V} {I}} = { frac {| V |} {| I |}} e ^ {j ( phi _ {V} - phi _ {I})} .}$

Следовательно, обозначая ${ displaystyle theta = phi _ {V} - phi _ {I}}$, у нас есть

${ displaystyle { begin {align} | V | & = | I || Z |, phi _ {V} & = phi _ {I} + theta. end {выравнивается}}}$

Уравнение амплитуды - это знакомый закон Ома, применяемый к амплитудам напряжения и тока, а второе уравнение определяет соотношение фаз.

Срок действия комплексного представления

Это представление с использованием комплексных экспонент можно оправдать, отметив, что (по Формула Эйлера):

${ displaystyle cos ( omega t + phi) = { frac {1} {2}} { Big [} e ^ {j ( omega t + phi)} + e ^ {- j ( omega t + phi)} { Big]}}$

Действительная синусоидальная функция, представляющая напряжение или ток, может быть разбита на две комплексные функции. По принципу суперпозиция, мы можем проанализировать поведение синусоиды в левой части, анализируя поведение двух сложных членов в правой части. Учитывая симметрию, нам нужно выполнить анализ только для одного правого члена. Результаты идентичны для другого. В конце любых вычислений мы можем вернуться к синусоидам с действительным знаком, отметив далее, что

${ Displaystyle соз ( омега т + фи) = ре { большой {} е ^ {дж ( омега т + фи)} { большой }}}$

Закон Ома

Источник переменного тока, подающий напряжение ${ displaystyle V}$через грузить ${ displaystyle Z}$, управляя током ${ displaystyle I}$

Значение электрического импеданса можно понять, подставив его в закон Ома.^[9][10]Предполагая, что двухконтактный элемент схемы с полным сопротивлением ${ displaystyle Z}$ управляется синусоидальным напряжением или током, как указано выше,

${ Displaystyle V = IZ = I | Z | е ^ {j arg (Z)}}$

Величина импеданса ${ displaystyle | Z |}$ действует так же, как сопротивление, давая падение амплитуды напряжения на импедансе ${ displaystyle Z}$ для данного тока ${ displaystyle I}$. В фазовый фактор говорит нам, что ток отстает от напряжения на фазу ${ Displaystyle тета ; = ; arg (Z)}$ (т.е. в область времени, текущий сигнал сдвигается ${ displaystyle { frac { theta} {2 pi}} T}$ позже относительно сигнала напряжения).

Подобно тому, как сопротивление распространяет закон Ома на цепи переменного тока, другие результаты анализа цепей постоянного тока, такие как деление напряжения, текущее деление, Теорема Тевенина и Теорема Нортона, также можно распространить на цепи переменного тока, заменив сопротивление импедансом.

Фазоры

Вектор представляет собой постоянное комплексное число, обычно выражаемое в экспоненциальной форме, представляющее комплексную амплитуду (величину и фазу) синусоидальной функции времени. Фазоры используются инженерами-электриками для упрощения вычислений с использованием синусоид, где они часто могут свести проблему дифференциального уравнения к алгебраической.

Импеданс элемента схемы может быть определен как отношение векторного напряжения на элементе к векторному току через элемент, что определяется относительными амплитудами и фазами напряжения и тока. Это идентично определению из Закон Ома приведенных выше, признавая, что факторы ${ displaystyle e ^ {j omega t}}$ Отмена.

Примеры устройств

Резистор

Фазовые углы в уравнениях для импеданса конденсаторов и катушек индуктивности показывают, что напряжение на конденсаторе лаги ток через него фазой ${ displaystyle pi / 2}$, а напряжение на катушке индуктивности ведет ток через него ${ displaystyle pi / 2}$. Одинаковые амплитуды напряжения и тока указывают на то, что величина импеданса равна единице.

Импеданс идеального резистор чисто реально и называется резистивный импеданс:

${ Displaystyle Z_ {R} = R}$

В этом случае формы сигналов напряжения и тока пропорциональны и синфазны.

Индуктор и конденсатор

Идеально индукторы и конденсаторы иметь чисто воображаемый реактивное сопротивление:

сопротивление катушек индуктивности увеличивается с увеличением частоты;

${ displaystyle Z_ {L} = j omega L}$

сопротивление конденсаторов уменьшается с увеличением частоты;

${ displaystyle Z_ {C} = { frac {1} {j omega C}}}$

В обоих случаях для приложенного синусоидального напряжения результирующий ток также синусоидальный, но квадратура, 90 градусов не совпадают по фазе с напряжением. Однако фазы имеют противоположные знаки: в индукторе ток равен отставание; в конденсаторе ток ведущий.

Обратите внимание на следующие тождества для воображаемой единицы и ее обратной величины:

${ displaystyle { begin {align} j & Equiv cos { left ({ frac { pi} {2}} right)} + j sin { left ({ frac { pi} {2 }} right)} Equiv e ^ {j { frac { pi} {2}}} { frac {1} {j}} Equiv -j & Equiv cos { left (- { frac { pi} {2}} right)} + j sin { left (- { frac { pi} {2}} right)} Equiv e ^ {j (- { frac { pi} {2}})} end {выровнен}}}$

Таким образом, уравнения импеданса индуктора и конденсатора можно переписать в полярной форме:

${ displaystyle { begin {align} Z_ {L} & = omega Le ^ {j { frac { pi} {2}}} Z_ {C} & = { frac {1} { omega C}} e ^ {j left (- { frac { pi} {2}} right)} end {align}}}$

Величина показывает изменение амплитуды напряжения для данной амплитуды тока через импеданс, тогда как экспоненциальные множители дают фазовое соотношение.

Получение импеданса конкретного устройства

Ниже приводится расчет импеданса для каждого из трех основных цепь элементы: резистор, конденсатор и катушка индуктивности. Хотя идею можно расширить, чтобы определить взаимосвязь между напряжением и током любого произвольного сигнал, эти выводы предполагают синусоидальный сигналы. Фактически, это применимо к любым произвольным периодическим сигналам, потому что они могут быть аппроксимированы как сумма синусоид через Анализ Фурье.

Резистор

Для резистора существует соотношение

${ displaystyle v _ { text {R}} left (t right) = {я _ { text {R}} left (t right)} R}$

который Закон Ома.

Считая сигнал напряжения

${ Displaystyle v _ { текст {R}} (t) = V_ {p} sin ( omega t)}$

это следует из того

${ displaystyle { frac {v _ { text {R}} left (t right)} {i _ { text {R}} left (t right)}} = { frac {V_ {p} sin ( omega t)} {I_ {p} sin left ( omega t right)}} = R}$

Это говорит о том, что отношение амплитуды переменного напряжения к переменный ток (AC) амплитуда на резисторе равна ${ displaystyle R}$, и что переменное напряжение опережает ток через резистор на 0 градусов.

Этот результат обычно выражается как

${ displaystyle Z _ { text {резистор}} = R}$

Конденсатор

Для конденсатора существует соотношение:

${ displaystyle i _ { text {C}} (t) = C { frac { operatorname {d} v _ { text {C}} (t)} { operatorname {d} t}}}$

Считая сигнал напряжения

${ displaystyle v _ { text {C}} (t) = V_ {p} e ^ {j omega t} ,}$

это следует из того

${ displaystyle { frac { operatorname {d} v _ { text {C}} (t)} { operatorname {d} t}} = j omega V_ {p} e ^ {j omega t}}$

и таким образом, как и раньше,

${ displaystyle Z _ { text {конденсатор}} = { frac {v _ { text {C}} left (t right)} {я _ { text {C}} left (t right)}} = {1 over j omega C}.}$

И наоборот, если ток в цепи предполагается синусоидальным, его комплексное представление будет

${ displaystyle i _ { text {C}} (t) = I_ {p} e ^ {j omega t} ,}$

затем интегрируя дифференциальное уравнение

${ displaystyle i _ { text {C}} (t) = C { frac { operatorname {d} v _ { text {C}} (t)} { operatorname {d} t}}}$

приводит к

${ displaystyle v_ {C} (t) = {1 over j omega C} I_ {p} e ^ {j omega t} + { text {Const}} = {1 over j omega C} i_ {C} (t) + { text {Const}}.}$

В Const Член представляет собой фиксированный потенциал смещения, наложенный на синусоидальный потенциал переменного тока, который не играет роли при анализе переменного тока. С этой целью этот член можно принять равным 0, следовательно, сопротивление

${ displaystyle Z _ { text {конденсатор}} = {1 over j omega C}.}$

Индуктор

Для индуктора имеем соотношение (из Закон Фарадея):

${ displaystyle v _ { text {L}} (t) = L { frac { operatorname {d} i _ { text {L}} (t)} { operatorname {d} t}}}$

На этот раз, учитывая, что текущий сигнал:

${ Displaystyle я _ { текст {L}} (т) = I_ {р} грех ( омега т)}$

это следует из того:

${ displaystyle { frac { operatorname {d} i _ { text {L}} (t)} { operatorname {d} t}} = omega I_ {p} cos left ( omega t right )}$

Этот результат обычно выражается в полярной форме как

${ displaystyle Z _ { text {индуктор}} = omega Le ^ {j { frac { pi} {2}}}}$

или, используя формулу Эйлера, как

${ displaystyle Z _ { text {индуктор}} = j omega L}$

Как и в случае с конденсаторами, эту формулу также можно вывести непосредственно из комплексных представлений напряжений и токов или допуская синусоидальное напряжение между двумя полюсами катушки индуктивности. В этом более позднем случае интегрирование приведенного выше дифференциального уравнения приводит к Const термин для тока, который представляет постоянное смещение постоянного тока, протекающее через катушку индуктивности. Это установлено на ноль, потому что анализ переменного тока с использованием импеданса в частотной области учитывает одну частоту за раз, а постоянный ток представляет в этом контексте отдельную частоту в ноль герц.

Обобщенный импеданс в s-плоскости

Импеданс определяется как jω может строго применяться только к цепям, которые управляются установившимся сигналом переменного тока. Понятие импеданса может быть расширено до цепи, запитанной любым произвольным сигналом, с помощью комплексная частота вместо того jω. Комплексная частота обозначается символом s и, как правило, является комплексным числом. Сигналы выражаются в терминах комплексной частоты с помощью Преобразование Лапласа из область времени выражение сигнала. Импеданс основных элементов схемы в этих более общих обозначениях следующий:

Элемент	Выражение импеданса
Резистор	${ Displaystyle R ,}$
Индуктор	${ Displaystyle sL ,}$
Конденсатор	${ displaystyle { frac {1} {sC}} ,}$

Для цепи постоянного тока это упрощает s = 0. Для установившегося синусоидального сигнала переменного тока s = jω.

Сопротивление против реактивного сопротивления

Сопротивление и реактивное сопротивление вместе определяют величину и фазу импеданса посредством следующих соотношений:

${ displaystyle { begin {align} | Z | & = { sqrt {ZZ ^ {*}}} = { sqrt {R ^ {2} + X ^ {2}}} theta & = arctan { left ({ frac {X} {R}} right)} end {align}}}$

Во многих приложениях относительная фаза напряжения и тока не критична, поэтому важна только величина импеданса.

Сопротивление

Сопротивление ${ displaystyle R}$ действительная часть импеданса; устройство с чисто резистивным импедансом не демонстрирует сдвига фаз между напряжением и током.

${ Displaystyle R = | Z | соз { theta} quad}$

Реактивность

Реактивность ${ displaystyle X}$ - мнимая часть импеданса; компонент с конечным реактивным сопротивлением вызывает фазовый сдвиг ${ displaystyle theta}$ между напряжением на нем и током через него.

${ Displaystyle X = | Z | грех { theta} quad}$

Чисто реактивный компонент отличается тем, что синусоидальное напряжение на компоненте находится в квадратуре с синусоидальным током, проходящим через компонент. Это означает, что компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь. Чистое реактивное сопротивление не рассеивает мощность.

Емкостное реактивное сопротивление

Конденсатор имеет чисто реактивный импеданс, равный обратно пропорциональный к сигналу частота. Конденсатор состоит из двух проводники разделены изолятор, также известный как диэлектрик.

${ Displaystyle X_ {C} = - ( omega C) ^ {- 1} = - (2 pi fC) ^ {- 1} quad}$

Знак минус указывает, что мнимая часть импеданса отрицательна.

На низких частотах конденсатор приближается к разомкнутой цепи, поэтому через него не течет ток.

Напряжение постоянного тока, приложенное к конденсатору, вызывает плата накапливаться на одной стороне; то электрическое поле за счет накопленного заряда является источником противодействия току. Когда потенциал связанный с зарядом точно уравновешивает приложенное напряжение, ток уходит в ноль.

Приведенный в действие источником переменного тока, конденсатор накапливает только ограниченный заряд, прежде чем разность потенциалов изменит знак и заряд рассеется. Чем выше частота, тем меньше накапливается заряда и меньше противодействие току.

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление ${ displaystyle X_ {L}}$ является пропорциональный к сигналу частота ${ displaystyle f}$ и индуктивность ${ displaystyle L}$.

${ Displaystyle X_ {L} = омега L = 2 pi fL quad}$

Индуктор состоит из спирального проводника. Закон Фарадея электромагнитной индукции возвращает ЭДС ${ displaystyle { mathcal {E}}}$ (напряжение противотока) из-за скорости изменения плотность магнитного потока ${ displaystyle B}$ через токовую петлю.

${ displaystyle { mathcal {E}} = - {{d Phi _ {B}} over dt} quad}$

Для индуктора, состоящего из катушки с ${ displaystyle N}$ циклы это дает:

${ displaystyle { mathcal {E}} = - N {d Phi _ {B} over dt} quad}$

Обратная ЭДС является источником противодействия току. Постоянная постоянный ток имеет нулевую скорость изменения и рассматривает катушку индуктивности как короткое замыкание (обычно изготавливается из материала с низким удельное сопротивление). An переменный ток имеет усредненную по времени скорость изменения, которая пропорциональна частоте, это вызывает увеличение индуктивного сопротивления с частотой.

Полное реактивное сопротивление

Полное реактивное сопротивление определяется как

${ displaystyle {X = X_ {L} + X_ {C}}}$ (Обратите внимание, что ${ displaystyle X_ {C}}$ отрицательный)

так что полный импеданс

${ Displaystyle Z = R + jX}$

Комбинирование импедансов

Общий импеданс многих простых сетей компонентов может быть рассчитан с использованием правил объединения импедансов последовательно и параллельно. Правила идентичны правилам комбинирования сопротивлений, за исключением того, что в целом числа сложные числа. Однако общий случай требует эквивалентные преобразования импеданса в дополнение к последовательному и параллельному.

Комбинация серий

Для компонентов, соединенных последовательно, ток через каждый элемент схемы одинаков; полный импеданс - это сумма импедансов компонентов.

${ displaystyle Z _ { text {eq}} = Z_ {1} + Z_ {2} + cdots + Z_ {n} quad}$

Или явно в реальном и воображаемом выражении:

${ displaystyle Z _ { text {eq}} = R + jX = (R_ {1} + R_ {2} + cdots + R_ {n}) + j (X_ {1} + X_ {2} + cdots + X_ {n}) quad}$

Параллельная комбинация

Для компонентов, соединенных параллельно, напряжение на каждом элементе схемы одинаковое; отношение токов через любые два элемента является обратной величиной их импедансов.

Следовательно, обратный полный импеданс является суммой обратных импедансов компонентов:

${ displaystyle { frac {1} {Z _ { text {eq}}}} = { frac {1} {Z_ {1}}} + { frac {1} {Z_ {2}}} + cdots + { frac {1} {Z_ {n}}}}$

или, когда n = 2:

${ displaystyle { frac {1} {Z _ { text {eq}}}} = { frac {1} {Z_ {1}}} + { frac {1} {Z_ {2}}} = { frac {Z_ {1} + Z_ {2}} {Z_ {1} Z_ {2}}}}$

${ displaystyle Z _ { text {eq}} = { frac {Z_ {1} Z_ {2}} {Z_ {1} + Z_ {2}}}}$

Эквивалентный импеданс ${ displaystyle Z _ { text {eq}}}$ можно рассчитать с точки зрения эквивалентного последовательного сопротивления ${ displaystyle R _ { text {eq}}}$ и реактивное сопротивление ${ displaystyle X _ { text {eq}}}$.^[11]

${ displaystyle { begin {align} Z _ { text {eq}} & = R _ { text {eq}} + jX _ { text {eq}} R _ { text {eq}} & = { гидроразрыв {(X_ {1} R_ {2} + X_ {2} R_ {1}) (X_ {1} + X_ {2}) + (R_ {1} R_ {2} -X_ {1} X_ {2 }) (R_ {1} + R_ {2})} {(R_ {1} + R_ {2}) ^ {2} + (X_ {1} + X_ {2}) ^ {2}}} X _ { text {eq}} & = { frac {(X_ {1} R_ {2} + X_ {2} R_ {1}) (R_ {1} + R_ {2}) - (R_ {1} R_ {2} -X_ {1} X_ {2}) (X_ {1} + X_ {2})} {(R_ {1} + R_ {2}) ^ {2} + (X_ {1} + X_ {2}) ^ {2}}} end {align}}}$

Измерение

Измерение импеданса устройств и линий передачи - практическая задача в радио технологии и другие области. Измерения импеданса можно проводить на одной частоте, или может представлять интерес изменение импеданса устройства в диапазоне частот. Импеданс может быть измерен или отображен непосредственно в омах, или могут отображаться другие значения, относящиеся к импедансу; например, в радиоантенна, то коэффициент стоячей волны или коэффициент отражения может быть более полезным, чем только импеданс. Измерение импеданса требует измерения величины напряжения и тока, а также разности фаз между ними. Импеданс часто измеряется «мостовые» методы, аналогично постоянному току Мост Уитстона; калиброванный эталонный импеданс регулируется для компенсации влияния импеданса тестируемого устройства. Измерение импеданса в силовых электронных устройствах может потребовать одновременного измерения и подачи питания на работающее устройство.

Импеданс устройства можно рассчитать сложным делением напряжения и тока. Импеданс устройства можно рассчитать, подав на устройство синусоидальное напряжение последовательно с резистором и измерив напряжение на резисторе и на устройстве. Выполнение этого измерения путем качания частот подаваемого сигнала позволяет получить фазу и величину импеданса.^[12]

Использование импульсной характеристики может использоваться в сочетании с быстрое преобразование Фурье (БПФ) для быстрого измерения электрического сопротивления различных электрических устройств.^[12]

В Измеритель LCR (Индуктивность (L), емкость (C) и сопротивление (R)) - это устройство, обычно используемое для измерения индуктивности, сопротивления и емкости компонента; исходя из этих значений, можно рассчитать импеданс на любой частоте.

пример

Рассмотрим LC бак цепь. Комплексный импеданс цепи равен

${ displaystyle Z ( omega) = {j omega L over 1- omega ^ {2} LC}.}$

Сразу видно, что значение ${ displaystyle {1 over | Z |}}$ минимально (фактически равняется 0 в данном случае) всякий раз, когда

${ displaystyle omega ^ {2} LC = 1.}$

Следовательно, угловая частота основного резонанса равна

${ displaystyle omega = {1 over { sqrt {LC}}}.}$

Переменный импеданс

В общем, ни импеданс, ни адмитанс не могут изменяться со временем, поскольку они определены для комплексных экспонент, в которых -∞ < т < +∞. Если комплексное экспоненциальное отношение напряжения к току изменяется во времени или по амплитуде, элемент схемы не может быть описан с использованием частотной области. Однако многие компоненты и системы (например, варикапсы которые используются в радио тюнеры) может иметь нелинейное или изменяющееся во времени отношение напряжения к току, которое кажется линейный инвариантный во времени (LTI) для небольших сигналов и для небольших окон наблюдения, поэтому их можно грубо описать как если бы они имели изменяющийся во времени импеданс. Это описание является приблизительным: при больших колебаниях сигнала или широких окнах наблюдения отношение напряжения к току не будет LTI и не может быть описано импедансом.

Смотрите также

• Анализ биоэлектрического импеданса
• Характеристический импеданс - Соотношение амплитуд напряжения и тока одиночной волны, распространяющейся по линии передачи
• Электрические характеристики динамических громкоговорителей
• Высокий импеданс
• Иммитанс
• Анализатор импеданса
• Мостовое сопротивление
• Кардиография импеданса
• Контроль импеданса
• Согласование импеданса
• Импедансная микробиология
• Конвертер отрицательного импеданса
• Расстояние сопротивления
• Импеданс линии передачи - Явление сигнала
• Универсальный диэлектрический отклик

использованная литература

внешние ссылки

• Объяснение импеданса
• Антенна Импеданс
• ECE 209: Обзор схем как систем LTI - Краткое объяснение анализа схем в области Лапласа; включает определение импеданса.