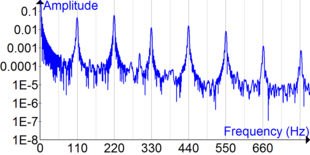
WikiDer > Акустический резонанс
Акустический резонанс это явление, в котором акустическая система усиливает звуковые волны, частота которых соответствует одной из собственных частот вибрации (его резонанс частоты).
Термин «акустический резонанс» иногда используется для сужения механический резонанс к частотному диапазону человеческого слуха, но поскольку акустика определяется в общих чертах относительно колебательных волн в веществе,[1] акустический резонанс может возникать на частотах вне диапазона человеческого слуха.
Акустически резонансный объект обычно имеет более одной резонансной частоты, особенно при гармоники сильнейшего резонанса. Он будет легко вибрировать на этих частотах и менее сильно вибрировать на других частотах. Он будет «выделять» свою резонансную частоту из сложного возбуждения, такого как импульсное или широкополосное шумовое возбуждение. Фактически, он отфильтровывает все частоты, кроме резонанса.
Акустический резонанс является важным фактором для производителей приборов, так как большинство акустических инструменты использовать резонаторы, например, строки и тело скрипка, длина трубки в флейта, и форма барабанной перепонки. Акустический резонанс также важен для слуха. Например, резонанс жесткого элемента конструкции, называемого базилярная мембрана в пределах улитка из внутреннее ухо позволяет волосковые клетки на мембране для обнаружения звука. (У млекопитающих мембрана имеет сужающиеся резонансы по всей длине, так что высокие частоты сосредоточены на одном конце, а низкие - на другом.)
Как и механический резонанс, акустический резонанс может привести к катастрофическому отказу вибратора. Классический пример этого: разбить бокал со звуком на точной резонансной частоте стекла.
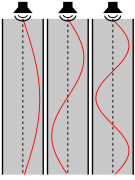
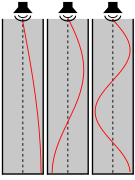
Вибрирующая струна
В музыкальных инструментах струны под натяжением, как в лютни, арфы, гитары, пианино, скрипки и так далее резонансные частоты напрямую связано с массой, длиной и натяжением струны. Длина волны, которая создаст первый резонанс на струне, равна удвоенной длине струны. Более высокие резонансы соответствуют длинам волн, которые являются целыми делениями фундаментальный длина волны. Соответствующие частоты связаны со скоростью v из волна, бегущая по струне по уравнению
куда L - длина строки (для строки, закрепленной на обоих концах) и п = 1, 2, 3...(Гармонический в трубе с открытым концом (то есть оба конца трубы открыты)). Скорость волны через струну или проволоку зависит от ее натяжения. Т и масса на единицу длины ρ:
Таким образом, частота связана со свойствами струны уравнением
куда Т это напряжение, ρ - масса на единицу длины, а м это общая масса.
Более высокое натяжение и меньшая длина увеличивают резонансные частоты. Когда струна возбуждается импульсной функцией (ощупывание пальцем или удар молотком), струна вибрирует на всех частотах, присутствующих в импульсе (импульсная функция теоретически содержит «все» частоты). Те частоты, которые не являются одним из резонансов, быстро отфильтровываются - они ослабляются - и все, что остается, - это гармонические колебания, которые мы слышим как музыкальную ноту.
Струнный резонанс в музыкальных инструментах
Струнный резонанс происходит на струнные инструменты. Струны или части струн могут резонировать на своих фундаментальный или же обертон частоты при звучании других струн. Например, струна A с частотой 440 Гц вызовет резонанс струны E с частотой 330 Гц, поскольку они имеют общий обертон 1320 Гц (3-й обертон A и 4-й обертон E).
Резонанс трубки воздуха
Резонанс трубки с воздухом зависит от длины трубки, ее формы и того, имеет ли она закрытые или открытые концы. Многие музыкальные инструменты напоминают трубки, которые конический или же цилиндрический (видеть сверлить). Труба, закрытая с одного конца и открытая с другого, называется остановился или же закрыто в то время как открыто труба открыта с обоих концов. Современный оркестр флейты ведут себя как открытые цилиндрические трубы; кларнеты ведут себя как закрытые цилиндрические трубы; и саксофоны, гобоев, и фаготы в виде закрытых конических труб,[2]в то время как большинство современных инструментов с язычком для губ (латунные инструменты) акустически аналогичны закрытым коническим трубам с некоторыми отклонениями (см. педальные тоны и ложные тонаКак и струны, колеблющиеся воздушные столбы в идеальных цилиндрических или конических трубах также имеют резонансы на гармониках, хотя есть некоторые отличия.
Цилиндров
Любой цилиндр резонирует на нескольких частотах, создавая несколько музыкальных нот. Самая низкая частота называется основной частотой или первой гармоникой. Цилиндры, используемые в качестве музыкальных инструментов, обычно открыты либо с обоих концов, как флейта, либо с одного конца, как некоторые органные трубы. Однако цилиндр, закрытый с обоих концов, также можно использовать для создания или визуализации звуковых волн, как в Труба Рубенса.
Резонансные свойства цилиндра можно понять, рассмотрев поведение звуковой волны в воздухе. Звук распространяется как продольная волна сжатия, заставляя молекулы воздуха двигаться вперед и назад вдоль направления движения. Внутри трубки образуется стоячая волна, длина которой зависит от длины трубки. В закрытом конце трубки молекулы воздуха не могут сильно двигаться, поэтому этот конец трубки представляет собой смещение. узел в стоячей волне. На открытом конце трубки молекулы воздуха могут свободно перемещаться, производя смещение пучность. Узлы смещения являются пучностями давления и наоборот.
Закрыто с обоих концов
В таблице ниже показаны волны смещения в цилиндре, закрытом с обоих концов. Обратите внимание, что молекулы воздуха около закрытых концов не могут двигаться, тогда как молекулы около центра трубы перемещаются свободно. В первой гармонике закрытая трубка содержит ровно половину стоячей волны (узел-пучность-узел).
| Частота | Заказ | Имя 1 | Название 2 | Название 3 | Волновое представление | Молекулярное представление |
|---|---|---|---|---|---|---|
| 1 · ж = 440 Гц | п = 1 | 1-я часть | основной тон | 1-я гармоника | 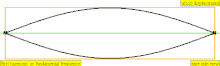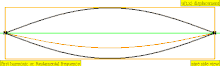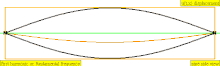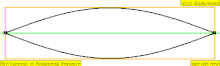 |  |
| 2 · f = 880 Гц | п = 2 | 2-й частичный | 1-й обертон | 2-я гармоника |  |  |
| 3 · ф = 1320 Гц | п = 3 | 3-й частичный | 2-й обертон | 3-я гармоника | 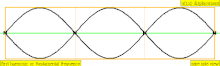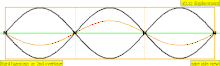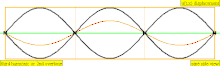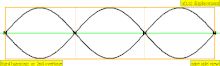 |  |
| 4 · ф = 1760 Гц | п = 4 | 4-я часть | 3-й обертон | 4-я гармоника | 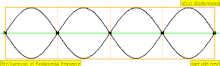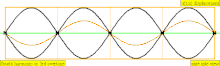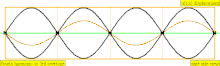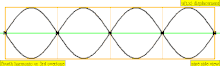 |  |
Открыты с обоих концов
В цилиндрах с открытыми обоими концами молекулы воздуха около конца свободно перемещаются в трубу и из нее. Это движение вызывает пучности смещения в стоячей волне. Узлы имеют тенденцию формироваться внутри цилиндра, вдали от концов. В первой гармонике открытая трубка содержит ровно половину стоячей волны (пучность-узел-пучность). Таким образом, гармоники открытого цилиндра рассчитываются так же, как гармоники закрытого / закрытого цилиндра.
Физика трубы, открытой с обоих концов, объясняется в Кабинет физики. Обратите внимание, что на схемах в этом справочнике показаны волны смещения, аналогичные показанным выше. Они резко контрастируют с волнами давления, показанными в конце данной статьи.
К раздувание На открытой трубке можно получить ноту, которая на октаву выше основной частоты или ноты трубки. Например, если основная нота открытой трубы - это C1, то при выдувании трубы за пределы трубы получается C2, которая на октаву выше C1.[3]
Открытые цилиндрические трубки резонируют примерно на частотах:
куда п положительное целое число (1, 2, 3 ...), представляющее узел резонанса, L - длина трубки и v это скорость звука в воздухе (что составляет примерно 343 метра в секунду [770 миль в час] при 20 ° C [68 ° F]).
Более точное уравнение с учетом конец исправления приведено ниже:
где d - диаметр резонансной трубки. Это уравнение компенсирует тот факт, что точная точка, в которой звуковая волна отражается от открытого конца, находится не идеально в концевой части трубки, а на небольшом расстоянии от нее.
Коэффициент отражения немного меньше 1; открытый конец не ведет себя как бесконечно малый акустический импеданс; скорее, он имеет конечное значение, называемое импедансом излучения, которое зависит от диаметра трубки, длины волны и типа отражающей панели, которая может присутствовать вокруг отверстия трубки.
Итак, когда n равно 1:
где v - скорость звука, L - длина резонансной трубки, d - диаметр трубки, f - резонансная частота звука, а λ - резонансная длина волны.
Закрыто с одного конца
При использовании в орган трубка, закрытая с одного конца, называется «остановленной трубой». Такие цилиндры имеют основную частоту, но их можно раздувать для воспроизведения более высоких частот или нот. Эти раздутые регистры можно настраивать, используя различные степени конусности. Закрытая трубка резонирует на той же основной частоте, что и открытая трубка, вдвое превышающая ее длину, с длиной волны, равной четырехкратной ее длине. В закрытой трубе смещение узел, или точка отсутствия вибрации, всегда появляется на закрытом конце, и если трубка резонирует, она будет иметь пучность, или направьте максимальную вибрацию на Фи острие (длина × 0,618) возле открытого конца.
К раздувание цилиндрическая закрытая трубка, можно получить купюру, которая находится примерно на двенадцатую часть выше основной ноты трубки или на пятую часть выше октава фундаментальной ноты. Например, если основной нотой закрытой трубы является C1, то при перепуске трубы получается G2, что на одну двенадцатую выше C1. В качестве альтернативы мы можем сказать, что G2 на одну пятую выше C2 - октавы выше C1. Регулировка конуса этого цилиндра для уменьшения конуса может настроить вторую гармонику или выдутую ноту близко к октавной позиции или 8-й.[4] Открытие небольшого "отверстия динамика" в Фи точка или общее положение «волна / узел» отменяет основную частоту и заставляет трубку резонировать на 12-й ступени выше основной. Этот метод используется в рекордер путем защемления откройте дорсальное отверстие для большого пальца. Перемещение этого маленького отверстия вверх, ближе к вокалу, сделает его «эхо-отверстием» (модификация записывающего устройства Dolmetsch), которое при открытии даст точную половину ноты выше основной. Примечание. Для точной настройки частоты половинной ноты требуется небольшая регулировка размера или диаметра.[3]
Закрытая трубка будет иметь приблизительные резонансы:
где «n» - нечетное число (1, 3, 5 ...). Этот тип лампы генерирует только нечетные гармоники, а его основная частота на октаву ниже, чем у открытого цилиндра (то есть вдвое ниже).
Более точное уравнение приведено ниже:
- .
Опять же, когда n равно 1:
где v - скорость звука, L - длина резонансной трубки, d - диаметр трубки, f - резонансная частота звука, а λ - резонансная длина волны.
Волна давления
На двух диаграммах ниже показаны первые три резонанса волны давления в цилиндрической трубе с пучностями на закрытом конце трубы. На схеме 1 трубка открыта с обоих концов. На диаграмме 2 он закрыт с одного конца. Горизонтальная ось - давление. Обратите внимание, что в этом случае открытый конец трубы является узлом давления, а закрытый конец - пучностью давления.
Шишки
Открытая коническая труба, т. Е. Имеющая форму усеченный конуса с двумя открытыми концами будет иметь резонансные частоты, примерно равные резонансным частотам открытой цилиндрической трубы такой же длины.
Резонансные частоты остановленной конической трубы - полного конуса или усеченного конуса с одним закрытым концом - удовлетворяют более сложному условию:
где волновое число k это
и Икс - расстояние от малого конца усеченной кости до вершины. Когда Икс мала, то есть когда конус почти готов, это становится
приводящие к резонансным частотам, примерно равным резонансным частотам открытого цилиндра, длина которого равна L + Икс. Другими словами, полная коническая труба ведет себя примерно как открытая цилиндрическая труба той же длины, и, в первую очередь, поведение не изменится, если весь конус заменен закрытой усеченной частью этого конуса.
Закрытый прямоугольный ящик
Звуковые волны в прямоугольной коробке включают такие примеры, как корпуса громкоговорителей и здания. Прямоугольное здание имеет резонансы, описанные как режимы комнаты. Для прямоугольного ящика резонансные частоты задаются выражением[5]
куда v это скорость звука, LИкс и Lу и Lz - это размеры коробки. , , и являются неотрицательными целыми числами, которые не могут быть все равны нулю.Если небольшой корпус громкоговорителя герметичен, частота достаточно низкая, а сжатие достаточно высокое, звуковое давление (уровень децибел) внутри коробки будет одинаковым в любом месте внутри коробки, это гидравлическое давление .
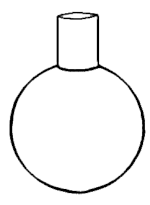
Резонанс сферы воздуха (вентилируемый)
Резонансная частота жесткой полости статического объема V0 с вырезанным звуковым отверстием площади А и длина L дается Резонанс Гельмгольца формула[6][7]
куда эквивалентная длина шеи с конец исправления
- для шеи без фланцев[8]
- для горловины с фланцем
Для сферической полости формула резонансной частоты принимает вид
куда
- D = диаметр сферы
- d = диаметр звукового отверстия
Для сферы только со звуковым отверстием, L= 0 и поверхность сферы действует как фланец, поэтому
В сухом воздухе при 20 ° C, с d и D в метрах, ж в Герц, это становится
Разбивание стекла звуком через резонанс
Это классическая демонстрация резонанса. Стекло имеет естественный резонанс - частоту, на которой стекло легко вибрирует. Следовательно, стекло должно перемещаться звуковой волной с этой частотой. Если сила звуковой волны, заставляющая стекло вибрировать, достаточно велика, размер вибрации станет настолько большим, что стекло расколется. Чтобы сделать это надежно для демонстрации науки, требуется практика и тщательный выбор стекла и динамика.[9]
В музыкальной композиции
Некоторые композиторы начали вносить резонанс в тему своих произведений. Элвин Люсьер использовал акустические инструменты и генераторы синусоидальных волн для исследования резонанса больших и малых объектов во многих своих композициях. Комплекс негармоничный частичные зыби в форме крещендо и декрещендо на тамтам или другой ударный инструмент, взаимодействующий с резонансами помещения в Джеймс Теннис Коан: Никогда не писал ноты для ударных. Полин Оливерос и Стюарт Демпстер регулярно выступать в больших реверберационный такие помещения, как 2 миллиона галлонов США (7600 м3) цистерна в Форт-Уорден, штат Вашингтон, в которой есть реверберация с 45-секундным затуханием. Музыкальная академия Мальмё композитора и композитора Кента Олофссона "Терпсикорд, пьеса для перкуссии и предварительно записанных звуков, [использует] резонансы акустических инструментов [для] формирования звуковых мостов к предварительно записанным электронным звукам, которые, в свою очередь, продлевают резонансы, преобразуя их в новые звуковые жесты ".[10]
Смотрите также
Рекомендации
- ^ Кинслер Л.Е., Фрей А.Р., Коппенс А.Б., Сандерс Дж. В., "Основы акустики", 3-е издание, ISBN 978-0-471-02933-5, Уайли, Нью-Йорк, 1982.
- ^ Вулф, Джо. «Акустика саксофона: введение». Университет Нового Южного Уэльса. Получено 1 января 2015.
- ^ а б Kool, Яап. Das Saxophon. J. J. Weber, Лейпциг. 1931. Перевод Лоуренс Гвоздз в 1987 г. обсуждаются «открытые» и «закрытые» трубки.
- ^ Валторны, струнные и гармония, Артур Х. Бенаде
- ^ Куттруфф, Генрих (2007). Акустика: введение. Тейлор и Фрэнсис. п. 170. ISBN 978-0-203-97089-8.
- ^ Вулф, Джо. «Резонанс Гельмгольца». Университет Нового Южного Уэльса. Получено 1 января 2015.
- ^ Грин, Чад А .; Арго IV, Теодор Ф .; Уилсон, Престон С. (2009). «Эксперимент с резонатором Гельмгольца для проекта Listen Up». Материалы совещаний по акустике. ASA: 025001. Дои:10.1121/1.3112687. Цитировать журнал требует
| журнал =(помощь) - ^ Райчел, Дэниел Р. (2006). Наука и применение акустики. Springer. С. 145–149. ISBN 978-0387-26062-4.
- ^ Центр акустических исследований. «Как разбить стакан звуком». Салфордский университет. Получено 17 января 2019.
- ^ Олофссон, Кент (4 февраля 2015 г.). «Резонансы и отклики». Дивергенция Пресс. Университет Хаддерсфилда Press (4). Дои:10.5920 / divp.2015.48.
- Недервен, Корнелис Йоханнес, Акустические аспекты деревянных духовых инструментов. Амстердам, Фриц Кнуф, 1969.
- Россинг, Томас Д., и Флетчер, Невилл Х., Принципы вибрации и звука. Нью-Йорк, Springer-Verlag, 1995.