WikiDer > Адаптивное кодирование Хаффмана
Адаптивное кодирование Хаффмана (также называемый Динамическое кодирование Хаффмана) является адаптивное кодирование техника, основанная на Кодирование Хаффмана. Это позволяет строить код по мере передачи символов, не имея начальных сведений о распределении источника, что позволяет кодировать за один проход и адаптировать к изменяющимся условиям в данных.
Преимущество однопроходной процедуры заключается в том, что источник можно кодировать в реальном времени, хотя он становится более чувствительным к ошибкам передачи, поскольку всего одна потеря разрушает весь код.
Алгоритмы
Существует ряд реализаций этого метода, наиболее заметными из которых являются: ФГК (Фаллер-Галлагер-Knuth) и Виттер алгоритм.
Алгоритм FGK
Это метод онлайн-кодирования, основанный на кодировании Хаффмана. Не имея начальных сведений о частотах появления, он позволяет динамически корректировать дерево Хаффмана по мере передачи данных. В дереве Хаффмана FGK специальный внешний узел, называемый 0-узел, используется для определения нового персонажа. То есть, всякий раз, когда встречаются новые данные, вывести путь к 0-узлу, за которым следуют данные. Для персонажа, пришедшего в прошлое, просто выведите путь к данным в текущем дереве Хаффмана. Самое главное, мы должны при необходимости скорректировать дерево FGK Huffman и, наконец, обновить частоту связанных узлов. По мере увеличения частоты данных родственная собственность дерева Хаффмана может быть сломано. По этой причине запускается регулировка. Это достигается последовательной заменой узлов, поддеревьев или того и другого. Узел данных заменяется узлом с наивысшим порядком той же частоты в дереве Хаффмана (или поддеревом с корнем в узле с наивысшим порядком). Все узлы-предки узла также должны обрабатываться таким же образом.
Поскольку алгоритм FGK имеет некоторые недостатки, связанные с заменой узлов и поддеревьев, Виттер предложил другой алгоритм для его улучшения.
Алгоритм Виттера
Некоторые важные термины и ограничения: -
- Неявная нумерация : Это просто означает, что узлы пронумерованы в порядке возрастания по уровню и слева направо. то есть узлы на нижнем уровне будут иметь низкий неявный номер по сравнению с узлами верхнего уровня, а узлы на том же уровне нумеруются в порядке возрастания слева направо.
- Инвариантный : Для каждого веса w все листы веса w предшествуют всем внутренним узлам, имеющим вес w.
- Блоки : Узлы одного веса и одного типа (то есть конечный узел или внутренний узел) образуют блок.
- Лидер : Узел с наибольшим номером в блоке.
Блоки связаны друг с другом по возрастанию их веса.
Листовой блок всегда предшествует внутреннему блоку того же веса, таким образом, сохраняется инвариант.
NYT (еще не переведено) является специальным узлом и используется для представления символов, которые 'еще не передан'.
алгоритм для добавления символа является leaf_to_increment: = NULL p: = указатель на листовой узел, содержащий следующий символ если (p - NYT) тогда Расширьте p, добавив двух дочерних элементов. Левый дочерний элемент становится новым NYT, а правый дочерний элемент - новым листовым узлом символа. п : = родительский элемент листового узла нового символа leaf_to_increment: = Правый дочерний элемент p еще Поменять местами p с лидером своего блока если (новый p - брат NYT) тогда leaf_to_increment: = p п : = родитель p пока (p ≠ NULL) делать Slide_And_Increment (p) если (leaf_to_increment! = NULL) тогда Slide_And_Increment (лист_до_инкремента)
функция Slide_And_Increment (p) является previous_p: = родительский элемент п если (p - внутренний узел) тогда Сдвиньте p в дереве выше, чем листовые узлы веса wt + 1, увеличьте вес п на 1 п : = previous_p еще Сдвиньте p в дереве выше внутренних узлов веса wt увеличить вес п на 1 п : = новый родитель п.
Кодер и декодер начинаются только с корневого узла, который имеет максимальное количество. Вначале это наш начальный узел NYT.
Когда мы передаем символ NYT, мы должны передать код для узла NYT, а затем для его общего кода.
Для каждого символа, который уже есть в дереве, нам нужно передать код только для его листового узла.
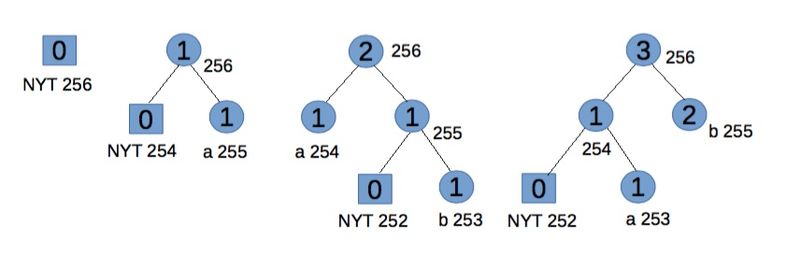
пример
Кодировка "abb" дает 01100001 001100010 11.
Шаг 1:
Начните с пустого дерева.
Для "a" передайте его двоичный код.
Шаг 2:
NYT порождает два дочерних узла: 254 и 255, оба с весом 0. Увеличьте вес для корневого и 255. Код для «a», связанный с узлом 255, равен 1.
Для «b» передайте 0 (для узла NYT), затем его двоичный код.
Шаг 3:
NYT порождает два дочерних узла: 252 для NYT и 253 для листового узла, оба с весом 0. Увеличьте веса для 253, 254 и корневого. Чтобы поддерживать инвариант Виттера, согласно которому все листья веса w предшествуют (в неявной нумерации) всем внутренним узлам веса w, ветвь, начинающаяся с узла 254, должна быть заменена (с точки зрения символов и весов, но не порядка номеров) узлом 255. Код для «b» - 11.
Для второго «б» передаем 11.
Для удобства объяснения этот шаг не совсем соответствует алгоритму Виттера,[1] но эффекты эквивалентны.
Шаг 4:
Перейдите к листовому узлу 253. Обратите внимание, что у нас есть два блока с весом 1. Узлы 253 и 254 - это один блок (состоящий из листьев), узел 255 - это другой блок (состоящий из внутренних узлов). Для узла 253 наибольшее число в его блоке - 254, поэтому поменяйте местами веса и символы узлов 253 и 254. Теперь узел 254 и ветвь, начинающаяся с узла 255, удовлетворяют условию SlideAndIncrement[1] и, следовательно, необходимо поменять местами. Наконец увеличьте вес узла 255 и 256.
Будущий код для «b» - 1, а для «a» теперь - 01, что отражает их частоту.
Рекомендации
- ^ а б «Адаптивное кодирование Хаффмана». Cs.duke.edu. Получено 2012-02-26.
- Оригинальная статья Виттера: J. S. Vitter, "Разработка и анализ динамических кодов Хаффмана", Журнал ACM, 34 (4), октябрь 1987 г., стр. 825–845.
- Дж. С. Виттер, "АЛГОРИТМ 673 Динамическое кодирование Хаффмана", Транзакции ACM в математическом программном обеспечении, 15 (2), июнь 1989 г., стр. 158–167. Также появляется в Сборнике алгоритмов ACM.
- Дональд Э. Кнут, «Динамическое кодирование Хаффмана», Журнал алгоритмов, 6 (2), 1985, стр. 163–180.
внешняя ссылка
 Эта статья включает материалы общественного достояния отNIST документ:Блэк, Пол Э. «адаптивное кодирование Хаффмана». Словарь алгоритмов и структур данных.
Эта статья включает материалы общественного достояния отNIST документ:Блэк, Пол Э. «адаптивное кодирование Хаффмана». Словарь алгоритмов и структур данных.- Сайт Калифорнийского университета Дэна Хиршберга
- Кардиффский университет Сайт доктора Дэвида Маршалла
- C реализация алгоритма Виттера
- Отличное описание от Duke University