WikiDer > Кодирование Шеннона – Фано – Элиаса

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален Найдите источники: «Кодирование Шеннона – Фано – Элиаса» – Новости · газеты · книги · ученый · JSTOR (Апрель 2016 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В теория информации, Кодирование Шеннона – Фано – Элиаса является предшественником арифметическое кодирование, в котором вероятности используются для определения кодовых слов.^[1]

Описание алгоритма

Учитывая дискретная случайная величина Икс из упорядоченный значения для кодирования, пусть ${ displaystyle p (x)}$ быть вероятностью для любого Икс в Икс. Определите функцию

${ displaystyle { bar {F}} (x) = sum _ {x_ {i}$

Алгоритм:

Для каждого Икс в Икс,

Позволять Z быть двоичным разложением ${ displaystyle { bar {F}} (х)}$.

Выберите длину кодировки Икс, ${ Displaystyle L (х)}$, чтобы быть целым числом ${ displaystyle left lceil log _ {2} { frac {1} {p (x)}} right rceil +1}$

Выберите кодировку Икс, ${ displaystyle code (x)}$, быть первым ${ Displaystyle L (х)}$ старшие биты после десятичной точки Z.

Пример

Пусть X = {A, B, C, D} с вероятностями p = {1/3, 1/4, 1/6, 1/4}.

Для

${ displaystyle { bar {F}} (A) = { frac {1} {2}} p (A) = { frac {1} {2}} cdot { frac {1} {3} } = 0,1666 ...}$

В двоичном формате Z (A) = 0.0010101010...

L (А) = ${ displaystyle left lceil log _ {2} { frac {1} { frac {1} {3}}} right rceil +1}$ = 3

код (A) - 001

Для B

${ displaystyle { bar {F}} (B) = p (A) + { frac {1} {2}} p (B) = { frac {1} {3}} + { frac {1 } {2}} cdot { frac {1} {4}} = 0,4583333 ...}$

В двоичном формате Z (B) = 0.01110101010101...

L (B) = ${ displaystyle left lceil log _ {2} { frac {1} { frac {1} {4}}} right rceil +1}$ = 3

код (B) - 011

Для C

${ displaystyle { bar {F}} (C) = p (A) + p (B) + { frac {1} {2}} p (C) = { frac {1} {3}} + { frac {1} {4}} + { frac {1} {2}} cdot { frac {1} {6}} = 0,66666 ...}$

В двоичном формате Z (C) = 0.101010101010...

L (C) = ${ displaystyle left lceil log _ {2} { frac {1} { frac {1} {6}}} right rceil +1}$ = 4

код (C) - 1010

Для D

${ displaystyle { bar {F}} (D) = p (A) + p (B) + p (C) + { frac {1} {2}} p (D) = { frac {1} {3}} + { frac {1} {4}} + { frac {1} {6}} + { frac {1} {2}} cdot { frac {1} {4}} = 0,875}$

В двоичном формате Z (D) = 0.111

L (D) = ${ displaystyle left lceil log _ {2} { frac {1} { frac {1} {4}}} right rceil +1}$ = 3

код (D) 111

Анализ алгоритмов

Код префикса

Кодирование Шеннона – Фано – Элиаса дает двоичный код префикса, позволяя прямое декодирование.

Пусть bcode (x) будет рациональным числом, образованным добавлением десятичной точки перед двоичным кодом. Например, если code (C) = 1010, то bcode (C) = 0.1010. Для всех x, если не существует y такого, что

${ displaystyle bcode (x) leq bcode (y)$

тогда все коды образуют префиксный код.

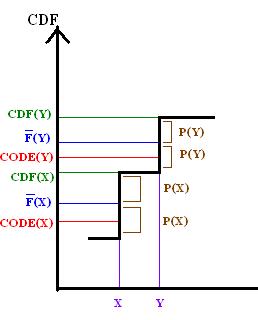
Сравнивая F с CDF X, это свойство может быть продемонстрировано графически для кодирования Шеннона – Фано – Элиаса.

По определению L следует, что

${ displaystyle 2 ^ {- L (x)} leq { frac {1} {2}} p (x)}$

И поскольку биты после L (y) усекаются от F (y) для формирования кода (y), из этого следует, что

${ displaystyle { bar {F}} (y) -bcode (y) leq 2 ^ {- L (y)}}$

таким образом, bcode (y) должен быть не меньше CDF (x).

Итак, приведенный выше график демонстрирует, что ${ displaystyle bcode (y) -bcode (x)> p (x) geq 2 ^ {- L (x)}}$, поэтому свойство префикса сохраняется.

Длина кода

Средняя длина кода ${ displaystyle LC (X) = sum _ {x epsilon X} p (x) L (x) = sum _ {x epsilon X} p (x) ( left lceil log _ {2} { frac {1} {p (x)}} right rceil +1)}$.
Таким образом, для H (X) Энтропия случайной величины X,

${ Displaystyle Н (Икс) +1 Leq LC (X) <Н (Х) +2}$

Шеннон Фано Элиас кодирует от 1 до 2 дополнительных бит на символ из X, чем энтропия, поэтому на практике этот код не используется.

Рекомендации