WikiDer > Автоволна
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Автоволны - самонесущие нелинейные волны в активные СМИ (то есть те, которые обеспечивают распределенные источники энергии). Этот термин обычно используется в процессах, в которых волны несут относительно низкую энергию, которая необходима для синхронизации или переключения активной среды.
Вступление
Актуальность и значимость
Автоволны (АВ) - распространенные аналоги автоколебание наблюдается в точечных системах. Примерами их являются волны горения, нервные импульсы, волны распределительного туннельного перехода (в полупроводниках) и т. Д. Автоволновые процессы (AWP) лежат в основе большинства процессов управления и передачи информации в биологических системах. (...) Интересной особенностью активных СМИ является то, что автоволновые структуры (AWS) может происходить в них. (...) Важность этой работы заключается в следующем
1. И AW, и AWS могут встречаться в системах любой физической природы. динамика из которых описывается уравнения (1).
2. Это новый тип динамические процессы которые приводят к макроскопическому линейному масштабу через локальные взаимодействия, каждое из которых не имеет линейного масштаба
3. AWS дает основу морфогенез в живых организмах (то есть в биологических системах).
4. Появление AWS - это новый механизм турбулентность в активных средах.Нажмите "Показать"чтобы увидеть исходный текст в (на русском)Автоволны (АВ) распределёнными аналогами автоколебаний в сосредоточенных системах. Их примерами волны горения, нервные импульсы, волны распределения туннельных переходов (в полупроводниках) и т.п. Автоволновые процессы (АВП) лежат в основе международных процессов управления и передачи информации в биологических системах. (...) Интересной особенностью активных сред является то, что в них возникать автоволновые структуры (АВС) (...) Важность АВС определяется следующим:
1. АВ и АВС могут осуществляться в системах любой физической природы, динамика которых описывается уравнениями вида (1).
2. Это новый тип динамических процессов, порождающих макроскопический линейный масштаб за счет локальных взаимодействий, каждый из которых линейным масштабом не обладает.
3. АВС существуют резервные морфогенеза в биологических системах.
4. Возникновение АВС - новый механизм. турбулентности в активных средах.— (1981), [B: 1]
В 1980 г. Советские ученые G.R. Иваницкий, В. Кринский, А. Заикин, ЯВЛЯЮСЬ. Жаботинский,[A: 1][A: 2][БИ 2] Б.П. Белоусов стали лауреатами высшей государственной награды СССР, Ленинская премия "за открытие нового класса автоволновых процессов и их изучение при нарушении устойчивости распределенных возбудимых систем.."
Краткая история исследований автоволн
Первыми, кто активно изучал автоколебания был академиком А.А. Андронов, и термин "автоколебания«в русскую терминологию ввел А.А. Андронов в 1928 году. Его последователи[примечание 1] из Лобачевского внес большой вклад в развитие теория автоволн.
Простейшие автоволновые уравнения, описывающие процессы горения, исследованы А.Н. Колмогоров,[A: 3] I.E. Петровский, Н.С. Пискунов в 1937г., а также Я.Б. Зельдович и Д.А. Франк-Каменецкий[A: 4] в 1938 г.
Классическая аксиоматическая модель с автоволнами в миокарде была опубликована в 1946 г. Норберт Винер и Артуро Розенблют.[A: 5]
В 1970-80 гг. Основные усилия по изучению автоволн были сосредоточены в Институт биологической физики из Академия наук СССР, расположенная в пригородном городке Пущино, под Москвой. Именно здесь под руководством В.И. Кринского такие всемирно известные ныне специалисты в области исследования автоволн, как А.В. Панфилов, И.Р. Ефимов, Р.Р. Алиев, К. Воспитывались и тренировались Агладзе, О.А. Морнев, М.А. Цыганов. В.В. Бикташев, Ю.Е. Елкин, А. Москаленко приобрел опыт теории автоволн также в Пущино, в соседнем Институт математических проблем биологии, под руководством Э.Э. Шнолля.
Термин «автоволновые процессы» для всех этих (и других) явлений был введен физиком СССР Р.В. Хохлов. Между этими автоволнами и идеями синергетики и самоорганизации существуют определенные и важные отношения.
— Васильев В.А. и др. (1987), [B: 3]
Период, термин "автоволны"было предложено, вероятно, по аналогии с ранее"автоколебания".
Практически сразу после Распад Советского СоюзаМногие из этих российских ученых уехали из родной страны для работы в зарубежных учреждениях, где они до сих пор продолжают исследования автоволн. В частности, Е.Р. Ефимов разрабатывает теория виртуального электрода,[A: 6] который описывает некоторые эффекты, возникающие во время дефибрилляция.
Среди других известных ученых, которые занимаются этим исследованием, - А.Н. Заикин, Э.Е. Шнолль (автоволны и бифуркационная память в системе свертывания крови);[A: 7][A: 8] А.Ю. Лоскутов (общая теория автоволн и динамический хаос в автоволнах);[B: 4] В.Г. Яхно (общая теория автоволн и связь автоволн с процессом мышления);[A: 9] К.И. Агладзе (автоволны в химических средах);[A: 10][A: 11] В. Н. Бикташев (общая теория автоволн, а также различные виды дрейфа автоволн);[A: 12][A: 13] О.А. Морнев (общая теория автоволн);[A: 14][A: 15] М.А. Цыганов (роль автоволны в динамике населения);[A: 16] Ю.Е. Елкин, А. Москаленко, (бифуркационная память в модели сердечной ткани).[A: 17][A: 18]
Огромная роль в исследовании автоволновых моделей сердечной ткани принадлежит Денис Ноубл и члены его команды из Оксфордский университет.
Основные определения
Одно из первых определений автоволн было следующим:
В настоящее время принято рассматривать автоволну как некоторый самоподдерживающийся волновой процесс в неравновесной среде, который остается неизменным при достаточно малых изменениях как начальных, так и граничных условий. (...) Математический аппарат для описания автоволн часто бывает уравнения диффузионного типа с активной нелинейностью.
Нажмите "Показать"чтобы увидеть исходный текст в (на русском)Под автоволнами принято сейчас понимать самоподдерживающийся волновой процесс в неравной среде, остающийся должен быть при малых изменениях как начальных, так и граничных условий. (...) Математическим аппаратом для описания автоволн всего всего экосистемного диффузионного типа с нелинейностью.— (1981), [B: 1]
В отличие от линейных волн - таких как звуковые волны, электромагнитные волны и другие, которые присущи консервативные системы и математически описывается линейным вторым порядком гиперболические уравнения (волновые уравнения), - динамика автоволна с точки зрения дифференциальные уравнения можно описать параболическое уравнение с нелинейным свободным членом особого вида.
Конкретная форма свободного члена чрезвычайно важно, потому что:
... все волновые процессы, порождаемые нелинейной динамикой точечной системы , который является автоколебательным или потенциально автоколебательным.
Нажмите "Показать"чтобы увидеть исходный текст в (на русском)все волновые процессы порождаются динамикой нелинейной точечной системы , которая является автоколебательной или первой автоколебательной.— (1981), [B: 1]
Обычно иметь форму -образная зависимость от .[требуется разъяснение] В этом смысле система уравнений, известная как модель Алиева – Панфилова,[A: 19] очень экзотический пример, потому что имеет в нем очень сложную форму двух пересекающихся парабол, кроме того, более пересеченных двумя прямыми линиями, что приводит к более выраженным нелинейным свойствам этой модели.
Автоволны является примером самоподдерживающегося волнового процесса в обширных нелинейных системах, содержащих распределенные источники энергии. Для простых автоволн верно, что период, длина волны, скорость распространения, амплитуда и некоторые другие характеристики автоволны определяются исключительно локальными свойствами среды. Однако в 21 веке исследователи начали обнаруживать все больше примеров автоволновых решений, когда нарушается «классический» принцип.
(См. Также общую информацию в литературе, например, в[B: 5][B: 3][B: 6][B: 4][A: 20][A: 17][A: 18][A: 7][A: 8]).
Самые простые примеры

Самая простая модель автоволны - это ряд домино, которые падают одно за другим, если вы уроните самое дальнее (так называемое "эффект домино"). Это пример волна переключения.
В качестве другого примера автоволн представьте, что вы стоите на поле и поджигаете траву. Пока температура ниже порога, трава не загорится. По достижении порог температура (температура самовоспламенения) горение начинается процесс с выделением тепла, достаточного для воспламенения ближайших участков. В результате получился фронт горения, который распространяется по полю. В таких случаях можно сказать, что возникла автоволна, что является одним из результатов самоорганизация в неравновесных термодинамических системах. Через некоторое время новая трава заменяет сгоревшую, и поле снова приобретает способность к возгоранию. Это пример волна возбуждения.
Среди автоволновых процессов также рассматривается множество других природных объектов: колебательные химические реакции в активных средах (например, Реакция Белоусова – Жаботинского), распространение импульсов возбуждения по нервным волокнам, волновая химическая сигнализация в колониях определенных микроорганизмов, автоволны в сегнетоэлектрик и полупроводник фильмы, демографические волны, распространение эпидемии и из гены, и многие другие явления.
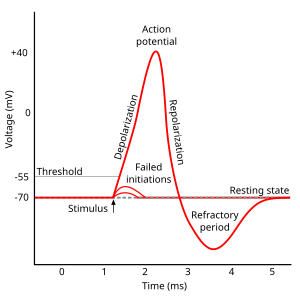
Нервные импульсы, служащие типичным примером автоволн в активной среде с восстановлением, были изучены еще в 1850 г. Герман фон Гельмгольц. Свойства нервных импульсов, характерные для простейших автоволновых решений (универсальная форма и амплитуда, не зависящие от начальных условий, аннигиляция при столкновениях), были установлены в 20-30-х годах прошлого века.
Рассмотрим двумерную активную среду, состоящую из элементов, каждый из которых может находиться в трех различных состояниях: покое, возбуждение и огнеупорность. При отсутствии внешнего воздействия элементы находятся в покое. В результате воздействия на него, когда концентрация активатора достигает порогового значения, элемент переходит в возбужденное состояние, приобретая способность возбуждать соседние элементы. Через некоторое время после возбуждения элемент переходит в тугоплавкое состояние, в котором он не может быть возбужден. Затем элемент возвращается в исходное состояние покоя, снова обретая способность переходить в возбужденное состояние.
Любая «классическая» волна возбуждения движется в возбудимой среде без затухания, сохраняя постоянную форму и амплитуду. По мере его прохождения потери энергии (рассеяние) полностью компенсируется подводом энергии от элементов активной среды. Передний фронт автоволны (переход из состояния покоя в состояние возбуждения) обычно очень мал: например, отношение длительности переднего фронта ко всей длительности импульса для образца миокарда составляет примерно 1: 330.
Уникальные возможности изучения автоволновых процессов в двух- и трехмерных активных средах с очень разной кинетикой предоставляют методы математического моделирования с использованием компьютеров. Для компьютерного моделирования автоволн используется обобщенная модель Винера – Розенблэта, а также большое количество других моделей, среди которых особое место занимает модель The Модель ФитцХью – Нагумо (простейшая модель активной среды и различные ее варианты) и Модель Ходжкина – Хаксли (нервный импульс). Также существует множество автоволновых моделей миокарда: Модель Билера – Рейтера, несколько моделей Noble (разработано Денис Ноубл), Модель Алиева – Панфилова., то Модель Фентона – Кармы, так далее.
Основные свойства автоволн
Также было доказано[A: 21] что простейшие автоволновые режимы должны быть общими для каждой системы дифференциальных уравнений любой сложности, описывающей конкретную активную среду, потому что такая система может быть упрощена до двух дифференциальных уравнений.
Основные известные автоволновые объекты
Прежде всего, мы должны заметить, что элементы активной среды могут быть, по крайней мере, трех очень разных типов; это увлекательный, возбудимый и спусковой крючок (или же бистабильный) режимы. Соответственно, существует три типа однородных активных сред, состоящих из этих элементов.
Бистабильный элемент имеет два устойчивых стационарных состояния, переходы между которыми происходят, когда внешнее воздействие превышает определенный порог. В средствах массовой информации таких элементов, волны переключения возникают, которые переводят среду из одного состояния в другое. Например, классический случай такой переключающейся автоволны - возможно, простейшее явление автоволны - это падающие домино (пример уже приводился). Другой простой пример бистабильной среды - горящая бумага: волна переключения распространяется в виде пламени, переводя бумагу из нормального состояния в пепел.
Возбудимый элемент имеет только одно устойчивое стационарное состояние. Внешнее воздействие на пороговом уровне может вывести такой элемент из его стационарного состояния и выполнить эволюцию, прежде чем элемент снова вернется в свое стационарное состояние. Во время такой эволюции активный элемент может воздействовать на соседние элементы и, в свою очередь, вывести их из стационарного состояния. В результате волна возбуждения размножается в этой среде. Это наиболее распространенная форма автоволн в биологических средах, таких как нервная ткань или миокард.
Автоколебательный элемент не имеет стационарных состояний и постоянно совершает устойчивые колебания фиксированной формы, амплитуды и частоты. Внешнее воздействие может нарушить эти колебания. После некоторого времени релаксации все их характеристики, кроме фазы, возвращаются к своему стабильному значению, но фазу можно изменить. В результате фазовые волны распространение в среде таких элементов. Такие фазовые волны можно наблюдать в электрогирляндах или в определенных химических средах. Примером автоколебательной среды является узел СА в сердце, в котором спонтанно возникают импульсы возбуждения.
На фазовом портрете основной системы уравнений, описывающей активную среду (см. Рис.), Хорошо видно, что существенное различие между этими тремя типами поведения активной среды обусловлено количеством и положением ее особых точек . Наблюдаемые в действительности автоволны по форме могут быть очень похожи друг на друга, поэтому определить тип элемента только по форме возбуждающего импульса может быть сложно.
Кроме того, автоволновые явления, которые можно наблюдать и исследовать, во многом зависят от геометрических и топологических особенностей активной среды.
Одномерные автоволны
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
К одномерным случаям относятся распространение автоволны в кабеле и ее распространение в кольце, причем последняя мода рассматривается как предельный случай вращающейся волны в двумерной активной среде, а первый случай рассматривается как распространение автоволны в кольце. с нулевой кривизной (т.е. с бесконечным радиусом).
Двумерные автоволны
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |

Известен ряд источников автоволн в двумерных активных средах. Таким образом, различают как минимум пять типов повторного входа,[заметка 2] которые бегать по кольцу, спиральная волна, ревербератор (т.е. двумерный автоволновой вихрь) и фибрилляция. В литературе выделяют два типа источников концентрические автоволны в 2D активных средах; это кардиостимуляторы и ведущие центры. Оба ведущие центры и ревербераторы интересны тем, что они не привязаны к структуре среды и могут появляться и исчезать в разных ее частях. Области повышенной автоматизации также могут быть примером источников автоволн. Сейчас известны три различных типа повышенной автоматизации:[B: 7]
- индуцированный автоматизм
- триггерный автоматизм с механизмом ранней постдеполяризации
- триггерный автоматизм с механизмом поздней постдеполяризации.
Смотрите также подробности в статье вращающиеся автоволны, который может выглядеть как спиральная волна или же автоволновый ревербератор.
Явления бифуркационная память наблюдались в поведении автоволнового ревербератора в Модель Алиева – Панфилова..[A: 17]
Трехмерные автоволны
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Примеры автоволновых процессов в природе
Автоволновый режим кипения
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Автоволны в химических растворах
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Примером химической реакции, которая при определенных обстоятельствах может вызвать автоволну, является Реакция Белоусова – Жаботинского.[A: 1][A: 2][БИ 2][B: 8][A: 24]
Автоволновые модели биологических тканей
Автоволновые модели сетчатки
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Автоволновые модели нервных волокон
Главный элемент на странице »Модель Ходжкина – Хаксли"
Автоволновые модели миокарда
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Классическая модель Винера — Розенблета,[A: 5] который, соответственно, разработан Норберт Винер и Артуро Розенблют.
Среди других примеров можно назвать следующие: FitxHue-Nagumo, модель Биллера-Рейтера.[A: 22][A: 25]
Основная статья планируется разместить на специальной странице »Автоволновые модели миокарда"
Автоволны в системе свертывания крови
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Автоволны населения
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Март 2013 г.) |
Коллективные амебы Dictyostelium discoideum при достаточном питании живут как одноклеточные организмы. Однако во время голода они ползают вместе, образуя многоклеточный организм, что позже дает споры которые могут выжить в неблагоприятных условиях. Было обнаружено, что движение амеб контролируется распределением некоторого вещества, морфоген лагерь, в окружающей среде. Такие клетки амебы синтезируют и накапливают молекулы цАМФ, а затем они способны «выпустить» этот резерв в окружающую среду, если в ней концентрация цАМФ увеличена. Высвободившееся количество цАМФ диффундирует через окружающую среду и заставляет следующие клеточные амебы «вступать в действие», выбрасывая свою часть морфогена. В результате автоволна высокой концентрации цАМФ распространяется по окружающей среде. После прохождения волны «разряженные» клетки снова начинают накапливать новую порцию цАМФ за счет синтеза, и через некоторое время они снова могут «включиться». Таким образом, популяция коллективные амебы типичный пример активная среда.
Нажмите "Показать"чтобы увидеть исходный текст в (на русском)Коллективные амёбы Dictyostelium discoideum при наличии достаточного питания в виде одноклеточных организмов. Однако при голодании они сползаются и образуют ru: Многоклеточный организм, который даёт ru: споры, способные пережить неблагоприятные условия. Установлено, что движение амёб управляется распределением по среднему веществу - морфогена цАМФ. Клетки амёб синтезируют и накапливают в себе молекулы цАМФ и «высвободить» его запас в глобальном будущем, если способность цАМФ в ней повысилась. Освободившееся количество цАМФ распространяется за счет диффузии по среде и заставляет следующие клетки амёб «сработать», выбросив свою порцию морфогена. В результате по распространению автоволна - повышенная повышенная цАМФ. После прохождения волны «разрядившиеся» клетки начинают накапливать за счёт импульсную порцию цАМФ и по прошествии некоторого времени способны «срабатывать» вновь. Таким образом, популяция коллективных амёб служит типичным примером средней среды.— Кринский и Михайлов, (1984)[B: 5]
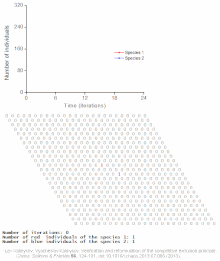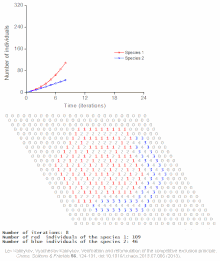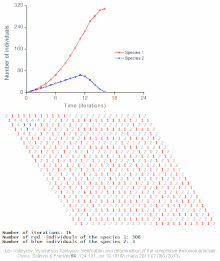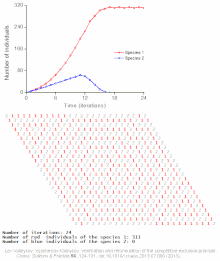
Примеры индивидуальных моделей популяционных автоволн
Смотрите также
Примечания
- ^ Например, это просто Почетный гражданин г. Нижний Новгород и заслуженный деятель науки РСФСР M.T. Грехова который был редактором книги «Автоволновые процессы в системах с диффузией» (1981) - см. Список литературы
- ^ Теперь хорошо известна печальная роль повторного входа как причины различных сердечных аритмий. Базовая схема повторного входа была предложена еще в 1914 г. и получена при исследовании изолированных колец сердечной ткани (GR Mines - Trans.R.Soc.Can., 1914, 8, 43). Т. Льюис и др. Продемонстрировали в 1921 году, что трепетание предсердий может быть обусловлено циркуляцией волны возбуждения вниз по правому и вверх по левому предсердию (Heart, 1921, 8, 361). Этот факт был снова подтвержден экспериментально в середине 20 века К. Э. Кабрерой и Д. Соли-Полларесом (Arch. Inst. Cardiol. Mex., 1947, 17,850). Существенная роль повторного входа как патогенетического механизма суправентрикулярная тахикардия был предложен в 1928 г. Ф. О. Шмидтом и Дж. Эрлангером (Am. J. Physiol. 1928-1929, 87, 326). Он также отвечает за многие типы желудочковой тахикардии и фибрилляции желудочков.
Рекомендации
- Книги
- ^ а б c Грехова, М. Т., изд. (1981). Автоволновые процессы в системе с диффузией [Автоволновые процессы в системах с диффузией] (на русском). Горький: Институт прикладной математики АН СССР. п. 287.
- ^ а б Жаботинский, А. М. Концентрационные автоколебания [Автоколебания концентрации] (на русском). М .: Наука.
- ^ а б Васильев, В. А .; Романовский, Ю. М .; Чернавский, Д. С .; Яхно, В. Г. (1987). Автоволновые процессы в кинетических системах. Пространственная и временная самоорганизация в физике, химии, биологии и медицине. Берлин: Springer, Нидерланды. Дои:10.1007/978-94-009-3751-2. ISBN 978-94-010-8172-6.
- ^ а б Лоскутов, А .; Михайлов, А. (1995). Основы синергетики II. Сложные шаблоны. Берлин: Springer.
- ^ а б Кринский, В. И .; Михайлов, А. С. (1984). Автоволны [Автоволны] (на русском). Москва: Знание.
- ^ Прохоров, А. М., изд. (1988). Физическая энциклопедия [Энциклопедия физики] (на русском). 1. М .: Советская энциклопедия.
- ^ Елькин, Ю.Е .; Москаленко, А.В. (2009). "Базовые механизмы аритмий сердца" [Основные механизмы сердечных аритмий]. В Ардашеве проф. СРЕДНИЙ. (ред.). Клиническая аритмология [Клиническая аритмология] (на русском). Москва: МедПрактика. п. 1220. ISBN 978-5-98803-198-7.
- ^ Филд, R.J .; Бургер, М., ред. (1985). Колебания и бегущие волны в химических системах. John Wiley and Sons, Inc.
- Статьи
- ^ а б Заикин, А. Н .; Жаботинский, А. М. (1970). «Распространение волны концентрации в двумерной жидкофазной автоколебательной системе». Природа. 225 (5232): 535–537. Дои:10.1038 / 225535b0. PMID 16056595.
- ^ а б Жаботинский, А. М .; Заикин, А. Н. (1973). «Автоволновые процессы в распределенной химической системе». Журнал теоретической биологии. 40 (1): 45–56. Дои:10.1016/0022-5193(73)90164-1. ISSN 0022-5193. PMID 4723554.
- ^ Колмогоров, А .; и другие. (1937). «Изучение уравнения диффузии, которое связано с ростом качества материи и его применение к биологической проблеме». Вестник МГУ по математике. 1: 1–26.
- ^ Зельдович, Ю. Б .; Франк-Каменецкий, Д. А. (1938). "(статья)". Acta Physicochimica U.S.S.R. 9: 341–.
- ^ а б Wiener, N .; Розенблют, А. (1946). «Математическая постановка задачи о проведении импульсов в сети связанных возбудимых элементов, в частности, в сердечной мышце». Archivos del Instituto de Cardiología de México. 16 (3–4): 205–265.
- ^ Самбелашвили, А. Т .; Никольский, В. П .; Ефимов И. Р. (2004). «Теория виртуального электрода объясняет повышение порога стимуляции, вызванное повреждением сердечной ткани». Американский журнал физиологии. Сердце и физиология кровообращения. 286 (6): H2183 – H2194. Дои:10.1152 / ajpheart.00637.2003.
- ^ а б c Атауллаханов Ф И; Зарницына, В I; Кондратович А Ю; Лобанова Э.С. Сарбаш, В I (2002). «Новый класс останавливающих самоподдерживающихся волн: фактор, определяющий пространственную динамику свертывания крови». Успехи физики. 45 (6): 619–636. Дои:10.3367 / UFNr.0172.200206c.0671. ISSN 0042-1294.
- ^ а б c Атауллаханов Ф И; Лобанова Э.С. Морозова, О Л; Шноль, Э Э; Ермакова, Е А; Бутилин, А А; Заикин А Н (2007). «Сложные режимы распространения возбуждения и самоорганизации в модели свертывания крови». Успехи физики. 50: 79–94. Дои:10.3367 / УФН.0177.200701д.0087. ISSN 0042-1294.
- ^ Васильев В А; Романовский Ю М; Яхно, В Г (1979). «Автоволновые процессы в распределенных кинетических системах». Успехи физики. 22: 615–639. Дои:10.3367 / UFNr.0128.197908c.0625.
- ^ Агладзе, К.И .; Кринский, В. (1982). «Многорукие вихри в активной химической среде». Природа. 296 (5856): 424–426. Дои:10.1038 / 296424a0.
- ^ Агладзе, К.И .; Кринский, В.И .; Перцов, А. (1984). «Хаос в невозмущенной реакции Белоусова-Жаботинского вызван взаимодействием волн и стационарных диссипативных структур». Природа. 308 (5962): 834–835. Дои:10.1038 / 308834a0.
- ^ а б Бикташев, В. Н .; Холден, А. В .; Чжан, Х. (1994). «Напряжение организующих нитей спиральных волн». Философские труды Королевского общества A: математические, физические и инженерные науки. 347 (1685): 611–630. Дои:10.1098 / Рста.1994.0070.
- ^ а б Бикташев, В. Н .; Холден, А. В. (1995). «Резонансный дрейф автоволновых вихрей в двух измерениях и влияние границ и неоднородностей». Хаос, солитоны и фракталы. 5 (3–4): 575–622. Дои:10.1016 / 0960-0779 (93) E0044-C. ISSN 0960-0779.
- ^ Асланиди, О. В .; Морнев, О.А. (1997). «Можно ли отразить встречные нервные импульсы?». Журнал экспериментальной и теоретической физики Letters. Наука / Интерпериодика. 65 (7): 579–585. Дои:10.1134/1.567398. ISSN 0021-3640.
- ^ Морнев, О. А. (2004). «Преломление автоволн: правило касательной». Журнал экспериментальной и теоретической физики Letters. Наука / Интерпериодика. 80 (12): 721–724. Дои:10.1134/1.1868793. ISSN 0021-3640.
- ^ Агладзе, К .; Будрене, Л .; Иваницкий, Г .; Кринский, В .; Шахбазян, В .; Цыганов, М. (1993). «Волновые механизмы формирования паттерна в микробной популяции». Труды Королевского общества B: биологические науки. 253 (1337): 131–135. Дои:10.1098 / rspb.1993.0092. PMID 8397413.
- ^ а б c Елкин, Ю. E .; Москаленко, А.В .; Стармер, Ч.Ф. (2007). «Самопроизвольная остановка дрейфа спиральной волны в однородных возбудимых средах». Математическая биология и биоинформатика. 2 (1): 1–9. ISSN 1994-6538.
- ^ а б Москаленко, А. В .; Елкин, Ю. Э. (2009). «Шнурок: новый тип поведения спиральной волны». Хаос, солитоны и фракталы. 40 (1): 426–431. Дои:10.1016 / j.chaos.2007.07.081. ISSN 0960-0779.
- ^ Алиев, Р .; Панфилов, А. (1996). «Простая двухпараметрическая модель возбуждения сердца». Хаос, солитоны и фракталы. 7 (3): 293–301. CiteSeerX 10.1.1.52.4271. Дои:10.1016/0960-0779(95)00089-5. ISSN 0960-0779.
- ^ Елькин, Ю. Е. (2006). «Автоволновые процессы» Автоволновые процессы [Автоволновые процессы]. Математическая биология и биоинформатика (журнал). 1 (1): 27–40. Дои:10.17537/2006.1.27. ISSN 1994-6538.
- ^ Кринский, В. И .; Кокоз, Ю. М. (1973). «Анализ уравнения возбудимых мембран III. Мембрана Пуркинье. Сведение уравнения Нобла к системе второго порядка. Биофизика (журнал) (на русском языке). 18 (6): 1067–1073. ISSN 0006-3029.
- ^ а б Уинфри, А. (1991). "Разновидности поведения спиральной волны: экспериментальный подход к теории возбудимых сред". Хаос. 1 (3): 303–334. Дои:10.1063/1.165844. ISSN 1054-1500. PMID 12779929.
- ^ Кинер, Дж. П. (1988). «Динамика трехмерных спиральных волн в возбудимых средах». Physica D. 31 (2): 269–276. Дои:10.1016/0167-2789(88)90080-2. ISSN 0167-2789.
- ^ Манелис, Георгий Б; и другие. (2012). «Автоволновые процессы при фильтрационном горении в противоточных системах». Российские химические обзоры. 81 (9): 855–. Дои:10.1070 / RC2012v081n09ABEH004279. ISSN 1468-4837.
- ^ Ефимов И.Р .; Кринский, В. И .; Джалифе, Дж. (1995). «Динамика вращающихся вихрей в модели сердечной ткани Билера-Рейтера». Хаос, солитоны и фракталы. 5 (3/4): 513–526. Дои:10.1016 / 0960-0779 (95) 95761-Ф. ISSN 0960-0779.
внешняя ссылка
- Несколько простых классических моделей автоволн (JS + WebGL), который можно запустить прямо в вашем браузере; разработал Евгений Демидов.