WikiDer > Волна
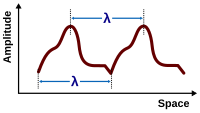
В физика, математика, и связанные поля, a волна является распространяющимся динамическим возмущением (отклонением от равновесия) одной или нескольких величин, иногда описываемым волновое уравнение. В физических волнах не менее двух поле количества в волновой среде. Волны могут быть периодическими, и в этом случае эти величины многократно колеблются вокруг равновесие (отдых) значение в некоторых частота. Когда вся форма волны движется в одном направлении, это называется бегущая волна; напротив, пара наложенный периодические волны, бегущие в противоположных направлениях, создают стоячая волна. В стоячей волне амплитуда колебаний имеет нулевые значения в некоторых положениях, где амплитуда волны кажется меньшей или даже нулевой.
Типы волн, наиболее часто изучаемые в классической физике: механический и электромагнитный. В механической волне стресс и напряжение поля колеблются около механического равновесия. Механическая волна - это локальная деформация (деформация) в некоторой физической среде, которая распространяется от частицы к частице, создавая локальные подчеркивает которые вызывают напряжение и в соседних частицах. Например, звук волны - это вариации местного давление и движение частиц которые распространяются через среду. Другие примеры механических волн: сейсмические волны, гравитационные волны, поверхностные волны, колебания струны (стоячие волны) и вихри[сомнительный ]. В электромагнитной волне (такой как свет) энергия обменивается между электрическим и магнитным полями, что поддерживает распространение волны, включающей эти поля, согласно Уравнения Максвелла. Электромагнитные волны могут проходить через вакуум и через некоторые диэлектрик среды (на длинах волн, на которых они считаются прозрачный). Электромагнитные волны в зависимости от их частот (или длины волн) имеют более конкретные обозначения, включая радиоволны, инфракрасная радиация, терагерцовые волны, видимый свет, ультрафиолетовая радиация, Рентгеновские лучи и гамма излучение.
Другие типы волн включают гравитационные волны, которые нарушают пространство-время которые распространяются согласно общая теория относительности; волны распространения тепла[сомнительный ]; плазменные волны сочетающие механические деформации и электромагнитные поля; реакционно-диффузионные волны, например, в Реакция Белоусова – Жаботинского; и многое другое.
Передача механических и электромагнитных волн энергия,[2], импульс, и Информация, но они не переносят частицы в среде. В математике и электроника волны изучаются как сигналы.[3] С другой стороны, некоторые волны конверты которые вообще не двигаются, такие как стоячие волны (которые имеют фундаментальное значение для музыки) и гидравлические прыжки. Некоторые, как волны вероятности из квантовая механика, может быть полностью статичным[сомнительный ].
Физическая волна почти всегда ограничена некоторой конечной областью пространства, называемой его домен. Например, сейсмические волны, генерируемые землетрясения имеют значение только внутри и на поверхности планеты, поэтому за ее пределами их можно игнорировать. Однако волны с бесконечной областью, которые распространяются по всему пространству, обычно изучаются в математике и являются очень ценными инструментами для понимания физических волн в конечных областях.
А плоская волна - важная математическая идеализация, в которой возмущение одинаково вдоль любой (бесконечной) плоскости нормальный к определенному направлению движения. Математически простейшая волна - это синусоидальный плоская волна, в которой в любой точке поле испытывает простые гармонические колебания на одной частоте. В линейных средах сложные волны обычно можно разложить как сумму многих синусоидальных плоских волн, имеющих разные направления распространения и / или разные частоты. Плоская волна классифицируется как поперечная волна если возмущение поля в каждой точке описывается вектором, перпендикулярным направлению распространения (также направлению передачи энергии); или же продольный если эти векторы точно в направление распространения. К механическим волнам относятся как поперечные, так и продольные волны; с другой стороны, плоские электромагнитные волны являются строго поперечными, в то время как звуковые волны в жидкостях (например, в воздухе) могут быть только продольными. Это физическое направление колеблющегося поля относительно направления распространения также называется волновым направлением. поляризация что может быть важным атрибутом для волн, имеющих более одной возможной поляризации.
Математическое описание
Одиночные волны
Волну можно описать так же, как поле, а именно как функция куда это позиция и время.
Значение это точка пространства, в частности, в области определения волны. С математической точки зрения это обычно вектор в Декартово трехмерное пространство . Однако во многих случаях можно игнорировать одно измерение и позволить быть точкой декартовой плоскости . Так обстоит дело, например, при изучении колебаний кожи барабана. Можно даже ограничить до точки декартовой прямой - то есть набор действительные числа. Так обстоит дело, например, при исследовании колебаний в струна для скрипки или же рекордер. Время , с другой стороны, всегда считается скаляр; то есть реальное число.
Значение может быть любая физическая величина интереса, присвоенная точке это может измениться со временем. Например, если представляет собой колебания внутри упругого твердого тела, величина обычно представляет собой вектор, который дает текущее смещение от материальных частиц, которые были бы в точке при отсутствии вибрации. Для электромагнитной волны значение может быть электрическое поле вектор , или магнитное поле вектор , или любое связанное количество, например Вектор Пойнтинга . В динамика жидкостей, значение может быть вектором скорости жидкости в точке , или любое скалярное свойство, например давление, температура, или же плотность. В химической реакции может быть концентрацией некоторого вещества в окрестности точки реакционной среды.
Для любого измерения (1, 2 или 3), тогда область волны будет подмножество из , такая, что значение функции определяется для любой точки в . Например, при описании движения кожа барабанаможно считать быть диск (круг) на плоскости с центром в начале координат , и разреши быть вертикальным смещением кожи в точке из и в свое время .
Волновые семьи
Иногда интересует конкретная волна. Однако чаще требуется понимать большой набор возможных волн; как и все способы, которыми кожа барабана может вибрировать после однократного удара барабанная палочка, или все возможные радар эхо можно было получить от самолет это может приближаться к аэропорт.
В некоторых из этих ситуаций такое семейство волн можно описать функцией это зависит от определенных параметры , Помимо и . Тогда можно получить разные волны, т. Е. Разные функции и - путем выбора различных значений для этих параметров.
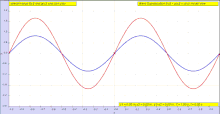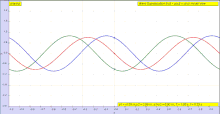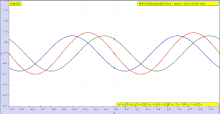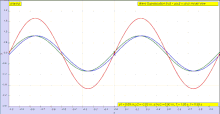
Например, звуковое давление внутри рекордер то, что играет "чистую" ноту, обычно стоячая волна, что можно записать как
Параметр определяет амплитуду волны (то есть максимальное звуковое давление в канале ствола, которое связано с громкостью ноты); скорость звука; - длина канала ствола; и положительное целое число (1,2,3, ...), определяющее количество узлы в стоячей волне. (Позиция следует измерять от мундштук, и время с любого момента, когда давление на мундштук максимально. Количество это длина волны эмитированной банкноты, и это его частота.) Многие общие свойства этих волн могут быть выведены из этого общего уравнения без выбора конкретных значений параметров.
В качестве другого примера может быть, что колебания обшивки барабана после одиночного удара зависят только от расстояния. от центра кожи до точки удара, а по силе забастовки. Тогда вибрацию для всех возможных ударов можно описать функцией .
Иногда интересующее семейство волн имеет бесконечно много параметров. Например, можно описать, что происходит с температурой металлического стержня, когда его сначала нагревают до различных температур в разных точках по длине, а затем дают ему остыть в вакууме. В этом случае вместо скаляра или вектора параметр должен быть функцией такой, что начальная температура в каждой точке бара. Тогда температуры в более поздние времена могут быть выражены функцией это зависит от функции (это функциональный оператор), так что температура в более позднее время
Дифференциальные волновые уравнения
Другой способ описать и изучить семейство волн - это дать математическое уравнение, которое вместо явного указания значения , только ограничивает то, как эти значения могут изменяться со временем. Тогда рассматриваемое семейство волн состоит из всех функций которые удовлетворяют этим ограничениям, то есть все решения уравнения.
Этот подход чрезвычайно важен в физике, потому что ограничения обычно являются следствием физических процессов, которые заставляют волну развиваться. Например, если температура внутри блока некоторых однородный и изотропный твердый материал, его эволюция сдерживается уравнение в частных производных
куда тепло, выделяемое на единицу объема и времени в окрестности вовремя (например, происходящими там химическими реакциями); - декартовы координаты точки ; является (первой) производной от относительно ; и - вторая производная от относительно . (Символ ""означает, что в производной по некоторой переменной все другие переменные должны считаться фиксированными.)
Это уравнение можно вывести из законов физики, регулирующих распространение тепла в твердых носителях. По этой причине его называют уравнение теплопроводности в математике, даже если это применимо ко многим другим физическим величинам, помимо температуры.
В качестве другого примера мы можем описать все возможные звуки, эхом отражающиеся в контейнере с газом, с помощью функции что дает давление в точке и время внутри этого контейнера. Если изначально газ имел одинаковую температуру и состав, эволюция ограничивается формулой
Здесь какая-то дополнительная сила сжатия, прикладываемая к газу около каким-то внешним процессом, таким как громкоговоритель или же поршень прямо рядом с .
Это же дифференциальное уравнение описывает поведение механических колебаний и электромагнитных полей в однородном изотропном непроводящем твердом теле. Обратите внимание, что это уравнение отличается от уравнения теплового потока только тем, что левая часть равна , вторая производная от по времени, а не по первой производной . Но это небольшое изменение имеет огромное значение для набора решений. . Это дифференциальное уравнение называется " волновое уравнение в математике, хотя он описывает только один очень особенный вид волн.
Волна в упругой среде
Рассмотрим путешествие поперечная волна (который может быть пульс) на веревочке (среде). Считайте, что струна имеет одно пространственное измерение. Считайте эту волну бегущей
- в направление в пространстве. Например, пусть положительный направление должно быть вправо, а отрицательное направление должно быть налево.
- с постоянным амплитуда
- с постоянной скоростью , куда является
- независим от длина волны (нет разброс)
- не зависит от амплитуды (линейный СМИ, а не нелинейный).[4][5]
- с постоянным форма волны, или форма
Тогда эту волну можно описать двумерными функциями
- (форма волны едет направо)
- (форма волны едет налево)
или, в более общем смысле, формула даламбера:[6]
представление двух компонентных сигналов и движутся через среду в противоположных направлениях. Обобщенное представление этой волны можно получить[7] как уравнение в частных производных
Общие решения основаны на Принцип Дюамеля.[8]
Формы волн
Форма или форма F в формула даламбера включает аргумент х - vt. Постоянные значения этого аргумента соответствуют постоянным значениям F, и эти постоянные значения возникают, если Икс увеличивается с той же скоростью, что и vt увеличивается. То есть волна в форме функции F будет двигаться в положительном Икс-направление по скорости v (и грамм будет распространяться с той же скоростью в отрицательном Икс-направление).[9]
В случае периодической функции F с периодом λ, то есть, F(х + λ − vt) = F(Икс − vt) периодичность F в пространстве означает, что снимок волны в данный момент т находит волну, периодически меняющуюся в пространстве с периодом λ (в длина волны волны). Подобным образом эта периодичность F подразумевает также периодичность во времени: F(Икс − v (t + T)) = F(Икс − vt) при условии vT = λ, поэтому наблюдение за волной в фиксированном месте Икс находит волну периодически волнообразную во времени с периодом Т = λ/v.[10]
Амплитуда и модуляция
Амплитуда волны может быть постоянной (в этом случае волна является c.w. или же непрерывная волна), или, может быть модулированный так, чтобы меняться со временем и / или положением. Контур изменения амплитуды называется конверт волны. Математически модулированная волна можно записать в виде:[11][12][13]
куда - огибающая амплитуды волны, это волновое число и это фаза. Если групповая скорость (см. ниже) не зависит от длины волны, это уравнение можно упростить как:[14]
показывая, что оболочка движется с групповой скоростью и сохраняет свою форму. В противном случае, в случаях, когда групповая скорость изменяется в зависимости от длины волны, форма импульса изменяется способом, который часто описывается с помощью уравнение конверта.[14][15]
Фазовая скорость и групповая скорость
Есть две скорости, которые связаны с волнами: фазовая скорость и групповая скорость.
Фазовая скорость - это скорость, с которой фаза волны распространяется в космосе: любая заданная фаза волны (например, гребень) будет двигаться с фазовой скоростью. Фазовая скорость выражается через длина волны λ (лямбда) и период Т в качестве
Групповая скорость - это свойство волн с определенной огибающей, измеряющее распространение в пространстве (то есть фазовую скорость) общей формы амплитуд волн - модуляции или огибающей волны.
Синусоидальные волны
Эта секция дубликаты объем других разделов, конкретно, Синусоидальная волна и Частота. (Июль 2015 г.) |

Математически самая основная волна - это (пространственно) одномерная волна. синусоидальная волна (также называемый гармоническая волна или же синусоида) с амплитудой описывается уравнением:
куда
- это максимум амплитуда волны - максимальное расстояние от наивысшей точки возмущения в среде (гребня) до точки равновесия за один волновой цикл. На рисунке справа это максимальное расстояние по вертикали между базовой линией и волной.
- это пространство координировать
- координата времени
- это волновое число
- это угловая частота
- это фазовая постоянная.
Единицы амплитуды зависят от типа волны. Поперечные механические волны (например, волна на струне) имеют амплитуду, выражаемую как расстояние (например, метры), продольные механические волны (например, звуковые волны) используют единицы давления (например, паскали), а электромагнитные волны (форма поперечной вакуумной волны) выражают амплитуду через ее электрическое поле (например, вольт / метр).
В длина волны это расстояние между двумя последовательными гребнями или впадинами (или другими эквивалентными точками), обычно измеряется в метрах. А волновое число , пространственная частота волны в радианы на единицу расстояния (обычно на метр), может быть связан с длиной волны соотношением
В период - время одного полного цикла колебания волны. В частота количество периодов в единицу времени (в секунду), обычно измеряется в герц обозначается как Гц. Они связаны:
Другими словами, частота и период волны взаимны.
В угловая частота представляет частоту в радианах в секунду. Это связано с частотой или периодом
Длина волны синусоидального сигнала, движущегося с постоянной скоростью дан кем-то:[16]
куда называется фазовой скоростью (величина фазовая скорость) волны и - частота волны.
Длина волны может быть полезным понятием, даже если волна не периодический в космосе. Например, когда океанская волна приближается к берегу, набегающая волна волнообразно колеблется. местный длина волны, которая частично зависит от глубины морского дна по сравнению с высотой волны. Анализ волны может быть основан на сравнении локальной длины волны с местной глубиной воды.[17]
Хотя волны произвольной формы будут распространяться без потерь без потерь линейные инвариантные во времени системы, при наличии дисперсии синусоидальная волна - это уникальная форма, которая будет распространяться без изменений, но по фазе и амплитуде, что упрощает анализ.[18] Из-за Отношения Крамерса – Кронигалинейная среда с дисперсией также имеет потери, поэтому синусоидальная волна, распространяющаяся в дисперсионной среде, ослабляется в определенных частотных диапазонах, которые зависят от среды.[19]В функция синуса является периодическим, поэтому синусоидальная волна или синусоида имеет длина волны в пространстве и период времени.[20][21]
Синусоида определена для всех времен и расстояний, тогда как в физических ситуациях мы обычно имеем дело с волнами, которые существуют в течение ограниченного промежутка времени и продолжительности во времени. Произвольную форму волны можно разложить на бесконечный набор синусоидальных волн с помощью Анализ Фурье. В результате простой случай одиночной синусоидальной волны может быть применен к более общим случаям.[22][23] В частности, многие СМИ линейный, или почти так, поэтому расчет поведения произвольной волны можно найти путем сложения откликов на отдельные синусоидальные волны с помощью принцип суперпозиции найти решение для общей формы волны.[24] Когда среда нелинейный, то ответ на сложные волны не может быть определен с помощью синусоидального разложения.
Плоские волны
А плоская волна это своего рода волна, величина которой изменяется только в одном пространственном направлении. То есть его значение постоянно на плоскости, перпендикулярной этому направлению. Плоские волны можно задать вектором единичной длины указывает направление, в котором изменяется волна, и профиль волны, описывающий, как волна изменяется в зависимости от смещения вдоль этого направления () и время (). Поскольку профиль волны зависит только от положения в сочетании , любое смещение в направлениях, перпендикулярных не может повлиять на значение поля.
Плоские волны часто используются для моделирования электромагнитные волны далеко от источника. Для плоских электромагнитных волн электрическое и магнитное поля сами по себе поперечны по отношению к направлению распространения, а также перпендикулярны друг другу.
Стоячие волны

Стоячая волна, также известная как стационарная волна, - волна, конверт остается в постоянном положении. Это явление возникает в результате вмешательство между двумя волнами, движущимися в противоположных направлениях.
В сумма двух встречных волн (одинаковой амплитуды и частоты) создает стоячая волна. Стоячие волны обычно возникают, когда граница блокирует дальнейшее распространение волны, тем самым вызывая отражение волны и, следовательно, вводя встречную волну. Например, когда скрипка струна смещается, поперечные волны распространяются туда, где струна удерживается на месте в мост и орех, где волны отражаются обратно. У бриджа и гайки две противоположные волны находятся в противофаза и отменяют друг друга, производя узел. На полпути между двумя узлами есть пучность, где две встречные волны усиливать друг друга максимально. Нет сети распространение энергии через некоторое время.
Одномерные стоячие волны; то фундаментальный режим и первые 5 обертоны.
Двумерный стоячая волна на диске; это основной режим.
А стоячая волна на диске с пересечением двух узловых линий в центре; это обертон.
Физические свойства
Волны демонстрируют обычное поведение в ряде стандартных ситуаций, например:
Передача и СМИ
Волны обычно движутся по прямой (т. Е. Прямолинейно) через среда передачи. Такие носители можно разделить на одну или несколько из следующих категорий:
- А ограниченная среда если он конечен по протяженности, в противном случае неограниченная среда
- А линейная среда если можно сложить амплитуды различных волн в любой конкретной точке среды
- А однородная среда или же однородная среда если его физические свойства не изменяются в разных точках космоса
- An анизотропная среда если одно или несколько его физических свойств отличаются в одном или нескольких направлениях
- An изотропная среда если его физические свойства одно и тоже во всех направлениях
Абсорбция
Волны обычно определяются в средах, которые позволяют большей или всей энергии волны распространяться без потеря. Однако материалы можно охарактеризовать как «с потерями», если они отбирают энергию из волны, обычно превращая ее в тепло. Это называется «поглощением». Материал, который поглощает энергию волны при пропускании или отражении, характеризуется показатель преломления который сложный. Величина поглощения обычно зависит от частоты (длины волны) волны, которая, например, объясняет, почему объекты могут казаться окрашенными.
Отражение
Когда волна ударяется об отражающую поверхность, она меняет направление, так что угол, образованный падающая волна и линия нормальный к поверхности равен углу между отраженной волной и той же нормальной линией.
Преломление
Преломление - это явление, когда волна меняет свою скорость. Математически это означает, что размер фазовая скорость изменения. Обычно рефракция возникает, когда волна проходит от одного средний в другой. Величина, на которую волна преломляется материалом, определяется показатель преломления материала. Направления падения и преломления связаны с показателями преломления двух материалов соотношением Закон Снеллиуса.
Дифракция
Волна демонстрирует дифракцию, когда сталкивается с препятствием, которое изгибает волну, или когда она распространяется после выхода из отверстия. Эффекты дифракции более выражены, когда размер препятствия или отверстия сопоставим с длиной волны.
Вмешательство

Когда волны в линейной среде (обычный случай) пересекают друг друга в какой-то области пространства, они фактически не взаимодействуют друг с другом, а продолжают существовать, как если бы другая не присутствовала. Однако в любой момент в этот регион полевые количества описывая эти волны, добавляют в соответствии с принцип суперпозиции. Если волны имеют одинаковую частоту в фиксированном фаза отношения, то обычно будут позиции, в которых две волны в фазе и их амплитуды Добавить, и другие должности, где они не в фазе и их амплитуды (частично или полностью) Отмена. Это называется картина интерференции.
Поляризация
Явление поляризации возникает, когда волновое движение может происходить одновременно в двух ортогональный направления. Поперечные волны могут быть поляризованы, например. Когда поляризация используется в качестве дескриптора без оговорок, это обычно относится к частному, простому случаю линейная поляризация. Поперечная волна является линейно поляризованной, если она колеблется только в одном направлении или плоскости. В случае линейной поляризации часто бывает полезно добавить относительную ориентацию этой плоскости, перпендикулярную направлению движения, в котором происходят колебания, например, «горизонтальная», если плоскость поляризации параллельна направлению движения. земля. Электромагнитные волны распространяющиеся в свободном пространстве, например, являются поперечными; они могут быть поляризованы с помощью поляризационный фильтр.
Продольные волны, такие как звуковые волны, не обладают поляризацией. Для этих волн существует только одно направление колебаний, то есть вдоль направления движения.
Дисперсия
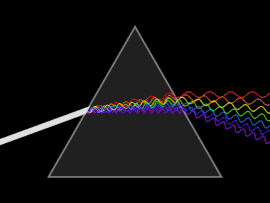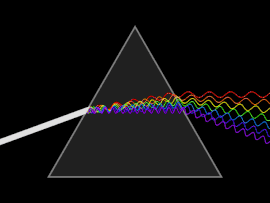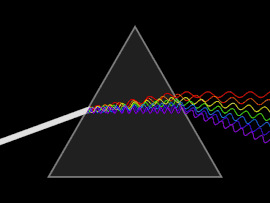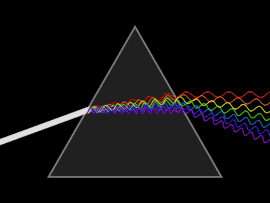
Волна рассеивается, когда либо фазовая скорость или групповая скорость зависит от частоты волны. Дисперсию легче всего увидеть, если пропустить белый свет через призма, в результате чего получается спектр цветов радуги. Исаак Ньютон провел эксперименты со светом и призмами, представив свои выводы в Opticks (1704), что белый свет состоит из нескольких цветов и что эти цвета больше не могут быть разложены.[25]
Механические волны
Волны на струнах
Скорость поперечной волны, бегущей по вибрирующая струна ( v ) прямо пропорционален квадратному корню из напряжение строки ( Т ) над линейная массовая плотность ( μ ):
где линейная плотность μ - масса на единицу длины струны.
Акустические волны
Акустический или звук волны распространяются со скоростью, заданной
или квадратный корень из адиабатического модуля объемной упругости, деленный на плотность окружающей среды (см. скорость звука).
Волны на воде
- Рябь на поверхности водоема на самом деле находится сочетание поперечных и продольных волн; следовательно, точки на поверхности следуют орбитальным путям.
- Звук - механическая волна, распространяющаяся через газы, жидкости, твердые тела и плазму;
- Инерционные волны, которые возникают во вращающихся жидкостях и восстанавливаются Эффект Кориолиса;
- Волны на поверхности океана, которые представляют собой возмущения, распространяющиеся через воду.
Сейсмические волны
Сейсмические волны - это волны энергии, которые проходят через слои Земли и являются результатом землетрясений, извержений вулканов, движения магмы, крупных оползней и крупных искусственных взрывов, которые излучают низкочастотную акустическую энергию.
Эффект Допплера
В Эффект Допплера (или Доплеровский сдвиг) - изменение частота из волна в отношении наблюдатель кто движется относительно источника волны.[26] Он назван в честь Австрийский физик Кристиан Доплер, описавший явление в 1842 году.
Ударные волны
Ударная волна - это тип распространяющегося возмущения. Когда волна движется быстрее местной скорость звука в жидкость, это ударная волна. Подобно обыкновенной волне, ударная волна несет энергию и может распространяться через среду; однако для него характерно резкое, почти прерывистое изменение давление, температура и плотность среды.[27]
Другой
- Волны трафик, то есть распространение транспортных средств различной плотности и т. д., которые можно моделировать как кинематические волны[28]
- Метахрональная волна относится к появлению бегущей волны, вызванной согласованными последовательными действиями.
Электромагнитные волны
Электромагнитная волна состоит из двух волн, которые являются колебаниями электрический и магнитный поля. Электромагнитная волна распространяется в направлении, перпендикулярном направлению колебаний обоих полей. В 19 веке, Джеймс Клерк Максвелл показал, что в вакуумэлектрическое и магнитное поля удовлетворяют условию волновое уравнение оба со скоростью, равной скорости скорость света. Отсюда возникла идея, что свет электромагнитная волна. Электромагнитные волны могут иметь разные частоты (и, следовательно, длины волн), вызывая различные типы излучения, такие как радиоволны, микроволны, инфракрасный, видимый свет, ультрафиолетовый, Рентгеновские лучи, и Гамма излучение.
Квантово-механические волны
Уравнение Шредингера
В Уравнение Шредингера описывает волнообразное поведение частиц в квантовая механика. Решениями этого уравнения являются волновые функции которое можно использовать для описания плотности вероятности частицы.
Уравнение Дирака
В Уравнение Дирака представляет собой релятивистское волновое уравнение, детализирующее электромагнитные взаимодействия. Волны Дирака совершенно строго объясняют мелкие детали спектра водорода. Волновое уравнение также подразумевало существование новой формы материи, антивещества, о которой раньше не подозревали и не наблюдали, и что было подтверждено экспериментально. В контексте квантовой теории поля уравнение Дирака переосмысливается для описания квантовых полей, соответствующих частицам со спином 1/2.

волны де Бройля
Луи де Бройль постулировал, что все частицы с импульс иметь длину волны
куда час является Постоянная Планка, и п это величина импульс частицы. Эта гипотеза легла в основу квантовая механика. В настоящее время эту длину волны называют длина волны де Бройля. Например, электроны в ЭЛТ дисплей имеют длину волны де Бройля около 10−13 м.
Волна, представляющая такую частицу, движущуюся в k-направление выражается волновой функцией следующим образом:
где длина волны определяется волновой вектор k в качестве:
и импульс:
Однако такая волна с определенной длиной волны не локализована в пространстве и поэтому не может представлять собой частицу, локализованную в пространстве. Чтобы локализовать частицу, де Бройль предложил суперпозицию разных длин волн в диапазоне от центрального значения в волновой пакет,[30] форма волны, часто используемая в квантовая механика описать волновая функция частицы. В волновом пакете длина волны частицы не точна, и локальная длина волны отклоняется в обе стороны от значения основной длины волны.
Представляя волновую функцию локализованной частицы, волновой пакет часто считается Гауссова форма и называется Гауссов волновой пакет.[31] Гауссовские волновые пакеты также используются для анализа волн на воде.[32]
Например, гауссова волновая функция ψ может иметь вид:[33]
в какое-то начальное время т = 0, где центральная длина волны связана с центральным волновым вектором k0 поскольку λ0 = 2π / k0. Это хорошо известно из теории Анализ Фурье,[34] или из Принцип неопределенности Гейзенберга (в случае квантовой механики), что для создания локализованного волнового пакета необходим узкий диапазон длин волн, и чем более локализована огибающая, тем больше разброс требуемых длин волн. В преобразование Фурье гауссиана сама по себе является гауссовой[35] Учитывая гауссовский:
преобразование Фурье:
Следовательно, гауссиан в пространстве состоит из волн:
то есть, количество волн с длинами волн λ таких, что kλ = 2 π.
Параметр σ определяет пространственный разброс гауссиана вдоль Икс-оси, а преобразование Фурье показывает разброс волновой вектор k определяется 1 / σ. То есть, чем меньше размер в пространстве, тем больше размер в пространстве. k, а значит, в λ = 2πk.

Гравитационные волны
Гравитационные волны волны, генерируемые в текучей среде или на границе раздела двух сред, когда сила тяжести или плавучесть пытается восстановить равновесие. Один из примеров - рябь на пруду.
Гравитационные волны
Гравитационные волны также путешествуют по космосу. О первом наблюдении гравитационных волн было объявлено 11 февраля 2016 года.[36]Гравитационные волны - это нарушения кривизны пространство-время, предсказанный теорией Эйнштейна общая теория относительности.
Смотрите также
Волны в целом
- Волновое уравнение, Общее
- Распространение волн, любой из способов распространения волн
- Помехи (распространение волн), явление, при котором две волны накладываются друг на друга, образуя результирующую волну
- Механическая волнав СМИ
- Волновое движение (журнал), научный журнал
- Волновой фронт, наступающая поверхность распространения волны
Параметры
- Фаза (волны), смещение или угол синусоидальной волновой функции в ее начале
- Коэффициент стоячей волны, в телекоммуникациях
- Длина волны
- Волновое число
- Период волны
Формы волны
- Ползучая волна, волна, дифрагированная вокруг сферы
- Неувядающая волна
- Продольная волна
- Периодическая бегущая волна
- Синусоидальная волна
- Квадратная волна
- Стоячая волна
- Поперечная волна
Электромагнитные волны
- Дьяконовские поверхностные волны
- Волна Дьяконова-Фойгта
- Волновод Земля-Ионосфера, в радиопередаче
- Электромагнитная волна
- Уравнение электромагнитной волны, описывает распространение электромагнитной волны
- СВЧ, форма электромагнитного излучения
В жидкостях
- Теория волн Эйри, в гидродинамике
- Капиллярная волна, в гидродинамике
- Кноидальная волна, в гидродинамике
- Краевая волна, поверхностная гравитационная волна, рефракционно закрепленная на жесткой границе
- Волна Фарадея, тип волны в жидкостях
- Гравитационная волна, в гидродинамике
- Звуковая волна, волна звук через среду, такую как воздух или вода
- Ударная волна, в аэродинамике
- Внутренняя волна, волна в жидкой среде
- Приливная волна, научно неверное название для цунами
- Волна Толлмина – Шлихтинга, в гидродинамике
В квантовой механике
В теории относительности
- Гравитационная волна, в теории относительности
- Релятивистские волновые уравнения, волновые уравнения, учитывающие специальную теорию относительности
- pp-волна пространство-время, набор точных решений полевого уравнения Эйнштейна
Другие специфические типы волн
- Альфвеновская волна, в науке о частицах
- Атмосферная волна, периодическое возмущение в полях атмосферных переменных
- Пихтовая волна, конфигурация леса
- Волны ягненка, в твердых материалах
- Волны Рэлея, поверхностные акустические волны, распространяющиеся по твердым телам.
- Спиновая волна, в магнетизме
- Волна спиновой плотности, в твердых материалах
- Троянский волновой пакет, в науке о частицах
- Волны в плазме, в науке о частицах
похожие темы
- Beat (акустика)
- Киматика
- Эффект Допплера
- Детектор конверта
- Групповая скорость
- Гармонический
- Указатель волновых статей
- Инерционная волна
- Список волн, названных в честь людей
- Фазовая скорость
- Система реакция – диффузия
- Резонанс
- Пульсационный бак
- Разбойная волна
- Уравнения мелкой воды
- Волновая машина Shive
- Звук
- Стоячая волна
- Среда передачи
- Волновая турбулентность
- Ветровая волна
Рекомендации
- ^ Сантос, Эдгар; Шёлль, Михаэль; Санчес-Поррас, Ренан; Dahlem, Markus A .; Силосы, Умберто; Унтерберг, Андреас; Дикхаус, Хартмут; Саковиц, Оливер В. (2014-10-01). «В гринцефалическом мозге возникают радиальные, спиральные и отражающие волны распространяющейся деполяризации». NeuroImage. 99: 244–255. Дои:10.1016 / j.neuroimage.2014.05.021. ISSN 1095-9572. PMID 24852458. S2CID 1347927.
- ^ (Холл 1982, п. 8)
- ^ Прагнан Чакраворти, «Что такое сигнал? [Конспекты лекции]», IEEE Журнал обработки сигналов, т. 35, нет. 5, стр. 175-177, сентябрь 2018 г.Дои:10.1109 / MSP.2018.2832195
- ^ Майкл А. Славинский (2003). «Волновые уравнения». Сейсмические волны и лучи в упругих средах. Эльзевир. стр.131 ff. ISBN 978-0-08-043930-3.
- ^ Лев А. Островский и Александр И. Потапов (2001). Модулированные волны: теория и применение. Издательство Университета Джона Хопкинса. ISBN 978-0-8018-7325-6.
- ^ Карл Ф. Грааф (1991). Волновое движение в упругих телах (Перепечатка Оксфордского изд. 1975 г.). Дувр. С. 13–14. ISBN 978-0-486-66745-4.
- ^ Для примера вывода см. Шаги, ведущие к ур. (17) в Фрэнсис Редферн. «Кинематический вывод волнового уравнения». Физический журнал.
- ^ Джалал М. Ихсан Шатах; Майкл Струве (2000). «Линейное волновое уравнение». Геометрические волновые уравнения. Книжный магазин Американского математического общества. стр.37ff. ISBN 978-0-8218-2749-9.
- ^ Луи Лайонс (1998). Все, что вы хотели знать о математике, но боялись спросить. Издательство Кембриджского университета. стр.128 ff. ISBN 978-0-521-43601-4.
- ^ Александр Макферсон (2009). «Волны и их свойства». Введение в кристаллографию макромолекул (2-е изд.). Вайли. п. 77. ISBN 978-0-470-18590-2.
- ^ Кристиан Джираушек (2005). Лазерная динамика с FEW-циклом и определение фазы огибающей носителя. Cuvillier Verlag. п. 9. ISBN 978-3-86537-419-6.
- ^ Фриц Курт Кнойбюль (1997). Колебания и волны. Springer. п. 365. ISBN 978-3-540-62001-3.
- ^ Марк Лундстрем (2000). Основы перевозки грузов. Издательство Кембриджского университета. п. 33. ISBN 978-0-521-63134-1.
- ^ а б Чин-Лин Чен (2006). «§13.7.3 Огибающая импульса в недисперсных средах». Основы волноводной оптики. Вайли. п. 363. ISBN 978-0-471-75687-3.
- ^ Стефано Лонги; Давиде Яннер (2008). «Локализация и волновые пакеты Ванье в фотонных кристаллах». В Уго Э. Эрнандес-Фигероа; Мишель Замбони-Ракед; Эразмо Реками (ред.). Локализованные волны. Wiley-Interscience. п. 329. ISBN 978-0-470-10885-7.
- ^ Дэвид К. Кэссиди; Джеральд Джеймс Холтон; Флойд Джеймс Резерфорд (2002). Понимание физики. Birkhäuser. стр.339ff. ISBN 978-0-387-98756-9.
- ^ Пол Р. Пинет (2009). op. cit. п. 242. ISBN 978-0-7637-5993-3.
- ^ Миша Шварц; Уильям Р. Беннет и Сеймур Штайн (1995). Коммуникационные системы и методы. Джон Уайли и сыновья. п. 208. ISBN 978-0-7803-4715-1.
- ^ См. Уравнение. 5.10 и обсуждение в A.G.G.M. Тиленс (2005). Физика и химия межзвездной среды. Издательство Кембриджского университета. стр.119 ff. ISBN 978-0-521-82634-1.; Уравнение 6.36 и связанное обсуждение в Отфрид Маделунг (1996). Введение в теорию твердого тела (3-е изд.). Springer. стр.261 ff. ISBN 978-3-540-60443-3.; и уравнение. 3,5 дюйма Ф Майнарди (1996). «Переходные волны в линейных вязкоупругих средах». В Ардешире Гуране; А. Бостром; Герберт Убералл; О. Лерой (ред.). Акустические взаимодействия с подводными упругими конструкциями: неразрушающий контроль, распространение и рассеяние акустических волн. World Scientific. п. 134. ISBN 978-981-02-4271-8.
- ^ Александр Тихонович Филиппов (2000). Универсальный солитон. Springer. п. 106. ISBN 978-0-8176-3635-7.
- ^ Сет Штайн, Майкл Э. Визессион (2003). Введение в сейсмологию, землетрясения и структуру земли. Вили-Блэквелл. п. 31. ISBN 978-0-86542-078-6.
- ^ Сет Штайн, Майкл Э. Визессион (2003). op. соч.. п. 32. ISBN 978-0-86542-078-6.
- ^ Кимбалл А. Милтон; Джулиан Сеймур Швингер (2006). Электромагнитное излучение: вариационные методы, волноводы и ускорители. Springer. п. 16. ISBN 978-3-540-29304-0.
Таким образом, произвольная функция ж(р, т) могут быть синтезированы правильной суперпозицией функций exp[я (k · r−ωт)]...
- ^ Раймонд А. Сервей и Джон В. Джуэтт (2005). «§14.1 Принцип суперпозиции». Принципы физики (4-е изд.). Cengage Learning. п. 433. ISBN 978-0-534-49143-7.
- ^ Ньютон, Исаак (1704). "Prop VII Theor V". Opticks: Или, трактат об отражениях, преломлениях, изгибах и цветах света. Также два трактата о видах и величине криволинейных фигур.. 1. Лондон. п. 118.
Все Цвета во Вселенной, созданные Светом ... являются Цветами однородных Светов или составлены из них ...
- ^ Джордано, Николас (2009). Физика в колледже: рассуждения и отношения. Cengage Learning. С. 421–424. ISBN 978-0534424718.
- ^ Андерсон, Джон Д. мл. (Январь 2001 г.) [1984], Основы аэродинамики (3-е изд.), МакГроу-Хилл Наука / Инженерия / Математика, ISBN 978-0-07-237335-6
- ^ М.Дж. Лайтхилл; Г. Б. Whitham (1955). «О кинематических волнах. II. Теория транспортного потока на длинных людных дорогах». Труды Лондонского королевского общества. Серия А. 229 (1178): 281–345. Bibcode:1955RSPSA.229..281L. CiteSeerX 10.1.1.205.4573. Дои:10.1098 / RSPA.1955.0088. S2CID 18301080.CS1 maint: ref = harv (связь) И: ЧИСЛО ПИ. Ричардс (1956). «Удары по трассе». Исследование операций. 4 (1): 42–51. Дои:10.1287 / opre.4.1.42.CS1 maint: ref = harv (связь)
- ^ В. Фромхолд (1991). «Волновые пакетные решения». Квантовая механика в прикладной физике и технике (Перепечатка Academic Press, 1981 изд.). Courier Dover Publications. стр.59 ff. ISBN 978-0-486-66741-6.
(стр.61) ... отдельные волны движутся медленнее, чем пакет, и поэтому проходят обратно через пакет по мере его продвижения
- ^ Мин Чан Ли (1980). «Электронная интерференция». У Л. Мартона; Клэр Мартон (ред.). Успехи электроники и электронной физики. 53. Академическая пресса. п. 271. ISBN 978-0-12-014653-6.
- ^ См. Например Уолтер Грайнер; Д. Аллан Бромли (2007). Квантовая механика (2-е изд.). Springer. п. 60. ISBN 978-3-540-67458-0. и Джон Джозеф Гилман (2003). Электронная основа прочности материалов. Издательство Кембриджского университета. п. 57. ISBN 978-0-521-62005-5.,Дональд Д. Фиттс (1999). Принципы квантовой механики. Издательство Кембриджского университета. п. 17. ISBN 978-0-521-65841-6..
- ^ Чанг К. Мэй (1989). Прикладная динамика поверхностных волн океана (2-е изд.). World Scientific. п. 47. ISBN 978-9971-5-0789-3.
- ^ Уолтер Грайнер; Д. Аллан Бромли (2007). Квантовая механика (2-е изд.). Springer. п. 60. ISBN 978-3-540-67458-0.
- ^ Зигмунд Брандт; Ханс Дитер Дамен (2001). Книжка с картинками по квантовой механике (3-е изд.). Springer. п. 23. ISBN 978-0-387-95141-6.
- ^ Сайрус Д. Кантрелл (2000). Современные математические методы для физиков и инженеров. Издательство Кембриджского университета. п.677. ISBN 978-0-521-59827-9.
- ^ «Гравитационные волны обнаружены впервые», открывает новое окно во Вселенной.'". CBC. 11 февраля 2016.
Источники
- Fleisch, D .; Киннаман, Л. (2015). Справочник по волнам для студентов. Кембридж: Издательство Кембриджского университета. Bibcode:2015sgw..book ..... F. ISBN 978-1107643260.CS1 maint: ref = harv (связь)
- Кэмпбелл, Мюррей; Greated, Клайв (2001). Путеводитель музыканта по акустике (Ред. Ред.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0198165057.
- Френч, A.P. (1971). Колебания и волны (серия Введение в физику M.I.T.). Нельсон Торнс. ISBN 978-0-393-09936-2. OCLC 163810889.
- Холл, Д. (1980). Музыкальная акустика: введение. Белмонт, Калифорния: Издательская компания Wadsworth. ISBN 978-0-534-00758-4.CS1 maint: ref = harv (связь).
- Хант, Фредерик Винтон (1978). Истоки в акустике. Вудбери, штат Нью-Йорк: Издано Американским акустическим обществом через Американский институт физики. ISBN 978-0300022209.
- Островский, Л.А .; Потапов, А. (1999). Модулированные волны, теория и приложения. Балтимор: Издательство Университета Джона Хопкинса. ISBN 978-0-8018-5870-3.CS1 maint: ref = harv (связь).
- Griffiths, G .; Schiesser, W.E. (2010). Анализ бегущей волны уравнений с частными производными: численные и аналитические методы с помощью Matlab и Maple. Академическая пресса. ISBN 9780123846532.