WikiDer > Категория отношений
В математика, то категория Rel имеет класс наборы так как объекты и бинарные отношения так как морфизмы.
Морфизм (или стрелка) р : А → B в этой категории есть отношение между множествами А и B, так р ⊆ А × B.
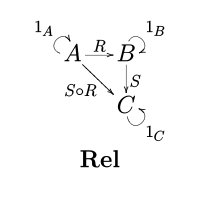
В композиция двух отношений р: А → B и S: B → C дан кем-то
- (а, c) ∈ S о р ⇔ для некоторых б ∈ B, (а, б) ∈ р и (б, c) ∈ S.[1]
Rel также была названа «категорией соответствий множеств».[2]
Свойства
Категория Rel имеет категория наборов Набор как (широкий) подкатегория, где стрелка ж : Икс → Y в Набор соответствует соотношению F ⊆ Икс × Y определяется (Икс, у) ∈ F ⇔ ж(Икс) = у.[3][4]
Морфизм в Rel является отношением, а соответствующий морфизм в противоположная категория к Rel стрелки перевернуты, так что это обратное отношение. Таким образом Rel содержит свою противоположность и является самодвойственный.[5]
В инволюция представленное обратным соотношением, дает кинжал делать Rel а категория кинжала.
В категории два функторы в себя, данный хом функтор: А бинарное отношение р ⊆ А × B и его транспонировать рТ ⊆ B × А может быть составлен как R RТ или как рТ р. Первая композиция дает однородное отношение на А а второй включен B. Поскольку образы этих гом-функторов лежат в Rel сам, в этом случае hom является внутренний функтор hom. Со своим внутренним функтором hom, Rel это закрытая категория, а также кинжал компактная категория.
Категория Rel можно получить из категории Набор как Категория Клейсли для монада чей функтор соответствует набор мощности, интерпретируемый как ковариантный функтор.
Возможно, на первый взгляд немного удивителен тот факт, что товар в Rel дается несвязный союз[5]:181 (а не декартово произведение как это в Набор), как и сопродукт.
Rel является моноидально закрытый, с моноидальным произведением А ⊗ B и внутренний дом А ⇒ B данный декартово произведение наборов.
Категория Rel был прототипом алгебраической структуры, названной аллегория от Питер Дж. Фрейд и Андре Щедров в 1990 году.[6] Начиная с обычная категория и функтор F: А → Bотмечают свойства индуцированного функтора Rel (А, Б) → Отн (FA, FB). Например, он сохраняет композицию, преобразование и пересечение. Такие свойства затем используются для создания аксиом для аллегории.
Отношения как объекты
Дэвид Райдхард и Род Берстолл рассматривать Rel иметь объекты, являющиеся однородными отношениями. Например, А это набор и р ⊆ А × А является бинарным отношением на А. Морфизмы этой категории - это функции между множествами, сохраняющие отношение: скажем, S ⊆ B × B это второе отношение и ж: А → B функция такая, что тогда ж это морфизм.[7]
Эту же идею выдвигают Адамек, Херрлих и Штрекер, где они обозначают объекты (А, Р) и (B, S), множество и отношение.[8]
использованная литература
- ^ Мак Лейн, С. (1988). Категории для рабочего математика (1-е изд.). Нью-Йорк: Springer-Verlag. п. 26. ISBN 0-387-90035-7.
- ^ Парейгис, Бодо (1970). Категории и функторы. Чистая и прикладная математика. 39. Академическая пресса. п. 6. ISBN 978-0-12-545150-5.
- ^ Эта категория называется НаборRel Райдхарда и Берстолла.
- ^ Джордж Бергман (1998), Приглашение к общей алгебре и универсальным конструкциям, §7.2 RelSet, Издательство Генри Хельсона, Беркли. ISBN 0-9655211-4-1.
- ^ а б Майкл Барр & Чарльз Уэллс (1998) Категория Теория для компьютерных ученых В архиве 2016-03-04 в Wayback Machine, стр. 83, из Университет Макгилла
- ^ Питер Дж. Фрейд И Андре Щедров (1990) Категории, Аллегории, страницы 79, 196, Северная Голландия ISBN 0-444-70368-3
- ^ Дэвид Райдхард и Род Берстолл (1988) Теория вычислительных категорий, стр. 54, Prentice-Hall ISBN 978-0131627369
- ^ Юрий Адамек, Хорст Херрлих и Джордж Э. Стрекер (2004) [1990] Абстрактные и конкретные категории, раздел 3.3, пример 2 (d) стр. 22, из Исследовательская группа КатМАТ в Бременский университет
- Фрэнсис Борсо (1994). Справочник категориальной алгебры: Том 2, Категории и структуры. Издательство Кембриджского университета. п. 115. ISBN 978-0-521-44179-7.