WikiDer > Фильтр Чебышева
| Линейный аналог электронные фильтры |
|---|
|
Простые фильтры |
Введение в эту статью может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов. (Ноябрь 2019) (Узнайте, как и когда удалить этот шаблон сообщения) |
Фильтры Чебышева находятся аналог или же цифровой фильтры, имеющие более крутой скатывание чем Фильтры Баттерворта, и имеют полоса пропускания рябь (тип I) или полоса задерживания рябь (тип II). Фильтры Чебышева обладают тем свойством, что они минимизируют ошибку между идеализированной и фактической характеристиками фильтра в диапазоне фильтра (см. Ссылки, например, [Daniels], [Lutovac]),[нужна цитата] но с рябью в полосе пропускания. Этот тип фильтра назван в честь Пафнутый Чебышев потому что его математические характеристики получены из Полиномы ЧебышеваФильтры Чебышева I типа обычно называют просто «фильтрами Чебышева», а фильтры II типа - «обратными фильтрами Чебышева».
Из-за пульсации полосы пропускания, присущей фильтрам Чебышева, для некоторых приложений предпочтительны те, которые имеют более плавный отклик в полосе пропускания, но более нерегулярный отклик в полосе задерживания.[нужна цитата]
Фильтры Чебышева типа I (фильтры Чебышева)
Фильтры Чебышева первого типа являются наиболее распространенными типами фильтров Чебышева. Прирост (или амплитуда) отклик, , как функция угловой частоты из пфильтр нижних частот -го порядка равен абсолютному значению передаточной функции оценивается в :
куда коэффициент пульсации, это частота среза и это Полином Чебышева из -й заказ.
Полоса пропускания демонстрирует равноволновое поведение, при этом пульсация определяется коэффициентом пульсации. . В полосе пропускания полином Чебышева чередуется между -1 и 1, поэтому усиление фильтра чередуется между максимумами на грамм = 1 и минимумов при .
Таким образом, коэффициент пульсации ε связан с пульсацией полосы пропускания δ в децибелы к:
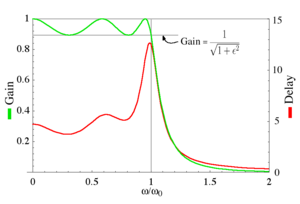
На частоте среза усиление снова имеет значение но продолжает падать в полоса задерживания по мере увеличения частоты. Это поведение показано на диаграмме справа. Обычная практика определения частоты среза на −3 дБ обычно не применяется к фильтрам Чебышева; вместо этого отсечка принимается как точка, в которой усиление падает до значения пульсации в последний раз.
Частота 3 дБ ωЧАС относится к ω0 к:
Порядок фильтра Чебышева равен количеству реактивный компоненты (например, индукторы), необходимого для реализации фильтра с использованием аналоговая электроника.
Еще круче скатывание можно получить, если в полосе задерживания разрешена пульсация, разрешив нули на -ось в комплексной плоскости. Однако это приводит к меньшему подавлению в полосе задерживания. Результат называется эллиптический фильтр, также известный как фильтр Кауэра.
Полюсы и нули

Для простоты предполагается, что частота среза равна единице. Полюса функции усиления фильтра Чебышева - нули знаменателя функции усиления. Использование комплексной частоты s, это происходит, когда:
Определение и, используя тригонометрическое определение полиномов Чебышева, получаем:
Решение для
где несколько значений функции арккосинуса сделаны явными с использованием целочисленного индекса м. Полюсы функции усиления Чебышева тогда:
Используя свойства тригонометрических и гиперболических функций, это можно записать в явно сложной форме:
куда м = 1, 2,..., п и
Это можно рассматривать как параметрическое уравнение в и это показывает, что полюса лежат на эллипсе в s-Космос сосредоточен на s = 0 с действительной полуосью длины и воображаемой полуоси длиной
Передаточная функция
Вышеприведенное выражение дает полюса усиления грамм. Для каждого комплексного полюса есть еще один, который является комплексно сопряженным, и для каждой сопряженной пары есть еще два, которые являются отрицательными для пары. В функция передачи должен быть стабильным, чтобы его полюса были полюсами усиления, которые имеют отрицательные действительные части и, следовательно, лежат в левой полуплоскости комплексного частотного пространства. Тогда передаточная функция определяется выражением
куда - это только те полюса усиления с отрицательным знаком перед действительным членом в приведенном выше уравнении для полюсов.
Групповая задержка
В групповая задержка определяется как производная фазы по угловой частоте и является мерой искажения сигнала, вносимого разностью фаз для разных частот.
Коэффициент усиления и групповая задержка для фильтра Чебышева пятого порядка типа I с ε = 0,5 показаны на графике слева. Можно видеть, что есть колебания в усилении и групповой задержке в полосе пропускания, но не в полосе задерживания.
Фильтры Чебышева II типа (обратные фильтры Чебышева)
Также известный как обратные фильтры Чебышева, тип фильтра Чебышева II типа встречается реже, потому что он не спадает так быстро, как тип I, и требует большего количества компонентов. У него нет пульсации в полосе пропускания, но есть равномерный в полосе задерживания. Прирост составляет:
В полосе задерживания полином Чебышева колеблется между -1 и 1, так что коэффициент усиления будет колебаться между нулем и
а наименьшая частота, при которой достигается этот максимум, является частотой среза . Таким образом, параметр ε связан с полоса задерживания затухание γ в децибелы к:
Для затухания в полосе задерживания 5 дБ ε = 0,6801; для затухания 10 дБ ε = 0,3333. Частота ж0 = ω0/2π - частота среза. Частота 3 дБ жЧАС относится к ж0 к:
Полюсы и нули

Полагая, что частота среза равна единице, полюса коэффициента усиления фильтра Чебышева - нули знаменателя коэффициента усиления:
Полюса усиления фильтра Чебышева типа II являются обратными полюсам фильтра типа I:
куда м = 1, 2, ..., п . Нули фильтра Чебышева II типа - нули числителя коэффициента усиления:
Таким образом, нули фильтра Чебышева типа II являются обратными нулям многочлена Чебышева.
за м = 1, 2, ..., п.
Передаточная функция
Передаточная функция задается полюсами в левой полуплоскости функции усиления и имеет те же нули, но эти нули являются одиночными, а не двойными нулями.
Групповая задержка
Коэффициент усиления и групповая задержка для фильтра Чебышева пятого порядка типа II с ε = 0,1 показаны на графике слева. Можно видеть, что есть колебания в усилении в полосе задерживания, но не в полосе пропускания.
Выполнение
Топология Кауэра
Пассивный ЛК Чебышев фильтр нижних частот может быть реализовано с использованием Топология Кауэра. Значения индуктивности или конденсатора чебышевского n-го порядка прототип фильтра можно рассчитать по следующим уравнениям:[1]
грамм1, ГРАММk - значения конденсатора или элемента индуктивности. fЧАС, частота 3 дБ рассчитывается с помощью:
Коэффициенты А, γ, β, Аk, и Bk можно рассчитать по следующим уравнениям:
куда - пульсация полосы пропускания в децибелах. округляется от точного значения .
Расчетный граммk значения затем могут быть преобразованы в шунт конденсаторы и серии индукторы, как показано справа, или они могут быть преобразованы в последовательные конденсаторы и шунтирующие индукторы. Например,
- C1 шунт = G1, L2 серии = грамм2, ...
или же
- L1 шунт = грамм1, C1 серия = грамм2, ...
Обратите внимание, что когда G1 - шунтирующий конденсатор или последовательный индуктор, G0 соответствует входному сопротивлению или проводимости соответственно. То же соотношение верно и для Gп + 1 и Gп. Результирующая схема представляет собой нормализованный фильтр нижних частот. С помощью частотные преобразования и масштабирование импеданса, нормализованный фильтр нижних частот можно преобразовать в высокая частота, полоса пропускания, и остановка фильтры любого желаемого частота среза или же пропускная способность.
Цифровой
Как и большинство аналоговых фильтров, Чебышев может быть преобразован в цифровой (с дискретным временем) рекурсивный форма через билинейное преобразование. Однако, как цифровые фильтры имеют конечную полосу пропускания, форма отклика преобразованного Чебышева равна искривленный. В качестве альтернативы Метод согласованного Z-преобразования может использоваться, что не искажает ответ.
Сравнение с другими линейными фильтрами
На следующем рисунке показаны фильтры Чебышева рядом с другими распространенными типами фильтров, полученными с тем же числом коэффициентов (пятый порядок):
Фильтры Чебышева резче, чем Фильтр Баттерворта; они не такие острые, как эллиптический, но они показывают меньше колебаний по полосе пропускания.
Смотрите также
Примечания
Рекомендации
- ^ Matthaei et. al (1980), стр.99
- Вайнберг, Луи; Слепян, Пол (июнь 1960). «Результаты Такахаси на лестничных сетях Чебышева и Баттерворта». IRE-транзакции по теории цепей. 7 (2): 88–101. Дои:10.1109 / TCT.1960.1086643.
- Дэниэлс, Ричард В. (1974). Методы приближения для проектирования электронных фильтров. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-015308-6.
- Уильямс, Артур Б .; Тейлорс, Фред Дж. (1988). Справочник по проектированию электронных фильтров. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-070434-1.
- Matthaei, George L .; Янг, Лев; Джонс, Э. М. Т. (1980). Микроволновые фильтры, сети согласования импеданса и структуры связи. Норвуд, Массачусетс: Artech House. ISBN 0-89-006099-1.
- Лутовац, Мирослав Д. и др .: Дизайн фильтров для обработки сигналов, Прентис Холл (2001).






















































![{ displaystyle beta = ln left [ coth left ({ frac { delta} {17.37}} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/510d0b303b2f5a1fb8e4ec4aafaa780908223ec9)






