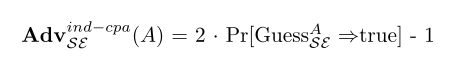WikiDer > Неразличимость зашифрованного текста

Ciphertext indistinguishability

Неразличимость зашифрованного текста это собственность многих шифрование схемы. Интуитивно, если криптосистема обладает свойством неразличимость, то противник не сможет различить пары шифртексты на основе сообщения, которое они зашифровывают. Свойство неразличимости при атака по выбранному открытому тексту считается основным требованием для большинства доказуемо безопасный криптосистемы с открытым ключом, хотя некоторые схемы также обеспечивают неразличимость атака по выбранному зашифрованному тексту и адаптивная атака по выбранному зашифрованному тексту. Неразличимость при атаке по выбранному открытому тексту эквивалентна свойству семантическая безопасность, и многие криптографические доказательства используют эти определения как синонимы.

Криптосистема считается безопасный с точки зрения неразличимости если злоумышленник с заданным шифрованием сообщения, случайно выбранным из двухэлементного пространства сообщений, определенного злоумышленником, не может идентифицировать выбор сообщения с вероятностью, значительно лучшей, чем случайное угадывание (1⁄2). Если какой-либо злоумышленник сможет различить выбранный зашифрованный текст с вероятностью значительно большей, чем1⁄2, то считается, что этот злоумышленник имеет "преимущество" в распознавании зашифрованного текста, и схема нет считается безопасным с точки зрения неразличимости. Это определение включает в себя представление о том, что в безопасной схеме злоумышленник не должен узнавать никакой информации, видя зашифрованный текст. Следовательно, противник должен иметь возможность действовать не лучше, чем если бы он угадал случайным образом.

Формальные определения

Безопасность с точки зрения неразличимости имеет множество определений в зависимости от предположений о возможностях злоумышленника. Обычно он представлен как игра, где рассматривается криптосистема безопасный если ни один противник не может выиграть игру со значительно большей вероятностью, чем противник, который должен угадать случайным образом. Наиболее распространенные определения, используемые в криптографии: неразличимость под атака по выбранному открытому тексту (сокращенно IND-CPA), неразличимость под (неадаптивная) атака по выбранному зашифрованному тексту (IND-CCA1) и неразличимость под адаптивная атака по выбранному зашифрованному тексту (IND-CCA2). Безопасность в соответствии с любым из последних определений подразумевает безопасность в соответствии с предыдущими: схема, которая является безопасным IND-CCA1, также безопасна IND-CPA, а схема, которая является безопасной IND-CCA2, является безопасной как IND-CCA1, так и IND-CPA. Таким образом, IND-CCA2 - самое сильное из трех определений безопасности.

Неразличимость при атаке с выбранным открытым текстом (IND-CPA)

Для вероятностного алгоритм шифрования с асимметричным ключом, неразличимость под атака по выбранному открытому тексту (IND-CPA) определяется следующей игрой между противником и претендентом. Для схем на основе вычислительная безопасность, противник моделируется вероятностное полиномиальное время Машина Тьюринга, что означает, что он должен завершить игру и вывести Угадай в пределах полиномиального количества временных шагов. В этом определении E (PK, M) представляет собой шифрование сообщения M под ключ ПК:

  1. Претендент генерирует пару ключей ПК, SK на основе некоторого параметра безопасности k (например, размер ключа в битах) и публикует ПК противнику. Претендент сохраняет SK.
  2. Злоумышленник может выполнять полиномиально ограниченное количество шифрований или других операций.
  3. В конце концов, противник представляет два отдельных выбранных открытых текста. претенденту.
  4. Претендент выбирает немного б {0, 1} равномерно случайным образом и отправляет испытание зашифрованный текст C = E (PK, ) обратно к противнику.
  5. Злоумышленник может выполнить любое количество дополнительных вычислений или шифрования. Наконец, он выводит предположение для значения б.

Криптосистема - это неотличим от выбранного открытого текста атаковать, если каждый вероятностно-полиномиальный противник имеет лишь незначительное "преимущество"по случайному угадыванию". Считается, что противник имеет незначительное "преимущество", если он выигрывает указанную выше игру с вероятностью , куда это незначительная функция в параметре безопасности k, то есть для любой (ненулевой) полиномиальной функции Существует такой, что для всех .

Хотя противник знает , и PK, вероятностный характер E означает, что шифрование будет только одним из многих допустимых зашифрованных текстов, поэтому шифрование , и сравнение полученных шифрованных текстов с шифрованным текстом запроса не дает злоумышленнику каких-либо существенных преимуществ.

Хотя приведенное выше определение относится к криптосистеме с асимметричным ключом, его можно адаптировать к симметричный случае, заменив функцию шифрования с открытым ключом на шифрование оракул, который сохраняет секретный ключ шифрования и шифрует произвольные открытые тексты по запросу злоумышленника.

Симметричная игра IND-CPA, формализованная

Состязательный процесс выполнения атаки по выбранному открытому тексту обычно описывается в виде Криптографическая игра. Для проверки симметричного IND-CPA определена описанная выше игра.[1] Позволять быть функцией генерации ключей, быть функцией шифрования, и быть функцией дешифрования. Позволять - симметричная схема шифрования. Игра определяется как:

IND-CPA Guess Cryptographic Game.svg

Сколько раз злоумышленник выбирает два незашифрованных сообщения по своему выбору и передает их LR oracle, который возвращает зашифрованный текст, зашифровывающий одно из сообщений. Преимущество противника определяется вероятностью угадать значение б, значение, выбранное случайным образом в начале игры, которое определяет сообщение, зашифрованное в LR оракул. Поэтому его преимущество определяется как:[1]

Преимущество IND-CPA Guess Game.svg

Неразличимость при атаке на выбранный зашифрованный текст / адаптивная атака на выбранный зашифрованный текст (IND-CCA1, IND-CCA2)

Неразличимость при неадаптивной и адаптивной атаке на выбранный зашифрованный текст (IND-CCA1, IND-CCA2) использует определение, аналогичное определению IND-CPA. Однако в дополнение к публичному ключу (или оракулу шифрования в симметричном случае) злоумышленнику предоставляется доступ к расшифровка оракула который расшифровывает произвольные зашифрованные тексты по запросу злоумышленника, возвращая открытый текст. В неадаптивном определении злоумышленнику разрешено запрашивать этот оракул только до тех пор, пока он не получит шифрованный текст запроса. В адаптивном определении злоумышленник может продолжать запрашивать оракул дешифрования даже после того, как он получил шифрованный текст запроса, с оговоркой, что он не может передать шифрованный текст запроса для дешифрования (в противном случае определение было бы тривиальным).

  1. Претендент генерирует пару ключей ПК, SK на основе некоторого параметра безопасности k (например, размер ключа в битах) и публикует ПК противнику. Претендент сохраняет SK.
  2. Злоумышленник может выполнять любое количество шифрований, вызовов оракула дешифрования на основе произвольных зашифрованных текстов или других операций.
  3. В конце концов, противник представляет два разных выбранных открытого текста. претенденту.
  4. Претендент выбирает немного б ∈ {0, 1} равномерно случайным образом и отправляет зашифрованный текст "запроса" C = E (PK, ) обратно к противнику.
  5. Злоумышленник может выполнить любое количество дополнительных вычислений или шифрования.
    1. в неадаптивный случае (IND-CCA1), противник может нет дальнейшие вызовы оракула дешифрования.
    2. в адаптивный case (IND-CCA2), злоумышленник может делать дальнейшие вызовы оракулу дешифрования, но не может отправлять шифрованный текст запроса C.
  6. Наконец, злоумышленник выдает предположение для значения б.

Схема является IND-CCA1 / IND-CCA2 безопасной, если ни один противник не имеет существенного преимущества в выигрыше в указанной выше игре.

Неотличим от случайного шума

Основная статья: Отличительная атака

Иногда нам нужны схемы шифрования, в которых строка зашифрованного текста неотличима от случайной строки злоумышленником.[2]

Если злоумышленник не может определить, существует ли сообщение, он дает человеку, написавшему сообщение правдоподобное отрицание.

Некоторые люди, создающие зашифрованные каналы связи, предпочитают делать содержимое каждой зашифрованной дейтаграммы неотличимым от случайных данных, чтобы затруднить анализ трафика.[3]

Некоторые люди, создающие системы для хранения зашифрованных данных, предпочитают, чтобы данные были неотличимы от случайных данных, чтобы сокрытие данных проще. Например, некоторые виды шифрование диска Такие как TrueCrypt попытаться скрыть данные в невинных случайных данных, оставшихся от некоторых видов стирание данныхДругой пример: некоторые виды стеганография попытаться скрыть данные, приведя их в соответствие статистическим характеристикам невинных "случайных" шум изображения в цифровых фотографиях.

Для поддержки таких отрицательное шифрование Некоторые криптографические алгоритмы специально разработаны для того, чтобы сообщения с зашифрованным текстом были неотличимы от случайных битовых строк.[4][5][6]

Большинству приложений не требуется алгоритм шифрования для создания зашифрованных сообщений, неотличимых от случайных битов. Однако некоторые авторы считают такие алгоритмы шифрования концептуально более простыми, с ними легче работать и более универсальными на практике - и большинство кодов IND-CPA алгоритмы, по-видимому, действительно создают зашифрованные сообщения, которые неотличимы от случайных битов.[7]

Эквивалентность и последствия

Неразличимость - важное свойство для сохранения конфиденциальности зашифрованных сообщений. Однако в некоторых случаях было обнаружено, что свойство неразличимости подразумевает другие, очевидно не связанные свойства безопасности. Иногда эти выводы идут в обоих направлениях, что делает два определения эквивалентными; например, известно, что свойство неразличимости при адаптивной атаке по выбранному зашифрованному тексту (IND-CCA2) эквивалентно свойству неподатливость при том же сценарии атаки (NM-CCA2). Эта эквивалентность не очевидна сразу, поскольку неизменяемость - это свойство, имеющее отношение к целостности сообщения, а не к конфиденциальности. В других случаях было продемонстрировано, что неотличимость может быть объединена с некоторыми другими определениями, чтобы подразумевать еще другие полезные определения, и наоборот. Следующий список суммирует несколько известных последствий, но отнюдь не является полным.

Обозначение означает, что свойство A влечет свойство B. означает, что свойства A и B эквивалент. означает, что свойство A не обязательно подразумевает свойство B.

Смотрите также

Рекомендации

  1. ^ а б Белларе, Михир; Рогавей, Филипп (11 мая 2005 г.). «Введение в современную криптографию, Глава 5: Симметричное шифрование» (PDF). п. 93. Получено 6 апреля 2020.
  2. ^ Чакраборти, Дебруп; Родригес-Энрикес., Франсиско (2008). Четин Кая Коч (ред.). Криптографическая инженерия. п. 340. ISBN 9780387718170.
  3. ^ iang (20 мая 2006 г.). «Не отличить от случайного». Получено 2014-08-06.
  4. ^ Бернштейн, Даниэль Дж .; Гамбург, Майк; Краснова, Анна; Ланге, Таня (2013-08-28). «Эллигатор: точки эллиптической кривой, неотличимые от однородных случайных строк» (PDF). Получено 2015-01-23.
  5. ^ Мёллер, Бодо (2004). «Схема шифрования с открытым ключом с псевдослучайными зашифрованными текстами». Компьютерная безопасность - ESORICS 2004. Конспект лекций по информатике. 3193. С. 335–351. Дои:10.1007/978-3-540-30108-0_21. ISBN 978-3-540-22987-2.
  6. ^ Мур, Кристофер; Мертенс, Стефан (2011). Природа вычислений. ISBN 9780191620805.
  7. ^ Rogaway, Филипп (2004-02-01). «Симметричное шифрование на основе nonce» (PDF). стр. 5–6. Получено 2014-08-07.