WikiDer > Криптография с открытым ключом
Эта статья нужны дополнительные цитаты для проверка. (Июль 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

Криптография с открытым ключом, или же асимметричная криптография, это криптографическая система, использующая пары ключи: открытые ключи, которые могут быть широко распространены, и приватные ключи, которые известны только владельцу. Генерация таких ключей зависит от криптографический алгоритмы на основе математический проблемы для производства односторонние функции. Эффективная безопасность требует только сохранения закрытого ключа; открытый ключ может распространяться открыто без ущерба для безопасности.[1]
В такой системе любой человек может зашифровать сообщение с использованием приемника открытый ключ, но это зашифрованное сообщение можно расшифровать только с помощью закрытый ключ. Это позволяет, например, серверу генерировать криптографический ключ, предназначенный для криптография с симметричным ключом, затем используйте открытые для общего доступа открытый ключ зашифровать этот вновь созданный симметричный ключ. Теперь сервер может отправить этот зашифрованный симметричный ключ по незащищенным каналам клиенту, и только клиент может расшифровать его, используя пару закрытых ключей клиента и открытый ключ, используемый сервером для шифрования этого сообщения. Теперь, когда клиент и сервер имеют один и тот же симметричный ключ, они могут безопасно перейти к шифрованию с симметричным ключом для безопасного обмена данными между собой по незащищенным в противном случае каналам. Это имеет то преимущество, что вам не нужно вручную делиться симметричными ключами вручную, а также дает преимущество более высокой пропускной способности данных, чем криптография с симметричным ключом по криптографии с асимметричным ключом.
С криптографией с открытым ключом, надежная аутентификация тоже возможно. Отправитель может объединить сообщение с закрытым ключом для создания короткого цифровой подписи в сообщении. Любой, у кого есть соответствующий открытый ключ отправителя, может объединить то же сообщение и предполагаемую цифровую подпись, связанную с ним, чтобы проверить, действительна ли подпись, то есть сделана владельцем соответствующего закрытого ключа.[2][3]
Алгоритмы открытых ключей - фундаментальные составляющие безопасности в современных криптосистемы, приложения и протоколы, гарантирующие конфиденциальность, подлинность и неотвратимость электронных коммуникаций и хранения данных. Они лежат в основе различных интернет-стандартов, таких как Безопасность транспортного уровня (TLS), S / MIME, PGP, и GPG. Некоторые алгоритмы открытого ключа предоставляют распределение ключей и секретность (например, Обмен ключами Диффи – Хеллмана), некоторые предоставляют цифровые подписи (например., Алгоритм цифровой подписи), а некоторые предоставляют и то, и другое (например, ЮАР). В сравнении с симметричное шифрование, асимметричное шифрование работает медленно для многих целей. Сегодняшние криптосистемы (такие как TLS, Безопасная оболочка) используют как симметричное, так и асимметричное шифрование.
Описание
До середины 1970-х годов все системы шифрования использовали алгоритмы с симметричным ключом, в котором то же криптографический ключ используется с базовым алгоритмом как отправителем, так и получателем, которые оба должны держать его в секрете. По необходимости, ключ в каждой такой системе должен был быть обменен между взаимодействующими сторонами каким-либо безопасным способом до любого использования системы - безопасный канал. Это требование никогда не бывает тривиальным и очень быстро становится неуправляемым по мере увеличения числа участников, когда безопасные каналы недоступны для обмена ключами или когда (что является разумной криптографической практикой) ключи часто меняются. В частности, если предполагается, что сообщения будут защищены от других пользователей, для каждой возможной пары пользователей требуется отдельный ключ.
Напротив, в системе открытых ключей открытые ключи могут распространяться широко и открыто, и только частный ключ должен храниться в безопасности его владельцем.
Двумя наиболее известными способами использования криптографии с открытым ключом являются:
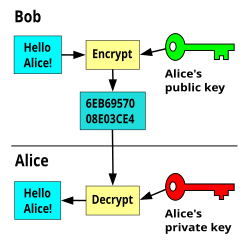
- Шифрование с открытым ключом, в котором сообщение зашифровано открытым ключом получателя. Сообщение не может быть расшифровано кем-либо, кто не обладает соответствующим закрытым ключом, который, таким образом, считается владельцем этого ключа и лицом, связанным с открытым ключом. Это используется для того, чтобы конфиденциальность.
- Цифровые подписи, в котором сообщение подписано закрытым ключом отправителя и может быть проверено любым, кто имеет доступ к открытому ключу отправителя. Эта проверка доказывает, что отправитель имел доступ к закрытому ключу и, следовательно, вероятно, был лицом, связанным с открытым ключом. Это также гарантирует, что сообщение не было подделано, поскольку подпись математически привязана к сообщению, с которым она изначально была создана, и проверка не удастся практически для любого другого сообщения, независимо от того, насколько оно похоже на исходное сообщение.
Одним из важных вопросов является уверенность / доказательство того, что конкретный открытый ключ является подлинным, т.е. что он правильный и принадлежит заявленному физическому или юридическому лицу и не был подделан или заменен злонамеренной третьей стороной. Есть несколько возможных подходов, в том числе:
А инфраструктура открытого ключа (PKI), в котором одна или несколько третьих сторон, известных как центры сертификации - подтвердить право собственности на пары ключей. TLS полагается на это.
А "сеть доверия"который децентрализует аутентификацию, используя индивидуальные подтверждения связи между пользователем и открытым ключом. PGP использует этот подход, а также поиск в система доменных имен (DNS). В DKIM Система цифровой подписи электронных писем также использует этот подход.
Приложения
Наиболее очевидное применение системы шифрования с открытым ключом - это шифрование связи для обеспечения конфиденциальность - сообщение, которое отправитель зашифровывает с использованием открытого ключа получателя, может быть расшифровано только парным закрытым ключом получателя.
Еще одно применение в криптографии с открытым ключом - это цифровой подписи. Для отправителя можно использовать схемы цифровой подписи аутентификация.
Безотказность системы используют цифровые подписи, чтобы гарантировать, что одна сторона не сможет успешно оспорить свое авторство документа или сообщения.
Другие приложения, построенные на этой основе, включают: цифровые деньги, соглашение о ключах с аутентификацией паролем, услуги отметки времени, протоколы предотвращения отказа и т. д.
Гибридные криптосистемы
Поскольку алгоритмы с асимметричным ключом почти всегда требуют больших вычислительных ресурсов, чем симметричные, во многих случаях обычно используется общедоступный / частный асимметричный алгоритм обмена ключами зашифровать и обменять симметричный ключ, затем переход к криптография с симметричным ключом для передачи данных, используя этот теперь общий симметричный ключ и алгоритм шифрования с симметричным ключом. PGP, SSH, а SSLСемейство схем / TLS использует эту процедуру и поэтому называется гибридные криптосистемы. Начальный асимметричный обмен ключами на основе криптографии для обмена сгенерированным сервером симметричный ключ от сервера к клиенту имеет то преимущество, что не требует предварительного совместного использования симметричного ключа вручную, например, на печатной бумаге или дисках, перевозимых курьером, при этом обеспечивая более высокую пропускную способность криптографии с симметричным ключом по сравнению с криптографией с асимметричным ключом для остаток от общего подключения.
Недостатки
Как и во всех системах, связанных с безопасностью, важно определить потенциальные слабые места.
Алгоритмы
Все схемы с открытым ключом теоретически подвержены "атака методом перебора ключей".[4] Однако такие атаки непрактичны, если количество вычислений, необходимых для успеха, названное «фактором работы» Клод Шеннон - недоступен для всех потенциальных злоумышленников. Во многих случаях коэффициент срабатывания можно увеличить, просто выбрав более длинный ключ. Но другие алгоритмы могут иметь гораздо более низкие рабочие факторы, что делает сопротивление атаке грубой силой несущественным. Были разработаны некоторые специальные и специфические алгоритмы, помогающие атаковать некоторые алгоритмы шифрования с открытым ключом - оба ЮАР и Шифрование Эль-Гамаля известны атаки, которые намного быстрее, чем метод грубой силы.[5]
Были обнаружены серьезные недостатки для нескольких ранее многообещающих алгоритмов с асимметричным ключом. В алгоритм "упаковки ранца" оказался небезопасным после разработки новой атаки.[6] Как и все криптографические функции, реализации с открытым ключом могут быть уязвимы для атаки по побочным каналам которые используют утечку информации для упрощения поиска секретного ключа. Ведутся исследования как для обнаружения новых атак, так и для защиты от них.
Изменение открытых ключей
Еще одна потенциальная уязвимость безопасности при использовании асимметричных ключей - это возможность атака "человек посередине", в котором передача открытых ключей перехватывается третьей стороной («человек посередине»), а затем модифицируется для предоставления вместо этого других открытых ключей. Зашифрованные сообщения и ответы также должны быть перехвачены, расшифрованы и повторно зашифрованы злоумышленником с использованием правильных открытых ключей для различных сегментов связи во всех случаях, чтобы избежать подозрений.
Связь считается небезопасной, если данные передаются способом, допускающим перехват (также называемый "нюхатьЭти термины относятся к чтению личных данных отправителя в целом. Связь особенно опасна, когда отправитель не может предотвратить или контролировать перехват.[7]
Атаку «злоумышленник посередине» сложно реализовать из-за сложности современных протоколов безопасности. Однако задача становится проще, когда отправитель использует небезопасные среды, такие как общедоступные сети, Интернет, или беспроводная связь. В этих случаях злоумышленник может поставить под угрозу инфраструктуру связи, а не сами данные. Гипотетический злонамеренный сотрудник Интернет-провайдер (Интернет-провайдер) может счесть атаку "человек посередине" относительно простой. Захват открытого ключа потребует только поиска ключа при его отправке через коммуникационное оборудование провайдера.
В некоторых сложных атаках типа «злоумышленник посередине» одна сторона коммуникации будет видеть исходные данные, а другая - вредоносный вариант. Асимметричные атаки типа «злоумышленник посередине» могут помешать пользователям понять, что их соединение скомпрометировано. Это остается верным даже в том случае, если известно, что данные одного пользователя скомпрометированы, потому что данные выглядят нормально для другого пользователя. Это может привести к запутанным разногласиям между пользователями, например, "это должно быть на вашей стороне!" когда ни один пользователь не виноват. Следовательно, атаки типа «злоумышленник посередине» можно полностью предотвратить только тогда, когда инфраструктура связи физически контролируется одной или обеими сторонами; например, по проводному маршруту в собственном здании отправителя. Таким образом, открытые ключи легче изменить, если оборудование связи, используемое отправителем, находится под контролем злоумышленника.[8][9][10]
Инфраструктура открытого ключа
Один из подходов к предотвращению таких атак включает использование инфраструктура открытого ключа (PKI); набор ролей, политик и процедур, необходимых для создания, управления, распространения, использования, хранения и отзыва цифровых сертификатов и управления шифрованием с открытым ключом. Однако это, в свою очередь, имеет потенциальные недостатки.
Например, центр сертификации, выдающий сертификат, должен быть доверенным, чтобы должным образом проверить личность держателя ключа, должен гарантировать правильность открытого ключа при выдаче сертификата, должен быть защищен от компьютерного пиратства и должен принять меры со всеми участниками, чтобы проверить все свои сертификаты перед началом защищенного обмена данными. Веб-браузеры, например, поставляются с длинным списком «самозаверяющих сертификатов идентификации» от провайдеров PKI - они используются для проверки добросовестно центра сертификации, а затем, на втором этапе, сертификаты потенциальных коммуникаторов. Злоумышленник, который может заставить любой из этих центров сертификации выдать сертификат для поддельного открытого ключа, может затем организовать атаку «человек посередине» так же легко, как если бы схема сертификата вообще не использовалась. В альтернативном сценарии редко обсуждается[нужна цитата], злоумышленник, который проникает на серверы центра и получает его хранилище сертификатов и ключей (открытых и частных), сможет без ограничений подделывать, маскировать, расшифровывать и подделывать транзакции.
Несмотря на свои теоретические и потенциальные проблемы, этот подход широко используется. Примеры включают TLS и его предшественник SSL, которые обычно используются для обеспечения безопасности транзакций в веб-браузере (например, для безопасной отправки данных кредитной карты в интернет-магазин).
Помимо устойчивости к атакам конкретной пары ключей, безопасность сертификации иерархия необходимо учитывать при развертывании систем с открытым ключом. Некоторые центры сертификации - обычно это специализированная программа, работающая на сервере, - гарантируют идентификационные данные, присвоенные конкретным закрытым ключам, путем создания цифрового сертификата. Цифровые сертификаты открытого ключа обычно действительны в течение нескольких лет, поэтому связанные закрытые ключи должны надежно храниться в течение этого времени. Когда закрытый ключ, используемый для создания сертификата выше в иерархии PKI-сервера, скомпрометирован или случайно раскрыт, то появляется "атака "человек посередине""возможно, что делает любой подчиненный сертификат полностью небезопасным.
Примеры
Примеры хорошо зарекомендовавших себя техник асимметричного ключа для различных целей:
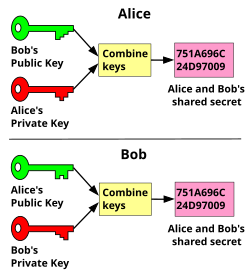
- Обмен ключами Диффи – Хеллмана протокол
- DSS (стандарт цифровой подписи), который включает Алгоритм цифровой подписи
- Эль-Гамаль
- Криптография с эллиптической кривой
- Разные соглашение о ключах с аутентификацией паролем техники
- Криптосистема Пайе
- ЮАР алгоритм шифрования (PKCS # 1)
- Криптосистема Крамера – Шупа
- ЯК протокол согласования аутентифицированного ключа
Примеры алгоритмов с асимметричным ключом, которые не получили широкого распространения, включают:
- NTRUEncrypt криптосистема
- Криптосистема Мак-Элиса
Примеры заметных, но небезопасных алгоритмов асимметричного ключа включают:
Примеры протоколов, использующих алгоритмы асимметричного ключа, включают:
- S / MIME
- GPG, реализация OpenPGP
- EMV, Центр сертификации EMV
- IPsec
- PGP
- ZRTP, безопасный VoIP протокол
- Безопасность транспортного уровня стандартизировано IETF и его предшественник Уровень защищенных сокетов
- SILC
- SSH
- Биткойн
- Сообщения без записи
История
В начале история криптографии, две стороны будут полагаться на ключ, которым они будут обмениваться с помощью безопасного, но не криптографического метода, такого как личная встреча или доверенный курьер. Этот ключ, который обе стороны держали в абсолютном секрете, затем можно было использовать для обмена зашифрованными сообщениями. При таком подходе к раздача ключей.
Ожидание
В своей книге 1874 года Принципы науки, Уильям Стэнли Джевонс[11] написал:
Может ли читатель сказать, какие два числа, умноженные вместе, дают число? 8616460799?[12] Думаю, вряд ли кто-нибудь, кроме меня, когда-нибудь узнает.[13]
Здесь он описал отношения односторонние функции криптографии, и продолжил обсуждение конкретно факторизация проблема используется для создания функция люка. В июле 1996 г. математик Соломон В. Голомб сказал: «Джевонс предвидел ключевую особенность алгоритма RSA для криптографии с открытым ключом, хотя, конечно, он не изобретал концепцию криптографии с открытым ключом».[14]
Секретное открытие
В 1970 г. Джеймс Х. Эллис, британский криптограф из Великобритании Штаб правительственной связи (GCHQ), предполагал возможность «несекретного шифрования» (теперь называемого криптографией с открытым ключом), но не видел способа его реализовать.[15] В 1973 году его коллега Клиффорд Кокс реализовал то, что стало известно как Алгоритм шифрования RSA, предложив практический метод «несекретного шифрования», а в 1974 году другой математик и криптограф из GCHQ, Малькольм Дж. Уильямсон, разработал то, что сейчас известно как Обмен ключами Диффи – Хеллмана. Схема также была передана в США. Национальное Агенство Безопасности.[16] С военной направленностью и низкой вычислительной мощностью мощь криптографии с открытым ключом не была реализована в обеих организациях:
Я счел его наиболее важным для использования в военных целях ... если вы можете быстро и в электронном виде поделиться своим ключом, у вас будет большое преимущество перед противником. Только в конце эволюции от Бернерс-Ли разработка открытой интернет-архитектуры для ЦЕРН, его адаптация и принятие для Арпанет ... реализовала ли криптография с открытым ключом весь свой потенциал.
Их открытие не было публично признано в течение 27 лет, пока британское правительство не рассекретило исследование в 1997 году.[17]
Публичное открытие
В 1976 году криптосистема с асимметричным ключом была опубликована Уитфилд Диффи и Мартин Хеллман кто под влиянием Ральф МерклРабота над распространением открытых ключей раскрыла метод согласования открытых ключей. Это метод обмена ключами, который использует возведение в степень в конечном поле, стал известен как Обмен ключами Диффи – Хеллмана.[18] Это был первый опубликованный практический метод установления общего секретного ключа по проверенному (но не конфиденциальному) каналу связи без использования предварительного общего секрета. «Методика согласования открытых ключей» Меркла стала известна как Пазлы Меркла, и был изобретен в 1974 году и опубликован в 1978 году.
В 1977 г. было независимо изобретено обобщение схемы Кокса. Рон Ривест, Ади Шамир и Леонард Адлеман, все тогда в Массачусетский технологический институт. Последние авторы опубликовали свою работу в 1978 году, и алгоритм стал известен как ЮАР, от их инициалов.[19] RSA использует возведение в степень по модулю продукт двух очень больших простые числа, для шифрования и дешифрования, выполняя как шифрование с открытым ключом, так и цифровую подпись с открытым ключом. Его безопасность связана с чрезвычайной сложностью факторизация больших целых чисел, проблема, для которой не существует известной эффективной общей техники (хотя простая факторизация может быть получена с помощью атак грубой силы; это может быть сложнее, чем больше простые множители). Описание алгоритма опубликовано в Математические игры в августовском выпуске 1977 г. Scientific American.[20]
С 1970-х годов в области криптографии с открытым ключом было разработано большое количество разнообразных методов шифрования, цифровой подписи, согласования ключей и других методов, включая Криптосистема Рабина, Шифрование Эль-Гамаля, DSA - и криптография на основе эллиптических кривых.
Смотрите также
- Книги по криптографии
- GNU Privacy Guard
- Шифрование на основе идентификатора (МБП)
- Ключ условное депонирование
- Протокол согласования ключей
- Список слов PGP
- Довольно хорошая конфиденциальность
- Псевдонимность
- Отпечаток открытого ключа
- Инфраструктура открытого ключа (PKI)
- Квантовые вычисления
- Квантовая криптография
- Безопасная оболочка (SSH)
- Безопасность транспортного уровня (TLS)
- Алгоритм с симметричным ключом
- Пороговая криптосистема
- Сеть доверия
Примечания
- ^ Столлингс, Уильям (3 мая 1990 г.). Криптография и сетевая безопасность: принципы и практика. Прентис Холл. п. 165. ISBN 9780138690175.
- ^ Альфред Дж. Менезес, Пол К. ван Оршот и Скотт А. Ванстон (октябрь 1996 г.). «11: Цифровые подписи» (PDF). Справочник по прикладной криптографии. CRC Press. ISBN 0-8493-8523-7. Получено 14 ноября 2016.CS1 maint: использует параметр авторов (связь)
- ^ Дэниел Дж. Бернштейн (1 мая 2008 г.). «Защита сообщений от подделки» (PDF). Алгоритмическая теория чисел. 44. Публикации ИИГС. §5: Подписи с открытым ключом, стр. 543–545. Получено 14 ноября 2016.
- ^ Паар, Кристоф; Пельцль, Ян; Пренил, Барт (2010). Понимание криптографии: учебник для студентов и практиков. Springer. ISBN 978-3-642-04100-6.
- ^ Мавроэйдис, Василиос и Камер Виши, «Влияние квантовых вычислений на современную криптографию», Международный журнал передовых компьютерных наук и приложений, 31 марта 2018
- ^ Шамир, Ади; Шамир, Ади; Шамир, Ади; Шамир, Ади (ноябрь 1982 г.). «Алгоритм с полиномиальным временем для взлома базовой криптосистемы Меркла-Хеллмана». 23-й ежегодный симпозиум по основам компьютерных наук (SFCS 1982): 145–152. Дои:10.1109 / SFCS.1982.5.
- ^ Тунггал, Аби (20 февраля 2020 г.). «Что такое атака« человек посередине »и как ее предотвратить - в чем разница между атакой« человек посередине »и обнюхиванием?». UpGuard. Получено 26 июн 2020.
- ^ Тунггал, Аби (20 февраля 2020 г.). «Что такое атака« человек посередине »и как ее предотвратить - где происходят атаки« злоумышленник посередине »?». UpGuard. Получено 26 июн 2020.
- ^ Мартин (30 января 2013 г.). "Китай, GitHub и человек посередине". Большой пожар. В архиве с оригинала 19 августа 2016 г.. Получено 27 июн 2015.
- ^ Перси (4 сентября 2014 г.). "Власти запускают атаку" человек посередине "на Google". Большой пожар. Получено 26 июн 2020.
- ^ Джевонс, Уильям Стэнли, Принципы науки: трактат по логике и научному методу п. 141, Macmillan & Co., Лондон, 1874 г., 2-е изд. 1877 г., 3-е изд. 1879. Перепечатано с предисловием. Эрнст Нагель, Dover Publications, Нью-Йорк, Нью-Йорк, 1958.
- ^ Это стало известно как «число Джевонса». Единственная нетривиальная факторная пара - 89681 × 96079.
- ^ Принципы науки, Macmillan & Co., 1874, стр. 141.
- ^ Голоб, Соломон В. (1996). "О факторинге числа Джевонса". Криптология. 20 (3): 243. Дои:10.1080/0161-119691884933. S2CID 205488749.
- ^ Савер, Патрик (11 марта 2016 г.). «Незаметный гений, который обеспечил британскую компьютерную защиту и подготовил почву для безопасных покупок в Интернете». Телеграф.
- ^ а б Том Эспинер (26 октября 2010 г.). «Пионеры GCHQ в рождении криптографии с открытым ключом». www.zdnet.com.
- ^ Сингх, Саймон (1999). Кодовая книга. Doubleday. стр.279–292.
- ^ Диффи, Уитфилд; Хеллман, Мартин Э. (Ноябрь 1976 г.). «Новые направления в криптографии» (PDF). IEEE Transactions по теории информации. 22 (6): 644–654. CiteSeerX 10.1.1.37.9720. Дои:10.1109 / TIT.1976.1055638. В архиве (PDF) из оригинала от 29 ноября 2014 г.
- ^ Ривест, Р .; Шамир, А .; Адлеман, Л. (февраль 1978 г.). «Метод получения цифровых подписей и криптосистем с открытым ключом» (PDF). Коммуникации ACM. 21 (2): 120–126. CiteSeerX 10.1.1.607.2677. Дои:10.1145/359340.359342. S2CID 2873616.
- ^ Робинсон, Сара (июнь 2003 г.). «По-прежнему храня секреты после многих лет атак, RSA заслуживает похвалы для своих основателей» (PDF). Новости SIAM. 36 (5).
Рекомендации
- Хирш, Фредерик Дж. «Надежное шифрование SSL / TLS: Введение». HTTP-сервер Apache. Получено 17 апреля 2013.. Первые два раздела содержат очень хорошее введение в криптографию с открытым ключом.
- Фергюсон, Нильс; Шнайер, Брюс (2003). Практическая криптография. Wiley. ISBN 0-471-22357-3.
- Кац, Джон; Линделл Ю. (2007). Введение в современную криптографию. CRC Press. ISBN 978-1-58488-551-1.
- Менезеш, А. Дж.; van Oorschot, P.C .; Ванстон, Скотт А. (1997). Справочник по прикладной криптографии. ISBN 0-8493-8523-7.
- IEEE 1363: Стандартные спецификации для криптографии с открытым ключом
- Кристоф Паар, Ян Пельцль, «Введение в криптографию с открытым ключом», Глава 6 «Понимание криптографии, Учебник для студентов и практиков». (сопутствующий веб-сайт содержит онлайн-курс по криптографии, который охватывает криптографию с открытым ключом), Springer, 2009.
внешняя ссылка
- Устное историческое интервью с Мартином Хеллманом, Институт Чарльза Бэббиджа, Университет Миннесоты. Ведущий специалист по криптографии Мартин Хеллман обсуждает с сотрудниками обстоятельства и фундаментальные идеи своего изобретения криптографии с открытым ключом Уитфилд Диффи и Ральф Меркл в Стэнфордском университете в середине 1970-х.
- Отчет о том, как GCHQ держал свое изобретение PKE в секрете до 1997 года.