WikiDer > Лестница космических расстояний
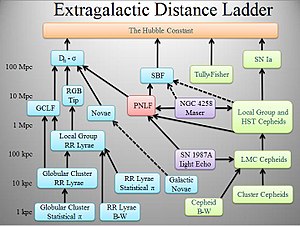
- Светло-зеленые квадраты: метод, применимый к звездообразующие галактики.
- Светло-синие коробки: метод, применимый к Население II галактики.
- Светло-фиолетовые коробки: техника геометрической дистанции.
- Светло-красная коробка: функция светимости планетарной туманности метод применим ко всем популяциям Сверхскопление Девы.
- Сплошные черные линии: хорошо откалиброванная ступенька.
- Пунктирные черные линии: ступенька лестницы неопределенной калибровки.
В космическая дистанционная лестница (также известный как шкала внегалактических расстояний) - последовательность методов, с помощью которых астрономы определить расстояния к небесным объектам. Настоящая непосредственный измерение расстояния до астрономического объекта возможно только для тех объектов, которые находятся «достаточно близко» (в пределах примерно тысячи парсек) на Землю. Все методы определения расстояний до более удаленных объектов основаны на различных измеренных корреляциях между методами, которые работают на близких расстояниях, и методами, которые работают на больших расстояниях. Некоторые методы полагаются на стандартная свеча, который представляет собой астрономический объект, известный яркость.
Аналогия с лестницей возникает потому, что ни один метод не может измерить расстояния на всех диапазонах, встречающихся в астрономии. Вместо этого можно использовать один метод для измерения ближайших расстояний, второй - для измерения ближайших и промежуточных расстояний и так далее. Каждая ступенька лестницы предоставляет информацию, которую можно использовать для определения расстояний на следующей более высокой ступеньке.
Прямое измерение

У основания лестницы находятся фундаментальный измерения расстояний, при которых расстояния определяются напрямую, без каких-либо физических предположений о природе рассматриваемого объекта. Точное измерение положения звезд является частью дисциплины астрометрия.
Астрономическая единица
Прямые измерения расстояния основаны на астрономическая единица (AU), которое определяется как среднее расстояние между земной шар и солнце.Законы Кеплера обеспечить точный соотношения размеров орбит объектов, вращающихся вокруг Солнца, но не дает измерения общего масштаба орбитальной системы. Радар используется для измерения расстояния между орбитами Земли и второго тела. На основе этого измерения и соотношения двух размеров орбиты вычисляется размер орбиты Земли. Орбита Земли известна с абсолютной точностью до нескольких метров и относительной точностью до нескольких долей в 100 миллиардов (1×10−11).
Исторически сложилось так, что наблюдения транзиты Венеры имели решающее значение в определении AU; в первой половине ХХ века наблюдения за астероиды также были важны. В настоящее время орбита Земли определяется с высокой точностью с помощью радар измерения расстояний до Венера и другие близлежащие планеты и астероиды,[1] и отслеживая межпланетные космический корабль на своих орбитах вокруг Солнца через Солнечная система.
Параллакс
Наиболее важные фундаментальные измерения расстояния прибывают из тригонометрических параллакс. По мере того, как Земля вращается вокруг Солнца, положение ближайших звезд будет немного сдвигаться на более отдаленном фоне. Эти сдвиги представляют собой равнобедренные углы. треугольник, с 2 Австралия (расстояние между крайними положениями орбиты Земли вокруг Солнца), составляющее основание треугольника, а расстояние до звезды - длинные ноги равной длины. Величина сдвига довольно небольшая, составляет 1 угловая секунда для объекта на 1парсекрасстояние (3,26 световых лет) ближайших звезд, а затем уменьшаются по угловому значению с увеличением расстояния. Астрономы обычно выражают расстояния в парсеках (угловые секунды параллакса); световые годы используются в популярных средствах массовой информации.
Поскольку параллакс становится меньше с увеличением расстояния до звезды, полезные расстояния можно измерить только для звезд, которые находятся достаточно близко, чтобы иметь параллакс, превышающий в несколько раз точность измерения. Например, в 1990-е гг. Hipparcos миссия получила параллаксы для более чем ста тысяч звезд с точностью около миллисекунда дуги,[2] обеспечивая полезные расстояния для звезд до нескольких сотен парсеков. Телескоп Хаббла WFC3 теперь имеет потенциал обеспечить точность от 20 до 40 микроугловые секунды, что позволяет надежно измерять расстояние до 5 000 парсек (16 000 световых лет) для небольшого количества звезд.[3][4] В 2018 году выпуск данных 2 из Гайя космическая миссия обеспечивает одинаково точные расстояния до большинства звезд ярче 15-й величины.[5]
Скорость звезд относительно Солнца вызывает правильное движение (поперек неба) и радиальная скорость (движение к Солнцу или от него). Первое определяется путем построения графика изменения положения звезд на протяжении многих лет, а второе - путем измерения Доплеровский сдвиг спектра звезды, вызванного движением вдоль луча зрения. Для группы звезд с одинаковым спектральным классом и аналогичным диапазоном звездных величин средний параллакс может быть получен из статистический анализ собственных движений относительно их лучевых скоростей. Этот статистический параллакс Метод полезен для измерения расстояний до ярких звезд свыше 50 парсеков и гигантских переменные звезды, в том числе Цефеиды и Переменные RR Лиры.[6]

Движение Солнца в космосе обеспечивает более длинную базовую линию, которая увеличит точность измерений параллакса, известную как светский параллакс. Для звезд в диске Млечного Пути это соответствует средней базе 4 Австралия в год, в то время как для звезд гало базовый уровень составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на несколько порядков больше, чем базовая линия Земля – Солнце, используемая для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость наблюдаемых звезд является дополнительной неизвестной. Применительно к выборкам из нескольких звезд неопределенность может быть уменьшена; неопределенность обратно пропорциональна квадратный корень размера выборки.[9]
Параллакс движущегося кластера - это метод, с помощью которого движения отдельных звезд в соседнем звездном скоплении можно использовать для определения расстояния до скопления. Только открытые кластеры достаточно близки, чтобы использовать эту технику. В частности, расстояние, полученное для Гиады исторически был важным шагом на пути к дистанционной лестнице.
Для других отдельных объектов могут быть сделаны фундаментальные оценки расстояния при определенных обстоятельствах. Если расширение газового облака, как остаток сверхновой или планетарная туманность, можно наблюдать с течением времени, то параллакс расширения расстояние до этого облака можно оценить. Однако эти измерения страдают от неточностей в отклонении объекта от сферичности. Бинарные звезды которые оба визуальный и спектроскопический расстояние между двоичными объектами также можно оценить аналогичным образом, и они не страдают от вышеуказанной геометрической неопределенности. Общей характеристикой этих методов является то, что измерение углового движения сочетается с измерением абсолютного скорость (обычно получается через Эффект Допплера). Оценка расстояния получается из расчета того, как далеко должен быть объект, чтобы его наблюдаемая абсолютная скорость соответствовала наблюдаемому угловому движению.
Параллаксы расширения, в частности, могут дать фундаментальные оценки расстояний для очень далеких объектов, потому что выбросы сверхновых имеют большие скорости расширения и большие размеры (по сравнению со звездами). Далее их можно наблюдать по радио. интерферометры который может измерять очень малые угловые движения. Все это вместе дает фундаментальные оценки расстояний до сверхновых в других галактиках.[10] Несмотря на свою ценность, такие случаи довольно редки, поэтому они служат важными проверками согласованности на дистанционной лестнице, а не сами по себе ступеньками рабочей лошадки.
Стандартные свечи
Почти все астрономические объекты, используемые в качестве индикаторов физического расстояния, относятся к классу с известной яркостью. Сравнивая это известное яркость к наблюдаемой яркости объекта, расстояние до объекта можно вычислить с помощью закон обратных квадратов. Эти объекты известной яркости называются стандартные свечи, придуманный Генриетта Суон Ливитт.[11]
Яркость объекта можно выразить через его абсолютная величина. Эта величина получается из логарифма его светимости, если смотреть с расстояния 10 парсек. В кажущаяся величина, величина, которую видит наблюдатель (инструмент, называемый болометр используется), может быть измерен и использован с абсолютной величиной для расчета расстояния d к объекту в парсеках[12] следующим образом:
или
где м - видимая величина, а M абсолютная величина. Чтобы это было точным, обе величины должны быть в одной полосе частот, и не может быть относительного движения в радиальном направлении.
Некоторые способы коррекции межзвездного вымирание, что также делает объекты более тусклыми и красными, особенно если объект находится в пыльной или газообразной области.[13] Разница между абсолютной и видимой величинами объекта называется его величиной. модуль расстояния, и астрономические расстояния, особенно межгалактические, иногда табулируются таким образом.
Проблемы
Для стандартных свечей любого класса существуют две проблемы. Главный из них калибровка, то есть точное определение абсолютной величины свечи. Это включает в себя определение класса достаточно хорошо, чтобы члены могли быть распознаны, и поиск достаточного количества членов этого класса с хорошо известными расстояниями, чтобы их истинная абсолютная величина могла быть определена с достаточной точностью. Вторая проблема заключается в распознавании членов класса, а не в использовании по ошибке стандартной калибровки свечи на объекте, не принадлежащем к этому классу. На экстремальных расстояниях, где больше всего желательно использовать индикатор расстояния, эта проблема распознавания может быть довольно серьезной.
Существенной проблемой стандартных свечей является повторяющийся вопрос, насколько они стандартны. Например, все наблюдения показывают, что Сверхновые типа Ia которые находятся на известном расстоянии, имеют одинаковую яркость (с поправкой на форму кривой блеска). Основание этой близости по яркости обсуждается ниже; однако существует вероятность того, что далекие сверхновые типа Ia имеют свойства, отличные от свойств близких сверхновых типа Ia. Использование сверхновых типа Ia имеет решающее значение для определения правильного космологическая модель. Если действительно свойства сверхновых типа Ia различны на больших расстояниях, то есть если экстраполяция их калибровки на произвольные расстояния недействительна, игнорирование этого изменения может опасно исказить реконструкцию космологических параметров, в частности реконструкцию материи. параметр плотности.[14][требуется разъяснение]
То, что это не просто философский вопрос, можно увидеть из истории измерения расстояний, используя Цефеид переменные. В 1950-х годах Вальтер Бааде обнаружил, что близкие переменные цефеид, используемые для калибровки стандартной свечи, были другого типа, чем те, которые используются для измерения расстояний до ближайших галактик. Ближайшие переменные цефеид были население I звезды с гораздо более высокими металл содержание, чем далекие население II звезды. В результате звезды популяции II были намного ярче, чем предполагалось, и после корректировки это привело к удвоению расстояний до шаровых скоплений, ближайших галактик и диаметра звездных скоплений. Млечный Путь.
Стандартная сирена
Гравитационные волны происходящий из инспиральная фаза компактных двойных систем, таких как нейтронные звезды или черные дыры, обладают тем полезным свойством, что энергия, излучаемая как гравитационное излучение, исходит исключительно от орбитальная энергия пары, и результирующее сокращение их орбит непосредственно наблюдается как увеличение частоты излучаемых гравитационных волн. К ведущий заказ, то скорость изменения частоты дан кем-то[15][16]:38
где это гравитационная постоянная, это скорость света, и является единственной (следовательно, вычислимой[а]) номер называется щебетать масса системы, сочетание масс из двух объектов[18]
Наблюдая за формой волны, можно вычислить массу щебета и, следовательно, мощность (скорость излучения энергии) гравитационных волн. Таким образом, такой источник гравитационных волн является стандартная сирена известной громкости.[19][16]
Как и в случае со стандартными свечами, с учетом излучаемых и принимаемых амплитуд закон обратных квадратов определяет расстояние до источника. Однако есть некоторые отличия от стандартных свечей. Гравитационные волны не изотропно излучаются, но измерение поляризации волны дает достаточно информации, чтобы определить угол излучения. Детекторы гравитационных волн также имеют анизотропные диаграммы направленности антенны, поэтому положение источника на небе относительно детекторов необходимо для определения угла приема. Обычно, если волна обнаруживается сетью из трех детекторов в разных местах, сеть будет измерять достаточно информации, чтобы внести эти поправки и получить расстояние. Также, в отличие от стандартных свечей, гравитационные волны не нуждаются в калибровке по другим параметрам расстояния. Измерение расстояния, конечно, требует калибровки детекторов гравитационных волн, но тогда расстояние в основном задается как кратное длине волны лазерного света, используемого в гравитационно-волновой интерферометр.
Есть и другие факторы, ограничивающие точность этого расстояния, помимо калибровки детектора. К счастью, гравитационные волны не подвержены влиянию вымирание из-за промежуточной поглощающей среды. Но они находятся при условии гравитационное линзирование, так же, как и свет. Если сигнал сильно линзированный, то он может быть получен как несколько событий, разделенных во времени (например, аналог нескольких изображений квазара). Менее легко распознать и контролировать эффект слабое линзирование, где на путь сигнала в пространстве влияет множество событий небольшого увеличения и уменьшения. Это будет важно для сигналов, исходящих от космологической красные смещения больше 1. Наконец, детекторным сетям сложно точно измерить поляризацию сигнала, если двоичная система наблюдается почти лицом к лицу;[20] такие сигналы имеют значительно большие ошибки при измерении расстояния. К сожалению, двойные системы излучают наиболее сильно перпендикулярно плоскости орбиты, поэтому сигналы «лицом к лицу» по своей природе сильнее и чаще всего наблюдаются.
Если двойная система состоит из пары нейтронных звезд, их слияние будет сопровождаться килонова/гиперновая взрыв, который может позволить точно определить местоположение с помощью электромагнитных телескопов. В таких случаях красное смещение родительской галактики позволяет определить Постоянная Хаббла .[18] Так было для GW170817, который был использован для проведения первого такого измерения.[21] Даже если не удается идентифицировать электромагнитный аналог для ансамбля сигналов, можно использовать статистический метод, чтобы вывести значение .[18]
Стандартная линейка
Другой класс индикаторов физического расстояния - это стандартная линейка. В 2008 г. диаметры галактик были предложены в качестве возможной стандартной линейки для определения космологических параметров.[22] Совсем недавно физический масштаб, запечатленный барионные акустические колебания (BAO) в ранней вселенной. В ранней вселенной (до рекомбинация) барионы и фотоны рассеиваются друг от друга и образуют прочно связанную жидкость, которая может поддерживать звуковые волны. Волны возникают из-за первичных возмущений плотности и движутся со скоростью, которую можно предсказать, исходя из плотности барионов и других космологических параметров. Общее расстояние, которое эти звуковые волны могут пройти до рекомбинации, определяет фиксированный масштаб, который просто расширяется вместе со Вселенной после рекомбинации. Таким образом, BAO представляет собой стандартную линейку, которую можно измерить в обзорах галактик по влиянию барионов на кластеризацию галактик. Этот метод требует обширного обзора галактик, чтобы сделать эту шкалу видимой, но он был измерен с точностью до процента (см. барионные акустические колебания). Масштаб действительно зависит от космологических параметров, таких как плотность барионов и материи, а также количество нейтрино, поэтому расстояния, основанные на BAO, больше зависят от космологической модели, чем расстояния, основанные на локальных измерениях.
Световое эхо также могут использоваться как стандартные линейки,[23][24] хотя сложно правильно измерить исходную геометрию.[25][26]
Индикаторы галактического расстояния
За некоторыми исключениями, расстояния, основанные на прямых измерениях, доступны только примерно до тысячи парсеков, что составляет небольшую часть нашей Галактики. Для расстояний, превышающих это, меры зависят от физических допущений, то есть от утверждения, что человек распознает рассматриваемый объект, и класс объектов достаточно однороден, чтобы его элементы можно было использовать для значимой оценки расстояния.
Индикаторы физического расстояния, используемые на все более крупных шкалах расстояний, включают:
- Динамический параллакс, использует орбитальные параметры визуальные двоичные файлы для измерения массы системы и, следовательно, использовать соотношение масса – светимость для определения светимости
- Затменные двоичные файлы - В последнее десятилетие измерения фундаментальных параметров затменных двойных систем стали возможны с помощью телескопов 8-метрового класса. Это позволяет использовать их как индикаторы расстояния. Недавно они использовались для получения прямых оценок расстояния до Большое Магелланово Облако (LMC), Малое Магелланово Облако (SMC), Галактика Андромеды и Галактика Треугольник. Затменные двойные системы предлагают прямой метод измерения расстояния до галактик с новым улучшенным уровнем точности 5%, который возможен с помощью современных технологий на расстоянии около 3 Мпк (3 миллиона парсеков).[27]
- Переменные RR Лиры - используется для измерения расстояний в пределах галактика и поблизости шаровые скопления.
- Все следующие четыре индикатора используют звезды в старых звездных популяциях (Население II):[28]
- Кончик ветви красного гиганта (TRGB) индикатор расстояния.
- Функция светимости планетарной туманности (PNLF)
- Функция светимости шарового скопления (GCLF)
- Колебания яркости поверхности (SBF)
- В галактической астрономии Рентгеновские вспышки (термоядерные вспышки на поверхности нейтронная звезда) используются как стандартные свечи. Наблюдения за рентгеновскими вспышками иногда показывают рентгеновские спектры, указывающие на расширение радиуса. Следовательно, поток рентгеновского излучения на пике всплеска должен соответствовать Светимость Эддингтона, который можно вычислить, если известна масса нейтронной звезды (обычно используется предположение 1,5 массы Солнца). Этот метод позволяет определять расстояние до некоторых маломассивных Рентгеновские двойные системы. Рентгеновские двойные системы с малой массой очень тусклые в оптическом отношении, что затрудняет определение расстояний до них.
- Межзвездные мазеры может использоваться для определения расстояний до галактических и некоторых внегалактических объектов, которые имеют мазерное излучение.
- Цефеиды и новые
- В Соотношение Талли – Фишера
- В Соотношение Фабера – Джексона
- Сверхновые типа Ia которые имеют очень хорошо определенную максимальную абсолютную величину как функцию формы их кривая блеска и полезны для определения внегалактических расстояний до нескольких сотен Мпк.[29] Заметным исключением является SN 2003fg, "Сверхновая звезда шампанского", сверхновая звезда типа Ia необычной природы.
- Красные смещения и Закон Хаббла
Подгонка основной последовательности
Когда абсолютная звездная величина для группы звезд наносится на график против спектральная классификация звезды, в Диаграмма Герцшпрунга – Рассела, обнаружены закономерности эволюции, которые связаны с массой, возрастом и составом звезды. В частности, в период горения водорода звезды лежат вдоль кривой на диаграмме, называемой главная последовательность. Измеряя эти свойства по спектру звезды, можно определить положение звезды главной последовательности на диаграмме H – R и, таким образом, оценить абсолютную величину звезды. Сравнение этого значения с видимой звездной величиной позволяет определить приблизительное расстояние после поправки на межзвездное расстояние. вымирание светимости из-за газа и пыли.
В гравитационно связанном звездное скопление такой как Гиады, звезды сформировались примерно одного возраста и расположены на одинаковом расстоянии. Это позволяет относительно точно подобрать основную последовательность, обеспечивая определение возраста и расстояния.
Шкала внегалактических расстояний
| Метод | Неопределенность для одиночной галактики (mag) | Расстояние до Скопление Девы (Мпк) | Диапазон (Мпк) |
|---|---|---|---|
| Классические цефеиды | 0.16 | 15–25 | 29 |
| Novae | 0.4 | 21.1 ± 3.9 | 20 |
| Функция светимости планетарной туманности | 0.3 | 15.4 ± 1.1 | 50 |
| Функция светимости шарового скопления | 0.4 | 18.8 ± 3.8 | 50 |
| Колебания яркости поверхности | 0.3 | 15.9 ± 0.9 | 50 |
| Отношение сигма-D | 0.5 | 16.8 ± 2.4 | > 100 |
| Сверхновые типа Ia | 0.10 | 19.4 ± 5.0 | > 1000 |
Шкала внегалактических расстояний - это серия методов, используемых сегодня астрономами для определения расстояния до космологических тел за пределами нашей галактики, которые нелегко получить традиционными методами. Некоторые процедуры используют свойства этих объектов, например звезды, шаровые скопления, туманности, и галактики в целом. Другие методы больше основаны на статистике и вероятностях таких вещей, как целые скопления галактик.
Эффект Вильсона – Баппу
Открыт в 1956 г. Олин Уилсон и М.К. Вайну Баппу, то Эффект Вильсона – Баппу использует эффект, известный как спектроскопический параллакс. Многие звезды имеют особенности в своих спектры, такой как кальций K-line, которые указывают на их абсолютная величина. Затем расстояние до звезды можно рассчитать по ее кажущаяся величина с использованием модуль расстояния.
Этот метод определения расстояний до звезд имеет серьезные ограничения. Калибровка силы спектральных линий имеет ограниченную точность и требует поправки на межзвездное вымирание. Хотя теоретически этот метод может обеспечить надежные расчеты расстояний до звезд размером до 7 мегапарсеков (Мпк), он обычно используется только для звезд размером в сотни килопарсек (кпк).
Классические цефеиды
За пределами досягаемости Эффект Вильсона – Баппу, следующий метод полагается на соотношение период-светимость классических Цефеида переменная звезды. Следующее соотношение можно использовать для расчета расстояния до галактических и внегалактических классических цефеид:
Несколько проблем усложняют использование цефеид в качестве стандартных свечей и активно обсуждаются, главными из них являются: природа и линейность зависимости периода от светимости в различных полосах пропускания и влияние металличности как на нулевую точку, так и на наклон этих отношений. и влияние фотометрического загрязнения (смешения) и меняющегося (обычно неизвестного) закона вымирания на расстояниях между цефеидами.[33][34][35][36][37][38][39][40][41]
Эти нерешенные вопросы привели к указанным значениям для Постоянная Хаббла в диапазоне от 60 км / с / Мпк до 80 км / с / Мпк. Устранение этого несоответствия - одна из важнейших проблем астрономии, поскольку некоторые космологические параметры Вселенной могут быть значительно лучше ограничены путем предоставления точного значения постоянной Хаббла.[42][43]
Цефеиды переменных звезд были ключевым инструментом в заключении Эдвина Хаббла 1923 года о том, что M31 (Андромеда) была внешней галактикой, в отличие от меньшей туманности внутри Млечный Путь. Он смог рассчитать расстояние от M31 до 285 кпк, сегодняшнее значение составляет 770 кпк.
Как было обнаружено на данный момент, NGC 3370, спиральная галактика в созвездии Льва, содержит самые дальние цефеиды, обнаруженные на расстоянии 29 Мпк. Переменные звезды-цефеиды никоим образом не являются идеальными маркерами расстояний: у ближайших галактик они имеют ошибку около 7% и до 15% ошибки для самых далеких.
Сверхновые
Есть несколько различных методов, для которых сверхновые может быть использован для измерения внегалактических расстояний.
Измерение фотосферы сверхновой
Можно предположить, что сверхновая расширяется сферически симметрично. Если сверхновая находится достаточно близко, так что мы можем измерить угловую протяженность, θ(т), своего фотосфера, мы можем использовать уравнение
где ω угловая скорость, θ угловая протяженность. Чтобы получить точное измерение, необходимо провести два наблюдения, разделенных временем Δт. Впоследствии мы можем использовать
где d - расстояние до сверхновой, Vэдж - лучевая скорость выброса сверхновой (можно предположить, что Vэдж равно Vθ если сферически симметричный).
Этот метод работает, только если сверхновая находится достаточно близко, чтобы можно было точно измерить фотосферу. Точно так же расширяющаяся газовая оболочка на самом деле не является ни идеально сферической, ни идеальным черным телом. Также межзвездное поглощение может помешать точным измерениям фотосферы. Эта проблема еще больше усугубляется сверхновой с коллапсом ядра. Все эти факторы приводят к ошибке расстояния до 25%.
Кривые блеска типа Ia
Сверхновые типа Ia являются одними из лучших способов определения внегалактических расстояний. Ia происходит, когда двойной белый карлик начинает аккрецировать материю от своей звезды-компаньона. Когда белый карлик набирает материю, в конце концов, он достигает своего Предел Чандрасекара из .
Достигнув ее, звезда становится нестабильной и подвергается безудержной реакции ядерного синтеза. Поскольку все сверхновые типа Ia взрываются примерно с одинаковой массой, их абсолютные величины одинаковы. Это делает их очень полезными в качестве стандартных свечей. Все сверхновые типа Ia имеют стандартный синий цвет и визуальную величину
Следовательно, при наблюдении сверхновой типа Ia, если можно определить ее пиковую величину, можно рассчитать расстояние до нее. По сути, нет необходимости фиксировать сверхновую непосредственно при ее максимальной величине; с использованием многоцветная форма кривой блеска метод (MLCS) форма кривой блеска (полученная в любое разумное время после начального взрыва) сравнивается с семейством параметризованных кривых, которые определяют абсолютную звездную величину при максимальной яркости. Этот метод также учитывает межзвездное поглощение / затемнение от пыли и газа.
Точно так же метод растяжения соответствует определенной кривой блеска сверхновой звезды к шаблонной кривой блеска. Этот шаблон, в отличие от нескольких кривых блеска на разных длинах волн (MLCS), представляет собой просто одну кривую блеска, растянутую (или сжатую) во времени. Используя это Фактор растяжения, пиковая величина может быть определена.[нужна цитата]
Использование сверхновых типа Ia - один из наиболее точных методов, особенно потому, что взрывы сверхновых могут быть видны на больших расстояниях (их светимость сопоставляется со светимостью галактики, в которой они расположены), намного дальше, чем переменные цефеид (в 500 раз дальше). Много времени было посвящено отработке этого метода. Текущая погрешность приближается к 5%, что соответствует погрешности всего 0,1 величины.
Новинки в определениях расстояний
Novae могут использоваться во многом так же, как сверхновые, для определения внегалактических расстояний. Существует прямая зависимость между максимальной звездной величиной новой звезды и временем, в течение которого ее видимый свет уменьшится на две звездные величины. Показано, что это соотношение:
Где - это производная по времени от звездной величины новой звезды, описывающая среднюю скорость убывания первых двух звездных величин.
После того, как новые звезды исчезают, они примерно такие же яркие, как самые яркие переменные звезды цефеид, поэтому оба этих метода имеют примерно одинаковое максимальное расстояние: ~ 20 Мпк. Погрешность этого метода дает погрешность порядка ± 0,4.
Функция светимости шарового скопления
На основе метода сравнения светимости шаровых скоплений (расположенных в гало галактик) от далеких галактик со светимостью Скопление Девы, то функция светимости шарового скопления несет неопределенность расстояния около 20% (или 0,4 звездной величины).
Американский астроном Уильям Элвин Баум впервые попытался использовать шаровые скопления для измерения далеких эллиптических галактик. Он сравнил самые яркие шаровые скопления в галактике Дева A с скоплениями в Андромеде, предполагая, что светимости скоплений одинаковы в обоих. Зная расстояние до Андромеды, Баум предположил прямую корреляцию и оценил расстояние до Девы А.
Баум использовал только одно шаровое скопление, но отдельные образования часто бывают плохими стандартными свечами. Канадский астроном Рене Расин предположили, что использование функции светимости шарового скопления (GCLF) приведет к лучшему приближению. Количество шаровых скоплений в зависимости от величины определяется выражением:
где м0 величина оборота, M0 - величина скопления Девы, а сигма - дисперсия ~ 1,4 магн.
Важно помнить, что предполагается, что все шаровые скопления имеют примерно одинаковую светимость в пределах вселенная. Не существует универсальной функции светимости шаровых скоплений, применимой ко всем галактикам.
Функция светимости планетарной туманности
Подобно методу GCLF, аналогичный численный анализ может быть использован для планетарные туманности (обратите внимание на использование более одного!) в пределах далеких галактик. В функция светимости планетарной туманности (PNLF) был впервые предложен в конце 1970-х годов Холландом Коулом и Дэвидом Дженнером. Они предположили, что все планетарные туманности могут иметь одинаковую максимальную внутреннюю яркость, которая теперь рассчитана как M = -4,53. Это сделало бы их потенциальными стандартными свечами для определения внегалактических расстояний.
Позже астроном Джордж Ховард Джейкоби и его коллеги предположили, что функция PNLF равна:
Где N (M) - номер планетарной туманности, имеющей абсолютную звездную величину M. M * равен туманности с самой яркой звездной величиной.
Метод флуктуации поверхностной яркости
Следующий метод касается общих свойств, присущих галактикам. Эти методы, хотя и с различным процентом ошибок, могут давать оценки расстояний, превышающих 100 Мпк, хотя обычно они применяются более локально.
В флуктуация поверхностной яркости (SBF) метод использует преимущества использования CCD камеры на телескопы. Из-за пространственных колебаний поверхностной яркости галактики некоторые пиксели на этих камерах улавливают больше звезд, чем другие. Однако по мере увеличения расстояния изображение становится все более плавным. Анализ этого описывает величину изменения от пикселя к пикселю, которая напрямую связана с расстоянием до галактики.
Отношение сигма-D
В Отношение сигма-D (или отношение Σ-D), используемое в эллиптические галактики, связывает угловой диаметр (D) галактики с ее дисперсия скоростей. Чтобы понять этот метод, важно точно описать, что представляет собой D. Это, точнее, угловой диаметр галактики до поверхностная яркость уровень 20,75 B-mag arcsec−2. Эта поверхностная яркость не зависит от реального расстояния галактики от нас. Вместо этого D обратно пропорционален расстоянию до галактики, представленному как d. Таким образом, это отношение не использует стандартные свечи. Скорее, D обеспечивает стандартная линейка. Эта связь между D и Σ есть
Где C - константа, которая зависит от расстояния до скоплений галактик.[нужна цитата]
Этот метод потенциально может стать одним из сильнейших методов вычисления галактических расстояний, возможно, превзойдя диапазон даже метода Талли – Фишера. Однако на сегодняшний день эллиптические галактики недостаточно ярки, чтобы обеспечить калибровку этого метода с помощью таких методов, как цефеиды. Вместо этого калибровка выполняется с использованием более грубых методов.
Перекрытие и масштабирование
Последовательность индикаторов расстояния, которая представляет собой лестницу расстояний, необходима для определения расстояний до других галактик. Причина в том, что объекты, достаточно яркие, чтобы их можно было распознать и измерить на таких расстояниях, настолько редки, что их мало или совсем нет поблизости, поэтому слишком мало примеров достаточно близко с надежным тригонометрическим параллаксом для калибровки индикатора. Например, переменные цефеид, один из лучших индикаторов для близлежащих спиральные галактики, пока нельзя удовлетворительно откалибровать только с помощью параллакса, хотя космическая миссия Gaia теперь может решить эту конкретную проблему. Ситуация усложняется еще и тем, что в разных звездных популяциях, как правило, присутствуют не все типы звезд. В частности, цефеиды - это массивные звезды с коротким временем жизни, поэтому их можно будет найти только в местах, где звезды образовались совсем недавно. Следовательно, поскольку эллиптические галактики обычно уже давно перестали иметь крупномасштабное звездообразование, у них не будет цефеид. Вместо этого следует использовать индикаторы расстояния, происхождение которых связано с более старым звездным населением (например, новые звезды и переменные RR Лиры). Однако переменные RR Лиры менее ярки, чем цефеиды, и новые звезды непредсказуемы, и требуется интенсивная программа мониторинга - и удача в этой программе - чтобы собрать достаточно новых звезд в целевой галактике для хорошей оценки расстояния.
Поскольку более далекие ступени лестницы космических расстояний зависят от ближайших, более далекие ступени включают в себя эффекты ошибки на более близких этапах, как систематических, так и статистических. Результат этих распространение ошибок означает, что расстояния в астрономии редко известны с той же точностью, что и измерения в других науках, и что точность неизбежно хуже для более удаленных типов объектов.
Еще одна проблема, особенно для самых ярких стандартных свечей, - это их «стандартность»: насколько однородны объекты в их истинной абсолютной величине. Для некоторых из этих различных стандартных свечей однородность основана на теориях о формирование и эволюция звезд и галактик, и поэтому также подвержены неопределенностям в этих аспектах. Для наиболее ярких индикаторов расстояния, сверхновых типа Ia, эта однородность, как известно, низкая.[44][требуется разъяснение]; однако никакой другой класс объектов не является достаточно ярким, чтобы быть обнаруженным на таких больших расстояниях, поэтому этот класс полезен просто потому, что реальной альтернативы нет.
Результат наблюдения закона Хаббла, пропорциональный взаимосвязь между расстоянием и скоростью, с которой галактика удаляется от нас (обычно называемая красное смещение) является продуктом космической дистанционной лестницы. Эдвин Хаббл заметил, что более слабые галактики имеют большее красное смещение. Определение значения постоянной Хаббла было результатом десятилетий работы многих астрономов, как по сбору измерений красных смещений галактик, так и по калибровке ступеней лестницы расстояний. Закон Хаббла - это основное средство, которое у нас есть для оценки расстояний до квазары и далекие галактики, в которых нельзя увидеть отдельные индикаторы расстояния.
Смотрите также
Сноски
- ^ Если бы сигнал зависел от отдельных масс по отдельности, в сигнале самого низкого порядка не было бы достаточно наблюдаемой информации, чтобы сделать вывод о его внутренней громкости. Это вырождение между массами имеет решающее значение для измерения громкости, но это не случайно: оно имеет фундаментальное происхождение в безмасштабной природе гравитации в общей теории относительности Эйнштейна.[17]
Рекомендации
- ^ Ash, M.E .; Шапиро, И. И .; Смит, В. Б. (1967). «Астрономические константы и планетарные эфемериды, выведенные из радиолокационных и оптических наблюдений». Астрономический журнал. 72: 338. Bibcode:1967AJ ..... 72..338A. Дои:10.1086/110230.
- ^ Perryman, M.A.C .; и другие. (1999). "Каталог HIPPARCOS". Астрономия и астрофизика. 323: L49 – L52. Bibcode:1997A & A ... 323L..49P.
- ^ Harrington, J.D .; Вильярд, Р. (10 апреля 2014 г.). «Хаббл НАСА продлил звездную ленту в 10 раз дальше в космос». НАСА. Получено 17 октября 2014.
- ^ Riess, A. G .; Casertano, S .; Андерсон, Дж .; MacKenty, J .; Филиппенко, А. В. (2014). "Параллакс за пределами килопарсека от пространственного сканирования широкоугольной камерой 3 на космическом телескопе Хаббла". Астрофизический журнал. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ ... 785..161R. Дои:10.1088 / 0004-637X / 785/2/161. S2CID 55928992.
- ^ Brown, A.G.A .; и другие. (Коллаборация Gaia) (август 2018 г.). "Гайя Выпуск данных 2: сводка содержания и свойств опроса ". Астрономия и астрофизика. 616. A1. arXiv:1804.09365. Bibcode:2018A & A ... 616A ... 1G. Дои:10.1051/0004-6361/201833051.
- ^ Б., Байдьянатх (2003). Введение в астрофизику. PHI Learning Private Limited. ISBN 978-81-203-1121-3.
- ^ «Хаббл обнаружил, что Вселенная расширяется быстрее, чем ожидалось». Получено 3 июн 2016.
- ^ «Хаббл растягивает звездную рулетку в десять раз дальше». ESA / Hubble Images. Получено 12 апреля, 2014.
- ^ Поповски, П .; Гулд, А. (1998). «Математика статистического параллакса и местной шкалы расстояний». arXiv:Astro-ph / 9703140.
- ^ Бартель, Н .; и другие. (1994). «Форма, скорость расширения и расстояние до сверхновой 1993J по РСДБ измерениям». Природа. 368 (6472): 610–613. Bibcode:1994Натура.368..610Б. Дои:10.1038 / 368610a0. S2CID 4316734.
- ^ Ферни, Дж. Д. (декабрь 1969 г.). "Связь периода и светимости: исторический обзор". Публикации Тихоокеанского астрономического общества. 81 (483): 707. Bibcode:1969PASP ... 81..707F. Дои:10.1086/128847. ISSN 0004-6280.
- ^ {{cite web | url = https://www.atnf.csiro.au/outreach/education/senior/astrophysics/photometry_magnitude.html#magndistance | title = Определение расстояния до звезд - модуль расстояния | accessdate = 2020-11-02 | publisher = Австралийский национальный центр телескопа
- ^ «Сверхновая типа Ia». Еженедельная тема. Каглоу. Получено 30 января 2012.
- ^ Linden, S .; Virey, J.-M .; Тилькин, А. (2009). "Извлечение космологических параметров и отклонения от эволюции звездной величины сверхновой типа Ia". Астрономия и астрофизика. 506 (3): 1095–1105. arXiv:0907.4495. Bibcode:2009A & A ... 506.1095L. Дои:10.1051/0004-6361/200912811. S2CID 15178494. (И ссылки там.)
- ^ Катлер, Курт; Фланаган, Эанна Э. (15 марта 1994 г.). «Гравитационные волны от слияния компактных двойных систем: насколько точно можно извлечь параметры двойных систем из спиральной формы волны?». Физический обзор D. 49 (6): 2658–2697. arXiv:gr-qc / 9402014. Bibcode:1994ФРВД..49.2658С. Дои:10.1103 / PhysRevD.49.2658. PMID 10017261. S2CID 5808548.
- ^ а б Holz, Daniel E .; Hughes, Scott A .; Шютц, Бернард Ф. (Декабрь 2018 г.). «Измерение космических расстояний стандартными сиренами». Физика сегодня. 71 (12): 34–40. Bibcode:2018ФТ .... 71л..34Ч. Дои:10.1063 / PT.3.4090. ISSN 0031-9228.
- ^ Нападающий Роберт Л.; Берман, Дэвид (12 июня 1967). «Дальность обнаружения гравитационного излучения для двойных звездных систем». Письма с физическими проверками. 18 (24): 1071–1074. Bibcode:1967ПхРвЛ..18.1071Ф. Дои:10.1103 / PhysRevLett.18.1071. ISSN 0031-9007.
- ^ а б c Шютц, Бернард Ф. (25 сентября 1986 г.). «Определение постоянной Хаббла из наблюдений за гравитационными волнами». Природа. 323 (6086): 310–311. arXiv:1307.2638. Bibcode:1986Натура.323..310S. Дои:10.1038 / 323310a0. HDL:11858 / 00-001M-0000-0013-73C1-2. ISSN 0028-0836. S2CID 4327285.
- ^ Хендри, Мартин; Воан, Грэм (февраль 2007 г.). «Гравитационная астрофизика» (PDF). Астрономия и геофизика. 48 (1): 1.10–1.17. Bibcode:2007A&G .... 48a..10H. CiteSeerX 10.1.1.163.5500. Дои:10.1111 / j.1468-4004.2007.48110.x.
- ^ Ниссанке, Самая; Holz, Daniel E .; Hughes, Scott A .; Далал, Нил; Сиверс, Джонатан Л. (10 декабря 2010 г.). «Изучение коротких гамма-всплесков как стандартных сирен гравитационных волн». Астрофизический журнал. 725 (1): 496–514. arXiv:0904.1017. Bibcode:2010ApJ ... 725..496N. Дои:10.1088 / 0004-637X / 725/1/496. HDL:1721.1/60956. ISSN 0004-637X. S2CID 14028891.
- ^ Abbott, B.P .; и другие. (LIGO Scientific Collaboration & Дева Сотрудничество) (16 октября 2017 г.). "Измерение постоянной Хаббла с помощью стандартной сирены с помощью гравитационных волн". Природа. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Натура 551 ... 85А. Дои:10.1038 / природа24471. PMID 29094696.
- ^ Marinoni, C .; и другие. (2008). «Геометрические испытания космологических моделей. I. Исследование темной энергии с использованием кинематики галактик с большим красным смещением». Астрономия и астрофизика. 478 (1): 43–55. arXiv:0710.0759. Bibcode:2008 A&A ... 478 ... 43M. Дои:10.1051/0004-6361:20077116.
- ^ «Световое эхо шепчет расстояние до звезды» (Пресс-релиз). Европейская южная обсерватория. 11 февраля 2008 г.. Получено 2015-10-18.
- ^ Кервелла, Пьер; Меран, Антуан; Сабадош, Ласло; Фуке, Паскаль; Берсер, Дэвид; Помпеи, Эмануэла; Перрин, Гай (2 марта 2008 г.). "Долгопериодическая галактическая цефеида RS Puppis I. Геометрическое расстояние от ее светового эха". Астрономия и астрофизика. 480 (1): 167–178. arXiv:0802.1501. Bibcode:2008 A&A ... 480..167K. Дои:10.1051/0004-6361:20078961.
мы получаем геометрическое расстояние 1992±28 шт. в RS Pup
- ^ Bond, Howard E .; Спаркс, Уильям Б. (4 марта 2009 г.). «Об определении геометрического расстояния до цефеиды RS Puppis по световым отголоскам». Астрономия и астрофизика. 495 (2): 371–377. arXiv:0811.2943. Bibcode:2009A & A ... 495..371B. Дои:10.1051/0004-6361:200810280.
Мы пришли к выводу, что большинство узлов на самом деле, вероятно, лежат перед плоскостью неба, что делает недействительными Кервелла и др. результат. [...] Хотя Kervella et al. результат о расстоянии недействителен, мы показываем, что поляриметрические изображения с высоким разрешением могут дать правильное геометрическое расстояние до этой важной цефеиды.
- ^ Кервелла, Пьер; Bond, Howard E .; Крафт, Мисти; Сабадош, Ласло; Брайтфельдер, Джоанна; Меранд2, Антуан; Спаркс, Уильям Б.; Галленн, Александр; Берсер, Дэвид; Фуке, Паскаль; Андерсон, Ричард И. (декабрь 2014 г.). "Долгопериодическая галактическая цефеида RS Puppis. III. Геометрическое расстояние от поляриметрического изображения HST ее световых эхо". Астрономия и астрофизика. 572: A7 (13 стр.). arXiv:1408.1697. Bibcode:2014A & A ... 572A ... 7K. Дои:10.1051/0004-6361/201424395.
Получаем расстояние 1910±80 шт. (4.2%)
- ^ Бонанос, А. З. (2006). «Затменные двойные системы: инструменты для калибровки шкалы внегалактических расстояний». Материалы симпозиума МАС. 240: 79–87. arXiv:astro-ph / 0610923. Bibcode:2007IAUS..240 ... 79B. CiteSeerX 10.1.1.254.2692. Дои:10.1017 / S1743921307003845. S2CID 18827791.
- ^ Феррарезе, L; и другие. (2000). «База данных модулей расстояния цефеид и кончика ветви красного гиганта, функция светимости шарового скопления, функция светимости планетарной туманности и данные о флуктуации яркости поверхности, полезные для определения расстояния». Серия дополнений к астрофизическому журналу. 128 (2): 431–459. arXiv:Astro-ph / 9910501. Bibcode:2000ApJS..128..431F. Дои:10.1086/313391.
- ^ Колгейт, С. А. (1979). «Сверхновые как стандартная свеча для космологии». Астрофизический журнал. 232 (1): 404–408. Bibcode:1979ApJ ... 232..404C. Дои:10.1086/157300.
- ^ Адаптирован из Джордж Х. Джейкоби; Дэвид Бранч; Робин Чиардулло; Роджер Л. Дэвис; Уильям Э. Харрис; Майкл Дж. Пирс; Кристофер Дж. Притчет; Джон Л. Тонри; Дуглас Л. Велч (1992). «Критический обзор избранных методов измерения внегалактических расстояний». Публикации Тихоокеанского астрономического общества. 104 (678): 599–662. Bibcode:1992PASP..104..599J. Дои:10.1086/133035. JSTOR 40679907.
- ^ Бенедикт, Г. Фриц и др. "Параллаксы сенсора точного наведения космического телескопа Хаббла переменных звезд галактических цефеид: отношения период-светимость", Астрономический журнал, Том 133, выпуск 4, стр. 1810–1827 (2007)
- ^ Majaess, Даниэль; Тернер, Дэвид; Мони Бидин, Кристиан; Мауро, Франческо; Гейслер, Дуглас; Гирен, Вольфганг; Миннити, Данте; Шене, Андре-Николя; Лукас, Филипп; Борисова, Юра; Куртев, Радостн; Декань, Иштван; Сайто, Роберто К. «Новые доказательства в поддержку членства в TW Nor в Lyngå 6 и Centaurus Spiral Arm», Письма ApJ, Volume 741, Issue 2, article id. L2 (2011)
- ^ Stanek, K. Z .; Удальский, А. (1999). «Эксперимент по оптическому гравитационному линзированию. Исследование влияния слияния на шкалу расстояний между цефеидами и цефеидами в большом Магеллановом облаке». arXiv:Astro-ph / 9909346.
- ^ Удальский, А.; Wyrzykowski, L .; Pietrzynski, G .; Szewczyk, O .; Шиманский, М .; Кубяк, М .; Сошинский, И .; Зебрун, К. (2001). «Эксперимент по оптическому гравитационному линзированию. Цефеиды в галактике IC1613: отсутствие зависимости зависимости периода от светимости от металличности». Acta Astronomica. 51: 221. arXiv:astro-ph / 0109446. Bibcode:2001AcA .... 51..221U.
- ^ Ngeow, C .; Канбур, С. М. (2006). "Константа Хаббла от сверхновых звезд типа Ia, калиброванная с помощью линейных и нелинейных соотношений период-светимость цефеид". Астрофизический журнал. 642 (1): L29. arXiv:astro-ph / 0603643. Bibcode:2006ApJ ... 642L..29N. Дои:10.1086/504478. S2CID 17860528.
- ^ Macri, L.M .; Stanek, K. Z .; Bersier, D .; Гринхилл, Л. Дж .; Рид, М. Дж. (2006). «Новое расстояние цефеид до галактики мазер-хозяин NGC 4258 и его значение для постоянной Хаббла». Астрофизический журнал. 652 (2): 1133–1149. arXiv:astro-ph / 0608211. Bibcode:2006ApJ ... 652.1133M. Дои:10.1086/508530. S2CID 15728812.
- ^ Bono, G .; Caputo, F .; Fiorentino, G .; Маркони, М .; Муселла, И. (2008). "Цефеиды во внешних галактиках. I. Мазерная галактика NGC 4258 и зависимость от металличности период-светимость и период-Везенхейт". Астрофизический журнал. 684 (1): 102. arXiv:0805.1592. Bibcode:2008ApJ ... 684..102B. Дои:10.1086/589965. S2CID 6275274.
- ^ Majaess, D .; Тернер, Д .; Лейн, Д. (2009). «Цефеиды типа II как внегалактические дальнобойные свечи». Acta Astronomica. 59 (4): 403. arXiv:0909.0181. Bibcode:2009AcA .... 59..403M.
- ^ Мадор, Барри Ф .; Фридман, Венди Л. (2009). «О наклоне зависимости периода цефеид от светимости». Астрофизический журнал. 696 (2): 1498–1501. arXiv:0902.3747. Bibcode:2009ApJ ... 696.1498M. Дои:10.1088 / 0004-637X / 696/2/1498. S2CID 16325249.
- ^ Scowcroft, V .; Bersier, D .; Mold, J. R .; Вуд, П. Р. (2009). «Влияние металличности на звездные величины цефеид и расстояние до M33». Ежемесячные уведомления Королевского астрономического общества. 396 (3): 43–47. arXiv:0903.4088. Bibcode:2009МНРАС.396.1287С. Дои:10.1111 / j.1365-2966.2009.14822.x.
- ^ Majaess, Д. (2010). «Цефеиды Центавра A (NGC 5128) и последствия для H0». Acta Astronomica. 60 (2): 121. arXiv:1006.2458. Bibcode:2010AcA .... 60..121M.
- ^ Тамманн, Г. А .; Sandage, A .; Рейндл, Б. (2008). «Поле расширения: значение H 0». Ежегодный обзор астрономии и астрофизики. 15 (4): 289. arXiv:0806.3018. Bibcode:2008A и ARv..15..289T. Дои:10.1007 / s00159-008-0012-у. S2CID 18463474.
- ^ Фридман, Венди Л .; Мадор, Барри Ф. (2010). «Постоянная Хаббла». Ежегодный обзор астрономии и астрофизики. 48: 673–710. arXiv:1004.1856. Bibcode:2010ARA & A..48..673F. Дои:10.1146 / annurev-astro-082708-101829. S2CID 119263173.
- ^ Гильфанов, Марат; Богдан, Акос (2010). «Верхний предел вклада аккрецирующих белых карликов в частоту сверхновых типа Ia». Природа. 463 (3): 924–925. arXiv:1002.3359. Bibcode:2010Натура.463..924G. Дои:10.1038 / природа08685. PMID 20164924. S2CID 4389201.
Библиография
- Кэрролл, Брэдли У .; Остли, Дейл А. (2014). Введение в современную астрофизику. Харлоу, Великобритания: Pearson Education Limited. ISBN 978-1-292-02293-2.
- Измерение Вселенной по космологической лестнице расстояний, Стивен Уэбб, авторское право 2001.
- Пасачофф, Дж.; Филиппенко, А. (2013). Космос: астрономия в новом тысячелетии (4-е изд.). Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-68756-1.
- Астрофизический журнал, Функция светимости шарового скопления как индикатор расстояния: динамические эффекты, Острикер и Гнедин, 5 мая 1997 г.
- Введение в измерение расстояний в астрономии, Ричард де Грайс, Чичестер: John Wiley & Sons, 2011 г., ISBN 978-0-470-51180-0.
























