WikiDer > Перекрещенный пентаграммический купол
| Перекрещенный пентаграмматический купол | |
|---|---|
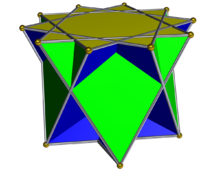 | |
| Тип | Джонсон изоморф Купол |
| Лица | 5 треугольники 5 квадраты 1 пентаграмма 1 декаграмма |
| Края | 25 |
| Вершины | 15 |
| Конфигурация вершины | 5+5(3.4.10/3) 5(3.4.5/3.4) |
| Символ Шлефли | {5/3} || т {5/3} |
| Группа симметрии | C5в, [5], (*55) |
| Группа вращения | C5, [5]+, (55) |
| Двойной многогранник | - |
В геометрия, то скрещенный пентаграмматический купол один из невыпуклых Джонсон солид изоморфы, будучи топологически идентичными выпуклым пятиугольный купол. Его можно получить как кусочек большой ромбоикосододекаэдр или квазиромбикосододекаэдр. Как и во всех купола, база многоугольник вдвое больше края и вершины как верхний; в этом случае базовый многоугольник декаграмма.
Его можно рассматривать как купол с ретроградным пентаграммическим основанием, так что квадраты и треугольники соединяются через основания в противоположном направлении от основания. пентаграмматический куплоид, следовательно, более глубоко пересекаются друг с другом.
Связанные многогранники
| п / d | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  {4/3} |  {5/3} |  {7/3} |  {8/3} |
| 5 | — | — |  {7/5} |  {8/5} |
Перекрещенный пятиугольный купол можно рассматривать как часть однородных многогранников, известных как невыпуклый большой ромбоикосододекаэдр, большой додецикосододекаэдр, и большой ромбидодекаэдр.
 Перекрещенный пентаграммический купол |  Невыпуклый большой ромбоикосододекаэдр |  Большой додецикосододекаэдр |  Большой ромбидодекаэдр |
Различные скрещенные пентаграммы купола на невыпуклом большом ромбикосододекаэдре могут быть уменьшены или повернуты (повернуты), чтобы получить набор из 12 многогранников, изоморфных многограннику. Твердые тела Джонсона J72 к J83. Это круговые, метабигиратные, парабигиратные, тригиратные, уменьшенные, метабидиманишированные, парабидимулированные, трехдисковые, метагиратные уменьшенные, парагиратные уменьшенные, бигиратные уменьшенные и спиральные двунаправленные квазиромбикосидодекаэдры.
Двойной многогранник
Двойник скрещенного пятиугольного купола имеет 10 треугольных и 5 воздушных змеев:
Рекомендации
- Джим Макнил, Связь куполов с однородными многогранниками.
- Джим Макнил, Купол ИЛИ Семикупола
- Ричард Клитцинг, Осесимметричные грани равномерных многогранников.
