WikiDer > Дискретная глобальная сетка
Эта документация требует внимания эксперта в области технологий. Конкретная проблема: Обзор английского языка и необходимость сокращения или обобщения некоторых частей. (Сентябрь 2018 г.) |
| Геодезия | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||||||||||||||||
Концепции
| ||||||||||||||||||||||||||
Стандарты (история)
| ||||||||||||||||||||||||||
А Дискретная глобальная сеть (DGG) это мозаика покрывающий всю поверхность Земли. Математически это разделение пространства: он состоит из набора непустых областей, которые образуют раздел поверхности Земли.[1] В обычной стратегии моделирования сетки для упрощения расчетов положения каждая область представлена точкой, а сетка абстрагируется как набор точек-регионов. Каждый регион или региональная точка в сетке называется ячейка.
Когда каждая ячейка сетки подвергается рекурсивный разбиение, в результате чего получается «серия дискретных глобальных сеток с все более высоким разрешением»,[2] образуя иерархическую сетку, она называется Иерархический DGG (иногда «система ДГГ»).
Дискретные глобальные сетки используются в качестве геометрической основы для построения геопространственных структуры данных. Каждая ячейка связанных с объекты данных или значения, или (в иерархическом случае) могут быть связаны с другими ячейками. DGG были предложены для использования в широком спектре геопространственных приложений, включая векторное и растровое представление местоположения, слияние данных и пространственные базы данных.[1]
Самые обычные сетки для представление горизонтального положения, используя стандартный датум, любить WGS84. В этом контексте также часто используется конкретный DGG в качестве основы для стандартизация геокодирования.
В контексте пространственный индекс, DGG может назначать уникальные идентификаторы каждой ячейке сетки, используя ее для целей пространственной индексации, в базы геоданных или для геокодирование.
Эталонная модель земного шара
«Глобус» в концепции DGG не имеет строгой семантики, но в геодезии так называемый «Ссылка на сетку Система "- это сетка, которая разделяет пространство с точными позициями относительно датум, то есть приближенная "стандартная модель Геоид". Итак, в роли геоида" глобус ", покрываемый DGG, может быть любым из следующих объектов:
- В топографическая поверхность земли, когда каждая ячейка сетки имеет координаты положения на поверхности и высоту по отношению к стандартный геоид. Пример: сетка с координатами (φ, λ, z) где z - высота.
- А стандарт Поверхность геоида. Координата z равна нулю для всей сетки, поэтому может быть опущена, (φ, λ).
В древних стандартах до 1687 г. (публикация «Принципов Ньютона») использовалась «эталонная сфера»; в настоящее время геоид математически абстрагируется как опорный эллипсоид.- А упрощенный геоид: иногда старый геодезический стандарт (например, SAD69) или негеодезическую поверхность (например, идеально сферическую поверхность), и она будет покрыта сеткой. В этом случае ячейки необходимо пометить однозначно, (ф ', λ'), а преобразование (φ, λ) ⟾ (φ ', λ') должно быть известно.
- А проекционная поверхность. Обычно географические координаты (φ, λ) проектируются (с некоторым искажением) на плоскость двухмерного отображения с двумерными декартовыми координатами (х, у).
В качестве глобального процесса моделирования современные DGG, включая процесс проецирования, стремятся избегать поверхностей, таких как цилиндры или конические тела, которые приводят к неоднородностям и проблемам с индексированием. Правильные многогранники и другие топологические эквиваленты сферы привели к наиболее многообещающим известным вариантам, которые должны быть охвачены DGG,[1] потому что "сферические выступы сохраняют правильная топология Земли - нет сингулярностей или разрывов, с которыми нужно было бы иметь дело ".[3]
При работе с DGG важно указать, какой из этих вариантов был принят. Итак, характеристика эталонная модель земного шара DGG можно резюмировать следующим образом:
- Восстановленный объект: тип объекта в роли глобуса. Если проекции нет, то объектом, покрываемым сеткой, является геоид, Земля или сфера; else - это класс геометрии поверхности проекции (например, цилиндр, куб или конус).
- Проекция тип: отсутствует (нет проекции) или присутствует. Если он присутствует, его характеристику можно резюмировать с помощью свойство цели проекции (например, равновеликий, конформный и т. д.) и класс корректирующей функции (например, тригонометрический, линейный, квадратичный и т. д.).
ПРИМЕЧАНИЕ: когда DGG покрывает проекционную поверхность, в контексте происхождение данных, метаданные о базовом геоиде также важны - обычно CRS ISO 19111 значение, без путаницы с поверхностью проецирования.
Виды и примеры
Основной отличительной чертой для классификации или сравнения DGG является использование или отсутствие иерархических структур сетки:
- В иерархический В системах ссылок каждая ячейка является «ссылкой на блок» для подмножества ячеек, и идентификаторы ячеек могут выражать эту иерархию в своей логике или структуре нумерации.
- В неиерархический системы отсчета каждая ячейка имеет отдельный идентификатор и представляет фиксированную область пространства. Дискретизация Система широты / долготы это самый популярный и стандартный справочник по конверсиям.
Другими обычными критериями для классификации DGG являются форма плитки и степень детализации (разрешение сетки):
- Равномерность и форма плитки: бывают обычные, полурегулярные или нерегулярная сетка. Как в общем мозаики правильными многоугольниками, можно облицовывать плиткой с правильной гранью (например, настенная плитка может быть прямоугольной, треугольной, шестиугольной и т. д.) или с тем же типом поверхности, но с изменением ее размера или углов, что приводит к полурегулярной форме.
Равномерность формы и регулярность показателей обеспечивают лучшие алгоритмы индексации сетки. Хотя он имеет менее практическое применение, возможны совершенно нерегулярные сетки, такие как Вороной покрытие. - Мелкий или грубый грануляция (размер ячейки): современные DGG параметризуемы по разрешающей способности сетки, поэтому это характеристика последнего экземпляра DGG, но бесполезна для классификации DGG, за исключением случаев, когда тип DGG должен использовать определенное разрешение или иметь предел дискретизации. Сетка «мелкого» гранулирования не имеет ограничений, а «грубая» означает резкое ограничение. Исторически основные ограничения связаны с цифровыми / аналоговыми носителями, сжатием / расширенным представлением сетки в базе данных и ограничениями памяти для хранения сетки. Когда необходима количественная характеристика, может быть принята средняя площадь ячеек сетки или среднее расстояние между центрами ячеек.
Неиерархические сетки
Наиболее распространенный класс дискретных глобальных сеток - это те, которые размещают центральные точки ячеек на меридианах и параллелях долготы / широты или которые используют меридианы и параллели долготы / широты для формирования границ прямоугольных ячеек. Примеры таких сеток, все основанные на широте / долготе:
| UTM зоны: Делит Землю на шестьдесят (полос) зон, каждая из которых представляет собой полосу долготы в шесть градусов. В цифровых носителях удаляется зона перекрытия. Используйте секущую поперечную проекцию Меркатора в каждой зоне. Определите 60 секущих цилиндров, по 1 на зону. В UTM зоны был усилен Справочная система военной сети (MGRS) путем добавления Группы широты. |  | |||
| начало: 1940-е годы | закрытый объект: цилиндр (60 вариантов) | проекция: UTM или латлонг | неправильная плитка: многоугольные полосы | степень детализации: грубый |
| (современный) UTM - Универсальная поперечная проекция Меркатора: Представляет собой дискретизацию непрерывной сетки UTM с своего рода двухуровневой иерархией, где первый уровень (крупнозернистый) соответствует «зонам UTM с диапазонами широт» ( MGRS), используйте те же 60 цилиндров в качестве объектов эталонной проекции. Каждая мелкозернистая ячейка обозначается структурированным идентификатором, состоящим из «обозначения зоны сетки», «идентификатора квадрата 100 000 метров» и «числового местоположения». Разрешение сетки напрямую зависит от количества цифр в координатах, которое также стандартизировано. Например ячейка 17N 630084 4833438 это площадь ~ 10мx10м.PS: этот стандарт использует 60 различных цилиндров для выступов. Существуют также стандарты «Региональная поперечная проекция Меркатора» (RTM или UTM Regional) и «Местная поперечная проекция Меркатора» (LTM или UTM Local) с более конкретными цилиндрами для лучшей подгонки и точности в интересующей точке. |  | |||
| начало: 1950-е годы | закрытый объект: цилиндр (60 вариантов) | проекция: UTM | прямоугольная плитка: равноугловой (конформный) | степень детализации: хорошо |
| ISO 6709: Дискретизирует традиционное представление "координатной сетки" и современные местоположения на основе ячеек с числовыми координатами. Степень детализации фиксируется простым соглашением о числовом представлении, например. г. сетка с шагом в один градус, сетка с 0,01 градусом и т. д., и это приводит к неравномерной площади ячеек по сетке. Форма ячеек прямоугольная, за исключением полюсов, где они треугольные. Числовое представление стандартизировано двумя основными условными обозначениями: градусы (Приложение D) и десятичные числа (Приложение F). Разрешение сетки контролируется количеством цифр (Приложение H). | 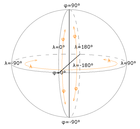 | |||
| начало: 1983 | закрытый объект: Геоид (любой CRS ISO 19111) | проекция: никто | прямоугольная плитка: однородная сфероидальная форма | степень детализации: хорошо |
| Первичный DEM (ОЛОВНАЯ ЦМР): Векторная треугольная нерегулярная сеть (TIN) - набор данных TIN DEM также называется первичной (измеренной) DEM. Многие матрицы высот создаются на сетке точек, размещенных с регулярным угловым приращением широты и долготы. Примеры включают Глобальный набор данных высоты за 30 угловых секунд (GTOPO30).[4] и Глобальные данные о высоте местности с разным разрешением за 2010 г. (GMTED2010).[5] Триангулированная нерегулярная сеть представляет собой представление непрерывной поверхности, целиком состоящей из треугольных граней. |  | |||
| начало: 1970-е годы | закрытый объект: местность | проекция: никто | треугольная неоднородная плитка: параметризованный (векторный) | степень детализации: хорошо |
| Сетки Аракавы: Использовался для моделей системы Земля для метеорология и океанография - например, Глобальная многомасштабная модель окружающей среды (GEM) использует сетки Аракавы для Моделирование глобального климата.[6] Так называемая «A-сетка» - эталонный DGG, для сравнения с другими DGG. Используется в 1980-х годах с пространственным разрешением ~ 500x500. | ||||
| начало: 1977 | закрытый объект: геоид | проекция: ? | прямоугольная плитка: параметрический, пространство-время | степень детализации: Средняя |
| Площади ВМО: Специализированная сетка, уникально используемая NOAA, делит карту мира с линиями сетки широты и долготы на ячейки сетки с широтой 10 ° и долготой 10 °, каждая из которых имеет уникальный 4-значный числовой идентификатор (первая цифра обозначает квадранты NE / SE / SW / NW). | ||||
| начало: 2001 | закрытый объект: геоид | проекция: никто | Обычная плитка: Прямоугольные ячейки 36x18 | степень детализации: грубый |
| Квадраты мировой сетки: Являются совместимым расширением японских квадратов сетки, стандартизованных в промышленных стандартах Японии (JIS X0410), на весь мир. Код World Grid Square может определять квадраты сетки, покрывающие мир, на основе 6 слоев. Мы можем выразить квадрат сетки, используя последовательность от 6 до 13 цифр в соответствии с его разрешением.[7] | ||||
| начало: ? | закрытый объект: геоид | проекция: ? | ? плитка: ? | степень детализации: ? |
Иерархические сетки
На иллюстрации справа показаны 3 карты границ побережья Великобритании. Первая карта была покрыта сеткой уровня 0 с ячейками размером 150 км. Только серая ячейка в центре, без увеличения детализации, остается нулевым уровнем; все остальные ячейки второй карты были разделены на сетку из четырех ячеек (уровень сетки-1), каждая по 75 км. На третьей карте 12 ячеек уровня 1 остаются серыми, все остальные были снова разделены, каждая ячейка уровня 1 преобразована в сетку уровня 2.
Примеры DGG которые используют такой рекурсивный процесс, генерируя иерархические сетки, включают:
| Дискретные глобальные сети ISEA (ISEA DGGs): Представляют собой класс сеток, предложенных исследователями Государственный университет Орегона.[1] Ячейки сетки создаются в виде правильных многоугольников на поверхности икосаэдр, а затем обратная проекция с использованием картографической проекции Икосаэдра Снайдера (ISEA)[8] чтобы сформировать равные по площади ячейки на сфере. Ориентация икосаэдра относительно Земли может быть оптимизирована по различным критериям.[9] Ячейки могут быть шестиугольниками, треугольниками или четырехугольники. Множественные разрешения указываются путем выбора отверстие, или соотношение между областями ячеек при последовательных разрешениях. Некоторые приложения ISEA DGG включают информационные продукты, созданные Европейское космическое агентствос Влага почвы и соленость океана (SMOS) спутник, который использует ISEA4H9 (апертура 4 гексагональной DGGS, разрешение 9),[10] и коммерческое программное обеспечение Global Grid Systems Insight,[11] который использует ISEA3H (апертура 3 гексагональной DGGS). | ||||
| начало: 1992..2004 | закрытый объект: ? | проекция: равновеликий | параметризованные (шестиугольники, треугольники или четырехугольники) плитки: равновеликий | степень детализации: хорошо |
| COBE - четырехугольный сферический куб: Куб:[12] Подобное разложение сферы у HEALPix и S2. Но не использует кривую, заполняющую пространство, ребра не являются геодезическими, а проекция более сложна. | ||||
| начало: 1975..1991 | закрытый объект: куб | проекция: Криволинейная перспектива | четырехугольная плитка: равномерное сохранение площади | степень детализации: хорошо |
| Четвертичная треугольная сетка (QTM): QTM имеет ячейки треугольной формы, образованные 4-кратным рекурсивным делением сферического октаэдра.[13] | ||||
| начало: 1999 ... 2005 | закрытый объект: октаэдр (или другое) | проекция: Цилиндрический равновеликий Ламберта | треугольная плитка: униформа с сохранением площади | степень детализации: хорошо |
| Иерархическая равновеликая пикселизация isoLatitude (HEALPix): {{{2}}} |  | |||
| начало: 2006 | закрытый объект: Геоид | проекция: (K, H) параметризованная проекция HEALPix | плитки qradrilater: униформа с сохранением площади | степень детализации: хорошо |
| Иерархическая треугольная сетка (HTM): HTM, разработанный в 2003 ... 2007 годах, представляет собой многоуровневое рекурсивное разложение сферы. Оно начинается с октаэдра, пусть это будет уровень 0. Когда вы проецируете края октаэдра на (единичную) сферу, создается 8 сферических треугольников: 4 в Северном и 4 в Южном полушариях ".[15] Таким образом, каждый треугольник делится на 4 подтреугольника (разделение от 1 до 4). Первая общедоступная операционная версия кажется[16] HTM-v2 в 2004 году. |  | |||
| начало: 2004 | закрытый объект: Геоид | проекция: никто | треугольная плитка: сферические эквилатеры | степень детализации: хорошо |
| Geohash: Широта и долгота объединяются, вводя биты в объединенное число. Двоичный результат представлен с помощью base32, предлагая компактный, удобочитаемый код. При использовании в качестве пространственный индекс, соответствует Кривая Z-порядка. Есть несколько вариантов вроде Геохаш-36. |  | |||
| начало: 2008 | закрытый объект: Геоид | проекция: никто | полурегулярная плитка: прямоугольный | степень детализации: хорошо |
| S2 / S2 Регион: «Система сеток S2» является частью «Библиотеки геометрии S2»[17] (название происходит от математической записи для n-сфера, S²). Он реализует индексную систему на основе проекция куба и заполнение пространства Кривая Гильберта, разработанная в Google.[18][19] S2Region S2 является наиболее общим представлением его ячеек, где можно вычислить положение ячейки и метрику (например, площадь). Каждый S2Region является подсеткой, в результате чего иерархия ограничивается 31 уровнем. На уровне 30 оценивается разрешение[20] в 1 см², на уровне 0 составляет 85011012 км². Идентификатор ячейки иерархической сетки грани куба (6 граней) имеет идентификатор 60 бит (так что «каждый см² на Земле можно представить с помощью 64-битного целого числа). |  | |||
| начало: 2015 | закрытый объект: куб | проекция: сферические проекции в каждой грани куба с использованием квадратичной функции | полурегулярная плитка: четырехугольные выступы | степень детализации: хорошо |
| S2 / S2LatLng: DGG, предоставляемый представлением S2LatLng, похож на сетку ISO 6709, но иерархический и с определенной формой ячейки. | ||||
| начало: 2015 | закрытый объект: Геоид или сфера | проекция: никто | полурегулярная плитка: четырехугольник | степень детализации: хорошо |
| S2 / S2CellId: DGG предоставляется представлением S2CellId. Каждый идентификатор ячейки представляет собой уникальный 64-битовый целочисленный идентификатор без знака для любого уровня иерархии. | ||||
| начало: 2015 | закрытый объект: куб | проекция: ? | полурегулярная плитка: четырехугольник | степень детализации: хорошо |
Стандартные равновеликие иерархические сетки
Существует класс иерархических DGG, названный Открытый геопространственный консорциум (OGC) как «Дискретные глобальные сетевые системы» (DGGS), который должен удовлетворять 18 требованиям. Среди них то, что лучше всего отличает этот класс от других иерархических групп DGG, - это Требование-8, «Для каждого последующего уровня уточнения сетки и для каждой геометрии ячеек (...) Ячейки равной площади (...) в пределах указанного уровня точности».[21]
DGGS разработан как основа для информации в отличие от обычных системы координат изначально предназначен для навигации. Для того чтобы глобальная пространственная информационная структура на основе сетки могла эффективно работать в качестве аналитической системы, она должна быть построена с использованием ячеек, которые равномерно представляют поверхность Земли.[21] Стандарт DGGS включает в свои требования набор функций и операций, которые должна предлагать структура.
Все ячейки DGGS уровня 0 представляют собой грани равной площади. Правильные многогранники...
Моделирование базы данных

Есть много DGG, потому что есть много альтернативных представлений, оптимизации и моделирования. Вся сетка DGG представляет собой композицию своих ячеек, и в иерархической DGG каждая ячейка использует новую сетку над своим локальным регионом.
Иллюстрация не подходит ОЛОВНАЯ ЦМР случаи и аналогичные структуры «необработанных данных», где в базе данных используется не концепция ячеек (которая геометрически представляет собой треугольная область), а узлы и ребра: каждый узел - это отметка, а каждое ребро - это расстояние между двумя узлами.
В общем, каждая ячейка DGG идентифицируется координатами своей региональной точки (показанной как центральная точка представления базы данных). Также возможно, с потерей функциональности, использовать «свободный идентификатор», то есть любой уникальный номер или уникальную символическую метку для каждой ячейки, идентификатор ячейки. ID обычно используется как пространственный индекс (например, внутренний Quadtree или k-d дерево), но также возможно преобразовать идентификатор в понятную человеку этикетку для геокодирование Приложения.
Современные базы данных (например, использующие сетку S2) также используют несколько представлений для одних и тех же данных, предлагая как сетку (или область ячеек) на основе геоида, так и сетку на основе проекции.
Структура DGGS
Стандарт определяет требования иерархической DGG, в том числе о том, как управлять сетью. Любой DGG, который удовлетворяет этим требованиям, можно назвать DGGS. «Спецификация DGGS ДОЛЖНА включать опорную рамку DGGS и связанные с ней функциональные алгоритмы, как определено в базовой концептуальной модели данных DGGS».[22]
- Чтобы система сетки Земли соответствовала этой абстрактной спецификации, она должна определять иерархическую тесселяцию ячеек равной площади, которые разделяют всю Землю на несколько уровней детализации и обеспечивают глобальную пространственную систему отсчета. Система также должна включать методы кодирования для: адресации каждой ячейки; назначать квантованные данные ячейкам; и выполнять алгебраические операции с ячейками и назначенными им данными. Основные концепции базовой концептуальной модели данных DGGS:
- элементы системы отсчета, и,
- элементы функционального алгоритма; в составе:
- операции квантования,
- алгебраические операции и
- операции взаимодействия.
История
Дискретные глобальные сети с областями ячеек, определяемыми параллелями и меридианами широта/долгота использовались с первых дней мировой геопространственные вычисления. До этого дискретизация непрерывных координат для практических целей с помощью бумажных карт происходила только с низкой степенью детализации. Возможно, наиболее представительным и главным примером DGG этой доцифровой эпохи были военные UTM DGG, с более мелкой гранулированной идентификацией клеток для геокодирование целей. Подобным образом некоторые иерархическая сетка существует до геопространственных вычислений, но только в грубой грануляции.
Глобальная поверхность не требуется для использования на ежедневных географических картах, а до 2000-х годов память была очень обширной, чтобы помещать все планетарные данные в один и тот же компьютер. Первые цифровые глобальные сетки использовались для обработки данных спутниковых изображений и глобальных (климатический и океанографический) моделирование гидродинамики.
Первые опубликованные ссылки на Иерархическая геодезическая ГДГ системы относятся к системам, разработанным для моделирования атмосферы и опубликованным в 1968 году. Эти системы имеют области гексагональных ячеек, созданные на поверхности сферической икосаэдр.[23][24]
Пространственные иерархические сетки стали предметом более интенсивных исследований в 1980-х гг.[25] когда основные конструкции, как Quadtree, были адаптированы для индексации изображений и баз данных.
Хотя конкретные экземпляры этих сеток использовались десятилетиями, термин Дискретные глобальные сети были придуманы исследователями в Государственный университет Орегона в 1997 г.[2] чтобы описать класс всех таких сущностей.
... Стандартизация OGC в 2017 году ...
Сравнение и эволюция
Оценка дискретной глобальной сети состоит из множества аспектов, включая площадь, форму, компактность и т. Д. Методы оценки для картографическая проекция, такие как Индикатриса Тиссо, также подходят для оценки дискретной глобальной сетки на основе картографической проекции.

Кроме того, усредненное соотношение дополнительных профилей (AveRaComp) [26] дает хорошую оценку искажений формы для четырехугольной дискретной глобальной сетки.
Варианты разработки и адаптации баз данных ориентированы на практические требования к большей производительности, надежности и точности. Выбираются лучшие варианты, которые адаптируются к потребностям, способствуя эволюции архитектур DGG. Примеры этого процесса эволюции: от неиерархических к иерархическим DGG; от использования индексов Z-кривой (a наивный алгоритм на основе чередования цифр), используемых Geohash, в индексы кривой Гильберта, используемые в современных оптимизациях, таких как S2.
Варианты геокодирования
Как правило, каждая ячейка сетки идентифицируется координатами своей точки региона, но также можно упростить синтаксис и семантику координат, чтобы получить идентификатор, как в классическом буквенно-цифровые сетки - и найдите координаты региональной точки по ее идентификатору. Небольшие и быстрые представления координат - цель реализаций идентификаторов сот для любых решений DGG.
Нет потери функциональности при использовании «свободного идентификатора» вместо координаты, то есть любого уникального номера (или уникальной символической метки) для каждой точки региона, идентификатор ячейки. Таким образом, преобразование координаты в удобочитаемую метку и / или сжатие длины метки является дополнительным шагом в представлении сетки. Это представление называется геокодировать.
Некоторые популярные "глобальные коды мест" так как ISO 3166-1 альфа-2 для административных районов или Код Лонгхерста для экологических регионов земного шара, являются частичный в глобальном охвате. С другой стороны, любой набор идентификаторов ячеек определенного DGG может использоваться как "полный охват коды мест ». Каждый набор идентификаторов, используемый в качестве стандарта для обмена данными, называется« системой геокодирования ».
Есть много способов представить значение идентификатора ячейки (идентификатор ячейки) сетки: структурированная или монолитная, двоичная или нет, читаемая человеком или нет. Предположим, что функция карты, например Фонтан Мерлион в Сингапуре (Масштаб ~ 5 м), представленный его минимальная ограничивающая ячейка или ячейка с центральной точкой, идентификатор ячейки будет:
| ID соты | Название и параметры варианта DGG | Структура ID; разрешение сетки |
|---|---|---|
| (1 ° 17 ′ 13,28 ″ с.ш., 103 ° 51 ′ 16,88 ″ в.д.) | ISO 6709 / D в градусах (приложение), CRS = WGS84 | широта(град мин сек директ) длинная(град мин сек директ); секунды с 2-мя дробными местами |
| (1.286795, 103.854511) | ISO 6709 / F в десятичном формате и CRS = WGS84 | (широта, долгота); 6 фракционных мест |
| (1.65AJ, 2V.IBCF) | ISO 6709 / F в десятичном формате с основанием 36 (не ISO) и CRS = WGS84 | (широта, долгота); 4 фракционных места |
| w21z76281 | Geohash, base32, WGS84 | монолитный; 9 символов |
| 6PH57VP3 + PR | PlusCode, base20, WGS84 | монолитный; 10 символов |
| 48N 372579 142283 | UTM, стандартное десятичное число, WGS84 | зона широта долгая; 3 + 6 + 6 цифр |
| 48Н 7ЖФ 31СБ | UTM, база координат36, WGS84 | зона широта долгая; 3 + 4 + 4 цифры |
Все эти геокоды представляют одно и то же положение на земном шаре с одинаковой точностью, но отличаются строка-длина, использование разделителей и алфавит (символы без разделителей). В некоторых случаях может использоваться "исходное представление DGG". Варианты представляют собой незначительные изменения, затрагивающие только окончательное представление, например основу числового представления, или чередование частей структурированного только в одно числовое или кодовое представление. Наиболее популярные варианты используются для приложений геокодирования.
Алфавитно-цифровые глобальные сетки
DGG и его варианты, с человек читаемый идентификаторы ячеек, использовались как де-факто стандарт для буквенно-цифровые сетки. Он не ограничивается буквенно-цифровыми символами, но «буквенно-цифровой» является наиболее распространенным термином.
Геокоды - это обозначения для местоположений, а в контексте DGG - обозначения для выражения идентификаторов ячеек сетки. Цифровые стандарты и группы DGG постоянно развиваются, поэтому в последние годы популярность каждого соглашения о геокодировании постоянно меняется. Более широкое внедрение также зависит от принятия правительством страны, использования в популярных картографических платформах и многих других факторов.
Примеры, используемые в следующем списке, относятся к "второстепенной ячейке сетки", содержащей Вашингтонский обелиск, 38 ° 53 ′ 22,11 ″ с.ш., 77 ° 2 ′ 6,88 ″ з.д..
| DGG имя / var | Начало и лицензия | Краткое изложение варианта | Описание и пример |
|---|---|---|---|
| Зоны UTM / без перекрытия | 1940-е годы - CC0 | оригинал без наложений | Делит Землю на шестьдесят многоугольных полос. Пример: 18S |
| Дискретный UTM | 1940-е годы - CC0 | оригинал Целые числа UTM | Делит Землю на шестьдесят зон, каждая из которых представляет собой полосу долготы в шесть градусов, и использует секущую поперечную проекцию Меркатора в каждой зоне. Нет информации о первом цифровом использовании и соглашениях. Предположили, что стандартизация была позже ISO (1980-е). Пример: 18S 323483 4306480 |
| ISO 6709 | 1983 - CC0 | оригинал представительство степени | Разрешение сетки зависит от количества цифр - при необходимости заполняются начальные нули, а дробная часть - с соответствующим количеством цифр для представления требуемой точности сетки. Пример: 38 ° 53 ′ 22,11 ″ с.ш., 77 ° 2 ′ 6,88 ″ з.д.. |
| ISO 6709 | 1983 - CC0 | Представление 7 десятичных цифр | Вариант основан на представлении XML, где структура данных является "кортеж, состоящий из широты и долготы, представляет двухмерное географическое положение", и каждое число в кортеже представляет собой действительное число с семью десятичными знаками. Пример: 38.889475, -77.035244. |
| Mapcode | 2001 - запатентовано | оригинал | Первый, кто принял код смеси в сочетании с кодами ISO 3166 (страна или город). В 2001 году алгоритмы были лицензированы Apache2, но вся система осталась запатентованной. |
| Geohash | 2008 - CC0 | оригинал | Похож на latLong с битовой развёрткой, а результат представлен как base20. |
| Геохаш-36 | 2011 - CC0 | оригинал | Несмотря на похожее название, не использует тот же алгоритм, что и Geohash. Использует сетку 6 на 6 и связывает буквы с каждой ячейкой. |
| What3words | 2013 запатентовано | оригинал (Английский) | конвертирует квадраты 3x3 метра в 3 слова из английского словаря.[27] |
| PlusCode | 2014 - Apache2[28] | оригинал | Также называется «Открытый код местоположения». Коды представляют собой числа в формате base20 и могут использовать названия городов, уменьшая код на размер города. Ограничительная рамка код (например, стратегия Mapcode). Пример: 87C4VXQ7 + QV. |
| S2 Идентификатор соты / Base32 | 2015 - Apache2[29] | оригинал 64-битное целое число, выраженное как base32 | Иерархическая и очень эффективная индексация базы данных, но нет стандартного представления для base32 и префиксов городов, как PlusCode. |
| What3words/ otherLang | 2016 ... 2017 - запатентовано | Другие языки | То же, что и английский, но с использованием другого словаря в качестве справочника для слов. Португальский пример и ячейка 10x14 м: tenaz.fatual.davam. |
Другие задокументированные варианты, но предполагается, что они не используются или «никогда не будут популярными»:
| Имя DGG | Начало - лицензия | Резюме | Описание |
|---|---|---|---|
| C-квадраты | 2003 - «Без ограничений» | Latlong чересстрочный | Десятичное чередование представлений ISO LatLong в градусах. Это «наивный» алгоритм по сравнению с двоичным чередованием или Geohash. |
| ГЕОРЕФ | ~ 1990 - CC0 | На основе стандарта ISO LatLong, но используются более простые и лаконичные обозначения. | «Мировая географическая справочная система», военная / аэронавигационная система координат для определения точек и территорий. |
| Geotude | ? | ? | ? |
| ГАРС | 2007 - ограничено | США / NGA | Справочная система разработана Национальным агентством геопространственной разведки (NGA). "стандартизированная система отсчета области боевого пространства в Министерстве обороны, которая повлияет на весь спектр разрешения конфликтов в боевом пространстве" |
| Площади ВМО | 2001 .. - CC0? | специализированный | Ячейки загрузки изображений NOAA. ... делит карту мира с линиями сетки широты и долготы на ячейки сетки 10 ° широты на 10 ° долготы, каждая из которых имеет уникальный 4-значный числовой идентификатор. Прямоугольные ячейки размером 36x18 (обозначены четырьмя цифрами, первая цифра обозначает квадранты NE / SE / SW / NW). |
Смотрите также
использованная литература
- ^ а б c d Сахр, Кевин; Белый, Денис; Кимерлинг, А.Дж. (2003). «Геодезические дискретные глобальные сеточные системы» (PDF). Картография и географическая информатика. 30 (2): 121–134. Дои:10.1559/152304003100011090.
- ^ а б Сахр, Кевин; Белый, Денис; Кимерлинг, А.Дж. (18 марта 1997 г.), «Предлагаемые критерии для оценки дискретных глобальных сетей», Проект технического отчета, Корваллис, Орегон: Университет штата Орегон
- ^ "Обзор".
- ^ "Глобальное превышение 30 угловых секунд (GTOPO30)". USGS. Архивировано из оригинал 10 июля 2017 г.. Получено 8 октября, 2015.
- ^ «Глобальные данные о высоте местности с разным разрешением за 2010 г. (GMTED2010)». USGS. Получено 8 октября, 2015.
- ^ Аракава, А .; Лэмб, В. (1977). «Расчетное моделирование основных динамических процессов модели общей циркуляции UCLA». Методы вычислительной физики. 17. Нью-Йорк: Academic Press. С. 173–265.
- ^ «Научно-исследовательский институт мировых сеточных квадратов». Йокогамский городской университет. Получено Двадцать первое ноября, 2017.
- ^ Снайдер, Дж. П. (1992). «Плоская проекция многогранных глобусов». Картографика. 29 (1): 10–21. Дои:10.3138 / 27х7-8к88-4882-1752.
- ^ Барнс, Ричард (2019). «Оптимальные ориентации дискретных глобальных сеток и полюса недоступности». Международный журнал Digital Earth. Дои:10.1080/17538947.2019.1576786.
- ^ Suess, M .; Matos, P .; Gutierrez, A .; Zundo, M .; Мартин-Нейра, М. (2004). «Обработка данных SMOS уровня 1с на дискретную глобальную сетку». Материалы Международного симпозиума IEEE по наукам о Земле и дистанционному зондированию: 1914–1917.
- ^ "Global Grid Systems Insight". Глобальные сетевые системы. Получено 8 октября, 2015.
- ^ "LAMBDA - COBE Четырехсторонний сферический куб".
- ^ Даттон, Г. (1999). Иерархическая система координат для геообработки и картографии. Springer-Verlag.
- ^ «Фоновая цель HEALPix». Лаборатория реактивного движения НАСА. Получено 8 октября, 2015.
- ^ «Обзор HTM».
- ^ "Материалы конференции ADASS 2003".
- ^ "S2 Геометрия".
- ^ "Обзор". s2geometry.io. Получено 2018-05-11.
- ^ Крейсс, Свен (27.07.2016). «Ячейки S2 и кривые заполнения пространства: ключи к созданию лучших инструментов цифровой карты для городов». Средняя. Получено 2018-05-11.
- ^ «Статистика ячейки S2».
- ^ а б Открытый геопространственный консорциум (2017), «Тема 21: Абстрактная спецификация дискретных глобальных грид-систем». Документ 15-104r5 версия 1.0.
- ^ Раздел 6.1 «Обзор базовой модели данных DGGS» стандарта DGGS
- ^ Sadourny, R .; Аракава, А .; Минц, Ю. (1968). «Интегрирование недивергентного уравнения баротропной завихренности с икосаэдрально-гексагональной сеткой для сферы». Ежемесячный обзор погоды. 96 (6): 351–356. CiteSeerX 10.1.1.395.2717. Дои:10.1175 / 1520-0493 (1968) 096 <0351: iotnbv> 2.0.co; 2.
- ^ Уильямсон, Д. (1968). «Интегрирование уравнения баротропной завихренности на сферической геодезической сетке». Скажи нам. 20 (4): 642–653. Дои:10.1111 / j.2153-3490.1968.tb00406.x.
- ^ https://pdfs.semanticscholar.org/edaa/8fc5e196791c821a5c81e987e2f5ca3c6aa5.pdf
- ^ Ян, Джин; Сун, Сяо; Гонг, Гуанхун (2016). «Среднее соотношение между дополнительными профилями для оценки искажений формы картографических проекций и сферических иерархических мозаик». Компьютеры и науки о Земле. 87: 41–55. Дои:10.1016 / j.cageo.2015.11.009.
- ^ «What3words: находите и делитесь очень точными местоположениями с помощью Карт Google с помощью всего 3 слов». 2013-07-02. Получено 8 июля 2014.
- ^ «Open Location Code - это библиотека для генерации коротких кодов, которые можно использовать как почтовые адреса для мест, где почтовые адреса не существуют: Google / open-location-code». 2019-02-18.
- ^ «Вычислительная геометрия и пространственное индексирование на сфере: Google / s2geometry». 2019-02-18.
внешние ссылки
- OGC DGGS Рабочая группа по стандартам
- Дискретные глобальные сети страница на факультете компьютерных наук Университета Южного Орегона
- BUGS климатическая модель страница по геодезическим сеткам
- Научно-исследовательский институт мировых сеточных квадратов страница на World Grid Squares

