WikiDer > Индикатриса Tissots - Википедия

Tissots indicatrix - Wikipedia

В Проекция Бермана с индикатрисами Тиссо

В Проекция Меркатора с индикатрисами Тиссо

В картография, а Индикатриса Тиссо (Индикатриса Tissot, Эллипс Тиссо, Эллипс Тиссо, эллипс искажения) (множественное число: «индикатрисы Тиссо») - математическое изобретение, представленное французским математиком Николя Огюст Тиссо в 1859 и 1871 гг., чтобы охарактеризовать локальные искажения, вызванные картографическая проекция. Это геометрия, которая является результатом проектирование а круг из бесконечно малый радиус из изогнутой геометрической модели, например земного шара, на карту. Тиссо доказал, что полученная диаграмма эллипс чьи оси указывают на два основные направления по которой масштаб максимален и минимален в данной точке карты.

Единая индикатриса описывает искажение в одной точке. Поскольку искажения различаются по карте, обычно индикатрисы Tissot размещаются по карте, чтобы проиллюстрировать пространственное изменение искажения. Общая схема размещает их на каждом пересечении отображаемых меридианов и параллелей. Эти схемы важны при изучении картографических проекций, как для иллюстрации искажения, так и для обеспечения основы для вычислений, которые точно отражают величину искажения в каждой точке.

Между индикатрисой Tissot и индикатором существует однозначное соответствие. метрический тензор преобразования координат проекции карты.^[1]

Описание

Теория Тиссо была разработана в контексте картографический анализ. Как правило, геометрическая модель представляет Землю и имеет форму сфера или же эллипсоид.

Индикатрисы Тиссо иллюстрируют линейные, угловые и площадные искажения карт:

Карта искажает расстояния (линейное искажение) везде, где отношение длин бесконечно короткой линии, проецируемой на поверхность проекции, и, как это было изначально на модели Земли, отклоняется от единицы. масштаб. Если проекция не конформный в рассматриваемой точке масштабный коэффициент изменяется в зависимости от направления вокруг точки.
Карта искажает углы везде, где углы, измеренные на модели Земли, не сохраняются в проекции. Это выражается эллипсом искажения, который не является кругом.
Карта искажает области там, где области, измеренные в модели Земли, не сохраняются в проекции. Это выражается эллипсами искажения, площадь которых меняется по карте.

На конформных картах, где каждая точка сохраняет углы, спроецированные из геометрической модели, индикатрисы Tissot - это все круги, размер которых варьируется в зависимости от местоположения, возможно, также с различной ориентацией (учитывая четыре круга квадранты разделен на меридианы и параллели). В равновеликие проекции, где пропорции площадей между объектами сохранены, индикатрисы Tissot имеют одинаковую площадь, хотя их форма и ориентация меняются в зависимости от местоположения. В произвольных проекциях площадь и форма на карте различаются.

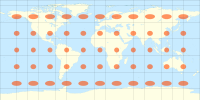
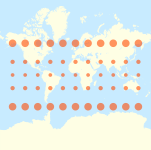
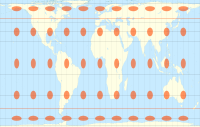
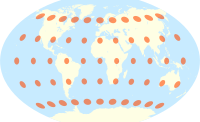
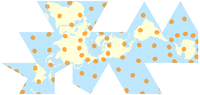
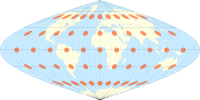
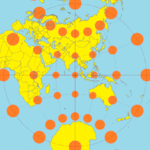
Карты мира, сравнивающие индикатрисы Tissot на некоторых общих проекциях
Равнопрямоугольная проекция Проекция Меркатора Проекция Галла – Петерса Проекция Моллвейде Проекция винкеля трипеля Азимутальная эквидистантная проекция Полная проекция Поперечная проекция Меркатора Цилиндрическая равновеликая проекция Ламберта Синусоидальная проекция Проекция Робинсона Стереографическая проекция

Математика

Индикатриса Тиссо

На соседнем изображении ABCD - это круг с единичной площадью, определенный в сферической или эллипсоидальной модели Земли, а A′B′C′D ′ - это индикатриса Tissot, которая получается в результате его проекции на плоскость. Сегмент OA преобразуется в OA ', а сегмент OB преобразуется в OB'. Линейный масштаб не сохраняется вдоль этих двух направлений, поскольку OA ′ не равен OA, а OB ′ не равен OB. Угол MOA в круге с единичной площадью преобразуется в угол M'OA 'в эллипсе искажения. Поскольку M′OA ′ ≠ MOA, мы знаем, что существует угловое искажение. Площадь круга ABCD по определению равна 1. Поскольку площадь эллипса A'B 'меньше 1, произошло искажение площади.

При работе с индикатрисой Tissot в игру вступают разные понятия радиуса. Первый - бесконечно малый радиус исходной окружности. Результирующий эллипс искажения также будет иметь бесконечно малый радиус, но по математике дифференциалы, отношения этих бесконечно малых значений конечны. Так, например, если результирующий эллипс искажения имеет такой же бесконечно малый размер, что и на сфере, то его радиус считается равным 1. Наконец, размер, который индикатрица рисуется для просмотра человеком на карте, является произвольным. Когда на карте рисуется массив индикатрис, все они масштабируются на одинаковую произвольную величину, чтобы их размеры были пропорционально правильными.

Нравиться M на схеме оси из О по параллели и по меридиану может претерпевать изменение длины и вращение при проецировании. В литературе принято представлять масштаб вдоль меридиана как час и масштабировать по параллели как k, для данной точки. Точно так же угол между меридианом и параллелью мог измениться с 90 ° на другое значение. В самом деле, если карта не конформна, все углы, кроме одного, ограниченного большая полуось и малая полуось эллипса могло измениться. Определенный угол изменится больше всего, и значение этого максимального изменения известно как угловая деформация, обозначаемая как θ ′. Как правило, то, какой это угол и как он ориентирован, не играет большой роли при анализе искажений. Значительна ценность изменения. Ценности час, k, и θ ′ можно вычислить следующим образом.^[2]^:24

{ displaystyle { begin {align} h & = { frac {1} {R}} { sqrt {{{ left ({ frac { partial x} { partial varphi}} right)} ^ {2}} + {{ left ({ frac { partial y} { partial varphi}} right)} ^ {2}}}} k & = { frac {1} {R cos varphi}} { sqrt {{{ left ({ frac { partial x} { partial lambda}} right)} ^ {2}} + {{ left ({ frac { partial y } { partial lambda}} right)} ^ {2}}}} sin theta '& = { frac {1} {R ^ {2} hk cos varphi}} left ( {{ frac { partial y} { partial varphi}} { frac { partial x} { partial lambda}} - { frac { partial x} { partial varphi}} { frac { partial y} { partial lambda}}} right) a '& = { sqrt {{h ^ {2}} + {k ^ {2}} + 2hk sin theta'}} b '& = { sqrt {{h ^ {2}} + {k ^ {2}} - 2hk sin theta'}} a & = { frac {a '+ b'} {2 }} b & = { frac {a'-b '} {2}} s & = hk sin theta' omega & = 2 arcsin left ({ frac {b '} { а '}} справа) конец {выровнено}}}

куда φ и λ широта и долгота, Икс и у проектируемые координаты, и р это радиус земного шара.

В результате а и б представляют максимальный и минимальный масштабные коэффициенты в точке, что аналогично большой и малой полуосям эллипса Tissot; s представляет собой величину инфляции или дефляции в области (также определяется как а ∙ б); и ω представляет собой максимальное угловое искажение в точке.

Для Проекция Меркатора, и любые другие конформный проекция час = k и θ ′ = 90 °, так что каждый эллипс вырождается в окружность радиуса час = k равный коэффициенту масштабирования в любом направлении в этой точке.

Для синусоидальная проекция, и любые другие равновеликий проекции большая полуось эллипса обратна малой полуоси, так что каждый эллипс имеет одинаковую площадь, даже если их эксцентриситет отличаться.

Для произвольных проекций ни форма, ни площадь эллипсов не связаны друг с другом в целом.^[3]

Альтернативный вывод для численного расчета

Другой способ понять и вывести индикатрису Тиссо - использовать дифференциальную геометрию поверхностей.^[4] Этот подход хорошо подходит для современных численных методов, поскольку параметры индикатрисы Тиссо могут быть вычислены с использованием разложение по сингулярным числам (СВД) и аппроксимация центральной разности.

Дифференциальное расстояние на эллипсоиде

Пусть 3D точка, ${ displaystyle { hat {X}}}$ , на эллипсоиде параметризовать как:

{ displaystyle { hat {X}} ( lambda, phi) = left [{ begin {matrix} N cos { lambda} cos { phi} - N (1-e ^ { 2}) sin { phi} N sin { lambda} cos { phi} end {matrix}} right]}

куда ${ Displaystyle ( лямбда, фи)}$ - долгота и широта соответственно, и ${ displaystyle N}$ является функцией экваториального радиуса, ${ displaystyle R}$ , и эксцентриситет, ${ displaystyle e}$ :

{ displaystyle N = { frac {R} { sqrt {1-e ^ {2} sin ^ {2} ( phi)}}}}

Элемент расстояния на сфере, ${ displaystyle ds}$ определяется первая фундаментальная форма:

{ displaystyle ds ^ {2} = { begin {bmatrix} d lambda & d phi end {bmatrix}} { begin {bmatrix} E&F F&G end {bmatrix}} { begin {bmatrix} d lambda d phi end {bmatrix}}}

коэффициенты которого определяются как:

{ displaystyle { begin {align} & E = { frac { partial { hat {X}}} { partial lambda}} { boldsymbol { cdot}} { frac { partial { hat { X}}} { partial lambda}} & F = { frac { partial { hat {X}}} { partial lambda}} { boldsymbol { cdot}} { frac { partial { hat {X}}} { partial phi}} & G = { frac { partial { hat {X}}} { partial phi}} { boldsymbol { cdot}} { frac { partial { hat {X}}} { partial phi}} конец {выровненный}}}

Вычисление необходимых производных дает:

{ displaystyle { frac { partial { hat {X}}} { partial lambda}} = left [{ begin {matrix} -N sin { lambda} cos { phi} 0 N cos { lambda} cos { phi} end {matrix}} right] qquad qquad { frac { partial { hat {X}}} { partial phi}} = left [{ begin {matrix} -M cos { lambda} sin { phi} - M cos { phi} M sin { lambda} sin { phi} конец {матрица}} right]}

куда ${ displaystyle M}$ является функцией экваториального радиуса, ${ displaystyle R}$ , и эксцентриситет эллипсоида, ${ displaystyle e}$ :

{ Displaystyle M = { гидроразрыва {R (1-e ^ {2})} {(1-e ^ {2} sin ^ {2} ( phi)) ^ { frac {3} {2} }}}}

Подстановка этих значений в первую фундаментальную форму дает формулу для элементарного расстояния на эллипсоиде:

{ displaystyle ds ^ {2} = left (N cos { phi} right) ^ {2} d lambda ^ {2} + M ^ {2} d phi ^ {2}}

Этот результат связывает меру расстояния на поверхности эллипсоида как функцию сферической системы координат.

Преобразование элемента расстояния

Напомним, что цель индикатрисы Тиссо - показать, как расстояния на сфере меняются при сопоставлении с плоской поверхностью. В частности, желаемое соотношение - это преобразование ${ displaystyle { mathcal {T}}}$ который связывает дифференциальное расстояние вдоль оснований сферической системы координат с дифференциальным расстоянием вдоль оснований декартовой системы координат на плоской карте. Это можно выразить соотношением:

{ displaystyle { begin {bmatrix} dx dy end {bmatrix}} = { mathcal {T}} { begin {bmatrix} ds ( lambda, 0) ds (0, phi) конец {bmatrix}}}

куда ${ displaystyle ds ( lambda, 0)}$ и ${ displaystyle ds (0, phi)}$ представляют собой вычисление ${ displaystyle ds}$ по продольной и широтной осям соответственно. Расчет ${ displaystyle ds ( lambda, 0)}$ и ${ displaystyle ds (0, phi)}$ можно выполнить непосредственно из приведенного выше уравнения, что дает:

{ Displaystyle { begin {align} & ds ( lambda, 0) = N cos ( phi) d lambda & ds (0, phi) = Md phi end {align}}}

Для целей этого вычисления полезно выразить эту взаимосвязь как матричную операцию:

{ displaystyle { begin {bmatrix} d lambda d phi end {bmatrix}} = K { begin {bmatrix} ds ( lambda, 0) ds (0, phi) end { bmatrix}}, qquad K = { begin {bmatrix} { frac {1} {N cos { phi}}} & 0 0 & { frac {1} {M}} end {bmatrix}} }

Теперь, чтобы связать расстояния на поверхности эллипсоида с расстояниями на плоскости, нам нужно связать системы координат. Из цепного правила мы можем написать:

{ displaystyle { begin {bmatrix} dx dy end {bmatrix}} = J { begin {bmatrix} d lambda d phi end {bmatrix}}}

где J - Матрица якобиана:

{ Displaystyle J = { begin {bmatrix} { frac { partial x} { partial lambda}} & { frac { partial x} { partial phi}} { frac { partial y} { partial lambda}} и { frac { partial y} { partial phi}} end {bmatrix}}}

Подставляя матричное выражение для ${ displaystyle d lambda}$ и ${ displaystyle d phi}$ дает определение преобразования ${ displaystyle { mathcal {T}}}$ в виде индикатрисы:

{ displaystyle { begin {bmatrix} dx dy end {bmatrix}} = JK { begin {bmatrix} ds ( lambda, 0) ds (0, phi) end {bmatrix}}}

{ displaystyle { mathcal {T}} = JK}

Это преобразование ${ displaystyle { mathcal {T}}}$ инкапсулирует отображение поверхности эллипсоида на плоскость. Выражаясь в этой форме, СВД может использоваться для выделения важных компонентов локальной трансформации.

Численные вычисления и SVD

Чтобы извлечь желаемую информацию об искажении в любом заданном месте сферической системы координат, значения ${ displaystyle K}$ можно вычислить напрямую. Якобиан, ${ displaystyle J}$ , может быть вычислен аналитически из самой функции отображения, но часто проще численно аппроксимировать значения в любом месте на карте, используя центральные различия. Как только эти значения вычислены, SVD может применяться к каждой матрице преобразования для извлечения информации о локальных искажениях. Помните, что, поскольку искажение является локальным, каждое место на карте будет иметь собственное преобразование.

Напомним определение СВД:

{ Displaystyle mathrm {SVD} ({ mathcal {T}}) = U Lambda V ^ {T}}

Это разложение преобразования, ${ displaystyle { mathcal {T}}}$ , во вращение в исходной области (т.е. поверхности эллипсоида), ${ Displaystyle V ^ {T}}$ , масштабирование по основанию, ${ displaystyle Lambda}$ , и последующее второе вращение, ${ displaystyle U}$ . Для понимания искажения первое вращение не имеет значения, поскольку оно вращает оси окружности, но не влияет на окончательную ориентацию эллипса. Следующая операция, представленная диагональной матрицей сингулярных значений, масштабирует круг по его осям, деформируя его в эллипс. Таким образом, сингулярные значения представляют собой масштабные коэффициенты по осям эллипса. Первое сингулярное значение представляет собой большую полуось, ${ displaystyle a}$ , а второй обеспечивает малую полуось, ${ displaystyle b}$ , которые являются коэффициентами масштабирования искажений по направлению. Масштабное искажение можно вычислить как площадь эллипса, ${ displaystyle ab}$ , или, что то же самое, определителем ${ displaystyle { mathcal {T}}}$ . Наконец, ориентация эллипса, ${ displaystyle theta}$ , можно извлечь из первого столбца ${ displaystyle U}$ в качестве: