WikiDer > Естественная проекция Земли
Natural Earth projection
 | Эта статья отсутствует информация об искажении, программном обеспечении и полиноме. (Февраль 2017 г.) |
Естественная проекция Земли с Индикатриса Тиссо деформации
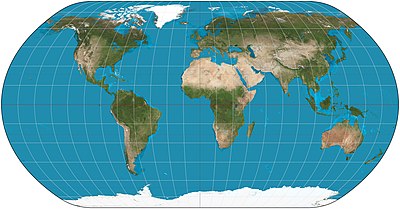
В естественная проекция Земли это псевдоцилиндрический картографическая проекция разработано Том Паттерсон и введен в 2012 году. конформный ни равновеликий.
Он был разработан в Flex Projector, специализированном программном приложении, которое предлагает графический подход для создания новых проекций.[1][2]
Определение
Естественная Земля определяется следующими формулами:
- ,
куда
- Икс, у - декартовы координаты;
- λ долгота от центрального меридиана;
- φ это широта;
- л(φ) - длина параллели по широте φ;
- d(φ) - расстояние параллели от экватора на широте φ.
л(φ) и d(φ) задаются как полиномы, первоначально из интерполяция следующих значений в Flex Projector[3]:
| φ (градусы) | л(φ) | d(φ) |
|---|---|---|
| 0 | 1.0000 | 0.0000 |
| 5 | 0.9988 | 0.0620 |
| 10 | 0.9953 | 0.1240 |
| 15 | 0.9894 | 0.1860 |
| 20 | 0.9811 | 0.2480 |
| 25 | 0.9703 | 0.3100 |
| 30 | 0.9570 | 0.3720 |
| 35 | 0.9409 | 0.4340 |
| 40 | 0.9222 | 0.4958 |
| 45 | 0.9006 | 0.5571 |
| 50 | 0.8763 | 0.6176 |
| 55 | 0.8492 | 0.6769 |
| 60 | 0.8196 | 0.7346 |
| 65 | 0.7874 | 0.7903 |
| 70 | 0.7525 | 0.8435 |
| 75 | 0.7160 | 0.8936 |
| 80 | 0.6754 | 0.9394 |
| 85 | 0.6270 | 0.9761 |
| 90 | 0.5630 | 1.0000 |
Значения для южного полушария рассчитываются путем изменения знака соответствующих значений для северного полушария.
Смотрите также
Рекомендации
- ^ Шаврич, Боян; Дженни, Бернхард; Паттерсон, Том; Петрович, Душан; Хурни, Лоренц (17 февраля 2012 г.). «Полиномиальное уравнение для естественной проекции Земли» (PDF). Государственный университет Орегона. Архивировано из оригинал (PDF) на 2016-03-03. Получено 24 января, 2020.
- ^ Дженни, Бернхард; Паттерсон, Том; Хурни, Лоренц (2008). «Flex Projector - Интерактивная программа для проектирования карт мира». Картографические перспективы. Получено 24 января, 2020.
- ^ "Естественная проекция Земли: Дом". www.shadedrelief.com. Архивировано из оригинал на 2012-04-07. Получено 2017-02-12.
Первоначально он был разработан в Flex Projector с использованием графических методов, а теперь существует как полиномиальная версия.